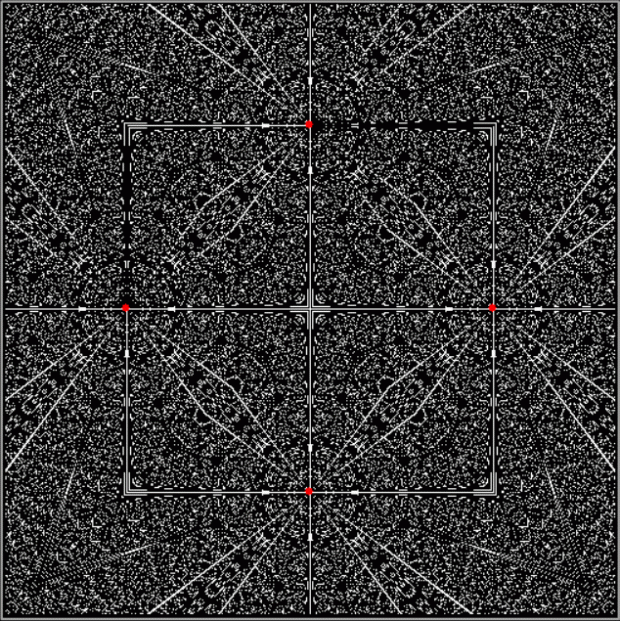
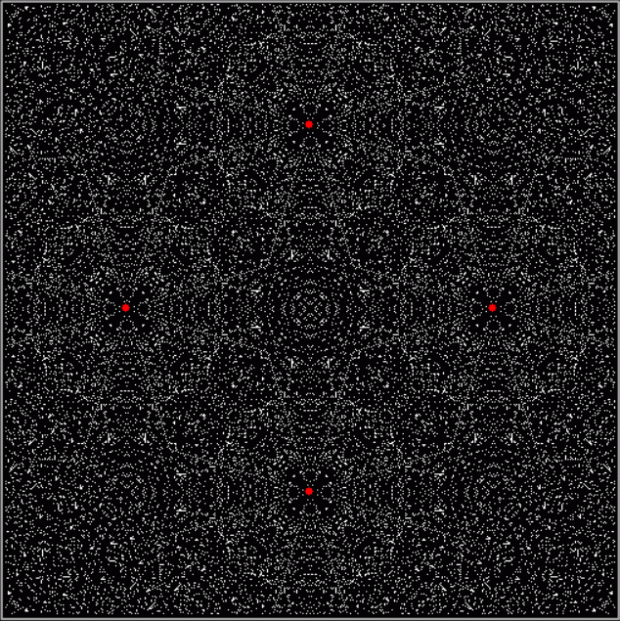
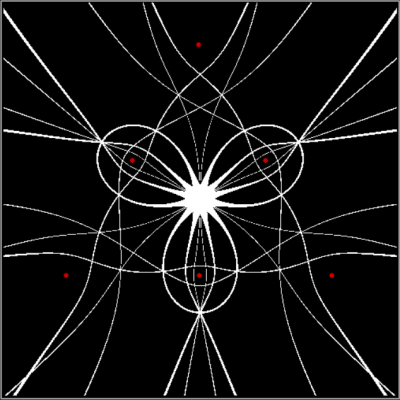
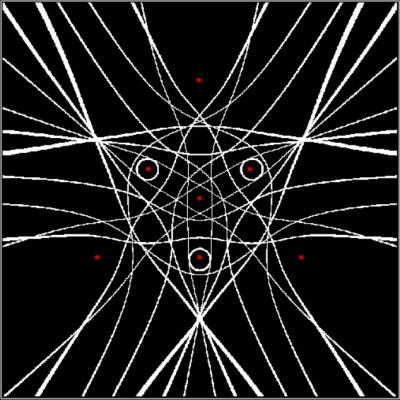
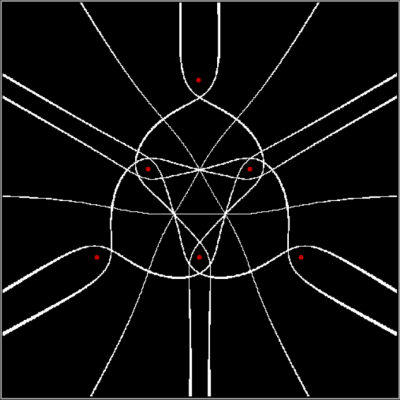
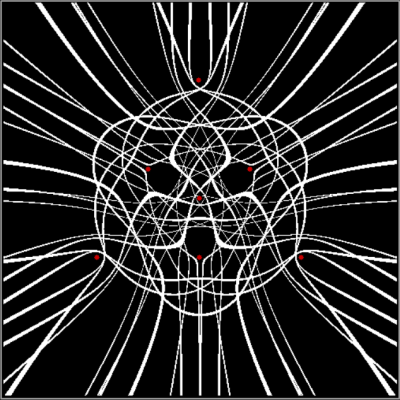
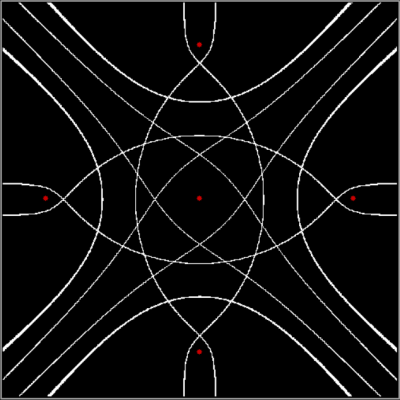
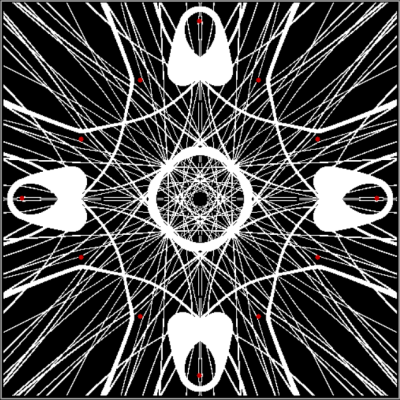
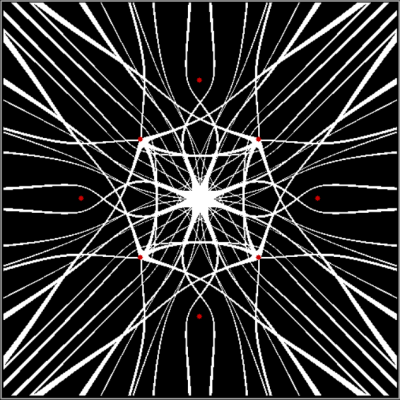
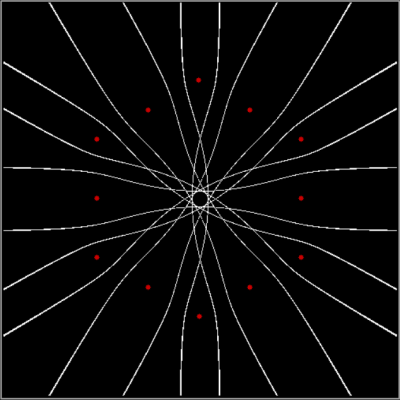
As I’ve pre-previously pointed out, there are an infinite number of points in the plane. And in part of the plane. So you have to pare points to create interesting shapes. One way of paring points is by comparing them. After you’ve compared them, you can sort them. For example, you can compare the distance from (x,y) to the four vertices of a square. Then you can sort the distances from nearest to furthest. Then you can mark (x,y) if the distance to, say, the nearest vertice from (x,y) is evenly divisible by 2 when measured in pixels or some other unit. When you do that, you might get an image like this (depending on the hardware and software you use):

Distance to nearest vertex is evenly divisible by 2, i.e. d mod 2 = 0 for v1 (vertices marked in red)

---

Or you can mark (x,y) if the distance to the nearest vertex is a triangular number:

is_triangular(d) for v1

---

Or a square number:

is_square(d) for v1

---

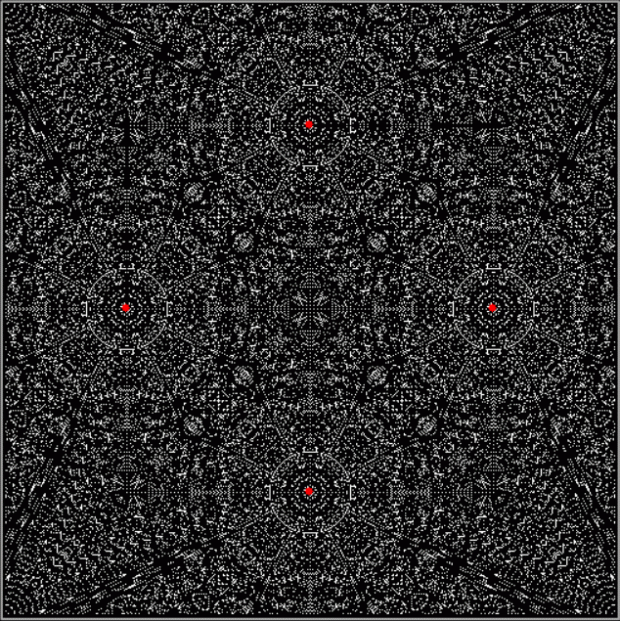
Or you can test the distance to the second-nearest vertex:

d mod 2 = 0 for v2

---

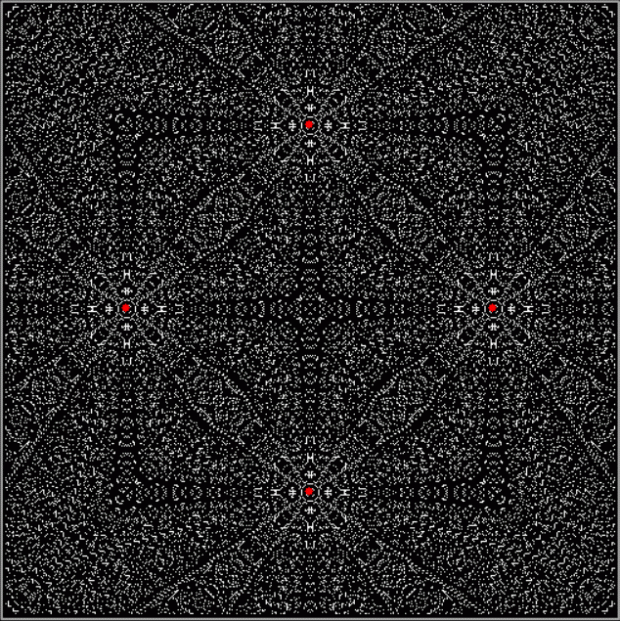
And the third-nearest (or second-furthest) vertex:

d mod 2 = 0 for v3

---

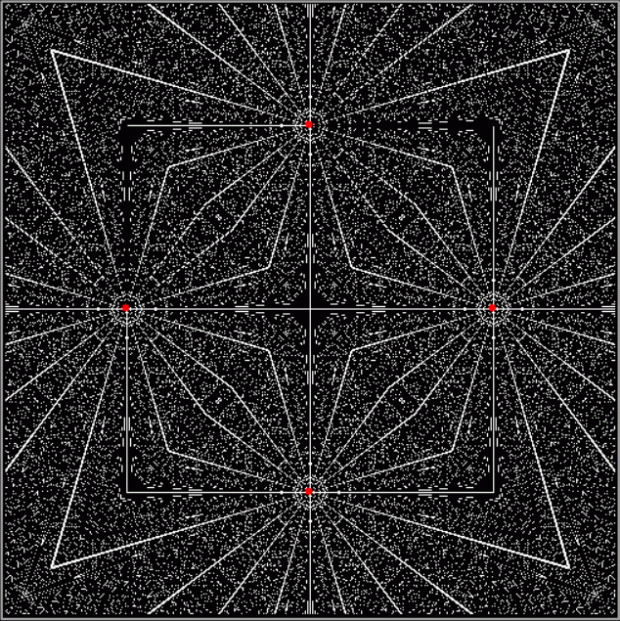
And furthest vertex:

d mod 2 = 0 for v4

---

Now try expanding or contracting the square:

d mod 2 = 0 for v1 on square * 2

---

d mod 2 = 0 for v1 on square * 3

---

d mod 2 = 0 for v1 on square * 0.5

---

d mod 2 = 0 for v1 on square * 1.5

---

d mod 2 = 0 for v1 on square * 5

---

d mod 2 = 0 for v1 on square * 20

---

d mod 2 = 0 for v1 on square * 100

---

Finally, here are some more mandala-like images created by using various d mod m on an expanded square (the images should be horizontally and vertically mirror-symmetrical, but my software introduced artefacts):

d mod 2 = 0 for v1 on square * 200
(open in separate window for better detail)

---

d mod 3 = 0 for v1 on square * 200

---

d mod 4 = 0 for v1 on square * 200

---

d mod 5 = 0 for v1 on square * 200

---

d mod 6 = 0 for v1 on square * 200

---

d mod 7 = 0 for p1 on square * 200

---

d mod 8 = 0 for p1 on square * 200

---

d mod 9 = 0 for p1 on square * 200

---

d mod 2..9 = 0 for p1 on square * 200 (animated at EZgif)

---

Post-Performative Post-Scriptum…

The title of this incendiary intervention is a paronomasia on “Sorted for E’s and Wizz”, a song offa of 1995 album Different Class by Sheffield Brit-popsters Pulp rebelliously referencing counter-cultural consumption of psychoactive drugs ecstasy and amphetamine. My program sorted distances, i.e. d’s, but not wizz, therefore it sorted d’s and-not wizz. In Boolean logic, nand means “and-not” (roughly speaking).

---

Previously Pre-Posted (Please Peruse)…

• Points Pared — an earlier look at points and polygons