Category Archives: Pi

Pyramidic Palindromes

by in Base Behavior, Integer sequences, π, Mathematics, Palindromic numbers, Pi, Powers, Squares and tagged , , , , , , , , , , , | Leave a comment

As I’ve said before on Overlord of the Über-Feral: squares are boring. As I’ve shown before on Overlord of the Über-Feral: squares are not so boring after all.

Take A000330 at the Online Encyclopedia of Integer Sequences:

1, 5, 14, 30, 55, 91, 140, 204, 285, 385, 506, 650, 819, 1015, 1240, 1496, 1785, 2109, 2470, 2870, 3311, 3795, 4324, 4900, 5525, 6201, 6930, 7714, 8555, 9455, 10416, 11440, 12529, 13685, 14910, 16206, 17575, 19019, 20540, 22140, 23821, 25585, 27434, 29370… — A000330 at OEIS

The sequence shows the square pyramidal numbers, formed by summing the squares of integers:

• 1 = 1^2
• 5 = 1^2 + 2^2 = 1 + 4
• 14 = 1^2 + 2^2 + 3^2 = 1 + 4 + 9
• 30 = 1^2 + 2^2 + 3^2 + 4^2 = 1 + 4 + 9 + 16

[…]

You can see the pyramidality of the square pyramidals when you pile up oranges or cannonballs:

Square pyramid of 91 cannonballs at Rye Castle, East Sussex (Wikipedia)

I looked for palindromes in the square pyramidals. These are the only ones I could find:

1 (k=1)
5 (k=2)
55 (k=5)
1992991 (k=181)

The only ones in base 10, that is. When I looked in base 9 = 3^2, I got a burst of pyramidic palindromes like this:

1 (k=1)
5 (k=2)
33 (k=4) = 30 in base 10 (k=4)
111 (k=6) = 91 in b10 (k=6)
122221 (k=66) = 73810 in b10 (k=60)
123333321 (k=666) = 54406261 in b10 (k=546)
123444444321 (k=6,666) = 39710600020 in b10 (k=4920)
123455555554321 (k=66,666) = 28952950120831 in b10 (k=44286)
123456666666654321 (k=666,666) = 21107018371978630 in b10 (k=398580)
123456777777777654321 (k=6,666,666) = 15387042129569911801 in b10 (k=3587226)
123456788888888887654321 (k=66,666,666) = 11217155797104231969640 in b10 (k=32285040)

The palindromic pattern from 6[…]6 ends with 66,666,666, because 8 is the highest digit in base 9. When you look at the 666,666,666th square pyramidal in base 9, you’ll find it’s not a perfect palindrome:

123456801111111111087654321 (k=666,666,666) = 8177306744945450299267171 in b10 (k=290565366)

But the pattern of pyramidic palindromes is good while it lasts. I can’t find any other base yielding a pattern like that. And base 9 yields another burst of pyramidic palindromes in a related sequence, A000537 at the OEIS:

1, 9, 36, 100, 225, 441, 784, 1296, 2025, 3025, 4356, 6084, 8281, 11025, 14400, 18496, 23409, 29241, 36100, 44100, 53361, 64009, 76176, 90000, 105625, 123201, 142884, 164836, 189225, 216225, 246016, 278784, 314721, 354025, 396900, 443556, 494209, 549081… — A000537 at OEIS

The sequence is what you might call the cubic pyramidal numbers, that is, the sum of the cubes of integers:

• 1 = 1^2
• 9 = 1^2 + 2^3 = 1 + 8
• 36 = 1^3 + 2^3 + 3^3 = 1 + 8 + 27
• 100 = 1^3 + 2^3 + 3^3 + 4^3 = 1 + 8 + 27 + 64

[…]

I looked for palindromes there in base 9:

1 (k=1) = 1 (k=1)
121 (k=4) = 100 in base 10 (k=4)
12321 (k=14) = 8281 (k=13)
1234321 (k=44) = 672400 (k=40)
123454321 (k=144) = 54479161 (k=121)
12345654321 (k=444) = 4412944900 (k=364)
1234567654321 (k=1444) = 357449732641 (k=1093)
123456787654321 (k=4444) = 28953439105600 (k=3280)
102012022050220210201 (k=137227) = 12460125198224404009 (k=84022)

But while palindromes are fun, they’re not usually mathematically significant. However, this result using the square pyrmidals is certainly significant:

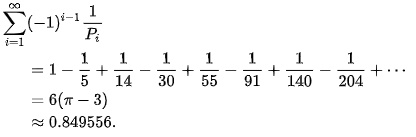
Previously Pre-Posted…

More posts about how squares aren’t so boring after all:

• Curvous Energy
• Back to Drac #1
• Back to Drac #2
• Square’s Flair

Pi in the Bi

by in Binary numbers, Mathematics, Pi and tagged , , , , , , , , , , , , | Leave a comment

Binary is beautiful — both simple and subtle. What could be simpler than using only two digits to count with?


0, 1, 10, 11, 100, 101, 110, 111, 1000, 1001, 1010, 1011, 1100, 1101, 1110, 1111, 10000, 10001, 10010, 10011, 10100, 10101, 10110, 10111, 11000, 11001, 11010, 11011, 11100, 11101, 11110, 11111, 100000, 100001, 100010, 100011, 100100, 100101, 100110, 100111, 101000, 101001, 101010, 101011, 101100, 101101, 101110, 101111, 110000, 110001, 110010, 110011, 110100, 110101, 110110, 110111, 111000, 111001, 111010, 111011, 111100, 111101, 111110, 111111, 1000000...

But the simple patterns in the two digits of binary involve two of the most important numbers in mathematics: π and e (aka Euler’s number):


π = 3.141592653589793238462643383...
e = 2.718281828459045235360287471...

It’s easy to write π and e in binary:


π = 11.00100 10000 11111 10110 10101 00010...
e = 10.10110 11111 10000 10101 00010 11000...

But how do π and e appear in the patterns of binary 1 and 0? Well, suppose you use the digits of binary to generate the sums of distinct integers. For example, here are the sums of distinct integers you can generate with three digits of binary, if you count the digits from right to left (so the rightmost digit is 1, the the next-to-rightmost digit is 2, the next-to-leftmost digit is 3, and the leftmost digit is 4):


0000 → 0*4 + 0*3 + 0*2 + 0*1 = 0
0001 → 0*4 + 0*3 + 0*2 + 1*1 = 1*1 = 1
0010 → 0*4 + 0*3 + 1*2 + 0*1 = 1*2 = 2
0011 → 0*4 + 0*3 + 1*2 + 1*1 = 1*2 + 1*1 = 3
0100 → 1*3 = 3
0101 → 1*3 + 1*1 = 4
0110 → 3 + 2 = 5
0111 → 3 + 2 + 1 = 6
1000 → 4
1001 → 4 + 1 = 5
1010 → 4 + 2 = 6
1011 → 4 + 2 + 1 = 7
1100 → 4 + 3 = 7
1101 → 4 + 3 + 1 = 8
1110 → 4 + 3 + 2 = 9
1111 → 4 + 3 + 2 + 1 = 10

There are 16 sums (16 = 2^4) generating 11 integers, 0 to 10. But some integers involve more than one sum:


3 = 2 + 1 ← 0011
3 = 3 ← 0100

4 = 3 + 1 ← 0101
4 = 4 ← 1000

5 = 3 + 2 ← 0110
5 = 4 + 1 ← 1001

6 = 3 + 2 + 1 ← 0111
6 = 4 + 2 ← 1010

7 = 4 + 2 + 1 ← 1011
7 = 4 + 3 ← 1100

Note the symmetry of the sums: the binary number 0011, yielding 3, is the mirror of 1100, yielding 7; the binary number 0100, yielding 3 again, is the mirror of 1011, yielding 7 again. In each pair of mirror-sums, the two numbers, 3 and 7, are related by the formula 10-3 = 7 and 10-7 = 3. This also applies to 4 and 6, where 10-4 = 6 and 10-6 = 4, and to 5, which is its own mirror (because 10-5 = 5). Now, try mapping the number of distinct sums for 0 to 10 as a graph:

Graph for distinct sums of the integers 0 to 4

The graph show how 0, 1 and 2 have one sum each, 3, 4, 5, 6 and 7 have two sums each, and 8, 9 and 10 have one sum each. Now look at the graph for sums derived from three digits of binary:

Graph for distinct sums of the integers 0 to 3

The single taller line of the seven lines represents the two sums of 3, because three digits of binary yield only one sum for 0, 1, 2, 4, 5 and 6:


000 → 0
001 → 1
010 → 2
011 → 2 + 1 = 3
100 → 3
101 → 3 + 1 = 4
110 → 3 + 2 = 5
111 → 3 + 2 + 1 = 6

Next, look at graphs for sums derived from one to sixteen binary digits and note how the symmetry of the lines begins to create a beautiful curve (the y axis is normalized, so that the highest number of sums reaches the same height in each graph):

Graph for sums from 1 binary digit

Graph for sums from 2 binary digits

Graph for sums from 3 binary digits

Graph for sums from 4 binary digits

Graph for sums from 5 binary digits

Graph for sums from 6 binary digits

Graph for sums from 7 binary digits

Graph for sums from 8 binary digits

Graph for sums from 9 binary digits

Graph for sums from 10 binary digits

Graph for sums from 11 binary digits

Graph for sums from 12 binary digits

Graph for sums from 13 binary digits

Graph for sums from 14 binary digits

Graph for sums from 15 binary digits

Graph for sums from 16 binary digits

Graphs for 1 to 16 binary digits (animated)

You may recognize the shape emerging above as the bell curve, whose formula is this:

Formula for the normal distribution or bell curve (image from ThoughtCo)

And that’s how you can find pi in the bi, or π in the binary digits of 0, 1, 10, 11, 100, 101, 110, 111, 1000, 1001, 1010, 1011, 1100, 1101…

(And how you find e too, as promised above.)

Post-Performative Post-Scriptum

I asked this question above: What could be simpler than using only two digits? Well, using only one digit is simpler still:


1, 11, 111, 1111, 11111, 111111, 1111111, 11111111, 111111111, 1111111111...

But I don’t see an easy way to find π and e in numbers like that.

La Formule de François

by in √2, Infinity, Irrational numbers, π, Mathematics, Pi, Square root of 2, Square Roots and tagged , , , , , , | Leave a comment

Here is a beautiful and astonishingly simple formula for π created by the French mathematician François Viète (1540-1603):

• 2 / π = √2/2 * √(2 + √2)/2 * √(2 + √(2 + √2))/2…

I can remember testing the formula on a scientific calculator that allowed simple programming. As I pressed the = key and the results began to home in on π, I felt as though I was watching a tall and elegant temple emerge through swirling mist.

Pi and By

by in √2, Base Behavior, Binary numbers, Integer sequences, Irrational numbers, π, Mathematics, Pi, Square root of 2 and tagged , , , , , , , , , , , , , , , , , , , | Leave a comment

Here’s √2 in base 2:

√2 = 1.01101010000010011110... (base=2)

And in base 3:

√2 = 1.10201122122200121221... (base=3)

And in bases 4, 5, 6, 7, 8, 9 and 10:

√2 = 1.12220021321212133303... (b=4)
√2 = 1.20134202041300003420... (b=5)
√2 = 1.22524531420552332143... (b=6)
√2 = 1.26203454521123261061... (b=7)
√2 = 1.32404746317716746220... (b=8)
√2 = 1.36485805578615303608... (b=9)
√2 = 1.41421356237309504880... (b=10)

And here’s π in the same bases:

π = 11.00100100001111110110... (b=2)
π = 10.01021101222201021100... (b=3)
π = 03.02100333122220202011... (b=4)
π = 03.03232214303343241124... (b=5)
π = 03.05033005141512410523... (b=6)
π = 03.06636514320361341102... (b=7)
π = 03.11037552421026430215... (b=8)
π = 03.12418812407442788645... (b=9)
π = 03.14159265358979323846... (b=10)

Mathematicians know that in all standard bases, the digits of √2 and π go on for ever, without falling into any regular pattern. These numbers aren’t merely irrational but transcedental. But are they also normal? That is, in each base b, do the digits 0 to [b-1] occur with the same frequency 1/b? (In general, a sequence of length l will occur in a normal number with frequency 1/(b^l).) In base 2, are there as many 1s as 0s in the digits of √2 and π? In base 3, are there as many 2s as 1s and 0s? And so on.

It’s a simple question, but so far it’s proved impossible to answer. Another question starts very simple but quickly gets very difficult. Here are the answers so far at the Online Encyclopedia of Integer Sequences (OEIS):

2, 572, 8410815, 59609420837337474 – A049364

The sequence is defined as the “Smallest number that is digitally balanced in all bases 2, 3, … n”. In base 2, the number 2 is 10, which has one 1 and one 0. In bases 2 and 3, 572 = 1000111100 and 210012, respectively. 1000111100 has five 1s and five 0s; 210012 has two 2s, two 1s and two 0s. Here are the numbers of A049364 in the necessary bases:

10 (n=2)
1000111100, 210012 (n=572)
100000000101011010111111, 120211022110200, 200011122333 (n=8410815)
11010011110001100111001111010010010001101011100110000010, 101201112000102222102011202221201100, 3103301213033102101223212002, 1000001111222333324244344 (n=59609420837337474)

But what number, a(6), satisfies the definition for bases 2, 3, 4, 5 and 6? According to the notes at the OEIS, a(6) > 5^434. That means finding a(6) is way beyond the power of present-day computers. But I assume a quantum computer could crack it. And maybe someone will come up with a short-cut or even an algorithm that supplies a(b) for any base b. Either way, I think we’ll get there, π and by.

Lette’s Roll

by in Geometry, π, Mathematics, Pi and tagged , , , , , , , , , , , , , , , , , , , | Leave a comment

A roulette is a little wheel or little roller, but it’s much more than a game in a casino. It can also be one of a family of curves created by tracing the path of a point on a rotating circle. Suppose a circle rolls around another circle of the same size. This is the resultant roulette:
roulette1

roulette1static
The shape is called a cardioid, because it looks like a heart (kardia in Greek). Now here’s a circle with radius r rolling around a circle with radius 2r:
roulette2

roulette2static

That shape is a nephroid, because it looks like a kidney (nephros in Greek).

This is a circle with radius r rolling around a circle with radius 3r:
roulette3

roulette3static
And this is r and 4r:
roulette4

roulette4static
The shapes above might be called outer roulettes. But what if a circle rolls inside another circle? Here’s an inner roulette whose radius is three-fifths (0.6) x the radius of its rollee:
roulette5

roulette5static
The same roulette appears inverted when the inner circle has a radius two-fifths (0.4) x the radius of the rollee:
roulette5a
But what happens when the circle rolling “inside” is larger than the rollee? That is, when the rolling circle is effectively swinging around the rollee, like a bunch of keys being twirled on an index finger? If the rolling radius is 1.5 times larger, the roulette looks like this:
roulette6
If the rolling radius is 2 times larger, the roulette looks like this:
roulette2over

Here are more outer, inner and over-sized roulettes:

roulette_outer

roulette_inner

roulette_over

And you can have circles rolling inside circles inside circles:

roulette7

roulette0616

roulette0616all

And here’s another circle-in-a-circle in a circle:

roulette07c015c

He Say, He Sigh, He Sow #20

by in Binary numbers, Geometry, π, Mathematics, Pi, Quotations and tagged , , , , , , , , , , , , , , , , , , , , , | 6 Comments

“In 1997, Fabrice Bellard announced that the trillionth digit of π, in binary notation, is 1.” — Ian Stewart, The Great Mathematical Problems (2013).