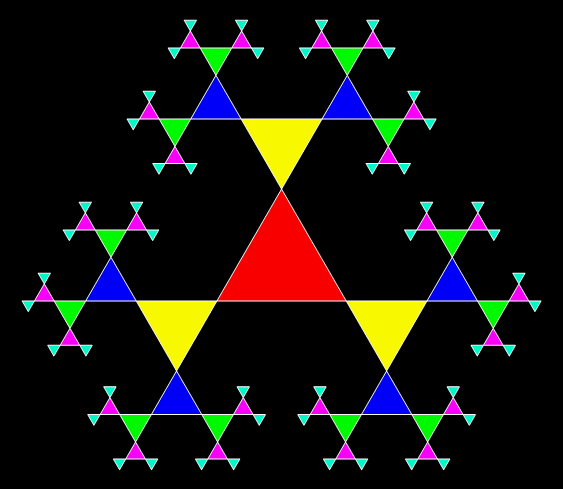
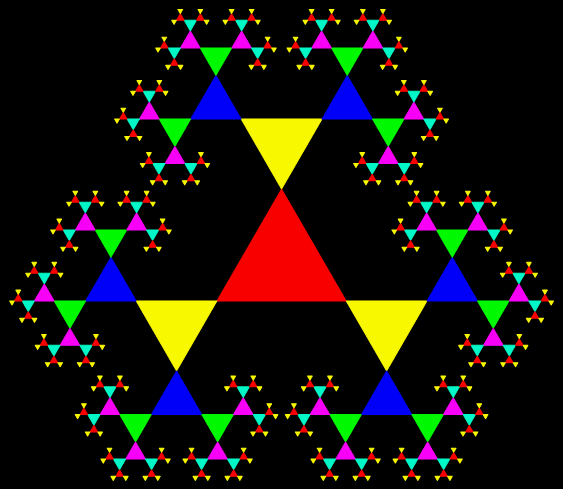
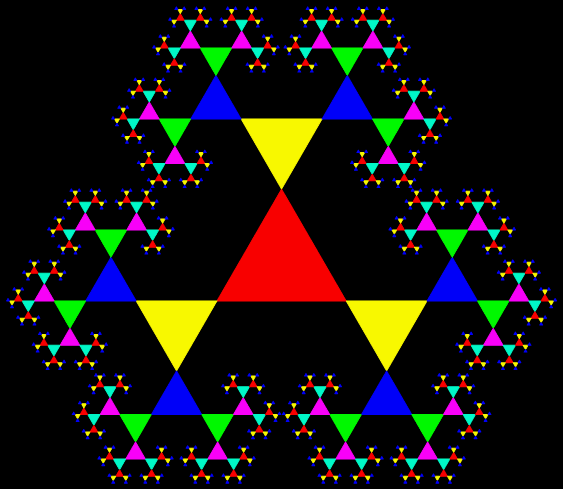
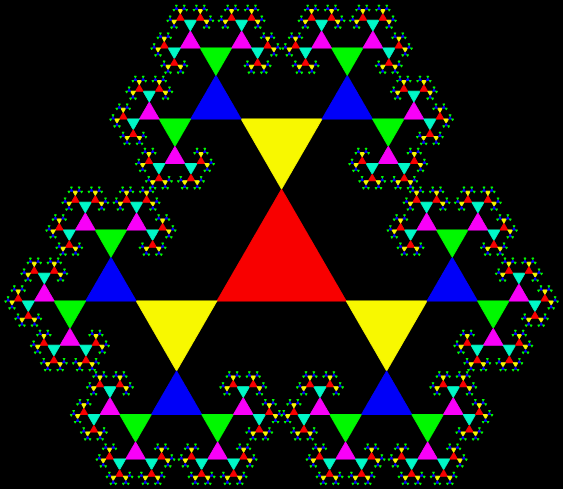
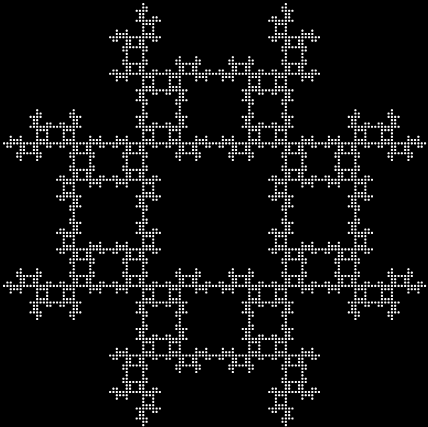Suppose you trace all possible routes followed by a point inside a triangle jumping halfway towards one or another of the three vertices of the triangle. If you mark each jump, you get a famous geometrical shape called the Sierpiński triangle (or Sierpiński sieve).
Sierpiński triangle found by tracing all possible routes for a point jumping halfway towards the vertices of a triangle
The Sierpiński triangle is a fractal, because it contains copies of itself at smaller and smaller scales. Now try the same thing with a square. If you trace all possible routes followed by a point inside a square jumping halfway towards one or another of the four vertices of the square, you don’t get an obvious fractal. Instead, the interior of the square fills steadily (and will eventually be completely solid):
Routes of a point jumping halfway towards vertices of a square
Try a variant. If the point is banned from jumping towards the same vertex twice or more in a row, the routes trace out a fractal that looks like this:
Ban on choosing same vertex twice or more in a row
If the point is banned from jumping towards the vertex one place anti-clockwise of the vertex it’s just jumped towards, you get a fractal like this:
Ban on jumping towards vertex one place anti-clockwise of previously chosen vertex
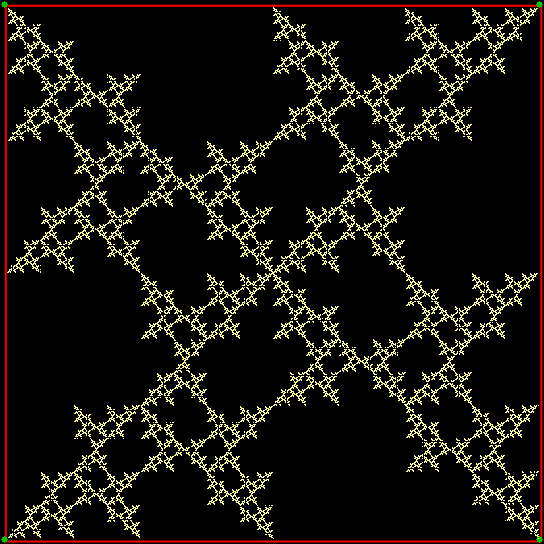
And if the point can’t jump towards two places clockwise or anti-clockwise of the currently chosen vertex, this fractal appears (called a T-square fractal):
Ban on jumping towards the vertex diagonally opposite of the previously chosen vertex
That ban is equivalent to banning the point from jumping from the vertex diagonally opposite to the vertex it’s just jumped towards. Finally, here’s the fractal created when you ban the point from jumping towards the vertex one place clockwise of the vertex it’s just jumped towards:
Ban on jumping towards vertex one place clockwise of previously chosen vertex
As you can see, the fractal is a mirror-image of the one-place-anti-clockwise-ban fractal.
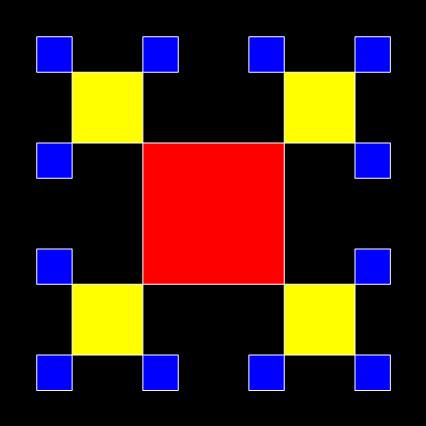
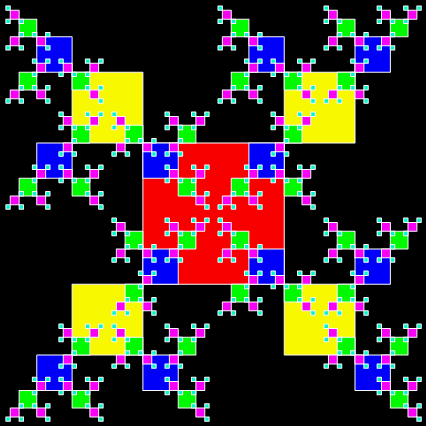
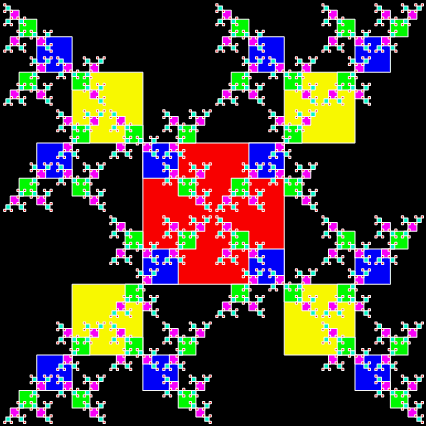
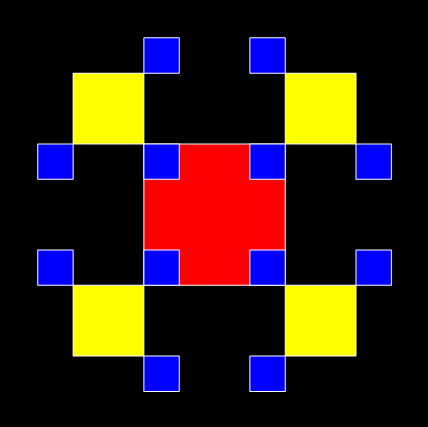
I discovered the ban-construction of those fractals more than twenty years ago. Then I found that I was re-discovering the same fractals when I looked at what first seemed like completely different ways of constructing fractals. There are lots of different routes to the same result. I’ve recently discovered yet another route. Let’s try what seems like an entirely different way of constructing fractals. Take a square and erect four new half-sized squares, sq1, sq2, sq3, sq4, on each corner. Then erect three more quarter-sized squares on the outward facing corners of sq1, sq2, sq3 and sq4. Carry on doing that and see what happens at the end when you remove all the previous stages of construction:
Animation of the new construction
Animation in black-and-white
It’s the T-square fractal again. Now try rotating the squares you add at stage 3 and see what happens (the rotation means that two new squares are added on adjacent outward-facing corners and one new square on the inward-facing corner):
Animation of the construction
It’s the one-place-clockwise-ban fractal again. Now try rotating the squares two places, so that two new squares are added on diagonally opposite outward-facing corners and one new square on the inward-facing corner:
Animation of the construction
It’s the same-vertex-ban fractal again. Finally, rotate squares one place more:
Animation of the construction
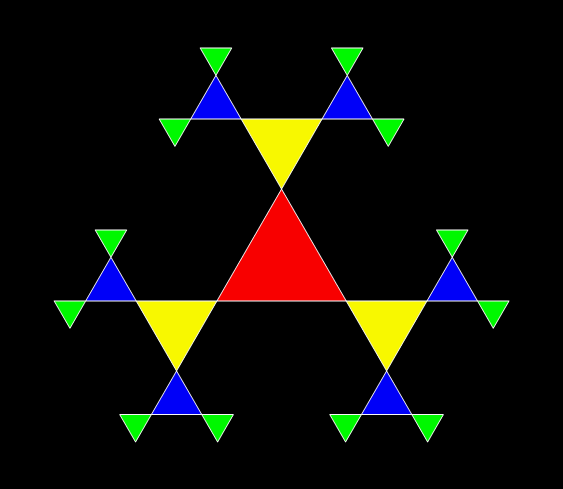
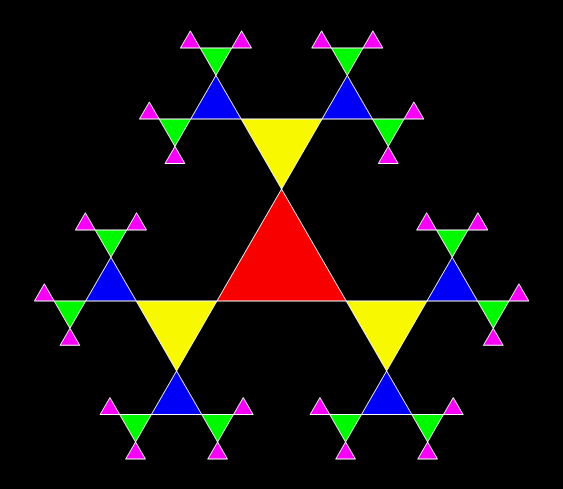
It’s the one-place-clockwise-ban fractal again. And this method isn’t confined to squares. Here’s what happens when you add 5/8th-sized triangles to the corners of triangles:
Animation of the construction
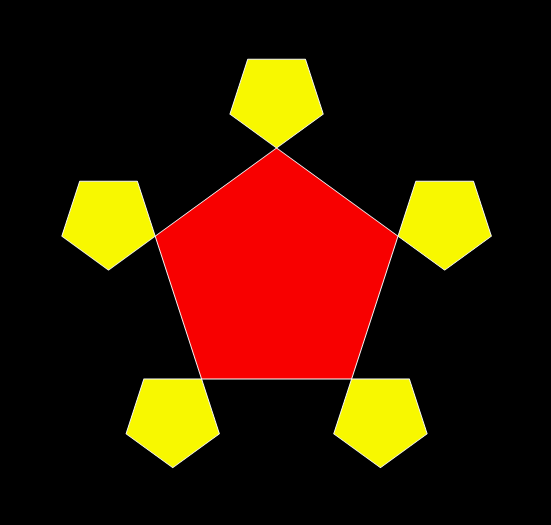
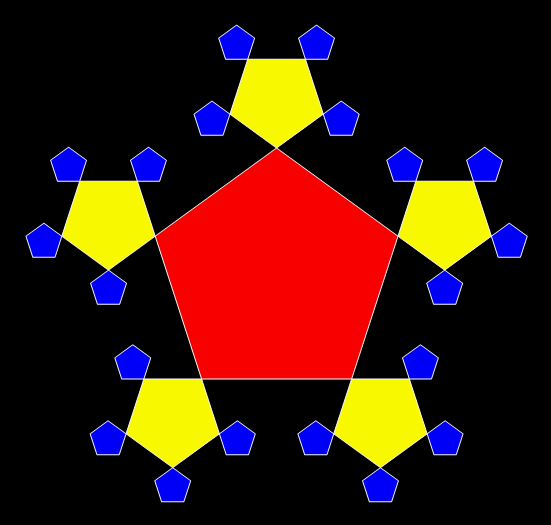
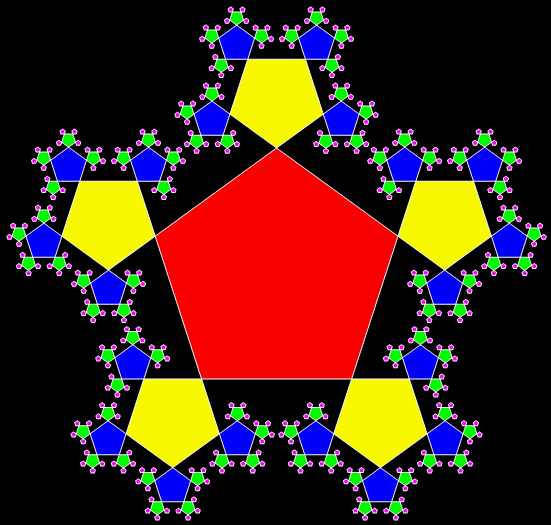
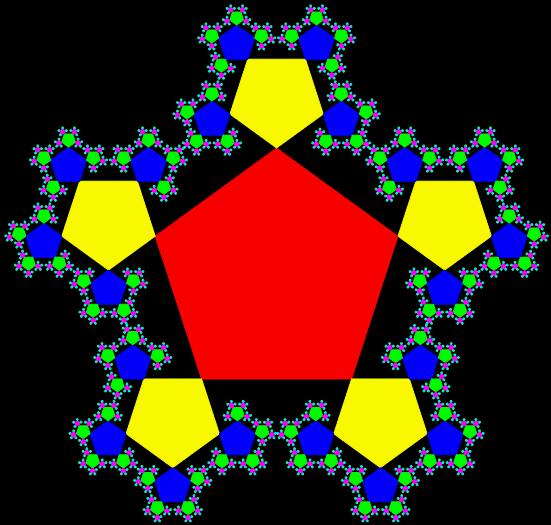
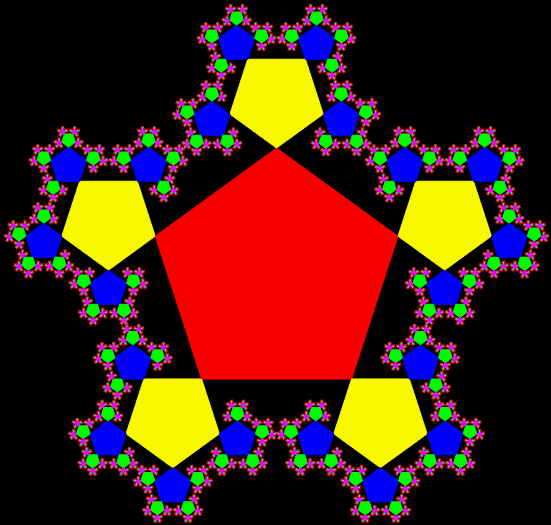
And here’s what happens when you add 5/13th-sized pentagons to the corners of pentagons:
Animation of the construction
Finally, here’s a variant on that pentagonal fractal (adding two rather than four pentagons at stage 3 and higher):
Animation of the construction
Previously pre-posted (please peruse):
• Square Routes
• Square Routes Revisited
• Square Routes Re-Revisited
• Square Routes Re-Re-Revisited
• Square Routes Re-Re-Re-Revisited
• Square Routes Re-Re-Re-Re-Revisited
• Square Routes Re-Re-Re-Re-Re-Revisited