One of my favourite integer sequences has the simple formula n(i) = n(i-1) + digitsum(n(i-1)). If it’s seeded with 1, its first few terms go like this:
n(1) = 1
n(2) = n(1) + digitsum(n(1)) = 1 + digitsum(1) = 2
n(3) = 2 + digitsum(2) = 4
n(4) = 4 + digitsum(4) = 8
n(5) = 8 + digitsum(8) = 16
n(6) = 16 + digitsum(16) = 16 + 1+6 = 16 + 7 = 23
n(7) = 23 + digitsum(23) = 23 + 2+3 = 23 + 5 = 28
n(8) = 28 + digitsum(28) = 28 + 2+8 = 28 + 10 = 38
As a sequence, it looks like this:
1, 2, 4, 8, 16, 23, 28, 38, 49, 62, 70, 77, 91, 101, 103, 107, 115, 122, 127, 137, 148, 161, 169, 185, 199, 218, 229, 242, 250, 257, 271, 281, 292, 305, 313, 320, 325, 335, 346, 359, 376, 392, 406, 416, 427, 440, 448, 464, 478, 497, 517, 530, 538, 554, 568, 587, 607, 620, 628, 644, 658, 677, 697, 719, 736, 752, 766, 785, 805, 818, 835, 851, 865, 884, 904, 917, 934, 950, 964, 983, 1003…
Given a number at random, is there a quick way to say whether it appears in the sequence seeded with 1? Not that I know, with one exception. If the number is divisible by 3, it doesn’t appear, at least in base 10. In base 2, that rule doesn’t apply:
n(1) = 1
n(2) = 1 + digitsum(1) = 10 = 1 + 1 = 2
n(3) = 10 + digitsum(10) = 10 + 1 = 11 = 2 + 1 = 3
n(4) = 11 + digitsum(11) = 11 + 1+1 = 101 = 3 + 2 = 5
n(5) = 101 + digitsum(101) = 101 + 1+0+1 = 111 = 5 + 2 = 7
n(6) = 111 + digitsum(111) = 111 + 11 = 1010 = 7 + 3 = 10
n(7) = 1010 + digitsum(1010) = 1010 + 10 = 1100 = 10 + 2 = 12
n(8) = 1100 + digitsum(1100) = 1100 + 10 = 1110 = 12 + 2 = 14
1, 2, 3, 5, 7, 10, 12, 14, 17, 19, 22, 25, 28, 31, 36, 38, 41, 44, 47, 52, 55, 60, 64, 65, 67, 70, 73, 76, 79, 84, 87, 92, 96, 98, 101, 105, 109, 114, 118, 123, 129, 131, 134, 137, 140, 143, 148, 151, 156, 160, 162, 165, 169, 173, 178, 182, 187, 193, 196, 199, 204, 208, 211, 216, 220, 225, 229, 234, 239, 246, 252, 258, 260, 262, 265, 268, 271, 276, 279, 284, 288, 290, 293, 297, 301, 306, 310, 315, 321, 324, 327, 332, 336, 339, 344, 348, 353, 357, 362, 367, 374…
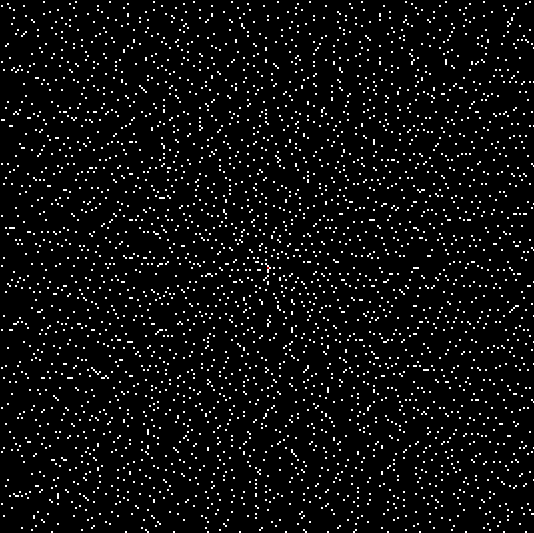
What patterns are there in these sequences? It’s easier to check when they’re represented graphically, so I converted them into patterns à la the Ulam spiral, where n is represented as a dot on a spiral of integers. This is the spiral for base 10:
And these are the spirals for bases 2 and 3:
Base 2
Base 3
These sequences look fairly random to me: there are no obvious patterns in the jumps from n(i) to n(i+1), i.e. in the values for digitsum(n(i)). Now try the spirals for bases 9 and 33:
Base 9
Base 33
Patterns have appeared: there is some regularity in the jumps. You can see these regularities more clearly if you represent digitsum(n(i)) as a graph, with n(i) on the x axis and digitsum(n(i)) on the y axis. If the graph starts with n(i) = 1 on the lower left and proceeds left-right, left-right up the screen, it looks like this in base 10:
Base 10 (click to enlarge)
Here are bases 2 and 3:
Base 2
Base 3
The jumps seem fairly random. Now try bases 9, 13, 16, 17, 25, 33 and 49:
Base 9
Base 13
Base 16
Base 17
Base 25
Base 33
Base 49
In some bases, the formula n(i) = n(i-1) + digitsum(n(i-1)) generates mild randomness. In others, it generates strong regularity, like waves rolling ashore under a steady wind. I don’t understand why, but regularity seems to occur in bases that are one more than a power of 2 and also in some bases that are primes or squares.
Elsewhere other-posted: