Category Archives: Chaos Game

Scout the Routes

by in Chaos Game, Fractals, Geometry, Mathematics, Squares and tagged , , , , , , , , | Leave a comment

Triangles? Yes. Squares? No. If you scout the routes with a triangle, you get a beautiful fractal. If you scout the routes with a square, you don’t. Here’s what you get with a triangle:

A Sierpiński triangle

But how do you scout the routes? (That phrase works best in the American dialects where “scout” rhymes with “route”.) Simple: you mark the final positions reached when a point traces all possible ways of jumping, say, eight times 1/2-way towards the vertices of a polygon. Here’s an animation of a point scouting the routes of eight jumps towards the vertices of a triangle (it starts each time at the center):

Creating a Sierpiński triangle by scouting the routes (animated at Ezgif)

If you scout the routes with a square, you don’t get a fractal. Instead, the interior of the square fills evenly (and boringly) with the end-points of the routes:

Scouting the routes with a square (animated at Ezgif)

But you can create fractals with a square if you out routes as you scout routes. That is, if you exclude some routes and don’t mark their end-points. One way to do this is to compare the proposed next jump-vertex (vertex-jumped-towards) with the previous jump-vertex. For example, if the proposed jump-vertex, jv[t], is the same as the previous jump-vertex, jv[t-1], you don’t jump towards jv[t] or you jump towards it in a different way. The test is jv[t] = jv[t-1] + vi. If vi = 0 and you jump towards the clockwise neighbor of jv when the test is true, you get a fractal looking like this:

vi = 0, action = jv → jv + 1

Here’s the fractal if you jump towards the clockwise-neighbor-but-one when the test is true:

vi = 0, action = jv + 2

Now try varying the vi of the jv[t-1] + vi:

vi = 2, action = jv + 2

vi = 2, action = jv + 1

vi = 3, action = jv + 1

Or what about jumping in a different way towards jv when the test is true? If you jump 2/3 of the way rather 1/2, you get his fractal:

vi = 2, action = jump 2/3

And if you jump 4/3 of the way (i.e., you overshoot the vertex jv), you get this fractal:

vi = 0, action = jump 4/3rds to vertex

vi = 0, jump 4/3 (guide-square removed)

vi = 2, jump 4/3rds (guide-square removed)

And in this fractal the point jumps 2/3 of the way to the center of the square when the test is true:

vi = 2, action = jump 2/3rds of way to center of square

But why apply only one test to jv[1] and use only when one alternative jump? If jv[t] = jv[t-1] + 1 or jv[t] = jv[t-1] + 3, jv[t] becomes jv[t]+1 or jv[t]+3, respectively, you get this fractal:

vi = 1, jv + 1; vi = 3, jv + 3

Here are more fractals created by single and double tests:

vi = 1, jv + 1

vi = 0, jump 2/3

vi = 0, jump towards center 2/3rds

vi = 1, jump-center 2/3

vi = 2, jump 1/3; vi = 3, jump 1/1 (i.e, 1)

vi = 0, jv + 2; vi = 2, jump-center 1/2

vi = 0, jv + 2; vi = 2, jump-center 2/3

vi = 0, jv + 2; vi = 2, jump-center 4/3

vi = 0, jv + 1; vi = 2, jump 2/3

vi = 0, jv + 2; vi = 2, jump 2/3

vi = 0, jump 4/3; vi = 2, jv + 2

vi = 0, jump 2/3; vi = 2, jv + 1

vi = 0, jump 4/3; vi = 1, jv + 2

vi = 0, jump 2/3; vi = 2, jump 1/3

vi =0, jump 1/3; vi = 2, jump 2/3

vi = 0, jump 0/1 (i.e, 0); vi = 2, jump 1/3

Game of Throwns

by in Chaos Game, Fractals, Geometry, Mathematics, Squares, Triangles and tagged , , , , , , , , , , , , | Leave a comment

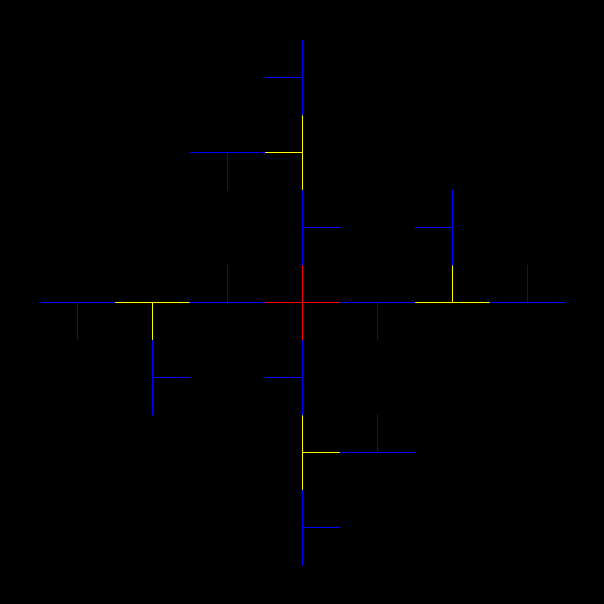
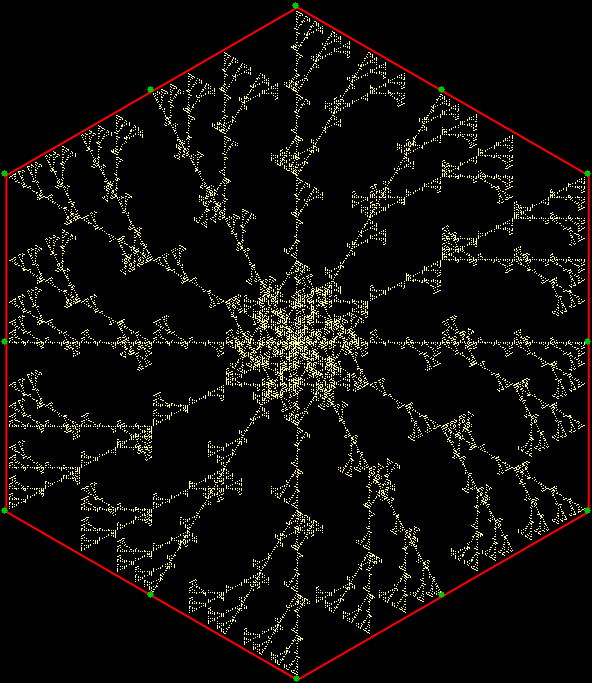
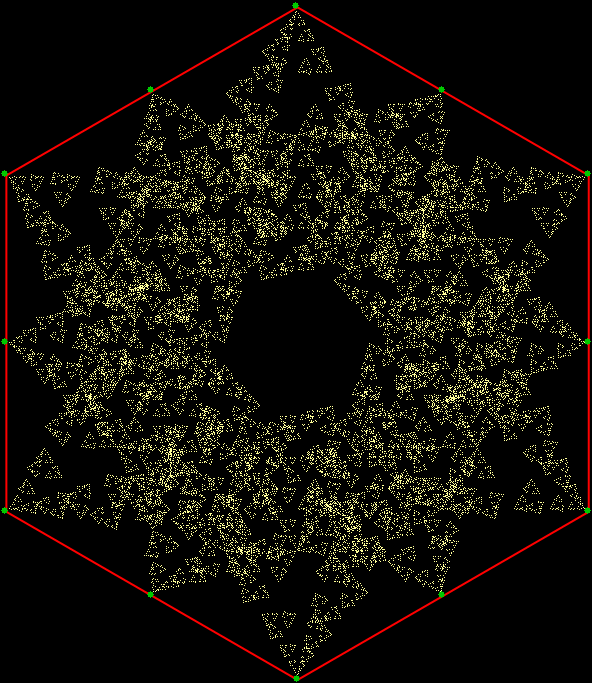
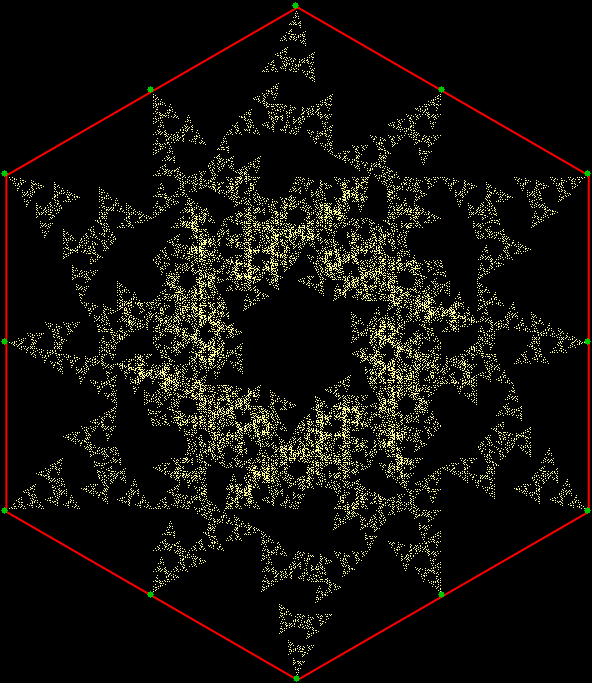
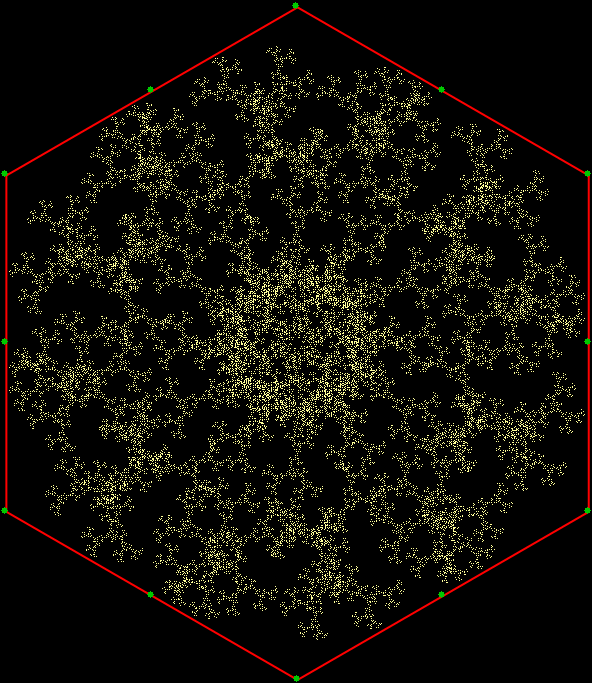
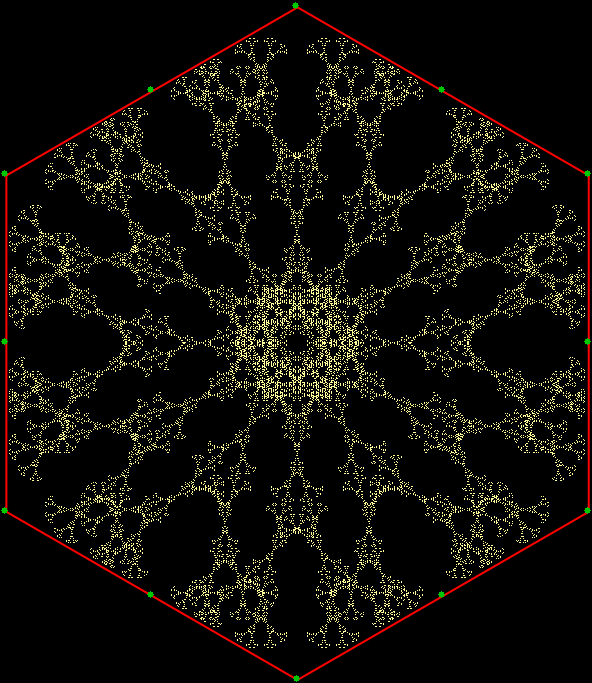
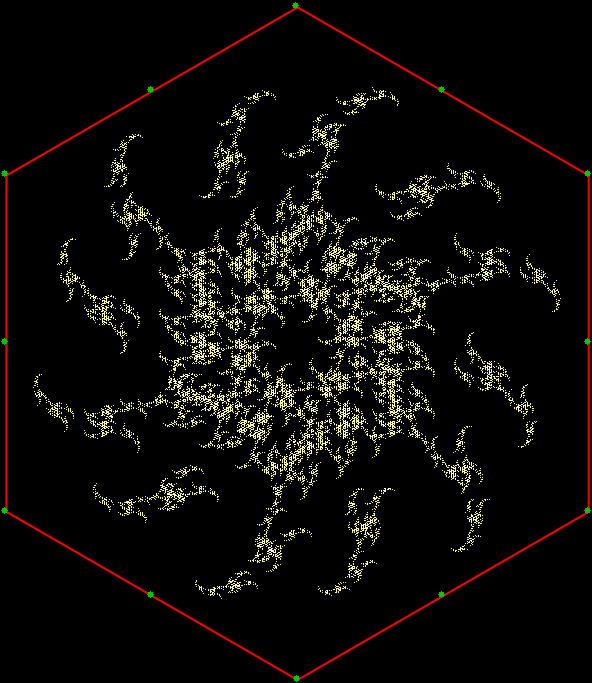
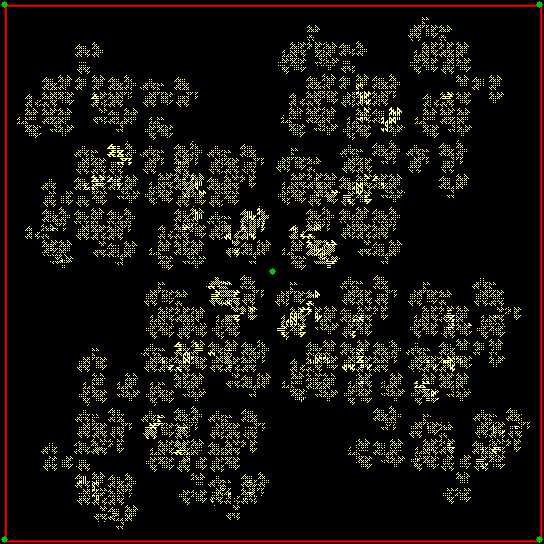In “Scaffscapes”, I looked at these three fractals and described how they were in a sense the same fractal, even though they looked very different:

Fractal #1

Fractal #2

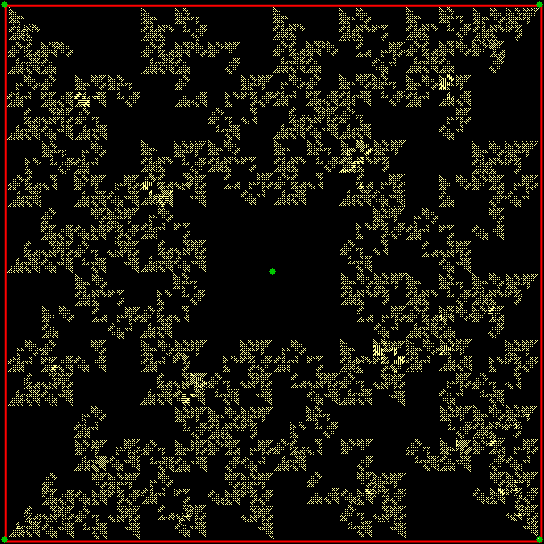
Fractal #3

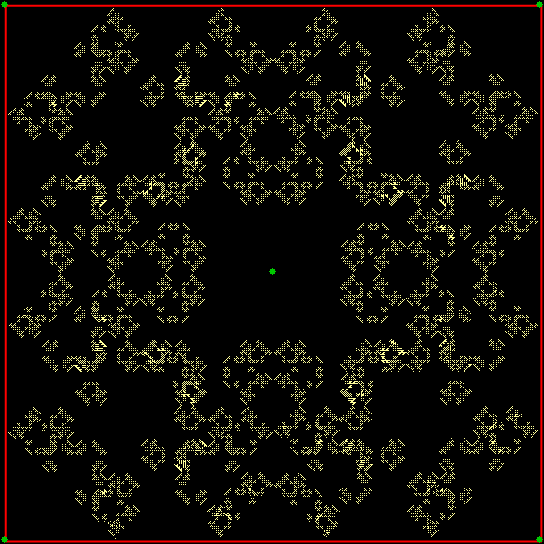
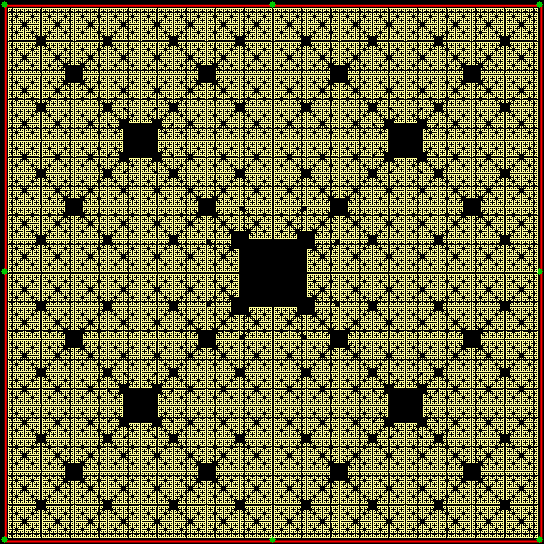
But even if they are all the same in some mathematical sense, their different appearances matter in an aesthetic sense. Fractal #1 is unattractive and seems uninteresting:

Fractal #1, unattractive, uninteresting and unnamed

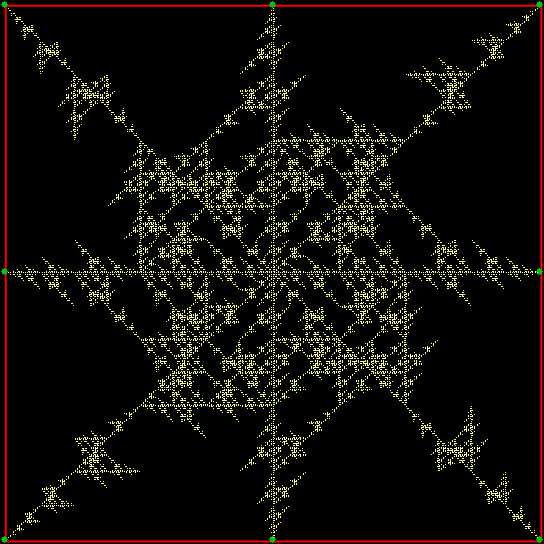
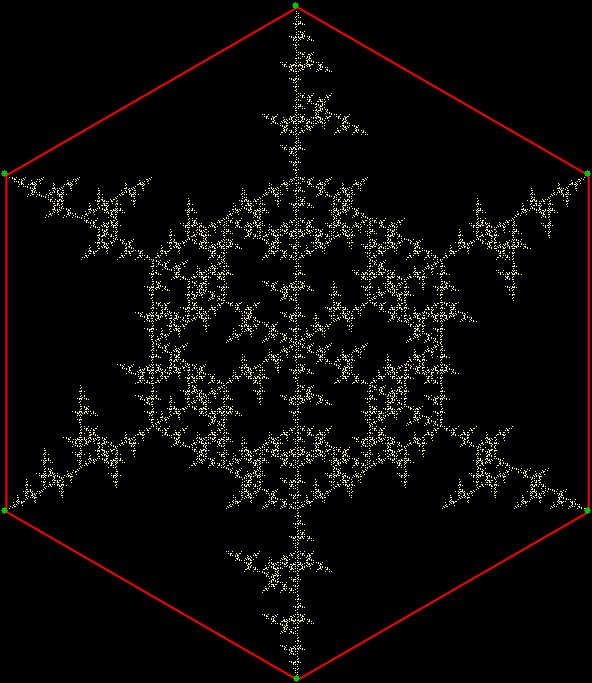
Fractal #3 is attractive and interesting. That’s part of why mathematicians have given it a name, the T-square fractal:

Fractal #3 — the T-square fractal

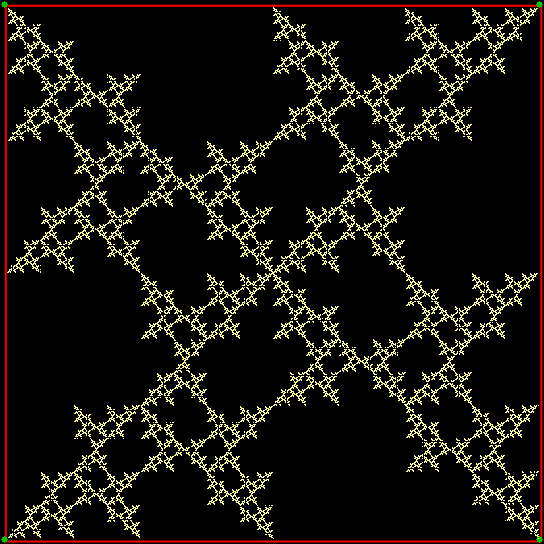
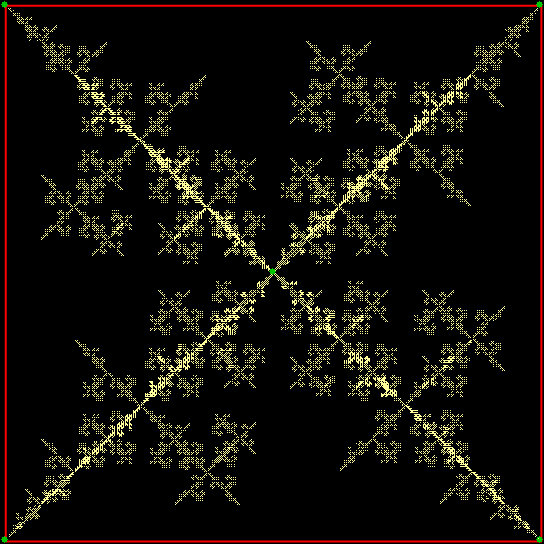
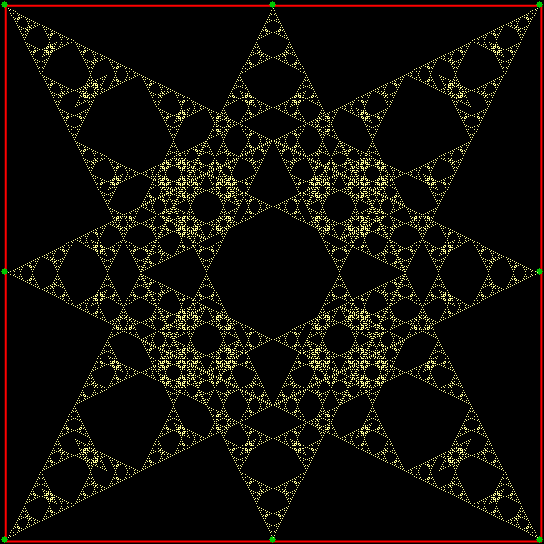
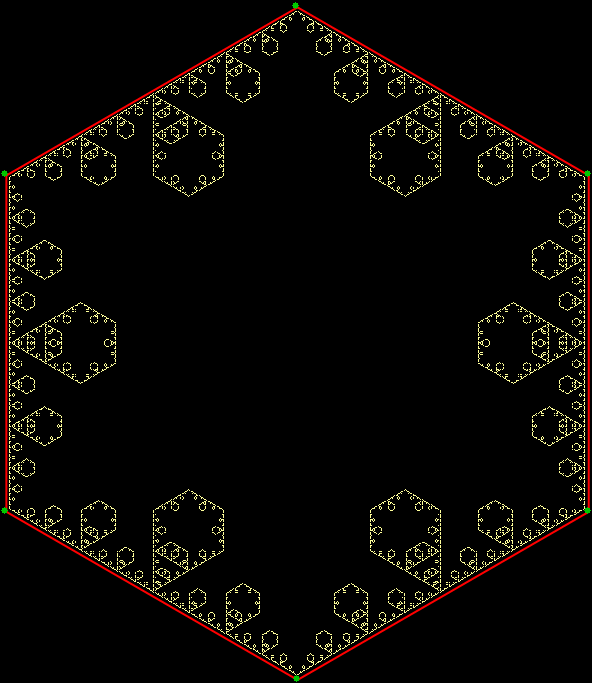
But fractal #2, although it’s attractive and interesting, doesn’t have a name. It reminds me of a ninja throwing-star or shuriken, so I’ve decided to call it the throwing-star fractal or ninja-star fractal:

Fractal #2, the throwing-star fractal

A ninja throwing-star or shuriken

This is one way to construct a throwing-star fractal:

Throwing-star fractal, stage 1

Throwing-star fractal, #2

Throwing-star fractal, #3

Throwing-star fractal, #4

Throwing-star fractal, #5

Throwing-star fractal, #6

Throwing-star fractal, #7

Throwing-star fractal, #8

Throwing-star fractal, #9

Throwing-star fractal, #10

Throwing-star fractal, #11

Throwing-star fractal (animated)

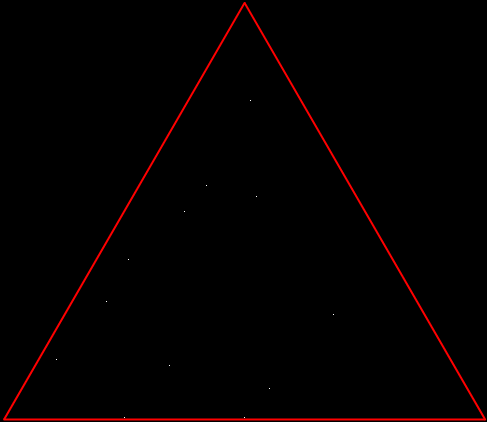
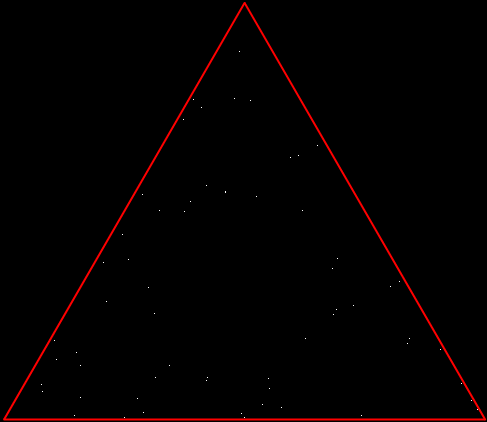
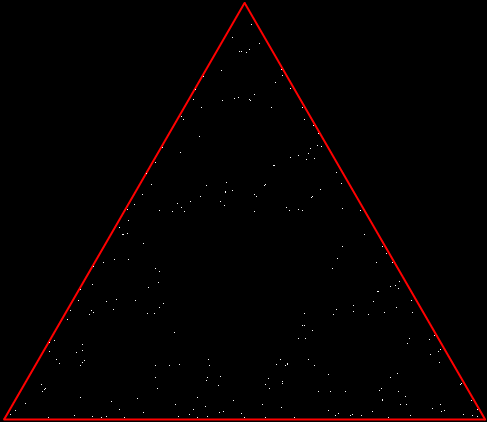
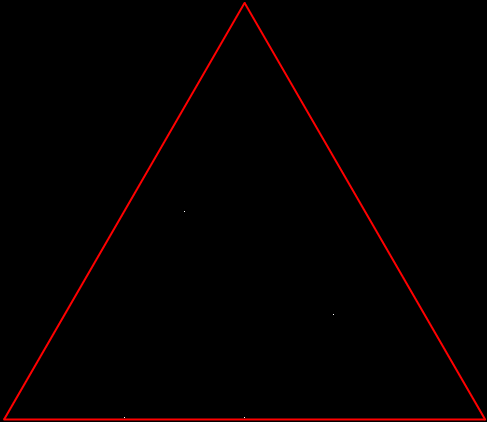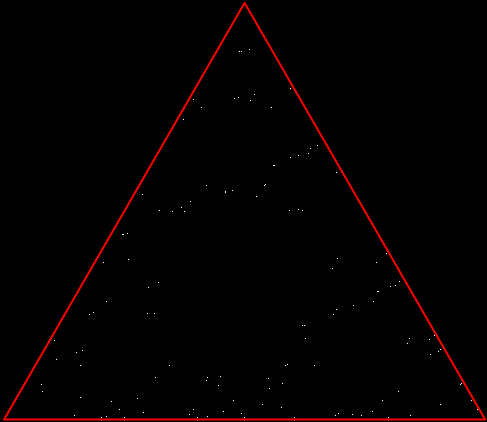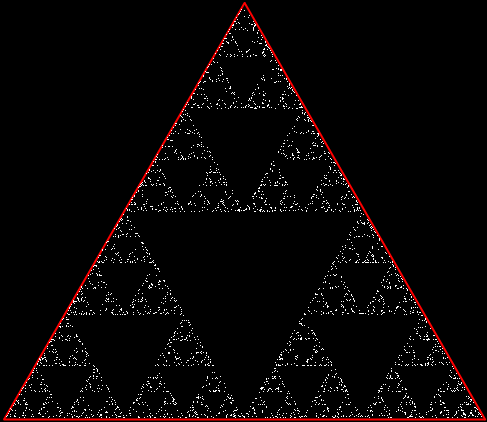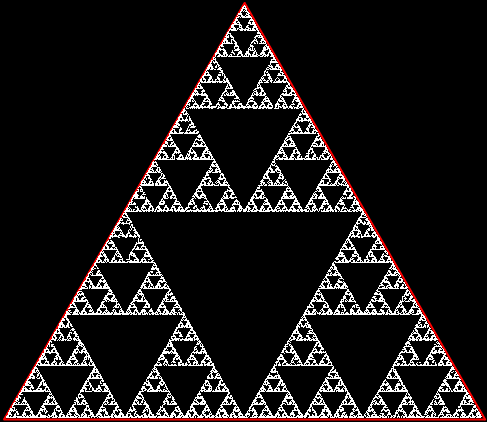
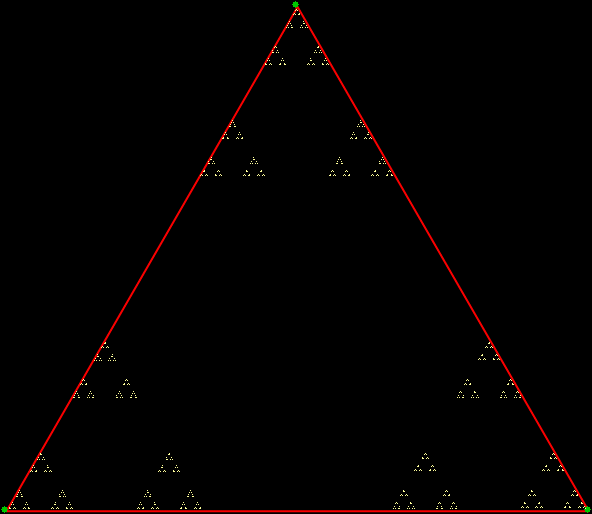
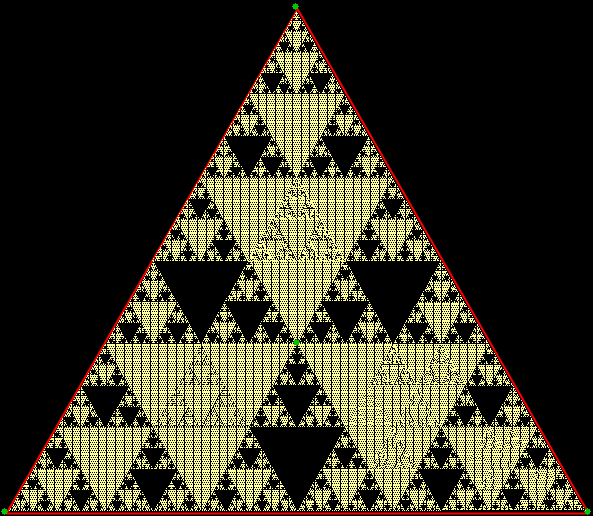
But there’s another way to construct a throwing-star fractal. You use what’s called the chaos game. To understand the commonest form of the chaos game, imagine a ninja inside an equilateral triangle throwing a shuriken again and again halfway towards a randomly chosen vertex of the triangle. If you mark each point where the shuriken lands, you eventually get a fractal called the Sierpiński triangle:

Chaos game with triangle stage 1

Chaos triangle #2

Chaos triangle #3

Chaos triangle #4

Chaos triangle #5

Chaos triangle #6

Chaos triangle #7

Chaos triangle (animated)

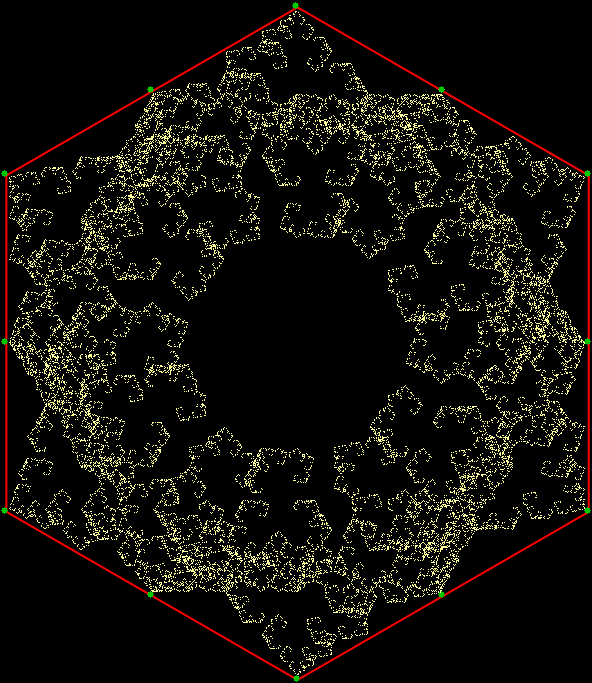
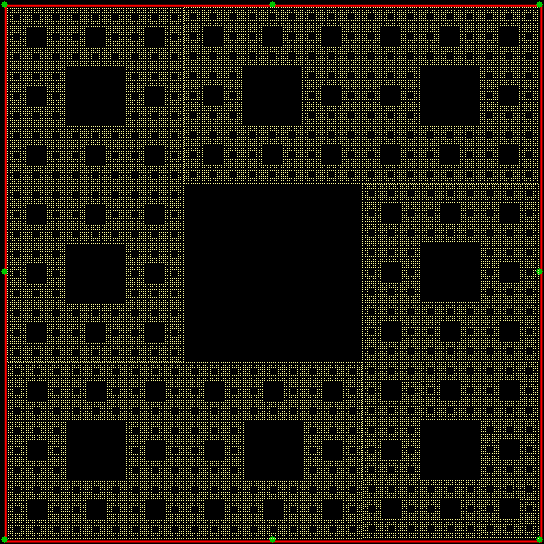
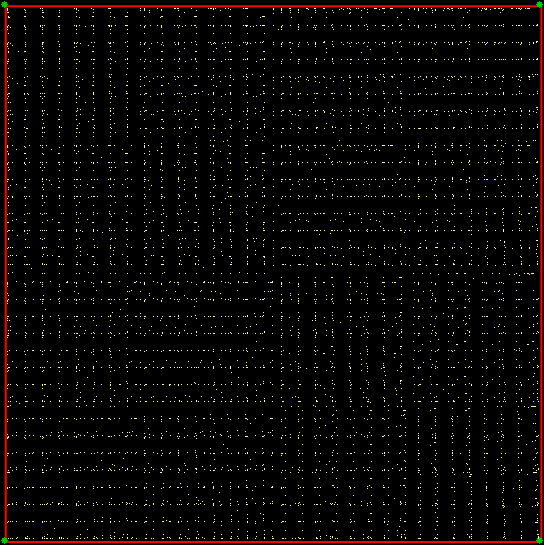
When you try the chaos game with a square, with the ninja throwing the shuriken again and again halfway towards a randomly chosen vertex, you don’t get a fractal. The interior of the square just fills more or less evenly with points:

Chaos game with square, stage 1

Chaos square #2

Chaos square #3

Chaos square #4

Chaos square #5

Chaos square #6

Chaos square (anim)

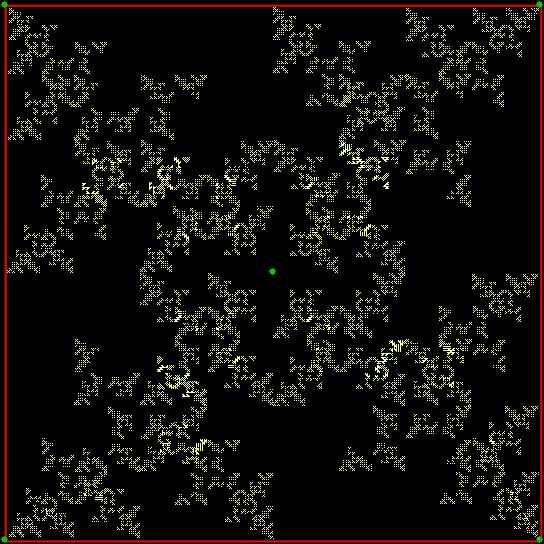
But suppose you restrict the ninja’s throws in some way. If he can’t throw twice or more in a row towards the same vertex, you get a familiar fractal:

Chaos game with square, ban on throwing towards same vertex, stage 1

Chaos square, ban = v+0, #2

Chaos square, ban = v+0, #3

Chaos square, ban = v+0, #4

Chaos square, ban = v+0, #5

Chaos square, ban = v+0, #6

Chaos square, ban = v+0 (anim)

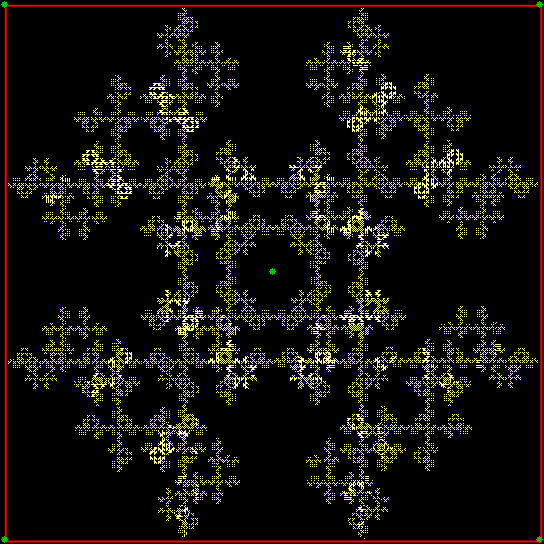
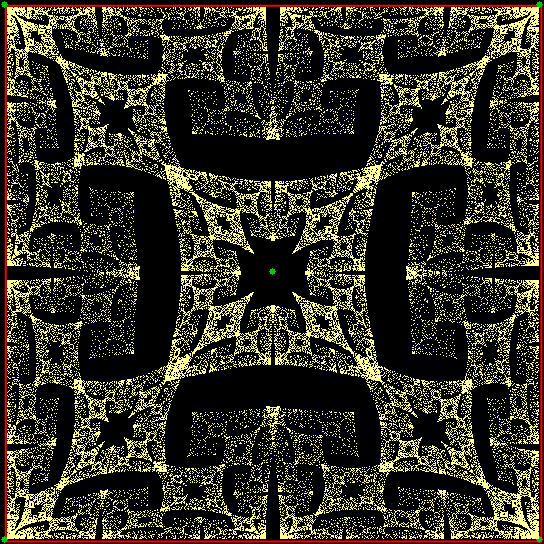
But what if the ninja can’t throw the shuriken towards the vertex one place anti-clockwise of the vertex he’s just thrown it towards? Then you get another familiar fractal — the throwing-star fractal:

Chaos square, ban = v+1, stage 1

Chaos square, ban = v+1, #2

Chaos square, ban = v+1, #3

Chaos square, ban = v+1, #4

Chaos square, ban = v+1, #5

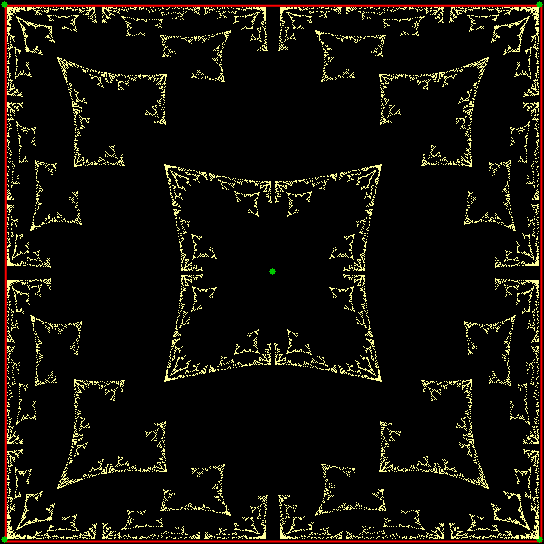
Game of Throwns — throwing-star fractal from chaos game (static)

Game of Throwns — throwing-star fractal from chaos game (anim)

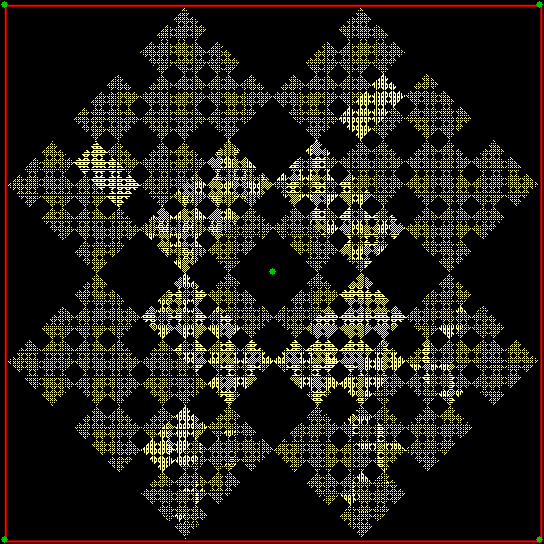
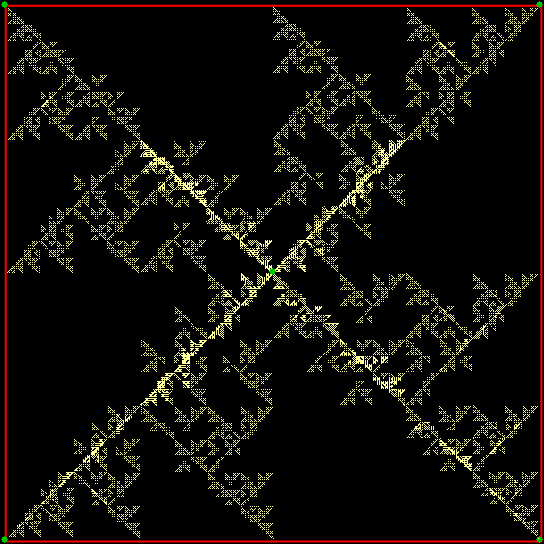
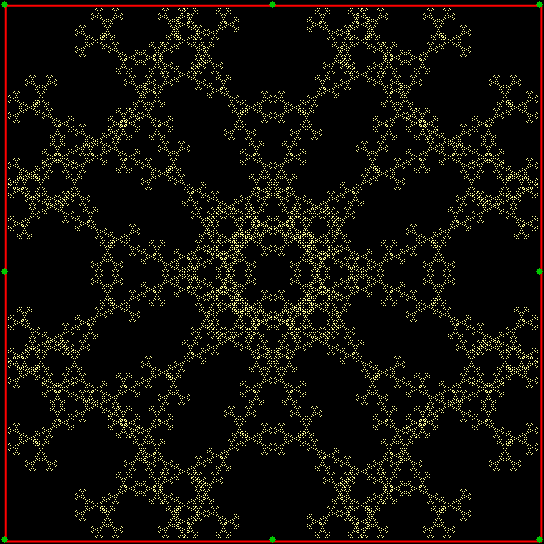
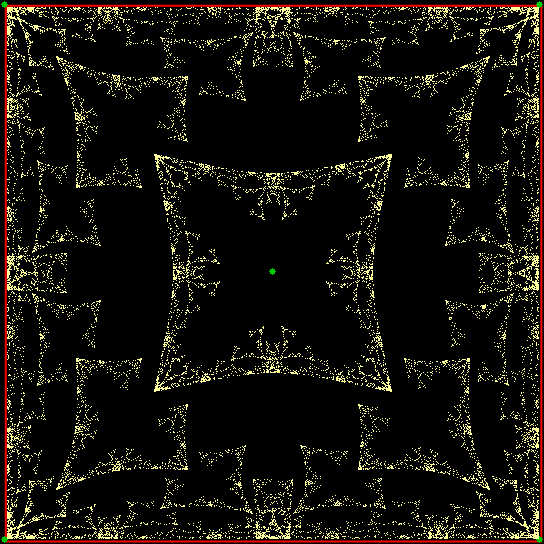
And what if the ninja can’t throw towards the vertex two places anti-clockwise (or two places clockwise) of the vertex he’s just thrown the shuriken towards? Then you get a third familiar fractal — the T-square fractal:

Chaos square, ban = v+2, stage 1

Chaos square, ban = v+2, #2

Chaos square, ban = v+2, #3

Chaos square, ban = v+2, #4

Chaos square, ban = v+2, #5

T-square fractal from chaos game (static)

T-square fractal from chaos game (anim)

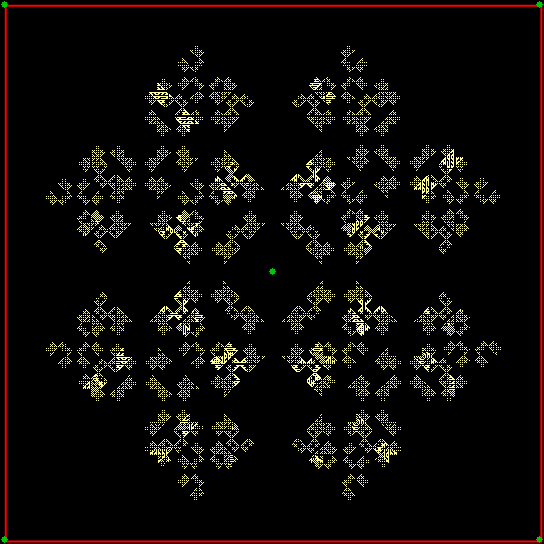
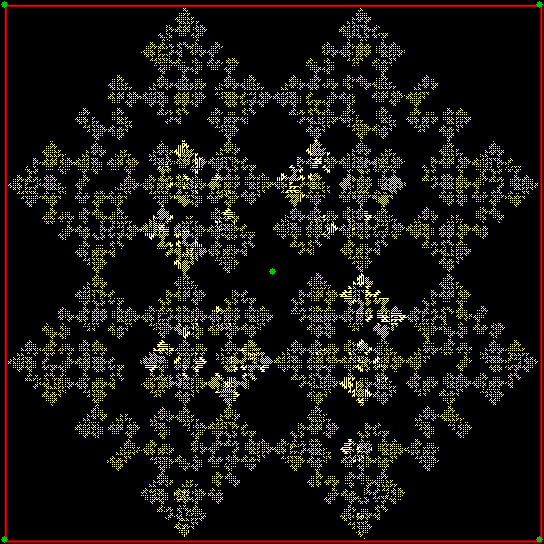
Finally, what if the ninja can’t throw towards the vertex three places anti-clockwise, or one place clockwise, of the vertex he’s just thrown the shuriken towards? If you can guess what happens, your mathematical intuition is much better than mine.

Post-Performative Post-Scriptum

I am not now and never have been a fan of George R.R. Martin. He may be a good author but I’ve always suspected otherwise, so I’ve never read any of his books or seen any of the TV adaptations.

Middlemath

by in Chaos Game, Fractals, Geometry, Mathematics, Pentagons, Squares and tagged , , , , , , , , , , , , , , , , | Leave a comment

Suppose you start at the middle of a triangle, then map all possible ways you can jump eight times half-way towards one or another of the vertices of the triangle. At the end of the eight jumps, you mark your final position with a dot. You could jump eight times towards the same vertex, or once towards vertex 1, once towards vertex 2, and once again towards vertex 1. And so on. If you do this, the record of your jumps looks something like this:

The shape is a fractal called the Sierpiński triangle. But if you try the same thing with a square — map all possible jumping-routes you can follow towards one or another of the four vertices — you simply fill the interior of the square. There’s no interesting fractal:

So you need a plan with a ban. Try mapping all possible routes where you can’t jump towards the same vertex twice in a row. And you get this:

Ban on jumping towards same vertex twice in a row, v(t) ≠ v(t-1)

If you call the current vertex v(t) and the previous vertex v(t-1), the ban says that v(t) ≠ v(t-1). Now suppose you can’t jump towards the vertex one place clockwise of the previous vertex. Now the ban is v(t)-1 ≠ v(t-1) or v(t) ≠ v(t-1)+1 and this fractal appears:

v(t) ≠ v(t-1)+1

And here’s a ban on jumping towards the vertex two places clockwise (or counterclockwise) of the vertex you’ve just jumped towards:

v(t) ≠ v(t-1)+2

And finally the ban on jumping towards the vertex three places clockwise (or one place counterclockwise) of the vertex you’ve just jumped towards:

v(t) ≠ v(t-1)+3 (a mirror-image of v(t) ≠ v(t-1)+1, as above)

Now suppose you introduce a new point to jump towards at the middle of the square. You can create more fractals, but you have to adjust the kind of ban you use. The central point can’t be included in the ban or the fractal will be asymmetrical. So you continue taking account of the vertices, but if the previous jump was towards the middle, you ignore that jump. At least, that’s what I intended, but I wonder whether my program works right. Anyway, here are some of the fractals that it produces:

v(t) ≠ v(t-1) with central point (wcp)

v(t) ≠ v(t-1)+1, wcp

v(t) ≠ v(t-1)+2, wcp

And here are some bans taking account of both the previous vertex and the pre-previous vertex:

v(t) ≠ v(t-1) & v(t) ≠ v(t-2), wcp

v(t) ≠ v(t-1) & v(t-2)+1, wcp

v(t) ≠ v(t-1)+2 & v(t-2), wcp

v(t) ≠ v(t-1) & v(t-2)+1, wcp

v(t) ≠ v(t-1)+1 & v(t-2)+1, wcp

v(t) ≠ v(t-1)+2 & v(t-2)+1, wcp

v(t) ≠ v(t-1)+3 & v(t-2)+1, wcp

v(t) ≠ v(t-1) & v(t-2)+2, wcp

v(t) ≠ v(t-1)+1 & v(t-2)+2, wcp

v(t) ≠ v(t-1)+2 & v(t-2)+2, wcp

Now look at pentagons. They behave more like triangles than squares when you map all possible jumping-routes towards one or another of the five vertices. That is, a fractal appears:

All possible jumping-routes towards the vertices of a pentagon

But the pentagonal-jump fractals get more interesting when you introduce jump-bans:

v(t) ≠ v(t-1)

v(t) ≠ v(t-1)+1

v(t) ≠ v(t-1)+2

v(t) ≠ v(t-1) & v(t-2)

v(t) ≠ v(t-1)+2 & v(t-2)

v(t) ≠ v(t-1)+1 & v(t-2)+1

v(t) ≠ v(t-1)+3 & v(t-2)+1

v(t) ≠ v(t-1)+1 & v(t-2)+2

v(t) ≠ v(t-1)+2 & v(t-2)+2

v(t) ≠ v(t-1)+3 & v(t-2)+2

Finally, here are some pentagonal-jump fractals using a central point:

Post-Performative Post-Scriptum

I’m not sure if I’ve got the order of some bans right above. For example, should v(t) ≠ v(t-1)+1 & v(t-2)+2 really be v(t) ≠ v(t-1)+2 & v(t-2)+1? I don’t know and I’m not going to check. But the idea of jumping-point bans is there and that’s all you need if you want to experiment with these fractal methods for yourself.

Think Inc #2

by in Chaos Game, Fractals, Geometry, Mathematics, Squares and tagged , , , , , , , , , , , , , , | Leave a comment

In a pre-previous post called “Think Inc”, I looked at the fractals created by a point first jumping halfway towards the vertex of a square, then using a set of increments to decide which vertex to jump towards next. For example, if the inc-set was [0, 1, 3], the point would jump next towards the same vertex, v[i]+0, or the vertex immediately clockwise, v[i]+1, or the vertex immediately anti-clockwise, v[i]+3. And it would trace all possible routes using that inc-set. Then I added refinements to the process like giving the point extra jumping-targets half-way along each side.

Here are some more variations on the inc-set theme using two and three extra jumping-targets along each side of the square. First of all, try two extra jumping-targets along each side and a set of three increments:

inc = 0, 1, 6

inc = 0, 2, 6

inc = 0, 2, 8

inc = 0, 3, 6

inc = 0, 3, 9

inc = 0, 4, 8

inc = 0, 5, 6

inc = 0, 5, 7

inc = 1, 6, 11

inc = 2, 6, 10

inc = 3, 6, 9

Now try two extra jumping-targets along each side and a set of four increments:

inc = 0, 1, 6, 11

inc = 0, 2, 8, 10

inc = 0, 3, 7, 9

inc = 0, 4, 8, 10

inc = 0, 5, 6, 7

inc = 0, 5, 7, 8

inc = 1, 6, 7, 9

inc = 1, 4, 6, 11

inc = 1, 5, 7, 11

inc = 2, 4, 8, 10

inc = 3, 5, 7, 9

And finally, three extra jumping-targets along each side and a set of three increments:

inc = 0, 3, 13

inc = 0, 4, 8

inc = 0, 4, 12

inc = 0, 5, 11

inc = 0, 6, 9

inc = 0, 7, 9

Previously Pre-Posted

• Think Inc — an earlier look at inc-set fractals

Think Inc

by in Chaos Game, Fractals, Geometry, Hexagons, Mathematics, Pentagons, Squares and tagged , , , , , , , , , , , , , , , | Leave a comment

This is a T-square fractal:

T-square fractal

Or you could say it’s a T-square fractal with the scaffolding taken away, because there’s nothing to show how it was made. And how is a T-square fractal made? There are many ways. One of the simplest is to set a point jumping 1/2 of the way towards one or another of the four vertices of a square. If the point is banned from jumping towards the vertex two places clockwise (or counter-clockwise) of the vertex, v[i=1..4], it’s just jumped towards, you get a T-square fractal by recording each spot where the point lands.

You also get a T-square if the point is banned from jumping towards the vertex most distant from the vertex, v[i], it’s just jumped towards. The most distant vertex will always be the diagonally opposite vertex, or the vertex, v[i+2], two places clockwise of v[i]. So those two bans are functionally equivalent.

But what if you don’t talk about bans at all? You can also create a T-square fractal by giving the point three choices of increment, [0,1,3], after it jumps towards v[i]. That is, it can jump towards v[i+0], v[i+1] or v[i+3] (where 3+2 = 5 → 5-4 = 1; 3+3 = 6 → 2; 4+1 = 5 → 1; 4+2 = 6 → 2; 4+3 = 7 → 3). Vertex v[i+0] is the same vertex, v[i+1] is the vertex one place clockwise of v[i], and v[i+3] is the vertex two places clockwise of v[i].

So this method is functionally equivalent to the other two bans. But it’s easier to calculate, because you can take the current vertex, v[i], and immediately calculate-and-use the next vertex, without having to check whether the next vertex is forbidden. In other words, if you want speed, you just have to Think Inc!

Speed becomes important when you add a new jumping-target to each side of the square. Now the point has 8 possible targets to jump towards. If you impose several bans on the next jump, e.g the point can’t jump towards v[i+2], v[i+3], v[i+5], v[i+6] and v[i+7], you will have to check for five forbidden targets. But using the increment-set [0,1,4] you don’t have to check for anything. You just inc-and-go:

inc = 0, 1, 4

Here are more fractals created with the speedy inc-and-go method:

inc = 0, 2, 3

inc = 0, 2, 5

inc = 0, 3, 4

inc = 0, 3, 5

inc = 1, 4, 7

inc = 2, 4, 7

inc = 0, 1, 4, 7

inc = 0, 3, 4, 5

inc = 0, 3, 4, 7

inc = 0, 4, 5, 7

inc = 1, 2, 6, 7

With more incs, there are more possible paths for the jumping point and the fractals become more “solid”:

inc = 0, 1, 2, 4, 5

inc = 0, 1, 2, 6, 7

inc = 0, 1, 3, 5, 7

Now try applying inc-and-go to a pentagon:

inc = 0, 1, 2

(open in new window if blurred)

inc = 0, 2, 3

And add a jumping-target to each side of the pentagon:

inc = 0, 2, 5

inc = 0, 3, 6

inc = 0, 3, 7

inc = 1, 5, 9

inc = 2, 5, 8

inc = 5, 6, 9

And add two jumping-targets to each side of the pentagon:

inc = 0, 1, 7

inc = 0, 2, 12

inc = 0, 3, 11

inc = 0, 3, 12

inc = 0, 4, 11

inc = 0, 5, 9

inc = 0, 5, 10

inc = 2, 7, 13

inc = 2, 11, 13

inc = 3, 11, 13

After the pentagon comes the hexagon:

inc = 0, 1, 2

inc = 0, 1, 5

inc = 0, 3, 4

inc = 0, 3, 5

inc = 1, 3, 5

inc = 2, 3, 4

Add a jumping-target to each side of the hexagon:

inc = 0, 2, 5

inc = 0, 2, 9

inc = 0, 6, 11

inc = 0, 3, 6

inc = 0, 3, 8

inc = 0, 3, 9

inc = 0, 4, 7

inc = 0, 4, 8

inc = 0, 5, 6

inc = 0, 5, 8

inc = 1, 5, 9

inc = 1, 6, 10

inc = 1, 6, 11

inc = 2, 6, 8

inc = 2, 6, 10

inc = 3, 5, 7

inc = 3, 6, 9

inc = 6, 7, 11

Boole(b)an #3

by in Chaos Game, Fractals, Geometry, Mathematics, Squares and tagged , , , , , , , , , , , , , , , | Leave a comment

In the posts “Boole(b)an #1″ and “Boole(b)an #2” I looked at fractals created by certain kinds of ban on a point jumping (quasi-)randomly towards the four vertices, v=1..4, of a square. For example, suppose the program has a vertex-history of 2, that is, it remembers two jumps into the past, the previous jump and the pre-previous jump. There are sixteen possible combinations of pre-previous and previous jumps: [1,1], [1,2], 1,3] … [4,2], [4,3], [4,4].

Let’s suppose the program bans 4 of those 16 combinations by reference to the current possible jump. For example, it might ban [0,0]; [0,1]; [0,3]; [2,0]. To see what that means, let’s suppose the program has to decide at some point whether or not to jump towards v=3. It will check whether the combination of pre-previous and previous jumps was [3+0,3+0] = [3,3] or [3+0,3+1] = [3,4] or [3+0,3+3] = [3,2] or [3+2,3+0] = [1,3] (when the sum > 4, v = sum-4). If the previous combination is one of those pairs, it bans the jump towards v=3 and chooses another vertex; otherwise, it jumps towards v=3 and updates the vertex-history. This is the fractal that appears when those bans are used:

ban = [0,0]; [0,1]; [0,3]; [2,0]

And here are more fractals using a vertex-history of 2 and a ban on 4 of 16 possible combinations of pre-previous and previous jump:

ban = [0,0]; [0,1]; [0,3]; [2,2]

ban = [0,0]; [0,2]; [1,0]; [3,0]

ban = [0,0]; [0,2]; [1,1]; [3,3]

ban = [0,0]; [0,2]; [1,3]; [3,1]

ban = [0,0]; [1,0]; [2,2]; [3,0]

ban = [0,0]; [1,1]; [1,2]; [3,2]

Continue reading “Boole(b)an #3”…

Elsewhere other-engageable

• Boole(b)an #1
• Boole(b)an #2

Root Routes

by in Chaos Game, Fractals, Geometry, Mathematics, Square Roots, Squares, Triangles and tagged , , , , , , , , , , , , , , | Leave a comment

Suppose a point traces all possible routes jumping half-way towards the three vertices of an equilateral triangle. A special kind of shape appears — a fractal called the Sierpiński triangle that contains copies of itself at smaller and smaller scales:

Sierpiński triangle, jump = 1/2

And what if the point jumps 2/3rds of the way towards the vertices as it traces all possible routes? You get this dull fractal:

Triangle, jump = 2/3

But if you add targets midway along each side of the triangle, you get this fractal with the 2/3rds jump:

Triangle, jump = 2/3, side-targets

Now try the 1/2-jump triangle with a target at the center of the triangle:

Triangle, jump = 1/2, central target

And the 2/3-jump triangle with side-targets and a central target:

Triangle, jump = 2/3, side-targets, central target

But why stop at simple jumps like 1/2 and 2/3? Let’s take the distance to the target, td, and use the function 1-(sqrt(td/7r)), where sqrt() is the square-root and 7r is 7 times the radius of the circumscribing circle:

Triangle, jump = 1-(sqrt(td/7r))

Here’s the same jump with a central target:

Triangle, jump = 1-(sqrt(td/7r)), central target

Now let’s try squares with various kinds of jump. A square with a 1/2-jump fills evenly with points:

Square, jump = 1/2 (animated)

The 2/3-jump does better with a central target:

Square, jump = 2/3, central target

Or with side-targets:

Square, jump = 2/3, side-targets

Now try some more complicated jumps:

Square, jump = 1-sqrt(td/7r)

Square, jump = 1-sqrt(td/15r), side-targets

And what if you ban the point from jumping twice or more towards the same target? You get this fractal:

Square, jump = 1-sqrt(td/6r), ban = prev+0

Now try a ban on jumping towards the target two places clockwise of the previous target:

Square, jump = 1-sqrt(td/6r), ban = prev+2

And the two-place ban with a central target:

Square, jump = 1-sqrt(td/6r), ban = prev+2, central target

And so on:

Square, jump = 1-sqrt(td/6.93r), ban = prev+2, central target

Square, jump = 1-sqrt(td/7r), ban = prev+2, central target

These fractals take account of the previous jump and the pre-previous jump:

Square, jump = 1-sqrt(td/4r), ban = prev+2,2, central target

Square, jump = 1-sqrt(td/5r), ban = prev+2,2, central target

Square, jump = 1-sqrt(td/6r), ban = prev+2,2, central target

Elsewhere other-accessible

• Boole(b)an #2 — fractals created in similar ways

This Charming Dis-Arming

by in Chaos Game, Fractals, Geometry, Mathematics, Squares, Triangles and tagged , , , , , , , , , , , , , , , , , , | Leave a comment

One of the charms of living in an old town or city is finding new routes to familiar places. It’s also one of the charms of maths. Suppose a three-armed star sprouts three half-sized arms from the end of each of its three arms. And then sprouts three quarter-sized arms from the end of each of its nine new arms. And so on. This is what happens:

Three-armed star

3-Star sprouts more arms

Sprouting 3-Star #3

Sprouting 3-Star #4

Sprouting 3-Star #5

Sprouting 3-Star #6

Sprouting 3-Star #7

Sprouting 3-Star #8

Sprouting 3-Star #9

Sprouting 3-Star #10

Sprouting 3-Star #11 — the Sierpiński triangle

Sprouting 3-star (animated)

The final stage is a famous fractal called the Sierpiński triangle — the sprouting 3-star is a new route to a familiar place. But what happens when you trying sprouting a four-armed star in the same way? This does:

Four-armed star #1

Sprouting 4-Star #2

Sprouting 4-Star #3

Sprouting 4-Star #4

Sprouting 4-Star #5

Sprouting 4-Star #6

Sprouting 4-Star #7

Sprouting 4-Star #8

Sprouting 4-Star #9

Sprouting 4-Star #10

Sprouting 4-star (animated)

There’s no obvious fractal with a sprouting 4-star. Not unless you dis-arm the 4-star in some way. For example, you can ban any new arm sprouting in the same direction as the previous arm:

Dis-armed 4-star (+0) #1

Dis-armed 4-Star (+0) #2

Dis-armed 4-Star (+0) #3

Dis-armed 4-Star (+0) #4

Dis-armed 4-Star (+0) #5

Dis-armed 4-Star (+0) #6

Dis-armed 4-Star (+0) #7

Dis-armed 4-Star (+0) #8

Dis-armed 4-Star (+0) #9

Dis-armed 4-Star (+0) #10

Dis-armed 4-star (+0) (animated)

Once again, it’s a new route to a familiar place (for keyly committed core components of the Overlord-of-the-Über-Feral community, anyway). Now try banning an arm sprouting one place clockwise of the previous arm:

Dis-armed 4-Star (+1) #1

Dis-armed 4-Star (+1) #2

Dis-armed 4-Star (+1) #3

Dis-armed 4-Star (+1) #4

Dis-armed 4-Star (+1) #5

Dis-armed 4-Star (+1) #6

Dis-armed 4-Star (+1) #7

Dis-armed 4-Star (+1) #8

Dis-armed 4-Star (+1) #9

Dis-armed 4-Star (+1) #10

Dis-armed 4-Star (+1) (animated)

Again it’s a new route to a familiar place. Now trying banning an arm sprouting two places clockwise (or anti-clockwise) of the previous arm:

Dis-armed 4-Star (+2) #1

Dis-armed 4-Star (+2) #2

Dis-armed 4-Star (+2) #3

Dis-armed 4-Star (+2) #4

Dis-armed 4-Star (+2) #5

Dis-armed 4-Star (+2) #6

Dis-armed 4-Star (+2) #7

Dis-armed 4-Star (+2) #8

Dis-armed 4-Star (+2) #9

Dis-armed 4-Star (+2) #10

Dis-armed 4-Star (+2) (animated)

Once again it’s a new route to a familiar place. And what happens if you ban an arm sprouting three places clockwise (or one place anti-clockwise) of the previous arm? You get a mirror image of the Dis-armed 4-Star (+1):

Dis-armed 4-Star (+3)

Here’s the Dis-armed 4-Star (+1) for comparison:

Dis-armed 4-Star (+1)

Elsewhere other-accessible

• Boole(b)an #2 — other routes to the fractals seen above

Boole(b)an #2

by in Chaos Game, Fractals, Geometry, Mathematics, Squares and tagged , , , , , , , , , , , , , , , | Leave a comment

In “Boole(b)an”, I looked at some of the things that happen when you impose bans of different kinds on a point jumping half-way towards a randomly chosen vertex of a square. If the point can’t jump towards the same vertex twice (or more) in a row, you get the fractal below (or rather, you get a messier version of the fractal below, because I’ve used an algorithm that finds all possible routes to create the fractals in this post):

ban = v(i) + 0

If the point can’t jump towards the vertex one place clockwise of the point it has just jumped towards, you get this fractal:

ban = v(i) + 1

If the point can’t jump towards the vertex two places clockwise (or anti-clockwise) of the point it has just jumped towards, you get this fractal:

ban = v(i) + 2

Finally, you get a mirror-image of the one-place-clockwise fractal when the ban is on jumping towards the vertex three places clockwise (or one place anti-clockwise) of the previous vertex:

ban = v(i) + 3

Now let’s introduce the concept of “vertex-history”. The four fractals above use a vertex-history of 1, vh = 1, because they look one step into the past, at the previously chosen vertex. Because there are four vertices, there are four possible previous vertices. But when vh = 2, you’re taking account of both the previous vertex, v(i), and what you might call the pre-previous vertex, v(i-1). There are sixteen possible combinations of previous vertex and pre-previous vertex (16 = 4 x 4).

Now, suppose the jump-ban is imposed when one of two conditions is met: the vertex is 1) one place clockwise of the previous vertex and the same as the pre-previous vertex; 2) three places clockwise of the previous chosen vertex and the same as the pre-previous vertex. So the boolean test is (condition(1) AND condition(2)) OR (condition(3) AND condition(4)). When you apply the test, you get this fractal:

ban = v(i,i-1) + [0,1] or v(i,i-1) + [0,3]

The fractal looks more complex, but I think it’s a blend of some combination of the four classic fractals shown at the beginning of this post. Here are more multiple-ban fractals using vh = 2 and bani = 2:

ban = [0,1] or [1,1]

ban = [0,2] or [2,0]

ban = [0,2] or [2,2]

ban = [1,0] or [3,0]

ban = [1,1] or [3,3]

ban = [1,2] or [2,2]

ban = [1,2] or [3,2]

ban = [1,3] or [2,0]

ban = [1,3] or [3,1]

ban = [2,0] or [2,2]

ban = [2,1] or [2,3]

For the fractals below, vh = 2 and bani = 3 (i.e., bans are imposed when one of three possible conditions is met). Again, I think the fractals are blends of some combination of the four classic ban-fractals shown at the beginning of this post:

ban = [0,0] or [1,2] or [3,2]

ban = [0,0] or [1,3] or [3,1]

ban = [0,0] or [2,1] or [2,3]

ban = [0,1] or [0,2] or [0,3]

ban = [0,1] or [0,3] or [1,1]

ban = [0,1] or [0,3] or [2,0]

ban = [0,1] or [0,3] or [2,2]

ban = [0,1] or [1,1] or [1,2]

ban = [0,1] or [1,1] or [3,0]

ban = [0,1] or [1,2] or [3,2]

ban = [0,2] or [1,0] or [3,0]

ban = [0,2] or [1,1] or [3,3]

ban = [0,2] or [1,2] or [2,2]

ban = [0,2] or [1,2] or [3,1]

ban = [0,2] or [1,2] or [3,2]

ban = [0,2] or [1,3] or [2,0]

ban = [0,2] or [1,3] or [3,1]

ban = [0,2] or [2,0] or [2,2]

ban = [0,2] or [2,1] or [2,3]

ban = [0,2] or [2,2] or [3,2]

ban = [0,3] or [1,0] or [2,0]

ban = [1,0] or [1,2] or [3,0]

ban = [1,0] or [2,2] or [3,0]

ban = [1,1] or [2,0] or [3,3]

ban = [1,1] or [2,1] or [3,1]

ban = [1,1] or [2,2] or [3,3]

ban = [1,1] or [2,3] or [3,3]

ban = [1,2] or [2,0] or [3,1]

ban = [1,2] or [2,0] or [3,2]

ban = [1,2] or [2,1] or [2,3]

ban = [1,2] or [2,3] or [3,2]

ban = [1,2] or [3,2] or [3,3]

ban = [1,3] or [2,0] or [2,2]

ban = [1,3] or [2,0] or [3,0]

ban = [1,3] or [2,0] or [3,1]

ban = [1,3] or [2,2] or [3,1]

ban = [2,0] or [3,1] or [3,2]

ban = [2,1] or [2,3] or [3,2]

Previously pre-posted

Boole(b)an — an early look at ban-fractals

Boole(b)an

by in Chaos Game, Fractals, Geometry, Mathematics, Squares and tagged , , , , , , , , , , | Leave a comment

Suppose you allow a point to jump at random half-way towards one of the four vertices of a square. But not entirely at random — you ban the point from jumping towards the same vertex twice (or more) in a row. You get this pattern:

ban on v(i) + 0

It’s a fractal, that is, a shape that contains smaller and smaller copies of itself. Next you ban the point from jumping towards the vertex one place clockwise of the vertex it last jumped towards (i.e., it can jump towards, say, vertex 2 as many times as it likes, but it can’t jump towards vertex 2+1 = 3, and so on). You get this fractal:

ban on v(i) + 1

Now ban it from jumping towards the vertex two places clockwise of the vertex it last jumped towards (i.e., it can’t jump towards the diagonally opposite vertex). You get this fractal:

ban on v(i) + 2

And if you ban the point from jumping towards the vertex three places clockwise of the last vertex, you get a mirror-image of the v(i)+1 fractal (see above):

ban on v(i) + 3

The fractals above have a memory one vertex into the past: the previous vertex. Let’s try some fractals with a memory two vertices into the past: the previous vertex and the pre-previous vertex (and even the pre-pre-previous vertex).

But this time, let’s suppose that sometimes the point can’t jump if the previous or pre-previous isn’t equal to v(i) + n. So sometimes the jump is banned when the test is true, sometimes when the test is false — you might call it a boolean ban or boole(b)an. Using boole(b)ans, you can get this set of fractals:

With these fractals, the boolean test sends the point back to the center of the square:

Posteriously post-posted

Boole(b)an #2 — a later look at ban-fractals