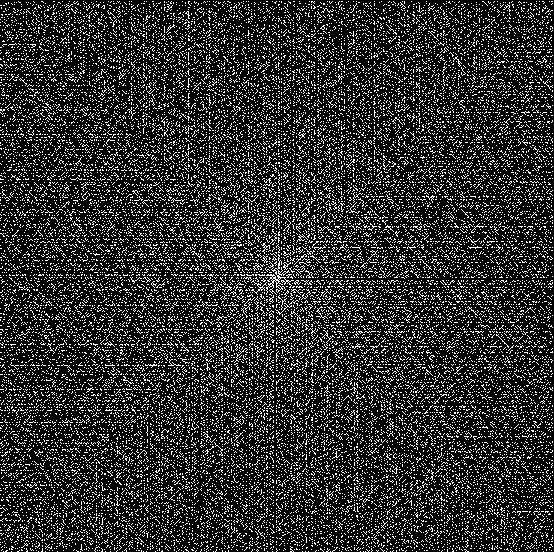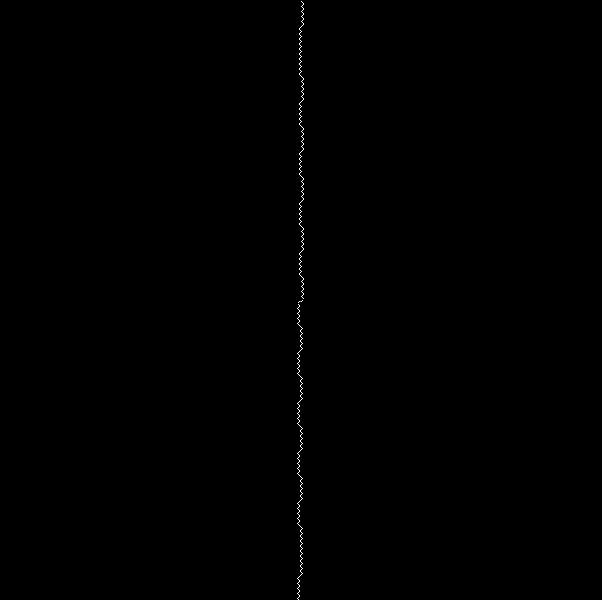What’s the next number in this sequence?
1, 3, 0, 4, 9, 15, 8, 0, 9, 19, 30, 42, 29, 15, 0, 16, 33, 51, 70, 90, 69, 47, 24, 0, 25, ?
Even if you can’t work out the full rule generating the sequence, you may be able to deduce that the next number is… 51. There’s a pattern involving 0:
1, 3, 0, 4, 9, 15, 8, 0, 9, 19, 30, 42, 29, 15, 0, 16, 33, 51, 70, 90, 69, 47, 24, 0, 25... → 3, 0, 4, 9, [...] 8, 0, 9, 19, [...] 15, 0, 16, 33, [...] 24, 0, 25...
The first number after each 0 is 1 more than the first number before the 0. The second number after the 0 is equal to 2 * (first-number-after 0) + 1. So:
1, 3, 0, 4, 2*4+1 = 9, [...] 8, 0, 9, 2*9+1 = 19, [...] 15, 0, 16, 2*16+1 = 33, [...] 24, 0, 25, 2*25+1 = 51...
But what is the full rule for generating the sequence? It’s based on this pattern of sums I noticed:
1+2 = 3
4+5+6 = 7+8 = 15
9+10+11+12 = 13+14+15 = 42
16+17+18+19+20 = 21+22+23+24 = 90
25+26+27+28+29+30 = 31+32+33+34+35 = 165
36+37+38+39+40+41+42 = 43+44+45+46+47+48 = 273
49+50+51+52+53+54+55+56 = 57+58+59+60+61+62+63 = 420
64+65+66+67+68+69+70+71+72 = 73+74+75+76+77+78+79+80 = 612 — See A059270 at the OEIS
The sum of the first two integers (1+2) equals the next integer (3). The sum of the next three integers (4+5+6) equals the sum of the next two integers (7+8). The sum of the next four integers (9+10+11+12) equals the sum of the next three integers (13+14+15). And so on. The sequence is based on an adaptation of that pattern:
1 + 2 - 3 = 0
4 + 5 + 6 - 7 - 8 = 0
9 + 10 + 11 + 12 - 13 - 14 - 15 = 0
16 + 17 + 18 + 19 + 20 - 21 - 22 - 23 - 24 = 0
25 + 26 + 27 + 28 + 29 + 30 - 31 - 32 - 33 - 34 - 35 = 0↓
1 + 2 - 3 + 4 + 5 + 6 - 7 - 8 + 9 + 10 + 11 + 12 - 13 - 14 - 15 + 16 + 17 + 18 + 19 + 20 - 21 - 22 - 23 - 24 + 25 + 26 + 27 + 28 + 29 + 30 - 31 - 32 - 33 - 34 - 35...
If you work out the partial sums of the additions and subtractions, you get the sequence I started with, which regularly rises to a new high, then falls back to 0:
1, 3, 0, 4, 9, 15, 8, 0, 9, 19, 30, 42, 29, 15, 0, 16, 33, 51, 70, 90, 69, 47, 24, 0, 25, 51, 78, 106, 135, 165, 134, 102, 69, 35, 0, 36, 73, 111, 150, 190, 231, 273, 230, 186, 141, 95, 48, 0, 49, 99, 150, 202, 255, 309, 364, 420, 363, 305, 246, 186, 125, 63, 0, 64, 129, 195, 262, 330, 399, 469, 540, 612, 539, 465, 390, 314, 237, 159, 80, 0, 8
1, 163, 246, 330, 415, 501, 588, 676, 765, 855, 764, 672, 579, 485, 390, 294, 197, 99, 0, 100...
When you represent the numbers of the sequence on an Ulam-like spiral, you get this pattern of lines (and zigzags) against a haze of less regular points:
Spiral for pos2neg1 = 1, 3, 0, 4, 9, 15, 8, 0, 9, 19, 30, 42, 29, 15, 0, 16, 33…
I’ll call the lines spiral artefacts. I don’t know what generates all of them, but the zigzag diagonal from top left to bottom right is partly created by the square numbers. Here’s the spiral at higher resolutions:
Spiral for pos2neg1 (x2)
Spiral for pos2neg1 (x4)
You’ll find more of the lines if you look at Ulam-like spirals for adaptations of the original sequence. Suppose you add the first three integers, then take away the next two, then add the next four integers, then take away the next three, and so on: 1 + 2 + 3 – 4 – 5 + 6 + 7 + 8 + 9 – 10 – 11 – 12 + 13 + 14… Here are the partials sums of these additions and subtractions:
1, 3, 6, 2, -3, 3, 10, 18, 27, 17, 6, -6, 7, 21, 36, 52, 69, 51, 32, 12, -9, 13, 36, 60, 85, 111, 138, 110, 81, 51, 20, -12, 21, 55, 90, 126, 163, 201, 240, 200, 159, 117, 74, 30, -15, 31, 78, 126, 175, 225, 276, 328, 381, 327, 272, 216, 159, 101, 42, -18, 43, 105, 168, 232, 297, 363, 430, 498, 567, 497, 426, 354, 281, 207, 132, 56, -21, 57, 136, 216, 297, 379, 462, 546, 631, 717, 804, 716, 627, 537, 446, 354, 261, 167, 72, -24, 73, 171, 270, 370...
If the original sequence is pos2neg1 (add first two integers, take away next one integer, etc), this adapted sequence is pos3neg2 (add first three integers, take away next two, etc). Here’s the spiral for pos3neg2 (with negative numbers represented as positive):
Spiral for pos3neg2 = 1, 3, 6, 2, -3, 3, 10, 18, 27, 17, 6, -6, 7, 21, 36, 52,
69, 51, 32, 12…
Note that the spiral is incomplete and some of the lines not fully extended, because the lines are easier to see when the sequence doesn’t carry on too long and clutter the screen. Here are more adapted sequences shown on Ulam-like spirals (again, some of the spirals are incomplete):
Spiral for pos4neg3 = 1, 3, 6, 10, 5, -1, -8, 0, 9, 19, 30, 42, 29, 15, 0, -16, 1, 19, 38, 58…
Spiral for pos5neg4 = 1, 3, 6, 10, 15, 9, 2, -6, -15, -5, 6, 18, 31, 45, 60, 44, 27, 9, -10, -30…
Spiral for pos6neg5 = 1, 3, 6, 10, 15, 21, 14, 6, -3, -13, -24, -12, 1, 15, 30, 46, 63, 81, 62, 42…
Spiral for pos7neg6 = 1, 3, 6, 10, 15, 21, 28, 20, 11, 1, -10, -22, -35, -21, -6, 10, 27, 45, 64, 84…
Spiral for pos8neg7 = 1, 3, 6, 10, 15, 21, 28, 36, 27, 17, 6, -6, -19, -33, -48, -32, -15, 3, 22, 42…
Spiral for pos9neg8 = 1, 3, 6, 10, 15, 21, 28, 36, 45, 35, 24, 12, -1, -15, -30, -46, -63, -45, -26, -6…
Spiral for pos10neg9 = 1, 3, 6, 10, 15, 21, 28, 36, 45, 55, 44, 32, 19, 5, -10, -26, -43, -61, -80, -60…
Spiral for pos11neg10 = 1, 3, 6, 10, 15, 21, 28, 36, 45, 55, 66, 54, 41, 27, 12, -4, -21, -39, -58, -78…
Elsewhere Other-Engageable
• Spiral Artefact #1 — different patterns on an Ulam-like spiral
• Spiral Artefact #2 — more different patterns