Category Archives: Pursuit Curves

Mice Thrice

by in Geometry, Mathematics, Pursuit Curves and tagged , , , , , , , , , , , , | Leave a comment

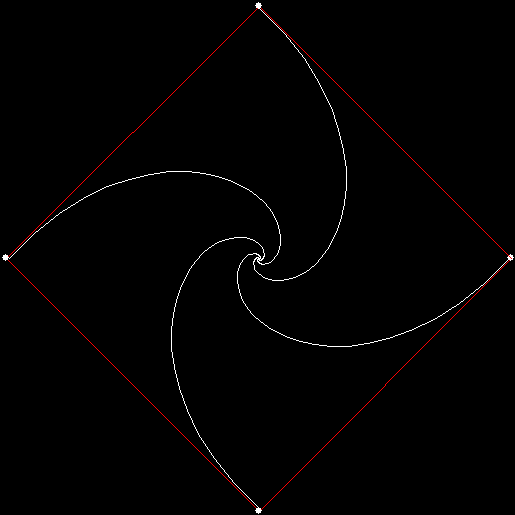
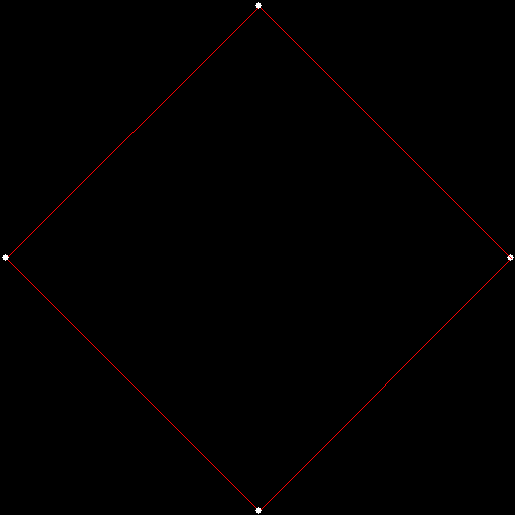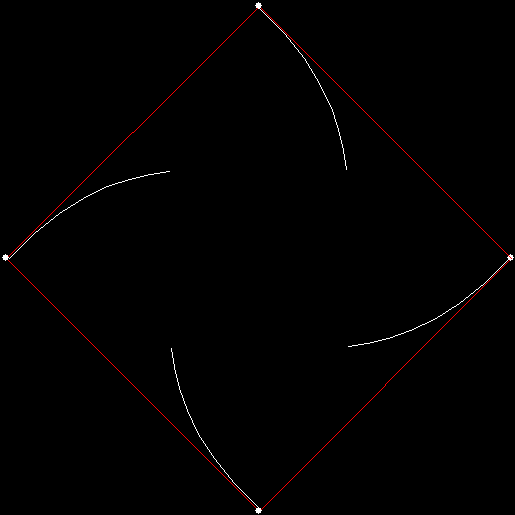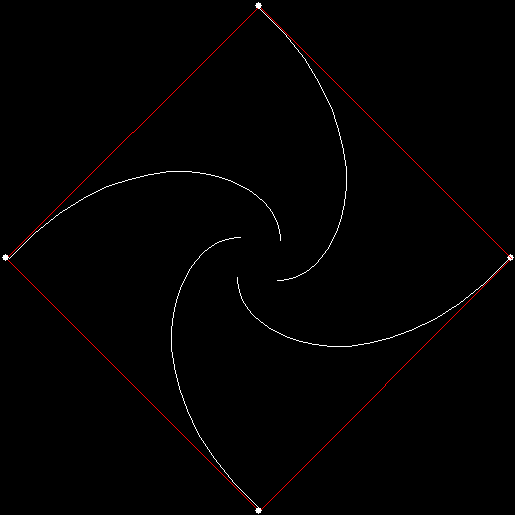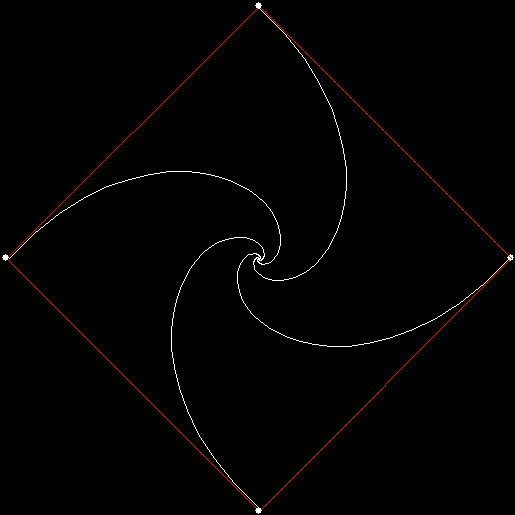
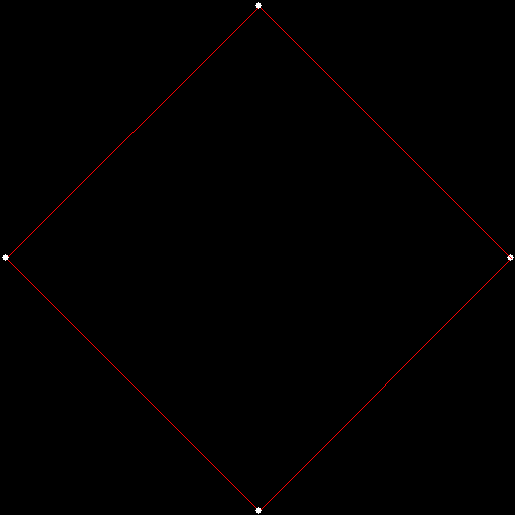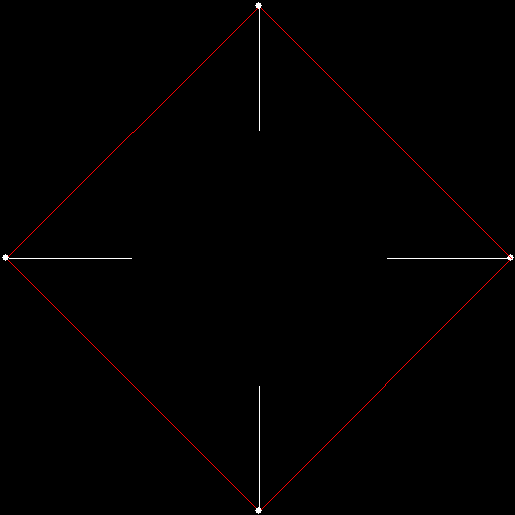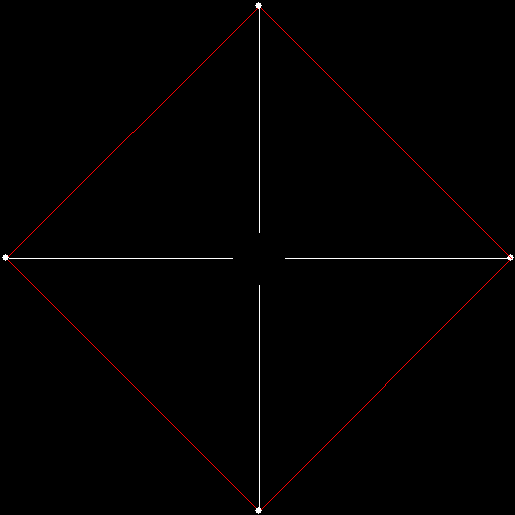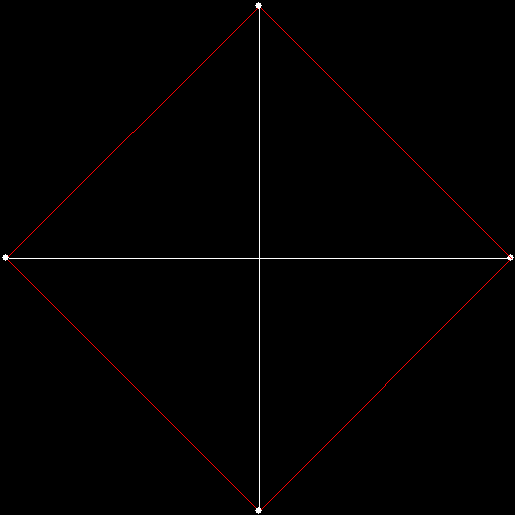
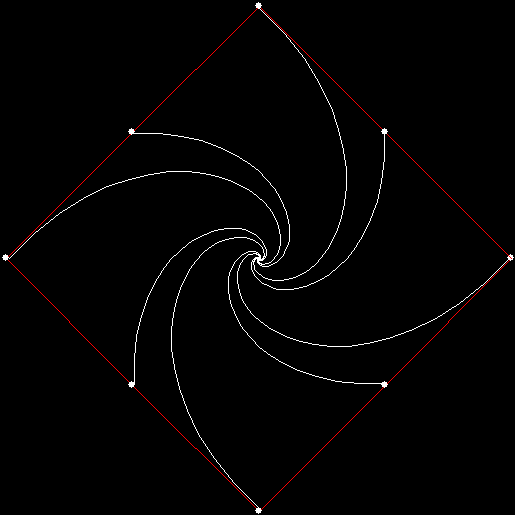
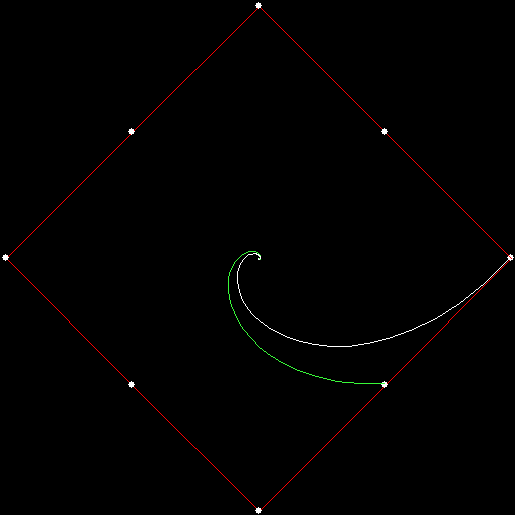
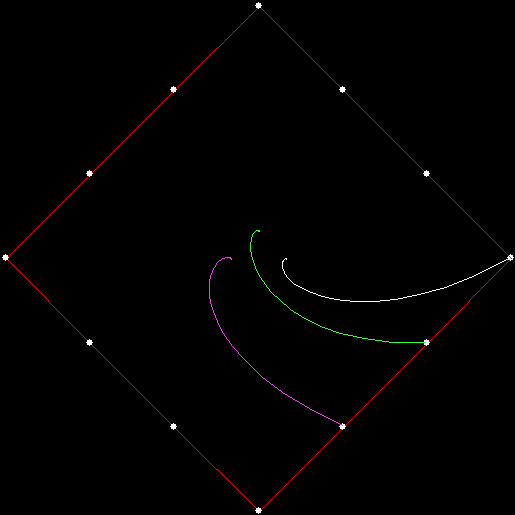
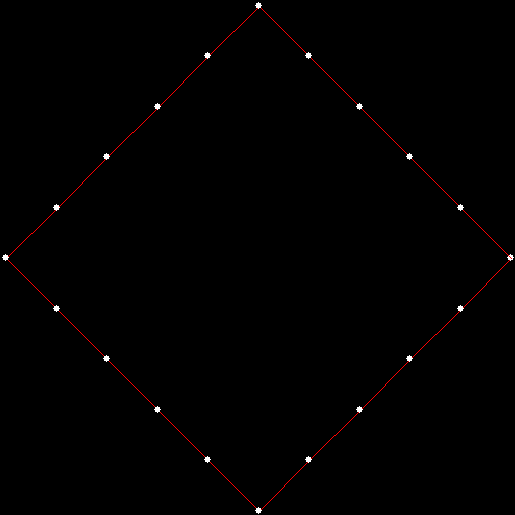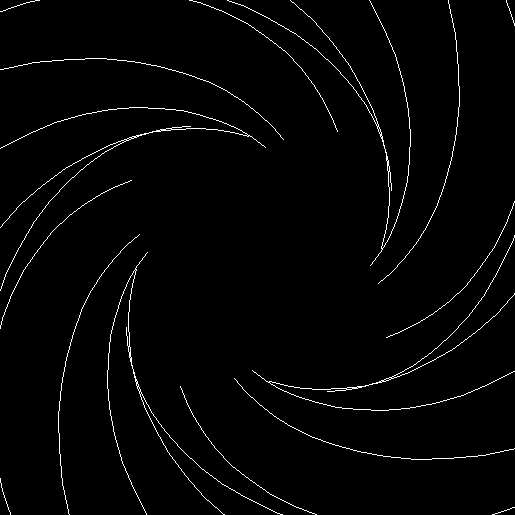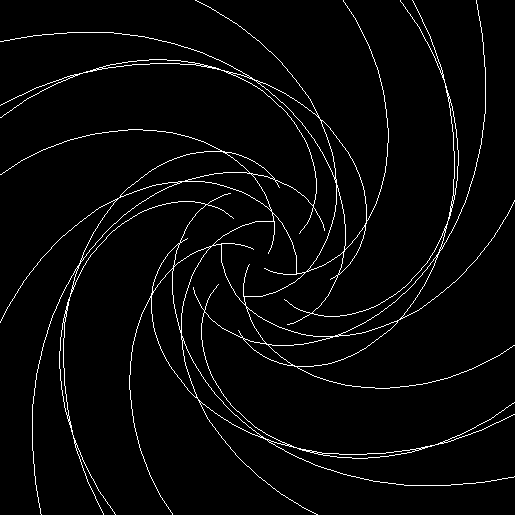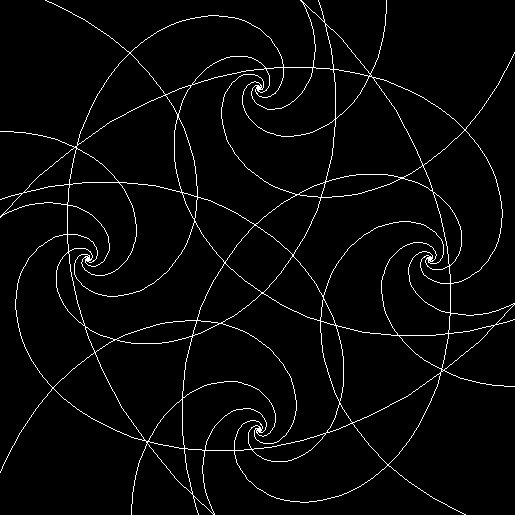
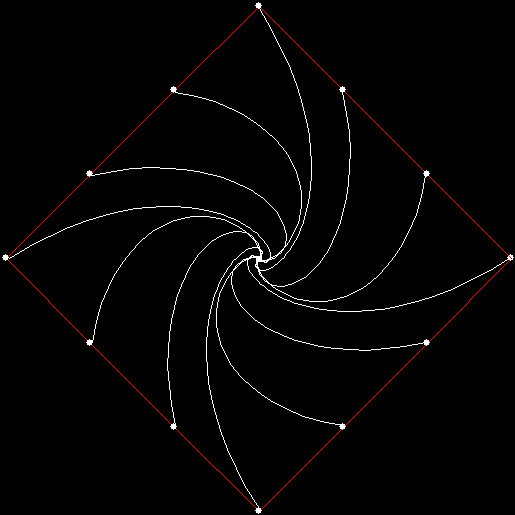
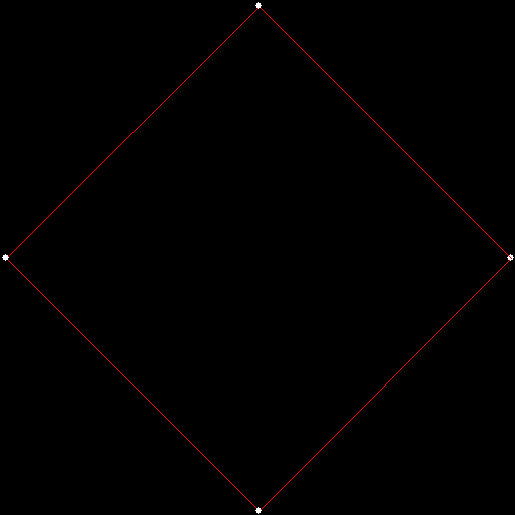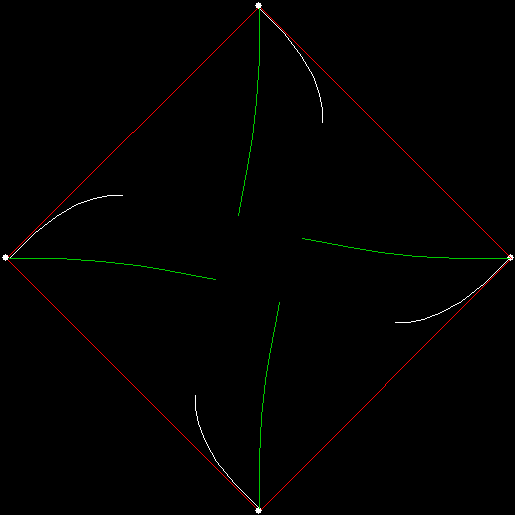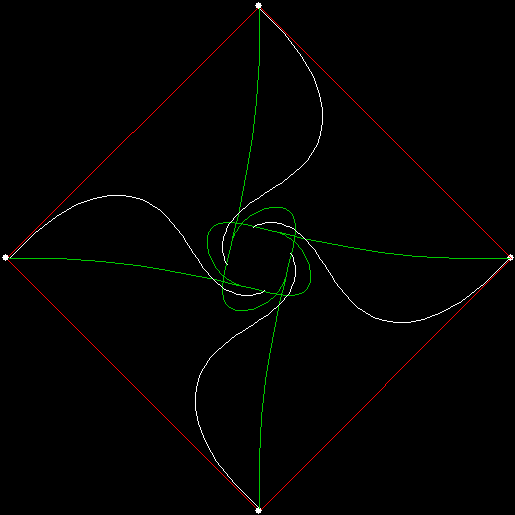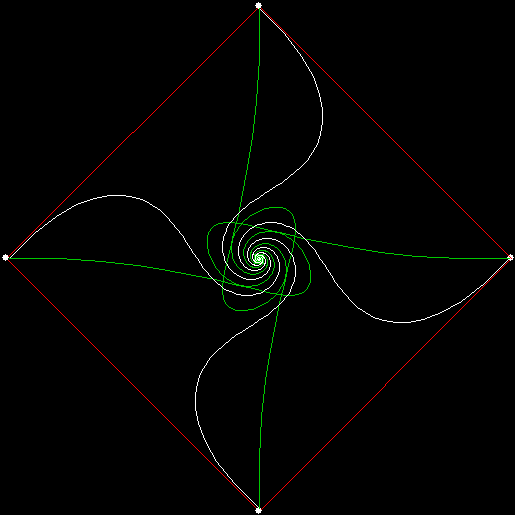
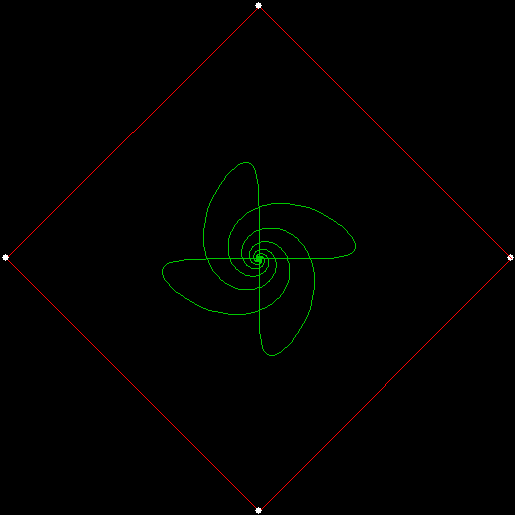
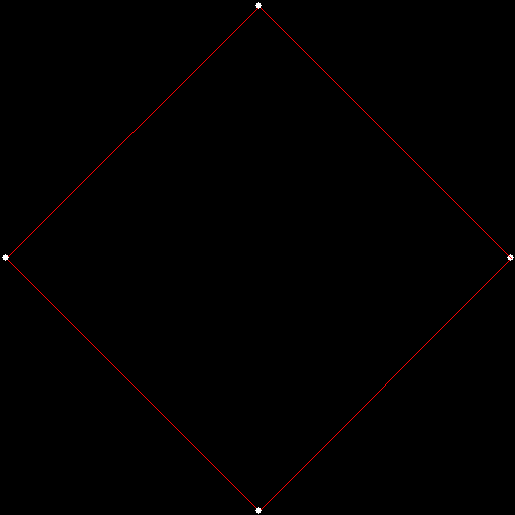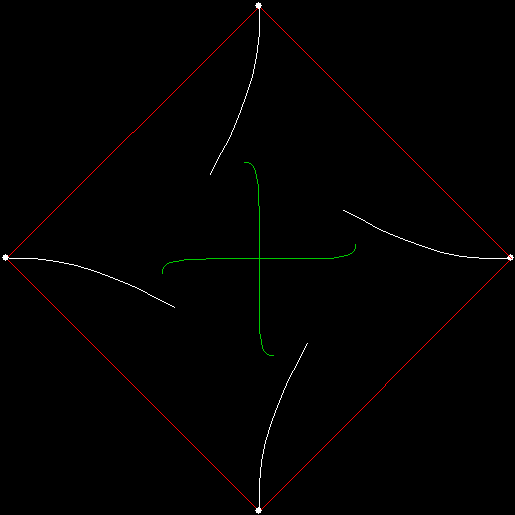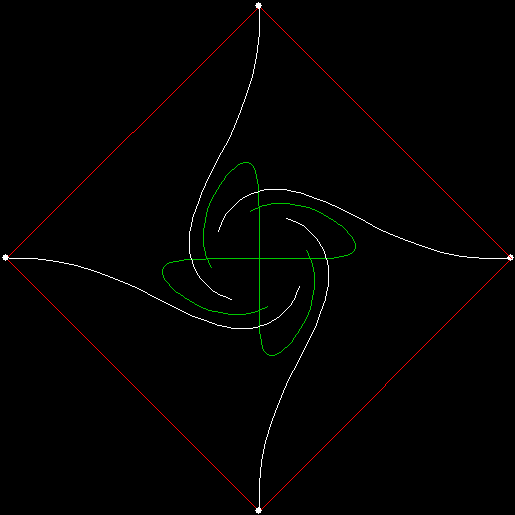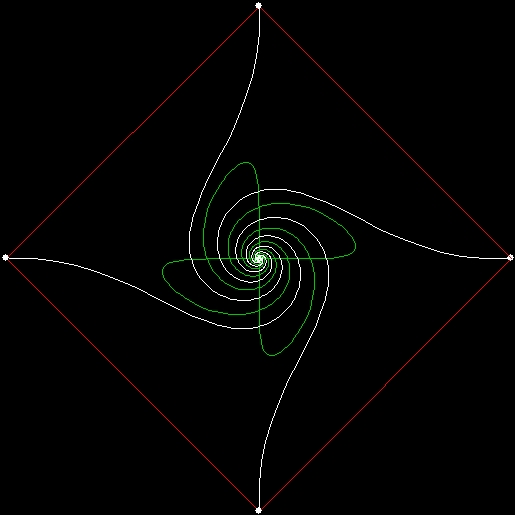
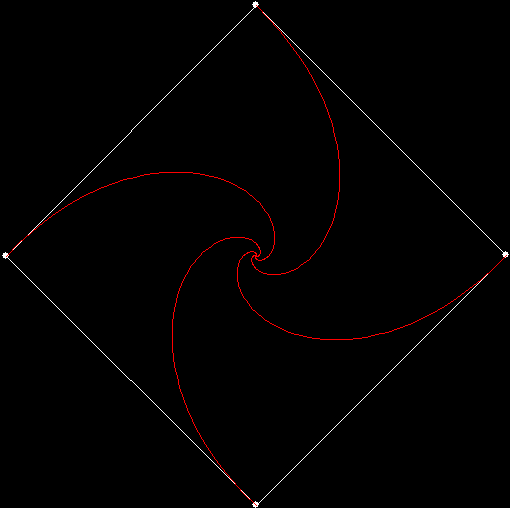
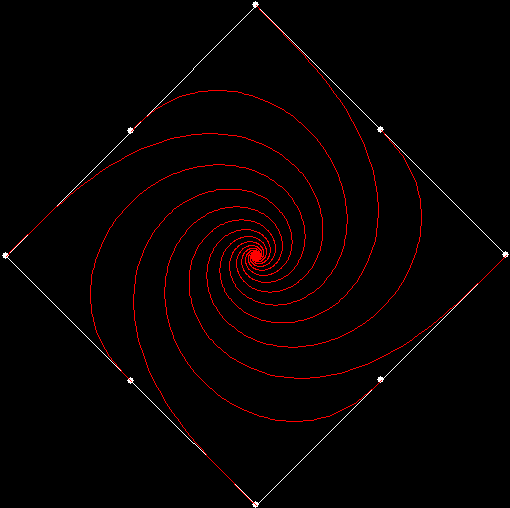
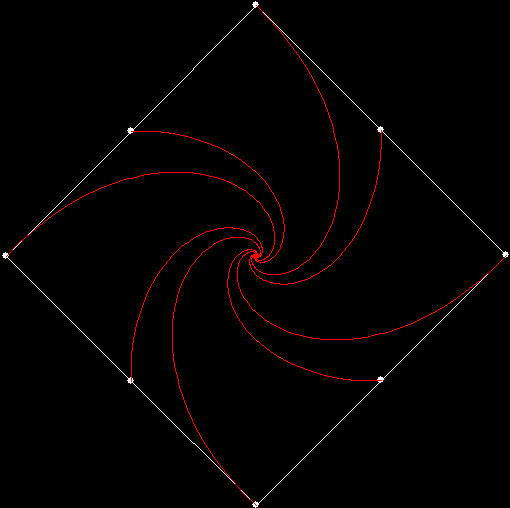
Twice before on Overlord-in-terms-of-Core-Issues-around-Maximal-Engagement-with-Key-Notions-of-the-Über-Feral, I’ve interrogated issues around pursuit curves. Imagine four mice or four beetles each sitting on one corner of a square and looking towards the centre of the square. If each mouse or beetle begins to run towards the mouse or beetle to its left, it will follow a curving path that takes it to the centre of the square, like this:

vertices = 4, pursuit = +1

The paths followed by the mice or beetles are pursuit curves. If you arrange eight mice clockwise around a square, with a mouse on each corner and a mouse midway along each side, you get a different set of pursuit curves:

v = 4 + 1 on the side, p = +1

Here each mouse is pursuing the mouse two places to its left:

v = 4+s1, p = +2

And here each mouse is pursuing the mouse three places to its left:

v = 4+s1, p = +3

Now try a different arrangement of the mice. In the square below, the mice are arranged clockwise in rows from the bottom right-hand corner. That is, mouse #1 begins on the bottom left-hand corner, mouse #2 begins between that corner and the centre, mouse #3 begins on the bottom left-hand corner, and so on. When each mice runs towards the mouse three places away, these pursuit curves appear:

v = 4 + 1 internally, p = +3

Here are some more:

v = 4 + i1, p = +5

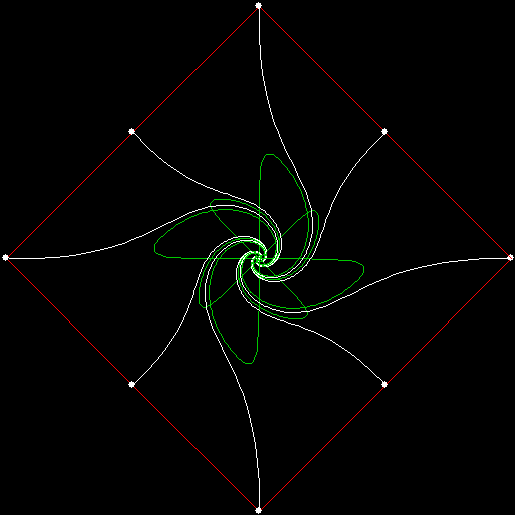
v = 4 + i2, p = +1

v = 4 + i2, p = +2

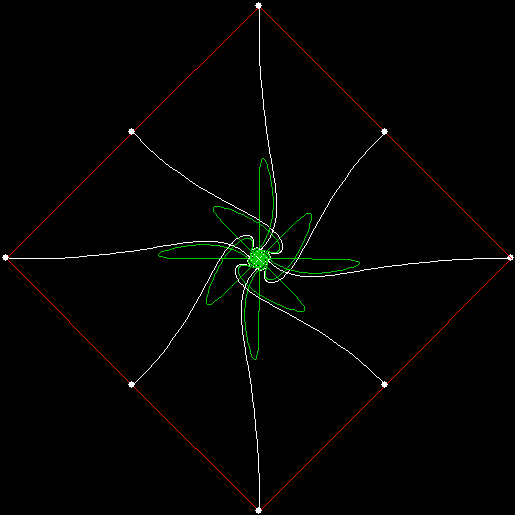
So far, all the mice have eventually run to the centre of the square, but that doesn’t happen here:

v = 4 + i2, p = 4

Here are more pursuit curves for the v4+i2 mice, using an animated gif:

v = 4 + i2, p = various (animated — open in new tab for clearer image)

And here are more pursuit curves that don’t end in the centre of the square:

v = 4 + i4, p = 4

v = 4 + i4, p = 8

v = 4 + i4, p = 12

v = 4 + i4, p = 16

But the v4+i4 pursuit curves more usually look like this:

v = 4 + i4, p = 7

Now try adapting the rules so that mice don’t run directly towards another mouse, but towards the point midway between two other mice. In this square, the odd- and even-numbered mice follow different rules. Mice #1, #3, #5 and #7 run towards the point midway between the mice one and two places away, while ice #2, #4, #6 and #8 run towards the point midway between the mice two and seven places away:

v = 4 + s1, p(1,3,5,7) = 1,2, p(2,4,6,8) = 2,7

I think the curves are very elegant. Here’s a slight variation:

v = 4 + s1, p1 = 1,3, p2 = 2,7

Now try solid curves:

v = 4 + s1, p1 = 1,3, p2 = 2,7 (red)

v = 4 + s1, p1 = 1,3, p2 = 2,7 (yellow-and-blue)

And some variants:

v = 4 + s1, p1 = 1,7, p2 = 1,2

v = 4 + s1, p1 = 2,3, p2 = 2,5

v = 4 + s1, p1 = 5,6, p2 = 1,3

v = 4 + s1, p1 = 5,6, p2 = 1,4

v = 4 + s1, p1 = 5,6, p2 = 1,6

Elsewhere other-posted:

• Polymorphous Pursuit
• Persecution Complex

Polymorphous Pursuit

by in Geometry, Mathematics, Pursuit Curves and tagged , , , , , , , , , , , , , , , , , , , , , | 2 Comments

Suppose four mice are standing on the corners of a large square. Each mouse begins running at the same speed towards the mouse one place away, reckoning clockwise. The mice will meet at the centre of the square and the path taken by each mouse will be what is known as a pursuit curve:

v4_mi1

vertices = 4, mouse-increment = 1

v4_mi1_animated

v = 4, mi = 1 (animated)

As I showed in “Persecution Complex”, it’s easy to find variants on the basic pursuit curve. If mi = 2, i.e. each mouse runs towards the mouse two places away, the mice will run in straight lines direct to the centre of the square:

v4_mi2

v = 4, mi = 2

v4_mi2_animated

v = 4, mi = 2 (animated)

That variant is trivial, but suppose there are eight mice, four starting on the corners of the square and four starting on the midpoints of the sides. Mice starting on the corners will run different pursuit curves to those starting on the midpoints, because the corners are further from the centre than the midpoints are:

v4_si1_mi1

v = 4, si = 1, mi = 1

v4_si1_mi1_extra

If mi = 3, the pursuit curves look like this:

v4_si1_mi3

v = 4, si = 1, mi = 3

v4_si1_mi3_animated

v = 4, si = 1, mi = 3 (animated)

Suppose there are twelve mice, four on each corner and two more on each side. If each mouse runs towards the mouse four places away, then the pursuit curves don’t all meet in the centre of the square. Instead, they meet in groups of three at four points equidistant from the centre, like this:

v4_si2_mi4

v4_si2_mi4_curves

v = 4, si = 2, mi = 4

v4_si2_mi4_animated

v = 4, si = 2, mi = 4 (animated)

v4_si4_mi4_animated

v = 4, si = 4, mi = 4 (animated)

v4_si4_mi4_large

v = 4, si = 4, mi = 4 (zoom)

Now suppose each mouse become sophisticated and runs toward the combined positions of two other mice, one two places away, the other three places away, like this:

v4_si1_mi2_3

v = 4, si = 1, mi = (2, 3)

v4_si1_mi2_3_animated

v = 4, si = 1, mi = (2, 3) (animated)

These polypursuits, as they could be called, can have complicated central regions:

v4_si2_mi1_4

v = 4, si = 2, mi = (1, 4)

v4_si2_mi1_4_animated

v = 4, si = 2, mi = (1, 4) (animated)

v4_si_va_mi_va

v = 4, si = various, mi = various

And what if you have two teams of mice, running towards one or more mice on the other team? For example, suppose two mice, one from each team, start on each corner of a square. Each mouse on team 1 runs towards the mouse on team 2 that is one place away, while each mouse on team 2 runs towards the mouse on team 1 that is two places away. If the pursuits curves of team 1 are represented in white and the pursuit curves of team 2 in green, the curves look like this:

2v4_mi1_mi2

v = 4 * 2, vmi = 1, vmi = 2

2v4_mi1_mi2_green

v = 4 * 2, vmi = 1, vmi = 2

2v4_mi1_mi2_animated

v = 4 * 2, vmi = 1, vmi = 2 (animated)

Now suppose the four mice of team 1 start on the corners while the mice of team 2 start at the centre of the square.

v4_c4_vmi1_cmi2_white

v = 4, centre = 4, vmi = 1, cmi = 2 (white team)

v4_c4_vmi1_cmi2_green

v = 4, centre = 4, vmi = 1, cmi = 2 (green team)

v4_c4_vmi1_cmi2_both

v = 4, centre = 4, vmi = 1, cmi = 2 (both teams)

v4_c4_vmi1_cmi2_animated

v = 4, centre = 4, vmi = 1, cmi = 2 (animated)

Here are more variants on pursuit curves formed by two teams of mice, one starting on the corners, one at the centre:

v4_c4_vmi0_1_cmi0

v = 4, centre = 4, vmi = (0, 1), cmi = 0

v4_c4_vmi0_2_cmi0

v = 4, centre = 4, vmi = (0, 2), cmi = 0

v4_c4_vmi0_3_cmi0

v = 4, centre = 4, vmi = (0, 3), cmi = 0

2v4_mi1_mi2_both

Persecution Complex

by in Geometry, Mathematics, Pursuit Curves and tagged , , , , , , , , , , , , , , , , , , , , , , | Leave a comment

Imagine four mice sitting on the corners of a square. Each mouse begins to run towards its clockwise neighbour. What happens? This:

Four mice chasing each other

Four mice chasing each other

The mice spiral to the centre and meet, creating what are called pursuit curves. Now imagine eight mice on a square, four sitting on the corners, four sitting on the midpoints of the sides. Each mouse begins to run towards its clockwise neighbour. Now what happens? This:

Eight mice chasing each other

Eight mice chasing each other

But what happens if each of the eight mice begins to run towards its neighbour-but-one? Or its neighbour-but-two? And so on. The curves begin to get more complex:

square+midpoint+2

(Please open the following image in a new window if it fails to animate.)

square+midpoint+3

You can also make the mice run at different speeds or towards neighbours displaced by different amounts. As these variables change, so do the patterns traced by the mice:

• Continue reading Persecution Complexified