Category Archives: Square Roots

Tright Sights

by in Circles, Fractals, Geometry, Mathematics, Square Roots, Triangles and tagged , , , , , , | Leave a comment

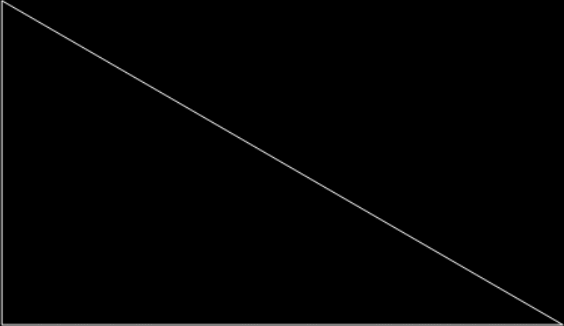
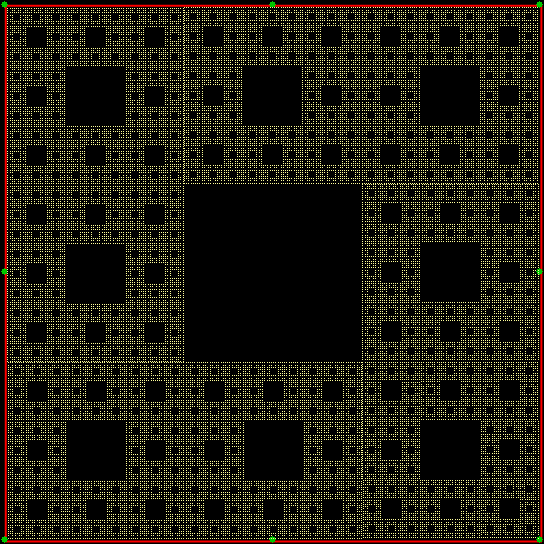
Here’s a right triangle, where a^2 + b^2 = c^2. But what are the exact values of a, b, and c?

You might be able to guess by eye, but could you prove your guess? Now try the same right triangle tiled with three identical copies of itself:

1-√3-2 triangle as rep3 rep-tile

Now you can prove the exact values of a, b, and c. If the vertical side, a, is 1, then the hypotenuse, c, is 2, because the length that fits once into a fits twice into c. Therefore 2^2 = 1^2 + b^2 → 4 = 1 + b^2 → 4-1 = b^2 → 3 = b^2 → √3 = b. The horizontal side, b, has a length of √3 = 1.73205080757… So the right triangle is 1-√3-2. And if it’s rep3, that is, can be divided into three identical copies of itself, then it’s also rep9, rep27, and so on:

1-√3-2 triangle as rep9 rep-tile

1-√3-2 triangle as rep27 rep-tile

1-√3-2 triangle as rep81 rep-tile

1-√3-2 triangle as rep243 rep-tile

1-√3-2 triangle as rep729 rep-tile

Once you’ve got a rep-tile, you can create fractals. But the 1-√3-2 triangle is cramped. You need more space to work with. And it’s easy to find that space when you realize that a standard equilateral triangle can be divided into six 1-√3-2 triangles:

Equilateral triangle divided into six 1-√3-2 triangles

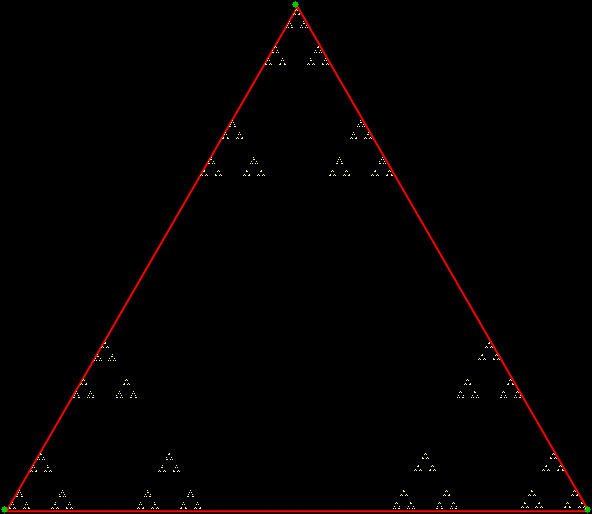
Equilateral triangle tiled with 1-√3-2 triangles (stage 1)

(please open in new window if image is distorted)

Equilateral triangle tiled with 1-√3-2 triangles (stage 2)

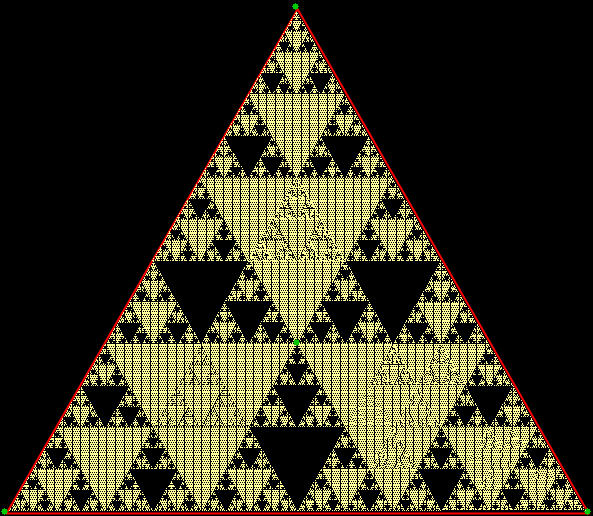
Equilateral triangle tiled with 1-√3-2 triangles (stage 3)

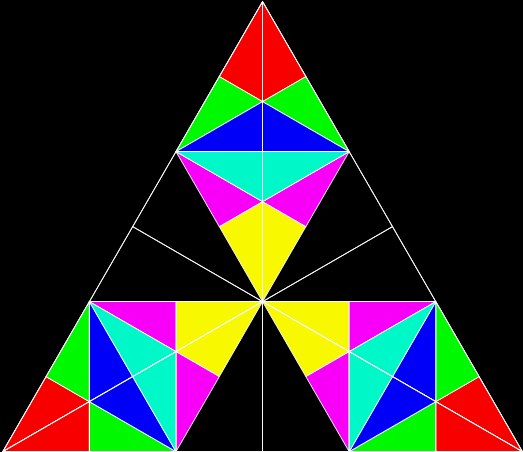
Here are variant colorings of the stage-3 tiled triangle:

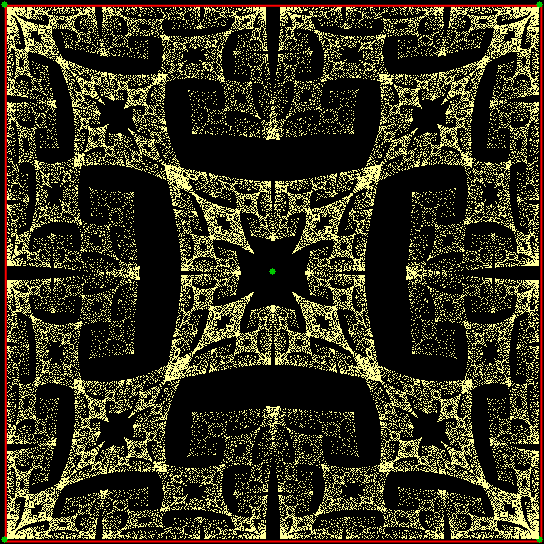
But where are the fractals? In one way, you’ve already seen them. But they get more obvious like this:

Fractal stage 1

Fractal #2

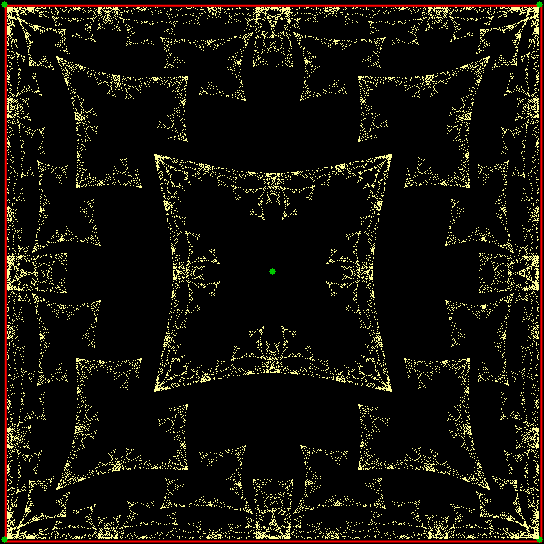
Fractal #3

Fractal #4

Fractal #5

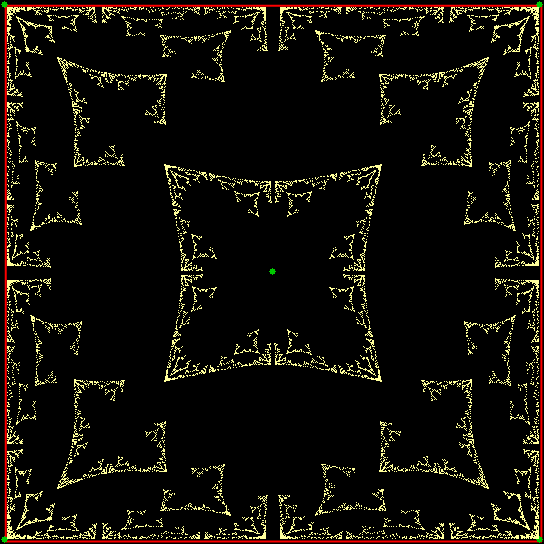
Fractal #6

Fractal #7

Fractal #8

Fractal (animated)

Another fractal stage 1

[…]

↓

[…]

Another fractal #8

Another fractal (animated)

And when you have a fractal created using an equilateral triangle, it’s easy to expand the fractal into a circle, like this:

Original fractal

↓

Fractal expanded into circle

Triangular fractal to circular fractal (animated)

Root Pursuit

by in √2, Base Behavior, Integer sequences, Irrational numbers, Mathematics, Powers, Square root of 2, Square Roots and tagged , , , , , , , , , , , , , , , , , , | Leave a comment

Roots are hard, powers are easy. For example, the square root of 2, or √2, is the mysterious and never-ending number that is equal to 2 when multiplied by itself:

• √2 = 1·414213562373095048801688724209698078569671875376948073...

It’s hard to calculate √2. But the powers of 2, or 2^p, are the straightforward numbers that you get by multiplying 2 repeatedly by itself. It’s easy to calculate 2^p:

• 2 = 2^1
• 4 = 2^2
• 8 = 2^3
• 16 = 2^4
• 32 = 2^5
• 64 = 2^6
• 128 = 2^7
• 256 = 2^8
• 512 = 2^9
• 1024 = 2^10
• 2048 = 2^11
• 4096 = 2^12
• 8192 = 2^13
• 16384 = 2^14
• 32768 = 2^15
• 65536 = 2^16
• 131072 = 2^17
• 262144 = 2^18
• 524288 = 2^19
• 1048576 = 2^20
[...]

But there is a way to find √2 by finding 2^p, as I discovered after I asked a simple question about 2^p and 3^p. What are the longest runs of matching digits at the beginning of each power?

• 131072 = 2^17
• 129140163 = 3^17
• 1255420347077336152767157884641... = 2^193
• 1214512980685298442335534165687... = 3^193
• 2175541218577478036232553294038... = 2^619
• 2177993962169082260270654106078... = 3^619
• 7524389324549354450012295667238... = 2^2016
• 7524012611682575322123383229826... = 3^2016

There’s no obvious pattern. Then I asked the same question about 2^p and 5^p. And an interesting pattern appeared:

• 32 = 2^5
• 3125 = 5^5
• 316912650057057350374175801344 = 2^98
• 3155443620884047221646914261131... = 5^98
• 3162535207926728411757739792483... = 2^1068
• 3162020133383977882730040274356... = 5^1068
• 3162266908803418110961625404267... = 2^127185
• 3162288411569894029343799063611... = 5^127185

The digits 31622 rang a bell. Isn’t that the start of √10? Yes, it is:

• √10 = 3·1622776601683793319988935444327185337195551393252168268575...

I wrote a fast machine-code program to find even longer runs of matching initial digits. Sure enough, the pattern continued:

• 316227... = 2^2728361
• 316227... = 5^2728361
• 3162277... = 2^15917834
• 3162277... = 5^15917834
• 31622776... = 2^73482154
• 31622776... = 5^73482154
• 3162277660... = 2^961700165
• 3162277660... = 5^961700165

But why are powers of 2 and 5 generating the digits of √10? If you’re good at math, that’s a trivial question about a trivial discovery. Here’s the answer: We use base ten and 10 = 2 * 5, 10^2 = 100 = 2^2 * 5^2 = 4 * 25, 10^3 = 1000 = 2^3 * 5^3 = 8 * 125, and so on. When the initial digits of 2^p and 5^p match, those matching digits must come from the digits of √10. Otherwise the product of 2^p * 5^p would be too large or too small. Here are the records for matching initial digits multiplied by themselves:

• 32 = 2^5
• 3125 = 5^5
• 3^2 = 9

• 316912650057057350374175801344 = 2^98
• 3155443620884047221646914261131... = 5^98
• 31^2 = 961

• 3162535207926728411757739792483... = 2^1068
• 3162020133383977882730040274356... = 5^1068
• 3162^2 = 9998244

• 3162266908803418110961625404267... = 2^127185
• 3162288411569894029343799063611... = 5^127185
• 31622^2 = 999950884

• 316227... = 2^2728361
• 316227... = 5^2728361
• 316227^2 = 99999515529

• 3162277... = 2^15917834
• 3162277... = 5^15917834
• 3162277^2 = 9999995824729

• 31622776... = 2^73482154
• 31622776... = 5^73482154
• 31622776^2 = 999999961946176

• 3162277660... = 2^961700165
• 3162277660... = 5^961700165
• 3162277660^2 = 9999999998935075600

The square of each matching run falls short of 10^p. And so when the digits of 2^p and 5^p stop matching, one power must fall below √10, as it were, and one must rise above:

• 3 162266908803418110961625404267... = 2^127185
• 3·162277660168379331998893544432... = √10
• 3 162288411569894029343799063611... = 5^127185

In this way, 2^p * 5^p = 10^p. And that’s why matching initial digits of 2^p and 5^p generate the digits of √10. The same thing, mutatis mutandis, happens in base 6 with 2^p and 3^p, because 6 = 2 * 3:

• 2.24103122055214532500432040411... = √6 (in base 6)

• 24 = 2^4
• 213 = 3^4
• 225522024 = 2^34 in base 6 = 2^22 in base 10
• 22225525003213 = 3^34 (3^22)
• 2241525132535231233233555114533... = 2^1303 (2^327)
• 2240133444421105112410441102423... = 3^1303 (3^327)
• 2241055222343212030022044325420... = 2^153251 (2^15007)
• 2241003215453455515322105001310... = 3^153251 (3^15007)
• 2241032233315203525544525150530... = 2^233204 (2^20164)
• 2241030204225410320250422435321... = 3^233204 (3^20164)
• 2241031334114245140003252435303... = 2^2110415 (2^102539)
• 2241031103430053425141014505442... = 3^2110415 (3^102539)

And in base 30, where 30 = 2 * 3 * 5, you can find the digits of √30 in three different ways, because 30 = 2 * 15 = 3 * 10 = 5 * 6:

• 5·E9F2LE6BBPBF0F52B7385PE6E5CLN... = √30 (in base 30)

• 55AA4 = 2^M in base 30 = 2^22 in base 10
• 5NO6CQN69C3Q0E1Q7F = F^M = 15^22
• 5E63NMOAO4JPQD6996F3HPLIMLIRL6F... = 2^K6 (2^606)
• 5ECQDMIOCIAIR0DGJ4O4H8EN10AQ2GR... = F^K6 (15^606)
• 5E9DTE7BO41HIQDDO0NB1MFNEE4QJRF... = 2^B14 (2^9934)
• 5E9G5SL7KBNKFLKSG89J9J9NT17KHHO... = F^B14 (15^9934)
[...]
• 5R4C9 = 3^E in base 30 = 3^14 in base 10
• 52CE6A3L3A = A^E = 10^14
• 5E6SOQE5II5A8IRCH9HFBGO7835KL8A = 3^3N (3^113)
• 5EC1BLQHNJLTGD00SLBEDQ73AH465E3... = A^3N (10^113)
• 5E9FI455MQI4KOJM0HSBP3GG6OL9T8P... = 3^EJH (3^13187)
• 5E9EH8N8D9TR1AH48MT7OR3MHAGFNFQ... = A^EJH (10^13187)
[...]
• 5OCNCNRAP = 5^I in base 30 = 5^18 in base 10
• 54NO22GI76 = 6^I (6^18)
• 5EG4RAMD1IGGHQ8QS2QR0S0EH09DK16... = 5^1M7 (5^1567)
• 5E2PG4Q2G63DOBIJ54E4O035Q9TEJGH... = 6^1M7 (6^1567)
• 5E96DB9T6TBIM1FCCK8A8J7IDRCTM71... = 5^F9G (5^13786)
• 5E9NM222PN9Q9TEFTJ94261NRBB8FCH... = 6^F9G (6^13786)
[...]

So that’s √10, √6 and √30. But I said at the beginning that you can find √2 by finding 2^p. How do you do that? By offsetting the powers, as it were. With 2^p and 5^p, you can find the digits of √10. With 2^(p+1) and 5^p, you can find the digits of √2 and √20, because 2^(p+1) * 5^p = 2 * 2^p * 5^p = 2 * 10^p:

•  √2 = 1·414213562373095048801688724209698078569671875376948073...
• √20 = 4·472135954999579392818347337462552470881236719223051448...

• 16 = 2^4
• 125 = 5^3
• 140737488355328 = 2^47
• 142108547152020037174224853515625 = 5^46
• 1413... = 2^243
• 1414... = 5^242
• 14141... = 2^6651
• 14142... = 5^6650
• 141421... = 2^35389
• 141420... = 5^35388
• 4472136... = 2^162574
• 4472135... = 5^162573
• 141421359... = 2^3216082
• 141421352... = 5^3216081
• 447213595... = 2^172530387
• 447213595... = 5^172530386
[...]

La Formule de François

by in √2, Infinity, Irrational numbers, π, Mathematics, Pi, Square root of 2, Square Roots and tagged , , , , , , | Leave a comment

Here is a beautiful and astonishingly simple formula for π created by the French mathematician François Viète (1540-1603):

• 2 / π = √2/2 * √(2 + √2)/2 * √(2 + √(2 + √2))/2…

I can remember testing the formula on a scientific calculator that allowed simple programming. As I pressed the = key and the results began to home in on π, I felt as though I was watching a tall and elegant temple emerge through swirling mist.

Triangular Squares

by in √2, Integer sequences, Irrational numbers, Mathematics, Square root of 2, Square Roots, Squares, Triangular Numbers and tagged , , , , , , , , , , , , , | Leave a comment

The numbers that are both square and triangular are beautifully related to the best approximations to √2:

Number

Square Root

Factors of root
1 1 1
36 6 2 * 3
1225 35 5 * 7
41616 204 12 * 17

and so on.

In each case the factors of the root are the numerator and denominator of the next approximation to √2. — David Wells, The Penguin Dictionary of Curious and Interesting Mathematics (1986), entry for “36”.

Elsewhere other-accessible

• A001110 — Square triangular numbers: numbers that are both triangular and square

The Trivial Troot

by in √2, Integer sequences, Irrational numbers, Mathematics, Square root of 2, Square Roots, Triangular Numbers and tagged , , , , , , , , , , , , , , | Leave a comment

Here is the square root of 2:

√2 = 1·414213562373095048801688724209698078569671875376948073176679738...

Here is the square root of 20:

√20 = 4·472135954999579392818347337462552470881236719223051448541794491...

And here are the first few triangular numbers:

1, 3, 6, 10, 15, 21, 28, 36, 45, 55, 66, 78, 91, 105, 120, 136, 153, 171, 190, 210, 231, 253, 276, 300, 325, 351, 378, 406, 435, 465, 496, 528, 561, 595, 630, 666, 703, 741, 780, 820, 861, 903, 946, 990, 1035...

What links √2 and √20 strongly with the triangular numbers? At first glance, nothing does. The square roots of 2 and 20 are very different from the triangular numbers. Square roots like those are irrational, that is, they can’t be represented as a fraction or ratio of integers. This means that their digits go on for ever, never falling into a regular pattern. So the digits are hard to calculate. The sequence of triangular numbers also goes on for ever, but it’s very easy to calculate. The triangular numbers get their name from the way they can be arranged into simple triangles, like this:

* = 1

*
** = 3

*
**
*** = 6

*
**
***
**** = 10

*
**
***
****
***** = 15

The 1st triangular number is 1, the 2nd is 3 = 1+2, the 3rd is 6 = 1+2+3, the 4th is 10 = 1+2+3+4, and so on. The n-th triangular number = 1+2+3…+n, so the formula for the n-th triangular number is n*(n+1)/2 = (n^2+n)/2. So what’s the 123456789th triangular number? Easy: it’s 7620789436823655 (see A077694 at the OEIS). But what’s the 123456789th digit of √2 or √20? That’s not easy to answer. But here’s something else that is easy to answer. If tri(n) is the n-th triangular number, what are the values of n when tri(n) is one digit longer than tri(n-1)? That is, what are the values of n when tri(n) increases in length by one digit? If you look at the beginning of the sequence, you can see the first three answers:

1, 3, 6, 10, 15, 21, 28, 36, 45, 55, 66, 78, 91, 105...

1 is one digit longer than nothing, as it were, and 1 = tri(1); 10 is one digit longer than 6 and 10 = tri(4); 105 is one digit longer than 91 and 105 = tri(14). Here are some more answers, giving triangular numbers on the left, as they increase in length by one digit, and the n of tri(n) on the right:

1 ← 1
10 ← 4
105 ← 14
1035 ← 45
10011 ← 141
100128 ← 447
1000405 ← 1414
10001628 ← 4472
100005153 ← 14142
1000006281 ← 44721
10000020331 ← 141421
100000404505 ← 447214
1000001326005 ← 1414214
10000002437316 ← 4472136
100000012392316 ← 14142136
1000000042485480 ← 44721360
10000000037150046 ← 141421356
100000000000018810 ← 447213595
1000000000179470703 ← 1414213562
10000000002237948990 ← 4472135955
100000000010876002500 ← 14142135624
1000000000022548781025 ← 44721359550
10000000000026940078203 ← 141421356237
100000000000242416922750 ← 447213595500
1000000000000572687476751 ← 1414213562373
10000000000004117080477500 ← 4472135955000
100000000000007771272992046 ← 14142135623731
1000000000000031576491575006 ← 44721359549996
10000000000000140731196136705 ← 141421356237310
100000000000000250760786750861 ← 447213595499958
1000000000000000638090771126060 ← 1414213562373095
10000000000000000479330922588410 ← 4472135954999579
100000000000000000169466805816725 ← 14142135623730950
1000000000000000025572412483843115 ← 44721359549995794
10000000000000000087657358700327265 ← 141421356237309505
100000000000000000097566473134542830 ← 447213595499957939
1000000000000000000987561276980703725 ← 1414213562373095049
10000000000000000003048443380954913921 ← 4472135954999579393
100000000000000000006832246143819194316 ← 14142135623730950488
1000000000000000000014155501020518731556 ← 44721359549995793928

Can you spot the patterns? When tri(n) has an odd number of digits, n approximates the digits of √2; when tri(n) has an even number of digits, n approximates the digits of √20. And what can you call the approximations? Well, in a way they’re triangular roots so I’m calling them troots. Here are the troots for tri(n) with an odd number of digits:

1 → 1
14 → 105
141 → 10011
1414 → 1000405
14142 → 100005153
141421 → 10000020331
1414214 → 1000001326005
14142136 → 100000012392316
141421356 → 10000000037150046
1414213562 → 1000000000179470703
14142135624 → 100000000010876002500
141421356237 → 10000000000026940078203
1414213562373 → 1000000000000572687476751
14142135623731 → 100000000000007771272992046
141421356237310 → 10000000000000140731196136705
1414213562373095 → 1000000000000000638090771126060
14142135623730950 → 100000000000000000169466805816725
141421356237309505 → 10000000000000000087657358700327265
1414213562373095049 → 1000000000000000000987561276980703725
14142135623730950488 → 100000000000000000006832246143819194316
14142135623730950488... = √2 (without the decimal point)

When I first found these patterns, I thought I might have discovered something mathematically profound. I hadn’t. Troots are trivial. I think troots are beautiful too, but a little thought soon showed me how easily and obviously they arise. Remember that the formula for tri(n), the n-th triangular number, is tri(n) = (n^2+n)/2. As you can see above, when tri(n) is increasing in length by one digit, it rises above the next power of 10, which always begins with 1 followed by only 0s. Therefore n^2+n will begin with the digit 2 followed by some 0s, which then becomes 1 followed by some 0s as (n^2+n) is divided by 2. So n for tri(n) increasing-by-one-digit will be the first integer, n, where n^2+n yields a number with 2 as the leading digit followed by more and more 0s.

And that’s why n approximates the digits of √2·0000… and √20·0000…, for tri(n) with an odd and even number of digits, respectively. Similar trootful patterns exist in other bases and for other polygonal numbers, like the square numbers, the pentagonal numbers and so on. The troots are beautiful to see but trivial to explain. All the same, there is a sense in which you can say the mindless sequence of triangular numbers is “calculating” the digits of √2 and √20. It even rounds up the final digits when necessary:

1414214 → 1000001326005
14142136 → 100000012392316
141421356 → 10000000037150046
141421356... = √2
[...]
14142135624 → 100000000010876002500
141421356237 → 10000000000026940078203
141421356237... = √2
[...]
14142135623731 → 100000000000007771272992046
141421356237310 → 10000000000000140731196136705
1414213562373095 → 1000000000000000638090771126060
1414213562373095... = √2
[...]
1414213562373095049 → 1000000000000000000987561276980703725
14142135623730950488 → 100000000000000000006832246143819194316
14142135623730950488... = √2

The Power of Powder

by in √2, French, Infinity, Irrational numbers, Mathematics, Square root of 2, Square Roots and tagged , , , , , , , , , , , , , , , , , , | Leave a comment

• Racine carrée de 2, c’est 1,414 et des poussières… Et quelles poussières ! Des grains de sable qui empêchent d’écrire racine de 2 comme une fraction. Autrement dit, cette racine n’est pas dans Q. — Rationnel mon Q: 65 exercices de styles, Ludmilla Duchêne et Agnès Leblanc (2010)

• The square root of 2 is 1·414 and dust… And what dust! Grains of sand that stop you writing the root of 2 as a fraction. Put another way, this root isn’t in Q [the set of rational numbers].

Root Routes

by in Chaos Game, Fractals, Geometry, Mathematics, Square Roots, Squares, Triangles and tagged , , , , , , , , , , , , , , | Leave a comment

Suppose a point traces all possible routes jumping half-way towards the three vertices of an equilateral triangle. A special kind of shape appears — a fractal called the Sierpiński triangle that contains copies of itself at smaller and smaller scales:

Sierpiński triangle, jump = 1/2

And what if the point jumps 2/3rds of the way towards the vertices as it traces all possible routes? You get this dull fractal:

Triangle, jump = 2/3

But if you add targets midway along each side of the triangle, you get this fractal with the 2/3rds jump:

Triangle, jump = 2/3, side-targets

Now try the 1/2-jump triangle with a target at the center of the triangle:

Triangle, jump = 1/2, central target

And the 2/3-jump triangle with side-targets and a central target:

Triangle, jump = 2/3, side-targets, central target

But why stop at simple jumps like 1/2 and 2/3? Let’s take the distance to the target, td, and use the function 1-(sqrt(td/7r)), where sqrt() is the square-root and 7r is 7 times the radius of the circumscribing circle:

Triangle, jump = 1-(sqrt(td/7r))

Here’s the same jump with a central target:

Triangle, jump = 1-(sqrt(td/7r)), central target

Now let’s try squares with various kinds of jump. A square with a 1/2-jump fills evenly with points:

Square, jump = 1/2 (animated)

The 2/3-jump does better with a central target:

Square, jump = 2/3, central target

Or with side-targets:

Square, jump = 2/3, side-targets

Now try some more complicated jumps:

Square, jump = 1-sqrt(td/7r)

Square, jump = 1-sqrt(td/15r), side-targets

And what if you ban the point from jumping twice or more towards the same target? You get this fractal:

Square, jump = 1-sqrt(td/6r), ban = prev+0

Now try a ban on jumping towards the target two places clockwise of the previous target:

Square, jump = 1-sqrt(td/6r), ban = prev+2

And the two-place ban with a central target:

Square, jump = 1-sqrt(td/6r), ban = prev+2, central target

And so on:

Square, jump = 1-sqrt(td/6.93r), ban = prev+2, central target

Square, jump = 1-sqrt(td/7r), ban = prev+2, central target

These fractals take account of the previous jump and the pre-previous jump:

Square, jump = 1-sqrt(td/4r), ban = prev+2,2, central target

Square, jump = 1-sqrt(td/5r), ban = prev+2,2, central target

Square, jump = 1-sqrt(td/6r), ban = prev+2,2, central target

Elsewhere other-accessible

• Boole(b)an #2 — fractals created in similar ways

Squooh You

by in Mathematics, Square Roots and tagged , , , , , , , , , , , , , | Leave a comment

Here’s an interesting little puzzle:

Winnie-the-Pooh and Piglet set out to visit one another. They leave their houses at the same time and walk along the same road. But Piglet is absorbed in counting the birds overhead, and Winnie-the-Pooh is composing a new “hum,” so they pass one another without noticing. One minute after the meeting, Winnie-the-Pooh is at Piglet’s house, and 4 minutes after the meeting Piglet is at Winnie-the-Pooh’s. How long has each of them walked? — “A puzzle by S. Sefibekov” viâ Futility Closet

If you’re good at maths, you should see the answer in an intuitive instant. I’m not good at maths, so it took me much longer, because I didn’t understand what was going on. But I can explain the answer like this. Pooh is obviously walking faster than Piglet. Therefore, Pooh and Piglet can’t have met after one minute, because that would mean Pooh takes one minute to walk the distance walked by Piglet in one minute.

So let’s suppose Pooh and Piglet met after two minutes. If Pooh takes one minute to walk the distance walked by Piglet in two minutes, then Pooh is walking twice as fast as Piglet. Does that work? Yes, because Piglet walks Pooh’s distance in four minutes, which is twice as long as Pooh took. Therefore Piglet is walking twice as slowly as Pooh. It’s symmetrical and we can conclude that they did indeed meet after two minutes. Pooh then walks another minute, for three minutes in total, and Piglet walks another four minutes, for six minutes in total.

But guessing is not a good way to find the answer to the puzzle. Let’s try to reason it through properly. Suppose that Pooh and Piglet meet after one unit of time, during which Piglet has walked one unit of distance and Pooh has walked x units of distance, where x > 1. In other words, Pooh is walking x times faster than Piglet. The distances they walk before meeting are therefore in the ratio:

1 : x

Next, note that Pooh will cover the distance Piglet has already walked in 1 unit / x = 1 minute, while Piglet covers the distance Pooh has already walked in x / 1 = 4 minutes. The times they take are therefore in the ratio:

1 / x : x → 1 : x^2 → 1 : 4

And if 1 : x^2 is 1 : 4 (the ratio of the minutes they walk after meeting), then 1 : x (the ratio of the distances they walk before meeting) = 1 : √(x^2) = 1 : √4 = 1 : 2. Pooh is therefore walking 2x faster than Piglet and Piglet is walking 2x slower than Pooh. If Pooh covers Piglet’s distance in 1 minute, Piglet must have taken 2 minutes to walk that distance. And if Piglet covers Pooh’s distance in 4 minutes, Pooh must have taken 2 minutes to walk that distance.

Therefore, when they meet, each of them has been walking for 2 minutes. Pooh therefore walks 2 + 1 = 3 minutes in total and Piglet walks 2 + 4 = 6 minutes in total.

The result can be generalized for all relative speeds. Suppose that Pooh and Piglet meet after m1 minutes and that Pooh then takes m2 minutes to walk the distance Piglet walked in m1 minutes, while Piglet takes m3 minutes to walk the distance Pooh walked in m1 minutes. The time they walk before they meet, m1 minutes, is therefore supplied by this simple equation:

m1 = √(m3 / m2)

And you can call √(m3 / m2), the square root of m3 / m2, the squooh function:

m1 = √(m3 / m2) = squooh(m2,m3)

Now suppose the distance between Pooh’s and Piglet’s houses houses is 12 units of distance and that Piglet always walks at 1 unit a minute. If Pooh walks at the same speed as Piglet, i.e. 1 unit a minute, then:

After they meet, Pooh walks 6 more min = m2, Piglet walks 6 more min = m3.

How long do they walk before they meet?

m1 = m3 / m2 = 1, √1 * 6 = 6

They meet after 6 min.

Now suppose that after they meet, Pooh walks 2 more min, Piglet walks 8 more min.

Therefore, m3 / m2 = 4, √4 * 2 = 2 * 2 = 4 = m1

Therefore they walk for 4 min before they meet and Pooh walks 2x faster than Piglet.

After they meet, Pooh walks 1 more min, Piglet walks 9 more min (m3 / m2 = 9, √9 * 1 = 3)

Therefore they walk for 3 min before they meet and Pooh walks 3x faster than Piglet.

After they meet, Pooh walks 0·6 more min, Piglet walks 9·6 more min (m3 / m2 = 16, √16 * 0·6 = 4 * 0·6 = 2·4)

Therefore they walk for 2·4 min before they meet and Pooh walks 4x faster than Piglet:

After they meet, Pooh walks 0·4 more min, Piglet walks 10 more min (m3 / m2 = 25, √25 * 0·4 = 5 * 0·4 = 2)

Therefore they walk for 2 min before they meet and Pooh walks 5x faster than Piglet.

And so on.