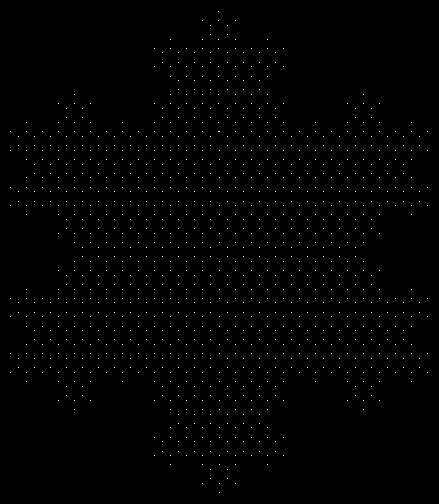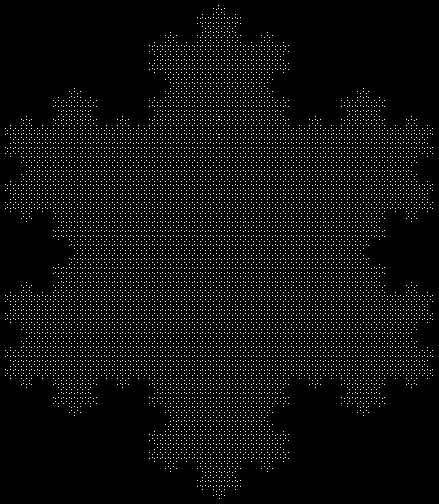Why stop at primes? Those are the numbers the Ulam spiral is usually used for. You get a grid of square blocks, then move outward from the middle of the grid in a spiral, counting as you go. If the count matches a prime, you fill the block in. The first block is 1. Not filled. The second block is 2, which is prime. So the block is filled. The third block is 3, which is prime. Filled again. And so on. In the end, the Ulam spiral for primes looks like this:

The Ulam spiral of prime numbers

But why stop at primes? If you change the fill-test, you get different patterns. I’ve recently tried a test based on how many ways a number can be represented as the sum of consecutive integers. For example, 5, 208 and 536 can be represented in only one way:

Let’s use “runsum” to mean a sum of consecutive integers. If the function runsum(n) returns the count of runsums for n, then runsum(5) = runsum(208) = runsum(536) = 1. Here are spirals for runsum(n) = 1:

A spiral for runsum(n) = 1, i.e. numbers that are the sum of consecutive integers in only one way

runsum(n) = 1 (higher resolution)

runsum(n) = 1 (higher resolution still)

Now try runsum(n) = 2, i.e. numbers that are the sum of consecutive integers in exactly two ways:

A spiral for runsum(n) = 2

runsum(n) = 2 (hi-res #1)

runsum(n) = 2 (hi-res #2)

runsum(n) = 2 (hi-res #3)

Why do most of the numbers fall on a diagonal? I don’t know, but I know that the diagonal represents square numbers:

Now try runsum(n) = 3:

A spiral for runsum(n) = 3

runsum(n) = 3 (hi-res)

It’s a densely packed spiral, unlike the spiral for runsum(n) = 4:

A spiral for runsum(n) = 4

runsum(n) = 4 (hi-res)

Like the spiral for runsum(n) = 2, the numbers are disproportionately falling on the diagonal of square numbers:

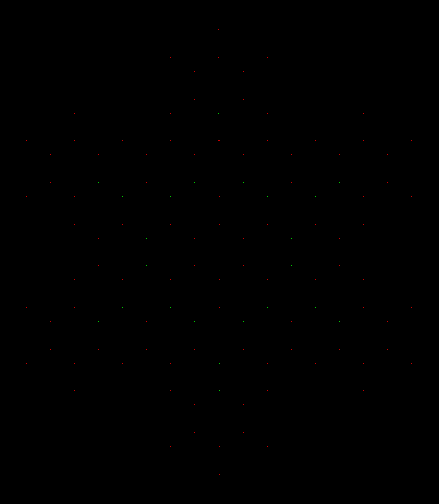
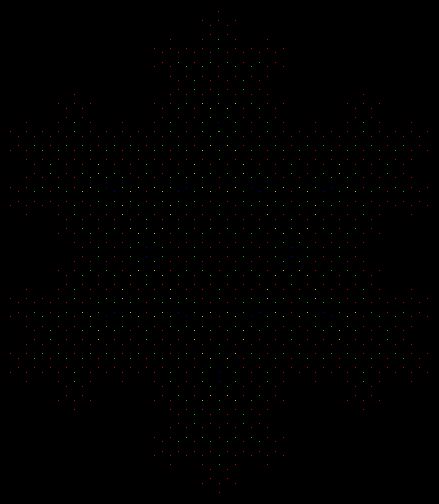
Here are spirals for runsum(n) = 5:

A spiral for runsum(n) = 5 (note patterns in green)

runsum(n) = 5 (hi-res #1)

runsum(n) = 5 (hi-res #2)

There are two interesting patterns in the spiral, marked in green above and enlarged below:

Pattern #1 in spiral for runsum(n) = 5

Pattern #2 in spiral for runsum(n) = 5

Are the patterns merely artefacts or does one or both represent something mathematically significant? I don’t know.

More spirals:

A spiral for runsum(n) = 6

A spiral for runsum(n) = 7

runsum(n) = 7 (hi-res)

A spiral for runsum(n) = 8

runsum(n) = 8 (hi-res #1)

runsum(n) = 8 (hi-res #2)

Numbers in the spiral for runsum(n) = 8 are again falling disproportionately on the diagonal of square numbers. Here’s one of those squares:

Previously Pre-Posted…

• Spiral Artefact #1 — a look at patterns in spirals with different tests