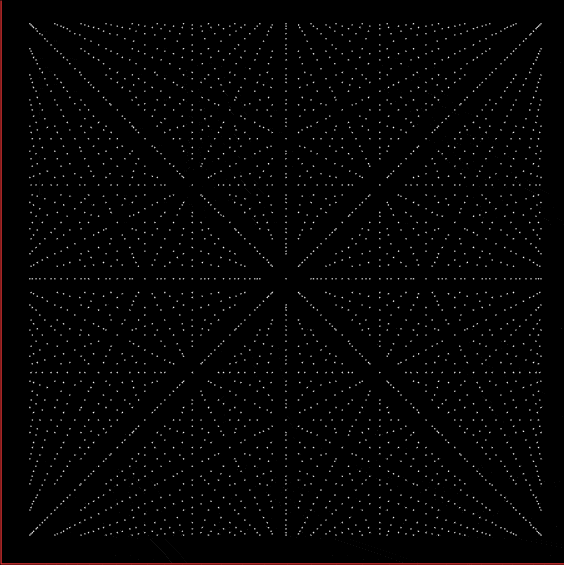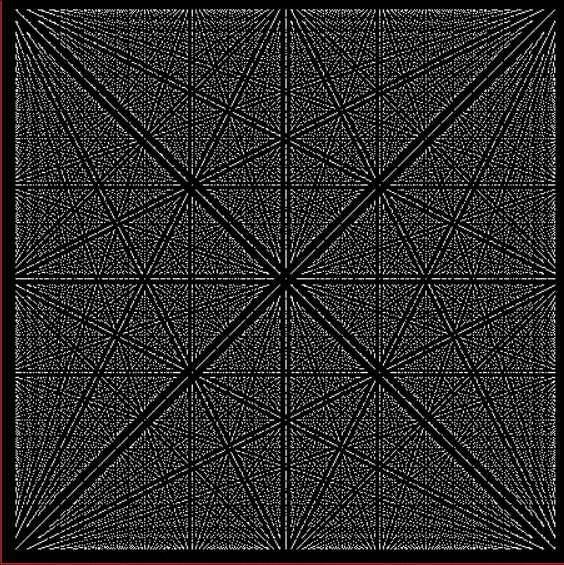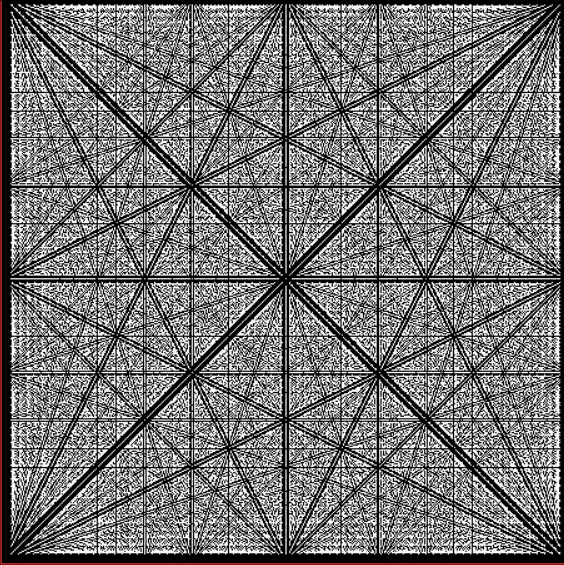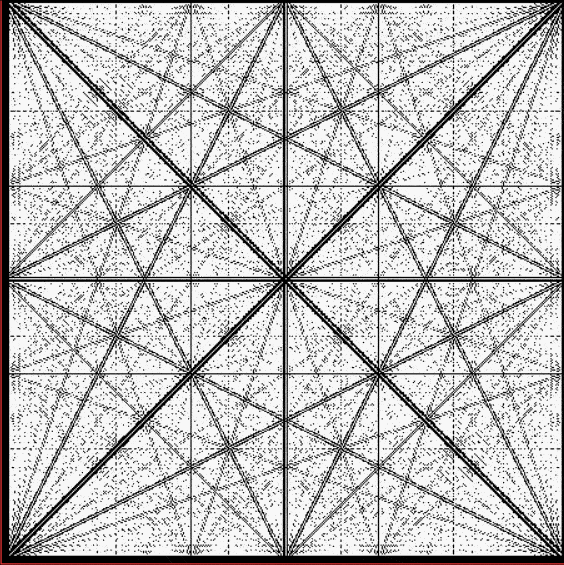
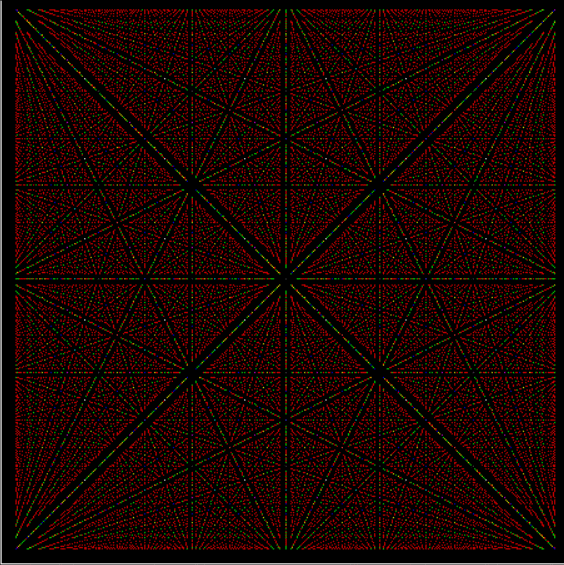
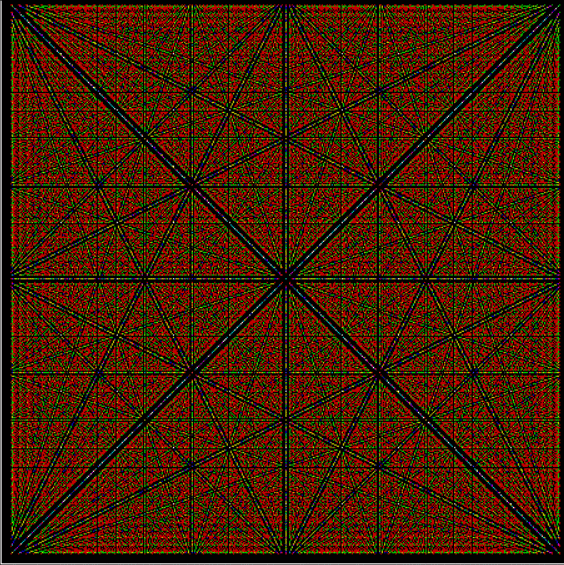
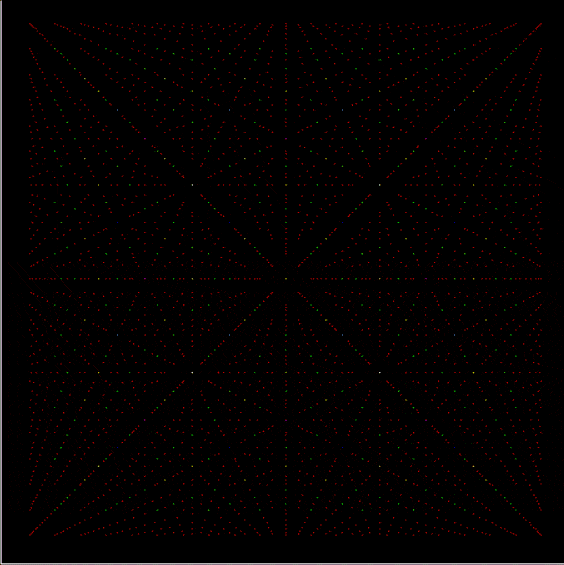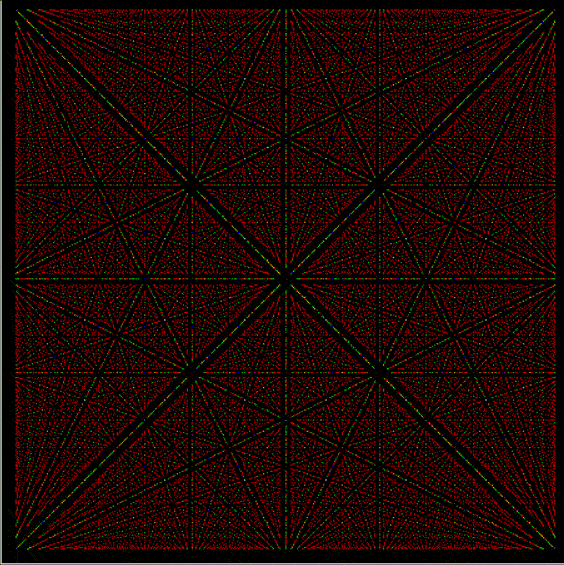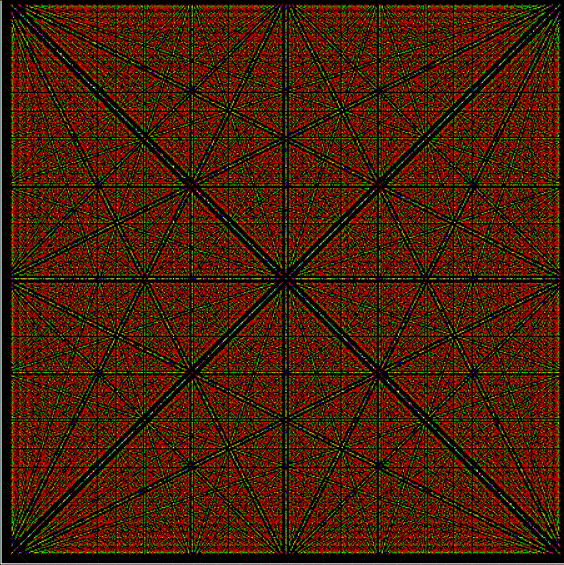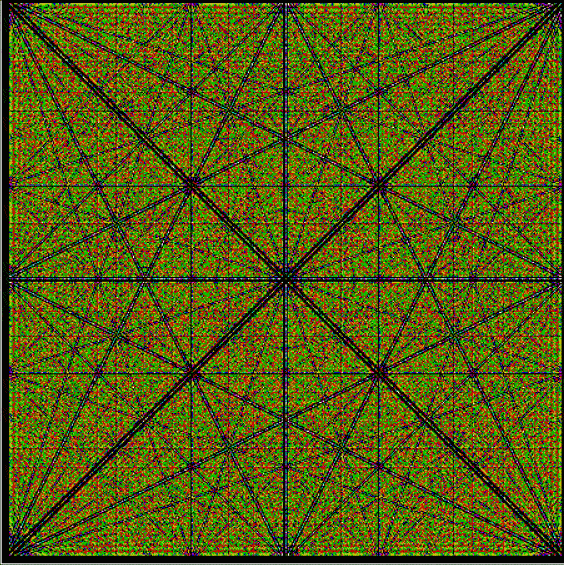
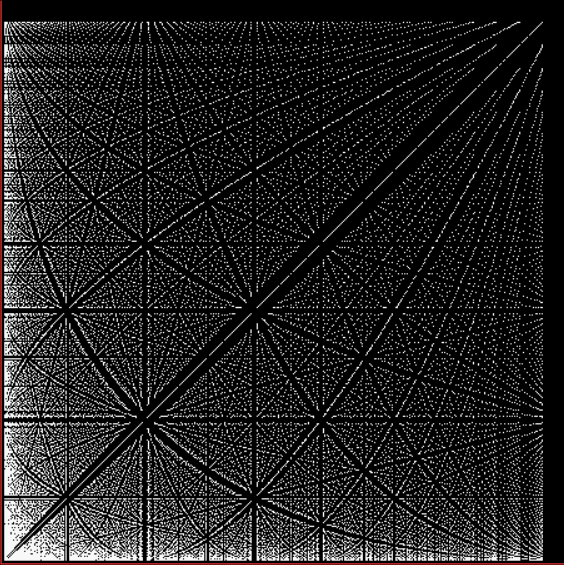
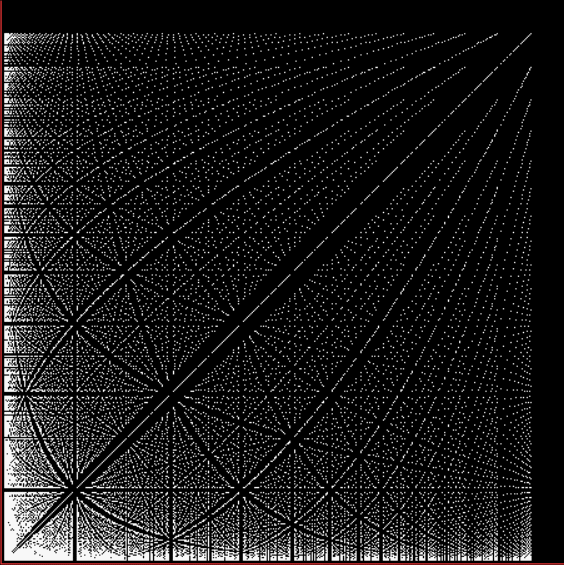
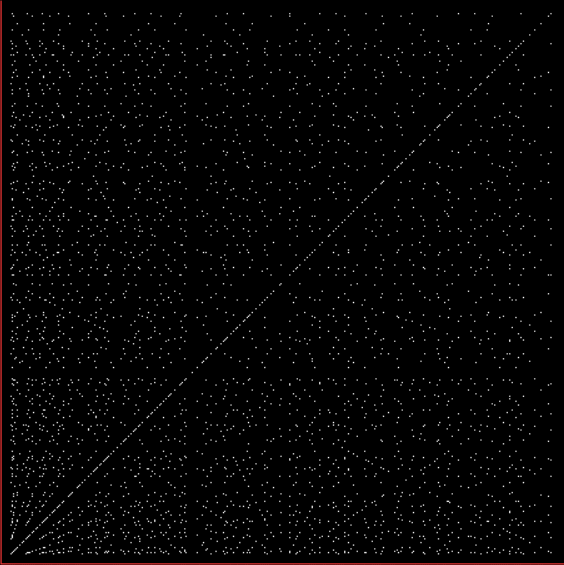
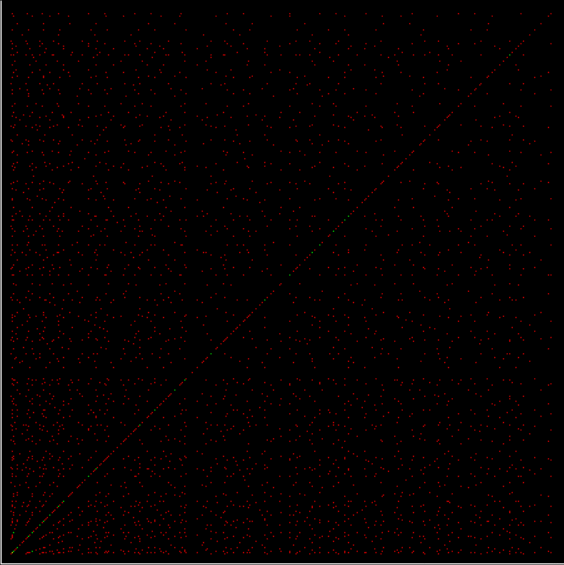
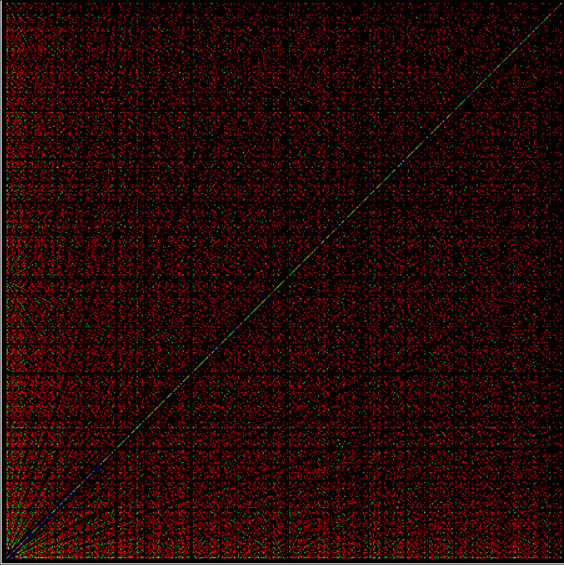
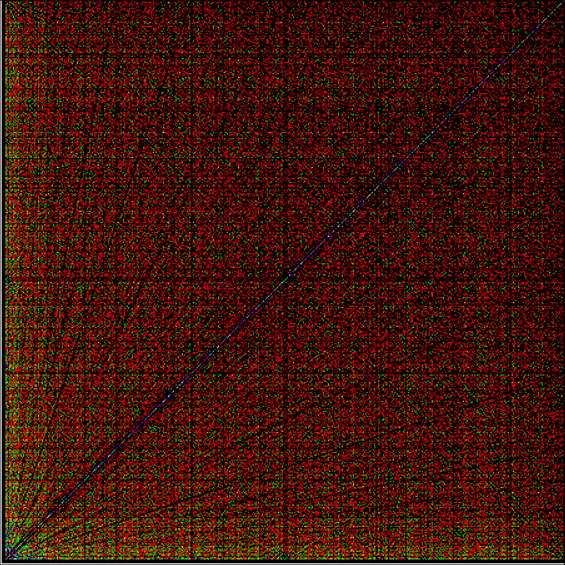
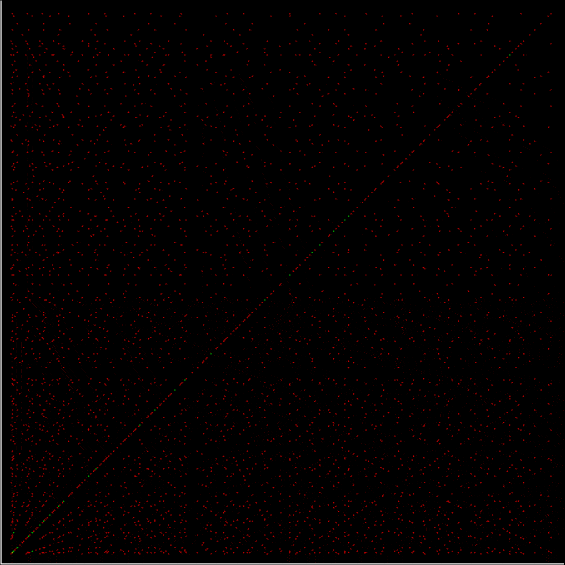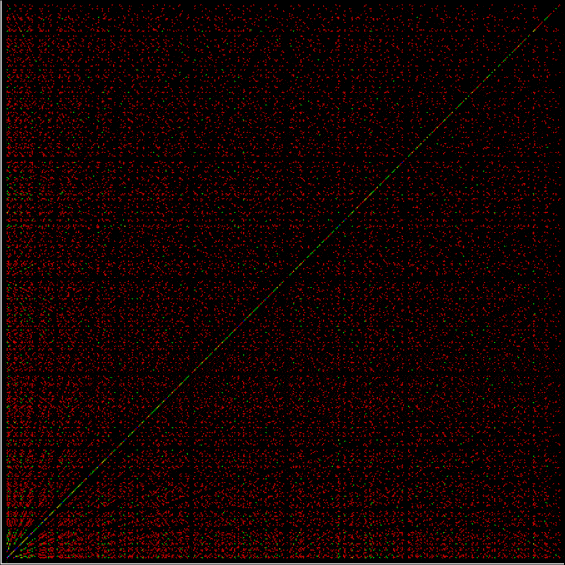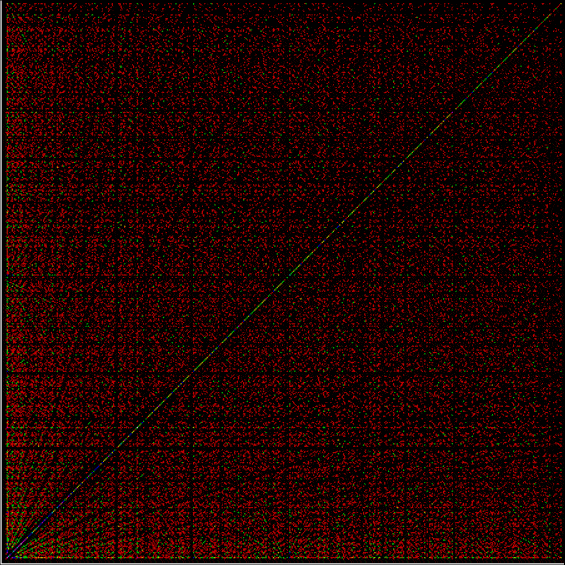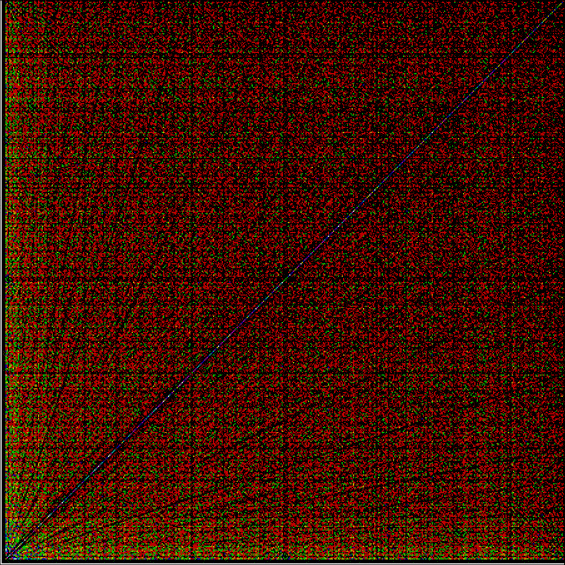
Suppose you set up an L, i.e. a vertical and horizontal line, representing the x,y coordinates between 0 and 1. Next, find the fractional pairs x = 1/2, 1/3, 2/3, 1/4, 2/4…, y = 1/2, 1/3, 2/3, 1/4, 2/4… and mark the point (x,y). That is, find the point, say, 1/5 of the way along the x-line, then the points 1/5, 2/5, 3/5 and 4/5 along the y-line, marking the points (1/5, 1/5), (1/5, 2/5), (1/5, 3/5), (1/5, 4/5). Then find (2/5, 1/5), (2/5, 2/5), (2/5, 3/5), (2/5, 4/5) and so on. Some interesting patterns appear in what I call a Frac-L (pronounced “frackle”) or Fract-L:

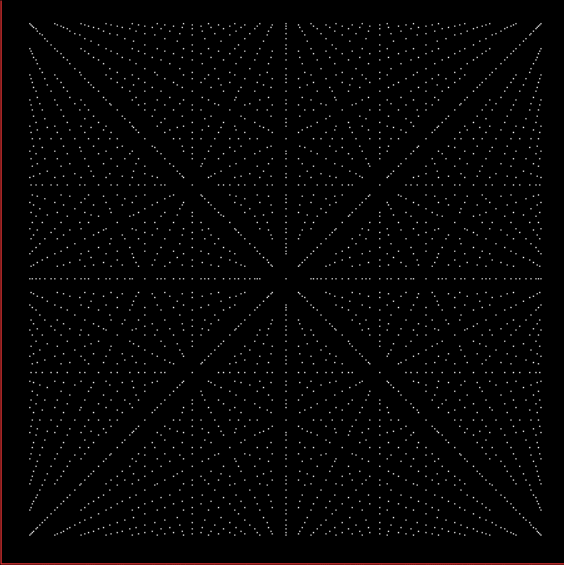
Frac-L for 1/2 to 21/22

---

Frac-L for 1/2 to 48/49

---

Frac-L for 1/2 to 75/76

---

Frac-L for 1/2 to 102/103

---

Frac-L for 1/2 to 102/103 (animated)

---

If the (x,y) point is first red, then becomes different colors as it is repeatedly found, you get these patterns:

Frac-L for 1/2 to 48/49 (color)

---

Frac-L for 1/2 to 75/79 (color)

---

Frac-L for 1/2 to 102/103 (color) (animated)

---

Now try polygonal numbers. The triangular numbers are 1, 3, 6, 10, 15, 21, 28, 36, 45, 55, 66, 78…, so you’re finding the fractional pairs, say, (1/21, 1/21), (1/21, 3/21, (1/21, 6/21), (1/21, 10/21), (1/21, 15/21), then (3/21, 1/21), (3/21, 3/21, (3/21, 6/21), (3/21, 10/21), (3/21, 15/21), and so on:

Frac-L for triangular fractions

---

The frac-L for square numbers (1, 4, 9, 16, 25, 36, 49, 64, 81, 100…) is almost identical:

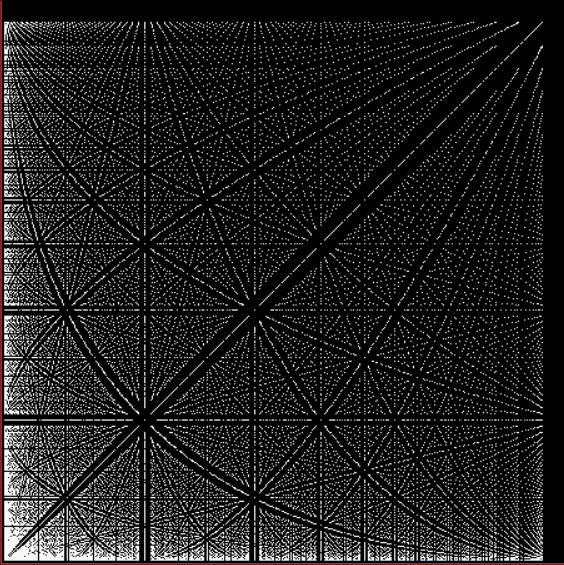
Frac-L for square fractions, e.g. (1/16, 1/16), (1/16, 4/16), (1/16, 9/16)…

---

So is the frac-L for pentagonal numbers (1, 5, 12, 22, 35, 51, 70, 92, 117, 145, 176, 210, 247, 287, 330…):

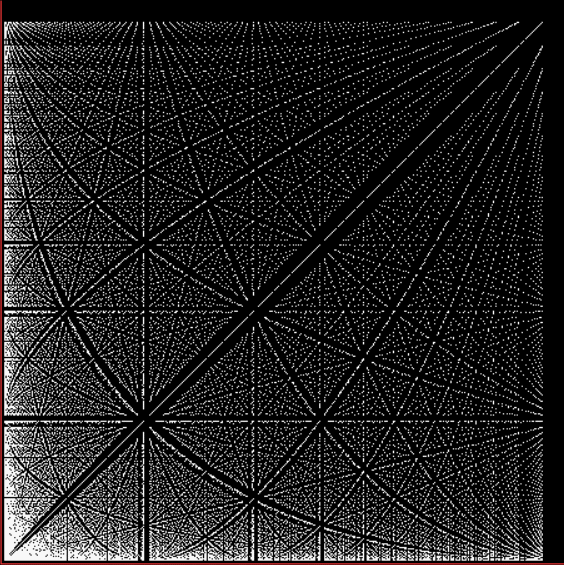
Frac-L for pentagonal fractions, e.g. (1/35, 5/35), (1/35, 12/35), (1/35,22/35)…

---

Here are frac-Ls for tetrahedral and square-pyramidal numbers:

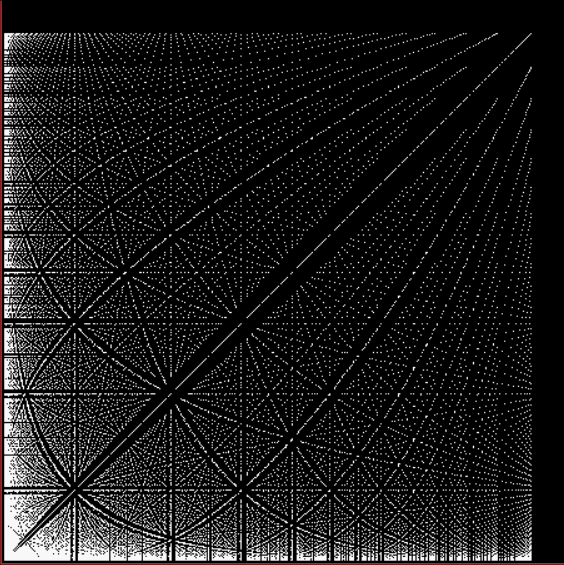
Frac-L for tetrahedral fractions

---

Frac-L for square pyramidal fractions

---

But what about prime numbers (skipping 2)? Here the fractional pairs are, say, (1/17, 1/17), (1/17, 3/17), (1/17, 5/17), (1/17, 7/17), (1/17, 11/17), (1/17, 13/17), then (3/17, 1/17), (3/17, 3/17), (3/17, 5/17), (3/17, 7/17), (3/17, 11/17), (3/17, 13/17), and so on:

Frac-L for 1/3 to 73/79 (prime fractions)

---

Frac-L for 1/3 to 223/227

---

Frac-L for 1/3 to 307/331

---

Frac-L for 1/3 to 307/331 (animated)

---

Frac-L for 1/3 to 73/79 (color) (prime fractions)

---

Frac-L for 1/3 to 223/227 (color)

---

Frac-L for 1/3 to 307/331 (color)

---

Frac-L for 1/3 to 307/331 (color) (animated)

---

And finally (for now), a frac-L for Fibonnaci numbers, where the fractional pairs are, say, (1/13, /13), (1/13, 2/13), (1/13, 3/13), (1/13, 5/13), (1/13, 8/13), then (2/13, /13), (2/13, 2/13), (2/13, 3/13), (2/13, 5/13), (2/13, 8/13), and so on:

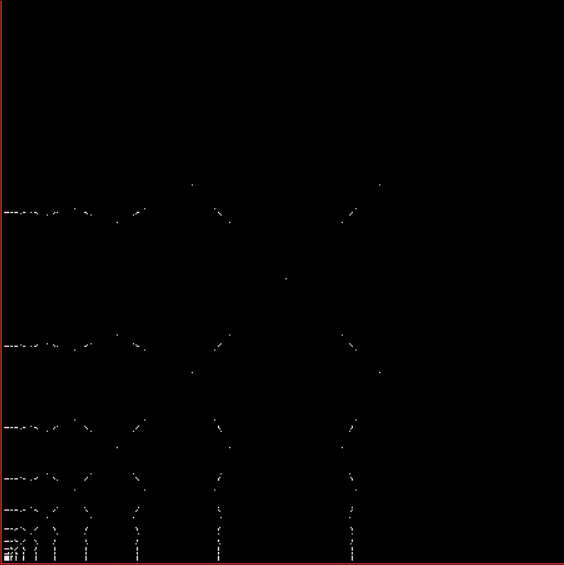
Frac-L for Fibonacci fractions to 14930352/2178309 = fibonacci(36)/fibonacci(37)

---