This simple equation helps you understand a fractal:

1 + 1/2 + 1/4 + 1/8 + 1/16 + 1/32 + … = 2 = Σ(1/2^k,k=0..∞)

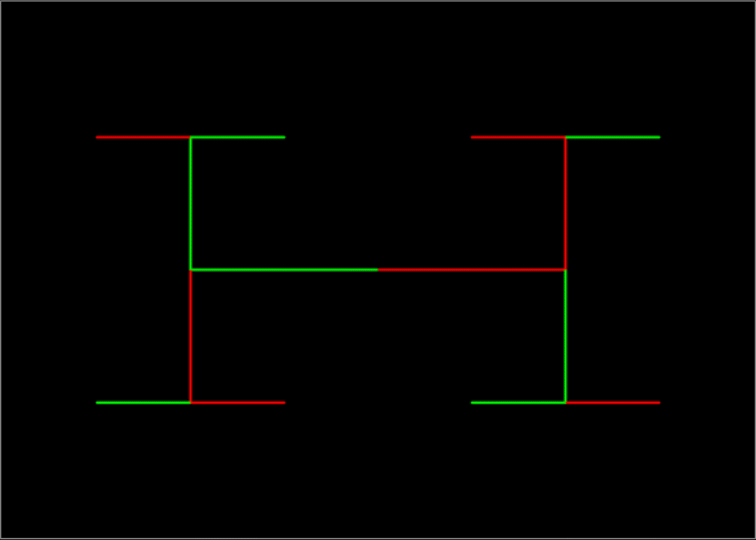
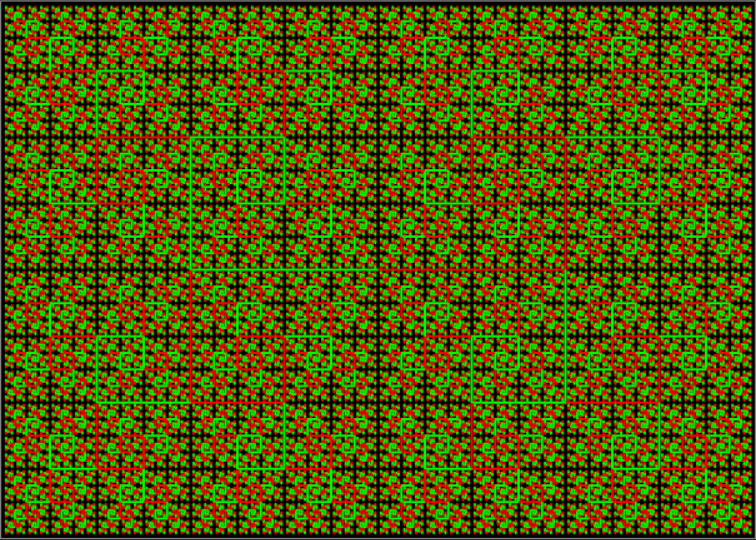
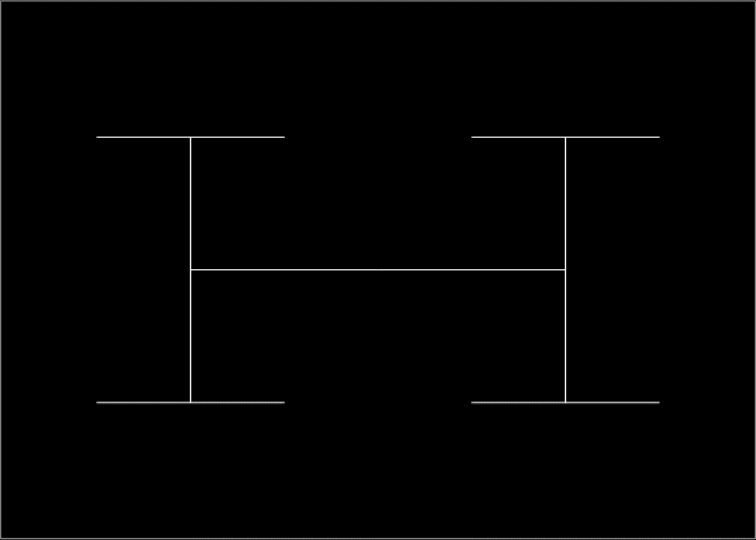
Now here’s the construction of the H-tree fractal, in which the lines are divided in length by sqrt(2) = 1.41421356237… at each stage. Or multiplied by 0.70710678118… = &sqrt;0.5. This means that, after two divisions, the lines are 1/2 the size. So in the end they create a 1 x &sqrt;2 rectangle:

H-Tree fractal #1

---

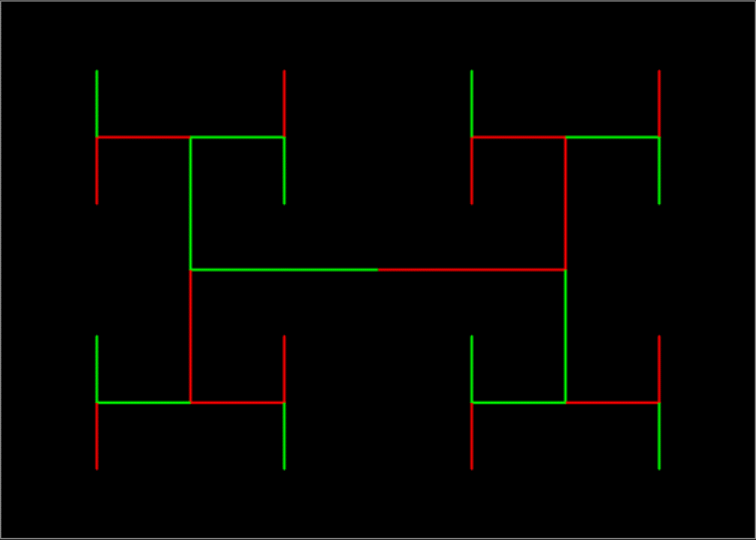
H-Tree fractal #2

---

H-Tree fractal #3

---

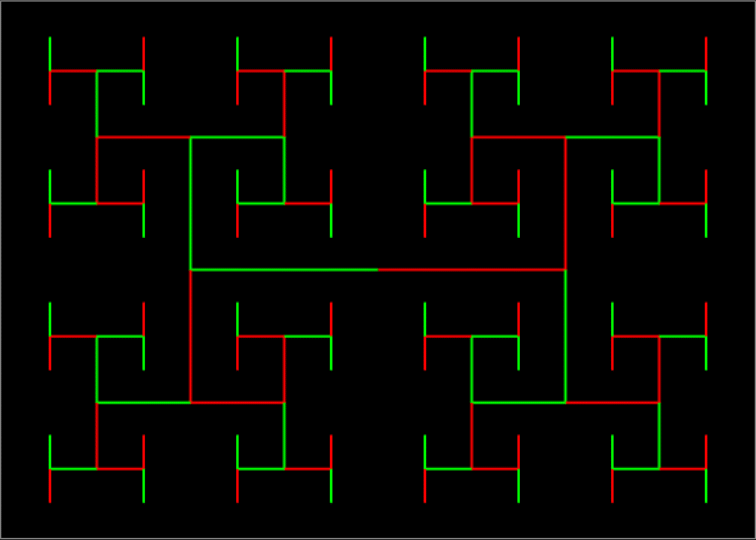
H-Tree fractal #4

---

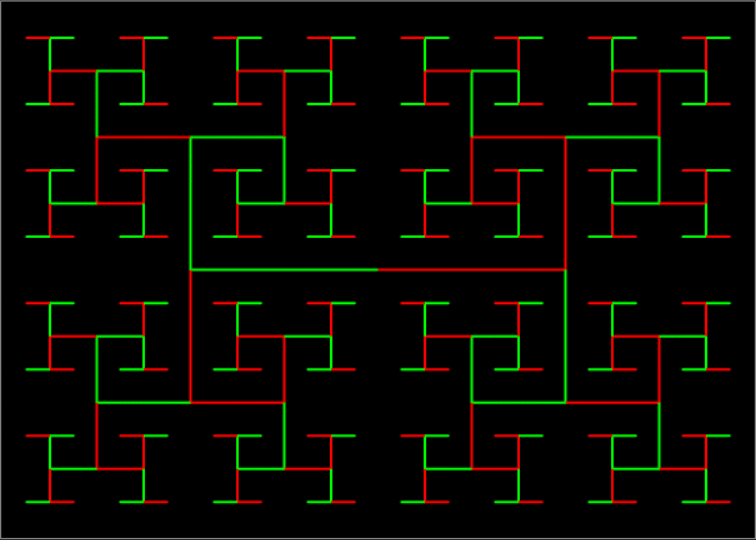
H-Tree fractal #5

---

H-Tree fractal #6

---

H-Tree fractal #7

---

H-Tree fractal #8

---

H-Tree fractal #9

---

H-Tree fractal #10

↓
[…]
↓

H-Tree fractal #13

---

H-Tree fractal #14

---

H-Tree fractal #15

---

Here’s an animation:

H-Tree fractal (animated at EZgif)

---

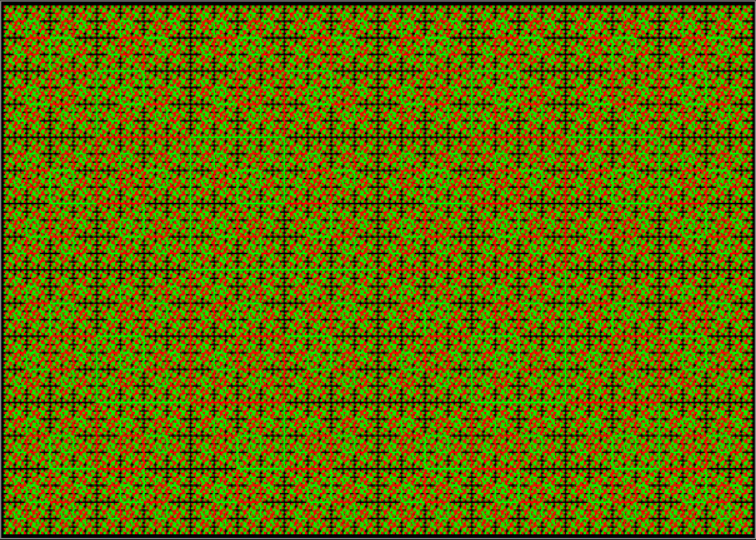
And here’s the H-tree in black-and-white:

H-Tree fractal #3

↓

H-Tree fractal #6

↓

H-Tree fractal #6

↓

H-Tree fractal #12

↓

H-Tree fractal #15

↓

H-Tree fractal (animated at EZgif)

---

Because the construction of the H-tree is governed by a string of directions — for example, left-right-right-left-left-left… or 211222… — you can perform tests on that string to create sub-fractals from the super-fractal. Like this:

count(1) = count(2) in string to step 12

---

count(1) = count(2) in string (omitting lines)

---

sum(string) = mul(string)

---

sum(string) > mul(string)

---

count(1) = 2 or count(2) = 2 after step 2

---

count(1) < count(2)

---

count(1) < 3 or count(2) < 3 after step 6

---

value of string after step 8 > value of string at step 1

---

value after step 8 > value at step 4

---

value after step 8 < value step 1

---

ispalindrome(string) to step 11

---

ispalindrome(string) to step 18

---

ispalindrome(string) to step 20

---

alternating 121… or 212… in string after step 9

---

ispolygonal(sum(string[i]-1),pol=10)

---

isprime(sum(string))

---

sum(string[i]-1) mod 13 = 0

---

sum(string[i]-1) mod 13 = 1

---

sum(string[i]-1) mod 16 = 0

---

sum(string[i]-1) mod 18 = 0

---