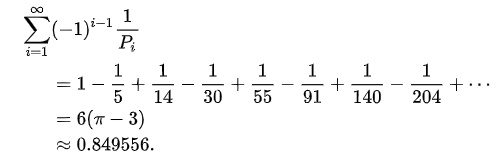These are the odd numbers:

1, 3, 5, 7, 9, 11, 13, 15, 17, 19, 21, 23, 25, 27, 29, 31, 33, 35, 37, 39, 41, 43, 45, 47, 49, 51, 53, 55, 57, 59...

If you add the odd numbers, 1+3+5+7…, you get the square numbers:

1, 4, 9, 16, 25, 36, 49, 64, 81, 100, 121, 144, 169, 196, 225, 256, 289, 324, 361, 400, 441, 484, 529, 576, 625, 676, 729, 784, 841, 900...

And if you add the square numbers, 1+4+9+16…, you get what are called the square pyramidal numbers:

1, 5, 14, 30, 55, 91, 140, 204, 285, 385, 506, 650, 819, 1015, 1240, 1496, 1785, 2109, 2470, 2870, 3311, 3795, 4324, 4900, 5525, 6201, 6930, 7714, 8555, 9455...

There’s not a circle in sight, so you wouldn’t expect to find π amid the pyramids. But it’s there all the same. You can get π from this formula using the square pyramidal numbers:

π from a formula using square pyramidal numbers (Wikipedia)

Here are the approximations getting nearer and near to π:

3.1415926535897932384... = π
3.1666666666666666666... = sqpyra2pi(i=1) / 6 + 3
1 = sqpyra(1)

3.1415926535897932384... = π
3.1452380952380952380... = sqpyra2pi(i=3) / 6 + 3
14 = sqpyra(3)

3.1415926535897932384... = π
3.1412548236077647842... = sqpyra2pi(i=8) / 6 + 3
204 = sqpyra(8)

3.1415926535897932384... = π
3.1415189855952756236... = sqpyra2pi(i=14) / 6 + 3
1,015 = sqpyra(14)

3.1415926535897932384... = π
3.1415990074057163751... = sqpyra2pi(i=33) / 6 + 3
12,529 = sqpyra(33)

3.1415926535897932384... = π
3.1415920110950124679... = sqpyra2pi(i=72) / 6 + 3
127,020 = sqpyra(72)

3.1415926535897932384... = π
3.1415926017980070553... = sqpyra2pi(i=168) / 6 + 3
1,594,684 = sqpyra(168)

3.1415926535897932384... = π
3.1415926599504002195... = sqpyra2pi(i=339) / 6 + 3
13,043,590 = sqpyra(339)

3.1415926535897932384... = π
3.1415926530042565359... = sqpyra2pi(i=752) / 6 + 3
142,035,880 = sqpyra(752)

3.1415926535897932384... = π
3.1415926535000384883... = sqpyra2pi(i=1406) / 6 + 3
927,465,791 = sqpyra(1406)

3.1415926535897932384... = π
3.1415926535800054618... = sqpyra2pi(i=2944) / 6 + 3
8,509,683,520 = sqpyra(2944)

3.1415926535897932384... = π
3.1415926535890006043... = sqpyra2pi(i=6806) / 6 + 3
105,111,513,491 = sqpyra(6806)

3.1415926535897932384... = π
3.1415926535897000092... = sqpyra2pi(i=13892) / 6 + 3
893,758,038,910 = sqpyra(13892)

3.1415926535897932384... = π
3.1415926535897999990... = sqpyra2pi(i=33315) / 6 + 3
12,325,874,793,790 = sqpyra(33315)

3.1415926535897932384... = π
3.1415926535897939999... = sqpyra2pi(i=68985) / 6 + 3
109,433,980,000,485 = sqpyra(68985)

3.1415926535897932384... = π
3.1415926535897932999... = sqpyra2pi(i=159563) / 6 + 3
1,354,189,390,757,594 = sqpyra(159563)

3.1415926535897932384... = π
3.1415926535897932300... = sqpyra2pi(i=309132) / 6 + 3
9,847,199,658,130,890 = sqpyra(309132)

3.1415926535897932384... = π
3.1415926535897932389... = sqpyra2pi(i=774865) / 6 + 3
155,080,688,289,901,465 = sqpyra(774865)

3.1415926535897932384... = π
3.1415926535897932384... = sqpyra2pi(i=1586190) / 6 + 3
1,330,285,259,163,175,415 = sqpyra(1586190)