It’s an interesting little exercise in elementary trigonometry to turn the Sierpiński triangle…

A Sierpiński triangle

---

…into its circular equivalent:

A Sierpiński trisc

---

You could call that a trisc, because it’s a triangle turned into a disc. And here’s triangle-and-trisc in one image:

Sierpiński triangle + Sierpiński trisc

---

But what’s the square equivalent of a Sierpiński triangle? This is:

Square from Sierpiński triangle

---

You can do that directly, as it were:

Sierpiński triangle → square

---

Or you can convert the triangle into a disc, then the disc into a square, like this:

Sierpiński triangle → trisc → square

---

Now try converting the triangle into a pentagon:

Pentagon from Sierpiński triangle

---

Sierpiński triangle → pentagon

---

Sierpiński triangle → trisc → pentagon

---

And a hexagon:

Hexagon from Sierpiński triangle

---

Sierpiński triangle → hexagon

---

Sierpiński triangle → trisc → hexagon

---

But you can also convert the Sierpiński trisc back into a Sierpiński triangle, then into a Sierpiński trisc again:

Sierpiński triangle → trisc → triangle → trisc

---

Sierpiński triangle → trisc → triangle → trisc (animated at Ezgif)

---

Sierpiński triangle → trisc → triangle → trisc (b&w)

---

Sierpiński triangle → trisc → triangle → trisc (b&w) (animated at Ezgif)

---

After triangles come squares. Here’s a shape called a T-square fractal:

T-square fractal

---

And here’s the circular equivalent of a T-square fractal:

T-square fractal → T-squisc

---

T-square fractal + T-squisc

---

If a disc from a triangle is a trisc, then a disc from a square is a squisc (it would be pentisc, hexisc, heptisc for pentagonal, hexagonal and heptagonal fractals). Here’s the octagonal equivalent of a T-square fractal:

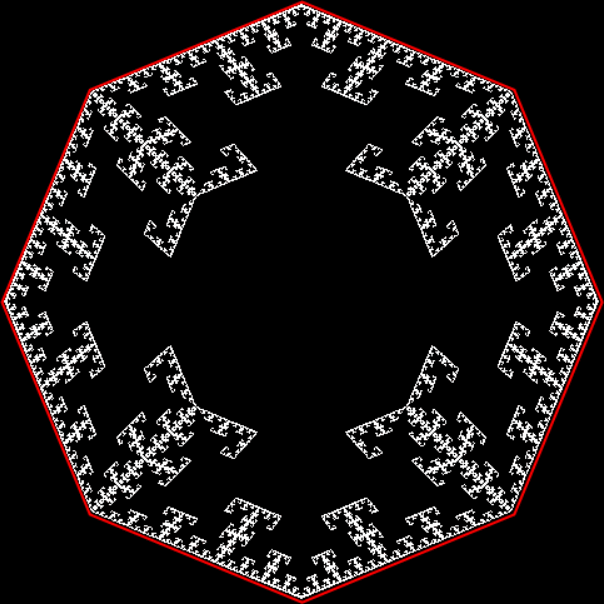
Octagon from T-square fractal

---

As with the Sierpiński trisc, you can use the T-squisc to create the T-octagon:

T-square fractal → T-squisc → T-octagon (color)

---

Or you can convert the T-square directly into the T-octagon:

T-square fractal to T-octagon fractal

But using the squisc makes for interesting multiple images:

---

T-square fractal → T-squisc → T-octagon (b&w)

---

T-square fractal → T-squisc → T-octagon → T-squisc

---

T-square fractal → T-squisc → T-octagon → T-squisc (animated at Ezgif)

---

The conversions from polygon to polygon look best when the number of sides in the higher polygon are a multiple of the number of sides in the lower, like this:

Sierpiński triangle → Sierpiński hexagon → Sierpiński nonagon

---