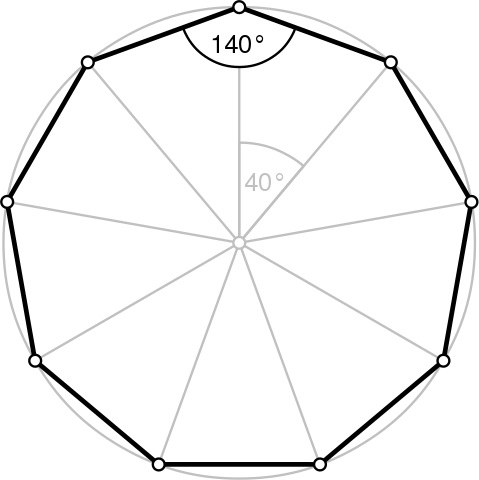
This is a regular nonagon (a polygon with nine sides):

A nonagon or enneagon (from Wikipedia)

And this is the endlessly repeating decimal of the reciprocal of 7:

1/7 = 0.142857142857142857142857…

What is the curious connection between 1/7 and nonagons? If I’d been asked that a week ago, I’d’ve had no answer. Then I found a curious connection when I was looking at the leading digits of polygonal numbers. A polygonal number is a number that can be represented in the form of a polygon. Triangular numbers look like this:

* = 1

*
** = 3

*
**
*** = 6

*
**
***
**** = 10

*
**
***
****
***** = 15

By looking at the shapes rather than the numbers, it’s easy to see that you generate the triangular numbers by simply summing the integers:

1 = 1
1+2=3
1+2+3=6
1+2+3+4=10
1+2+3+4+5=15

Now try the square numbers:

* = 1

**
** = 4

***
***
*** = 9

****
****
****
**** = 16

*****
*****
*****
*****
***** = 25

You generate the square numbers by summing the odd integers:

1 = 1
1+3 = 4
1+3+5 = 9
1+3+7 = 16
1+3+7+9 = 25

Next come the pentagonal numbers, the hexagonal numbers, the heptagonal numbers, and so on. I was looking at the leading digits of these numbers and trying to find patterns. For example, when do the leading digits of the k-th triangular number, tri(k), match the digits of k? This is when:

tri(1) = 1
tri(19) = 190
tri(199) = 19900
tri(1999) = 1999000
tri(19999) = 199990000
tri(199999) = 19999900000
[...]

That pattern is easy to explain. The formula for the k-th polygonal number is k * ((pn-2)*k + (4-pn)) / 2, where pn = 3 for the triangular numbers, 4 for the square numbers, 5 for the pentagonal numbers, and so on. Therefore the k-th triangular number is k * (k + 1) / 2. When k = 19, the formula is 19 * (19 + 1) / 2 = 19 * 20 / 2 = 19 * 10 = 190. And so on. Now try the pol(k) = leaddig(pol(k)) for higher polygonal numbers. The patterns are easy to predict until you get to the nonagonal numbers:

square(10) = 100
square(100) = 10000
square(1000) = 1000000
square(10000) = 100000000
square(100000) = 10000000000
[...]

---

pentagonal(7) = 70
pentagonal(67) = 6700
pentagonal(667) = 667000
pentagonal(6667) = 66670000
pentagonal(66667) = 6666700000
[...]

---

hexagonal(6) = 66
hexagonal(51) = 5151
hexagonal(501) = 501501
hexagonal(5001) = 50015001
hexagonal(50001) = 5000150001
[...]

---

heptagonal(5) = 55
heptagonal(41) = 4141
heptagonal(401) = 401401
heptagonal(4001) = 40014001
heptagonal(40001) = 4000140001
[...]

---

octagonal(4) = 40
octagonal(34) = 3400
octagonal(334) = 334000
octagonal(3334) = 33340000
octagonal(33334) = 3333400000
[...]

---

nonagonal(4) = 46
nonagonal(30) = 3075
nonagonal(287) = 287574
nonagonal(2858) = 28581429
nonagonal(28573) = 2857385719
nonagonal(285715) = 285715000000
nonagonal(2857144) = 28571444285716
nonagonal(28571430) = 2857143071428575
nonagonal(285714287) = 285714287571428574
nonagonal(2857142858) = 28571428581428571429
nonagonal(28571428573) = 2857142857385714285719
nonagonal(285714285715) = 285714285715000000000000
nonagonal(2857142857144) = 28571428571444285714285716
nonagonal(28571428571430) = 2857142857143071428571428575
nonagonal(285714285714287) = 285714285714287571428571428574
nonagonal(2857142857142858) = 28571428571428581428571428571429
nonagonal(28571428571428573) = 2857142857142857385714285714285719
nonagonal(285714285714285715) = 285714285714285715000000000000000000
nonagonal(2857142857142857144) = 28571428571428571444285714285714285716
nonagonal(28571428571428571430) = 2857142857142857143071428571428571428575
[...]

What’s going on with the leading digits of the nonagonals? Well, they’re generating a different reciprocal. Or rather, they’re generating the multiple of a different reciprocal:

1/7 * 2 = 2/7 = 0.285714285714285714285714285714...

And why does 1/7 have this curious connection with the nonagonal numbers? Because the nonagonal formula is k * (7k-5) / 2 = k * ((9-2) * k + (4-pn)) / 2. Now look at the pentadecagonal numbers, where pn = 15:

pentadecagonal(1538461538461538461540) = 15384615384615384615406923076923076923076930

2/13 = 0.153846153846153846153846153846...

pentadecagonal formula = k * (13k - 11) / 2 = k * ((15-2)*k + (4-15)) / 2

Penultimately, let’s look at the icosikaihenagonal numbers, where pn = 21:

icosikaihenagonal(2) = 21
icosikaihenagonal(12) = 1266
icosikaihenagonal(107) = 107856
icosikaihenagonal(1054) = 10544743
icosikaihenagonal(10528) = 1052878960
icosikaihenagonal(105265) = 105265947385
icosikaihenagonal(1052633) = 10526335263165
icosikaihenagonal(10526317) = 1052631731578951
icosikaihenagonal(105263159) = 105263159210526318
icosikaihenagonal(1052631580) = 10526315801578947370
icosikaihenagonal(10526315791) = 1052631579163157894746
icosikaihenagonal(105263157896) = 105263157896368421052636
icosikaihenagonal(1052631578949) = 10526315789497368421052643
icosikaihenagonal(10526315789475) = 1052631578947542105263157900
icosikaihenagonal(105263157894738) = 105263157894738263157894736845
icosikaihenagonal(1052631578947370) = 10526315789473706842105263157905
icosikaihenagonal(10526315789473686) = 1052631578947368689473684210526331
icosikaihenagonal(105263157894736843) = 105263157894736843000000000000000000
icosikaihenagonal(1052631578947368422) = 10526315789473684220526315789473684211
icosikaihenagonal(10526315789473684212) = 1052631578947368421257894736842105263166

2/19 = 0.1052631578947368421052631579

icosikaihenagonal formula = k * (19k - 17) / 2 = k * ((21-2)*k + (4-21)) / 2

And ultimately, let’s look at this other pattern in the leading digits of the triangular numbers, which I can’t yet explain at all:

tri(904) = 409060
tri(6191) = 19167336
tri(98984) = 4898965620
tri(996694) = 496699963165
tri(9989894) = 49898996060565
tri(99966994) = 4996699994681515
tri(999898994) = 499898999601055515
tri(9999669994) = 49996699999451815015
tri(99998989994) = 4999898999960055555015
tri(999996699994) = 499996699999945018150015
tri(9999989899994) = 49999898999996005055550015
tri(99999966999994) = 4999996699999994500181500015
tri(999999898999994) = 499999898999999600500555500015
[...]