Seq’ and ye shall find. So what’s the next number in this sequence?
1, 1, 3, 1, 5, 3, 7, 1, 9, 5, 11, 3, 13, 7, 15, 1, 17, 9, 19, ?
It’s simple once you’ve spotted the rule. List the counting numbers. If a number is a multiple of 2, divide it by 2 until it’s no longer a multiple of 2 and it becomes what I call a 2-residue. Like this:
reduce(2,n) = 1, 2 → 1, 3, 4 → 2 → 1, 5, 6 → 3, 7, 8 → 4 → 2 → 1, 9, 10 → 5, 11, 12 → 6 → 3, 13, 14 → 7, 15, 16 → 8 → 4 → 2 → 1, 17, 18 → 9, 19, 20 → 10 → 5... — A000265 at the Online Encyclopedia of Integer Sequences (OEIS)
So the next number was 5. Now, what’s the next number in this sequence?
1, 2, 1, 4, 5, 2, 7, 8, 1, 10, 11, 4, 13, 14, 5, 16, 17, 2, 19, 20, ?
The rule now is: divide multiples of 3 by 3 until they’re no longer multiples of 3.
reduce(3,n) = 1, 2, 1, 4, 5, 2, 7, 8, 1, 10, 11, 4, 13, 14, 5, 16, 17, 2, 19, 20, 7, 22, 23, 8, 25, 26, 1, 28, 29, 10, 31, 32, 11, 34, 35, 4, 37, 38, 13, 40, 41, 14, 43, 44, 5, 46, 47, 16, 49, 50, 17, 52, 53, 2, 55, 56, 19, 58, 59, 20, 61, 62, 7, 64, 65, 22, 67, 68, 23, 70, 71, 8, 73, 74, 25, 76, ... — A038502 at OEIS
So the next number is 7, the 3-residue of 21. After looking at these sequences, I did what I usually did and tried them on an Ulam spiral. The sum of reduce(2,n) is this:
1, 2, 5, 6, 11, 14, 21, 22, 31, 36, 47, 50, 63, 70, 85, 86, 103, 112, 131, 136, 157, 168, 191, 194, 219, 232, 259, 266, 295, 310, 341, 342, 375, 392, 427, 436, 473, 492, 531, 536, 577, 598, 641, 652, 697, 720, 767, 770, 819, 844, 895, 908, 961, 988, 1043, 1050, 1107, 1136, 1195, 1210, 1271, 1302, 1365, 1366, 1431, 1464, 1531, 1548, 1617, 1652, 1723, 1732, 1805, 1842, 1917, 1936, 2013, 2052, 2131, 2136, 2217, 2258, 2341, 2362, 2447, 2490, 2577, 2588, 2677, 2722, 2813, 2836, 2929, 2976... — A135013 at OEIS
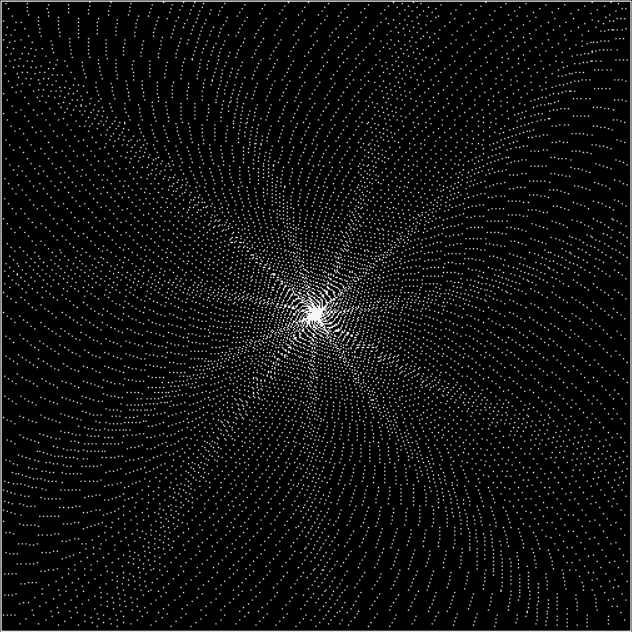
And on an Ulam spiral, the sequence looks like this:
Ulam-like spiral for sum(reduce(2,n)) = 1, 2, 5, 6, 11, 14, 21, 22, 31, 36, 47…
Here are more ResidUlam spirals (not all at the same resolution):
Spiral for sum(reduce(3,n))
Spiral for sum(reduce(4,n))
Spiral for sum(reduce(10,n))
Spiral for sum(reduce(11,n))
Spiral for sum(reduce(18,n))
Spiral for sum(reduce(28,n))
Spiral for sum(reduce(51,n))
N.B. THe 51-ResidUlam doesn’t look like that because the numbers are thinning, but because sum(reduce(51,n)) concentrates them in certain parts of the spiral. Compare sum(reduce(64,n)):
Spiral for sum(reduce(64,n))
Next, you can try reducing numbers with more than one multiple. For example, if you reduce the counting numbers by 2 and 3, you get this sequence:
reduce(2,3,n) = 1, 1, 1, 1, 5, 1, 7, 1, 1, 5, 11, 1, 13, 7, 5, 1, 17, 1, 19, 5, 7, 11, 23, 1, 25, 13, 1, 7, 29, 5, 31, 1, 11, 17, 35, 1, 37, 19, 13, 5, 41, 7, 43, 11, 5, 23, 47, 1, 49, 25, 17, 13, 53, 1, 55, 7, 19, 29, 59, 5, 61, 31, 7, 1, 65, 11, 67, 17, 23, 35, 71, 1, 73, 37, 25, 19, 77, 13, 79, 5, 1, ... — A065330 at OEIS
sum(reduce(2,3,n)) = 1, 2, 3, 4, 9, 10, 17, 18, 19, 24, 35, 36, 49, 56, 61, 62, 79, 80, 99, 104, 111, 122, 145, 146, 171, 184, 185, 192, 221, 226, 257, ...
On an ResiduUlam spiral, sum(reduce(2,3,n)) looks like this at higher and higher resolution:
Spiral for sum(reduce(2,3,n)) #1
Spiral for sum(reduce(2,3,n)) #2
Spiral for sum(reduce(2,3,n)) #3
Spiral for sum(reduce(2,3,n)) #4
Now try another double-reducer:
reduce(6,3,n) = 1, 2, 1, 4, 5, 1, 7, 8, 1, 10, 11, 2, 13, 14, 5, 16, 17, 1, 19, 20, 7, 22, 23, 4, 25, 26, 1, 28, 29, 5, 31, 32, 11, 34, 35, 1, 37, 38, 13, 40, 41, 7, 43, 44, 5, 46, 47, 8, 49, 50, 17, 52, 53, 1, 55, 56, 19, 58, 59, 10, 61, 62, 7, 64, 65, 11, 67, 68, 23, ...
sum(reduce(6,3,n)) = 1, 3, 4, 8, 13, 20, 28, 29, 39, 50, 52, 65, 79, ...
Note that it’s important to reduce by 6 before reducing by 3 (reducing by 3 first would mean no numbers to reduce by 6). Here’s the ResidUlam spiral:
Spiral for sum(reduce(6,3,n)) #1
Spiral for sum(reduce(6,3,n)) #2
Spiral for sum(reduce(6,3,n)) #3
Spiral for sum(reduce(6,3,n)) #4
And two more double-multiple ResidUlams:
Spiral for sum(reduce(7,3,n))
Spiral for sum(reduce(10,8,n))
Overlord In Terms of Core Issues Around Maximal Engagement with Key Notions of the Über-Feral 