Here is an equilateral triangle divided into nine smaller equilateral triangles:

Rep-9 equilateral triangle
The triangle is a rep-tile — it’s tiled with repeating copies of itself. In this case, it’s a rep-9 triangle. Each of the nine smaller triangles can obviously be divided in their turn:

Rep-81 equilateral triangle
Rep-729 equilateral triangle
Rep-729 equilateral triangle again
Rep-6561 equilateral triangle
Rep-9 triangle repeatedly subdividing (animated)
How try trimming the original rep-9 triangle, picking one of the trimmings, and repeating in finer detail. If you choose six triangles in this pattern, you can create a symmetrical braided fractal:
Triangular fractal stage 1
Triangular fractal #2
Triangular fractal #3
Triangular fractal #3 (cleaning up)
Triangular fractal #3 (cleaning up more)
Triangular fractal #4
Triangular fractal #5
Triangular fractal #6
Triangular fractal (animated)
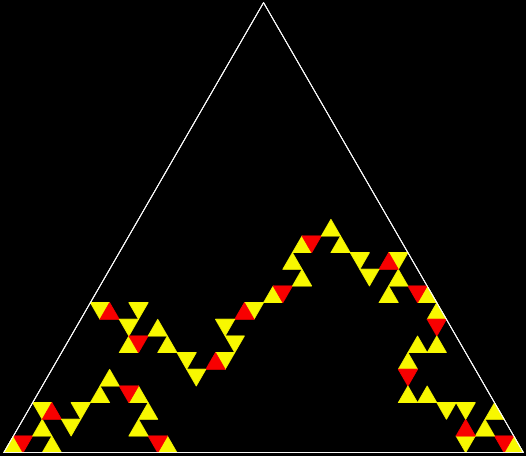
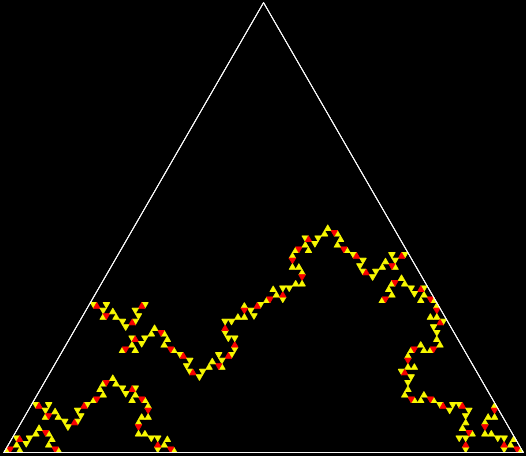
But this fractal using a three-triangle trim-picking isn’t symmetrical:
Trim-picking #1
Trim-picking #2
Trim-picking #3
Trim-picking #4
Trim-picking #5
To make it symmetric, you have to delay the trim, using the full rep-9 trim for the first stage:
Delayed trim-picking #1
Delayed trim-picking #2
Delayed trim-picking #3
Delayed trim-picking #4
Delayed trim-picking #5
Delayed trim-picking #6 (with first two stages as rep-9)
Delayed trim-picking (animated)
Here are some more delayed trim-pickings used to created symmetrical patterns: