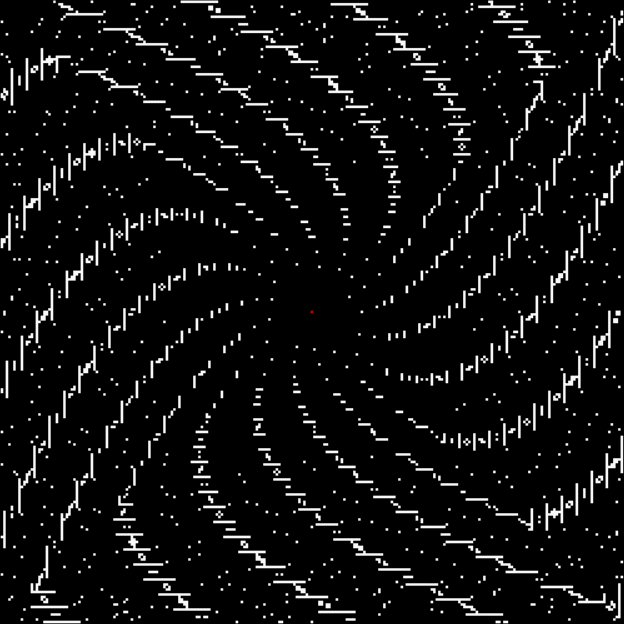
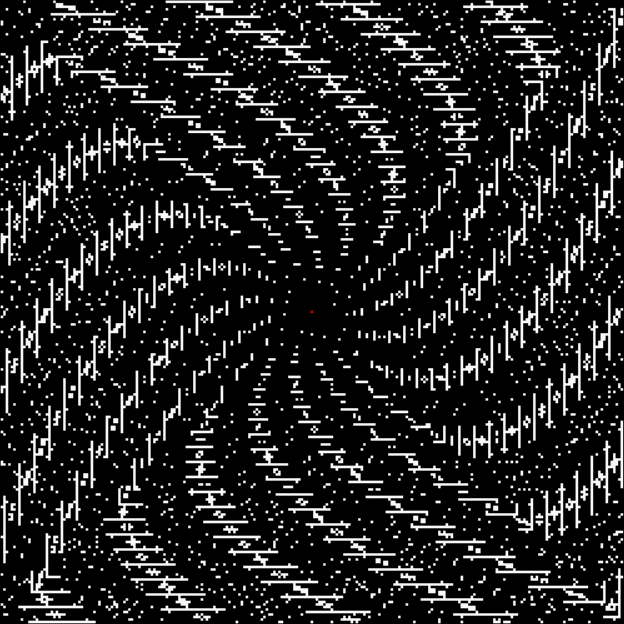
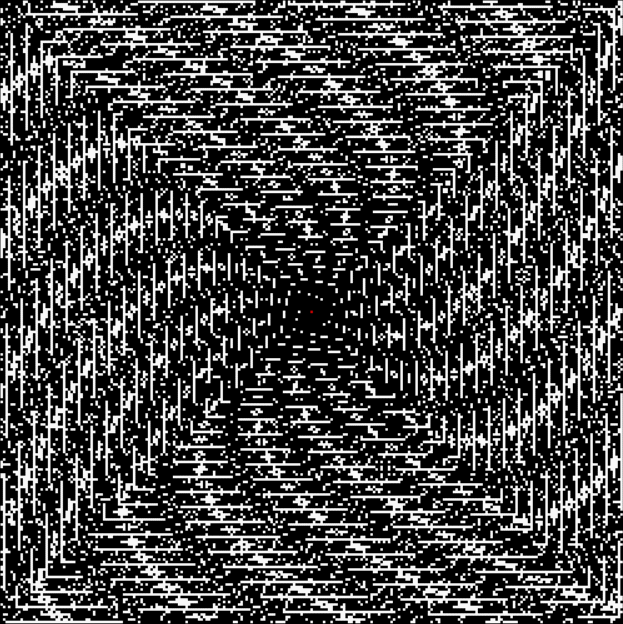
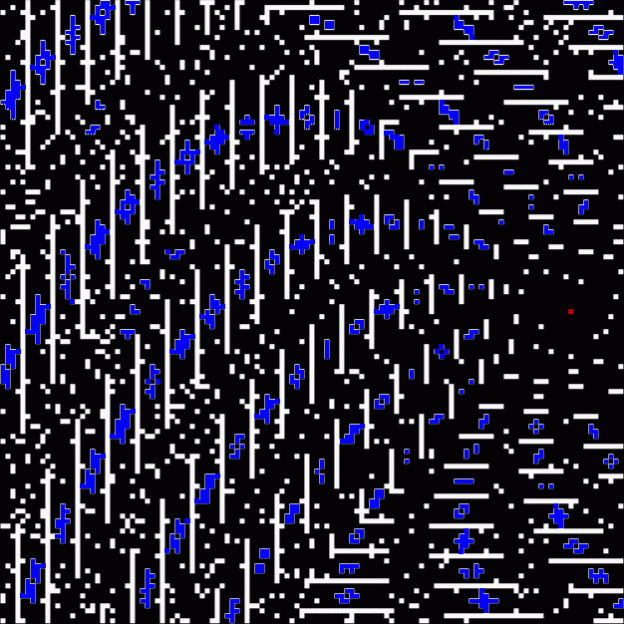
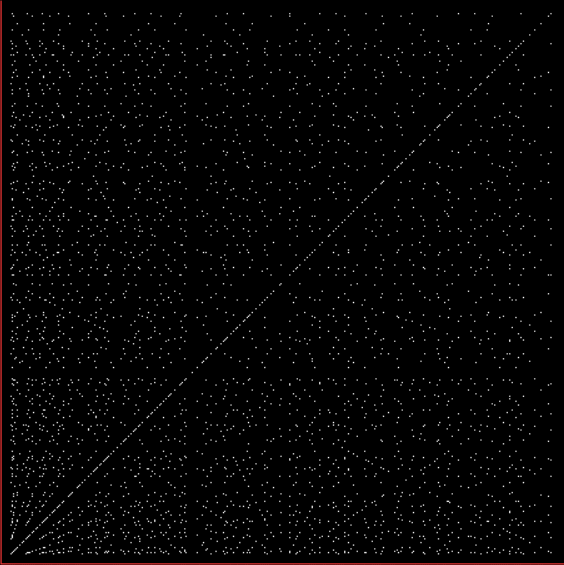
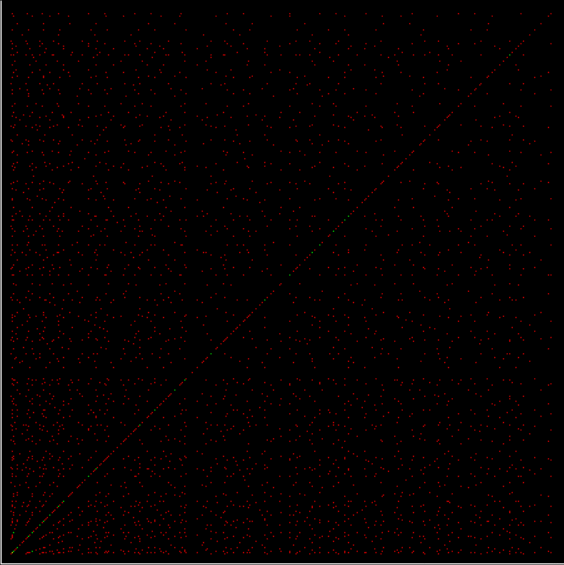
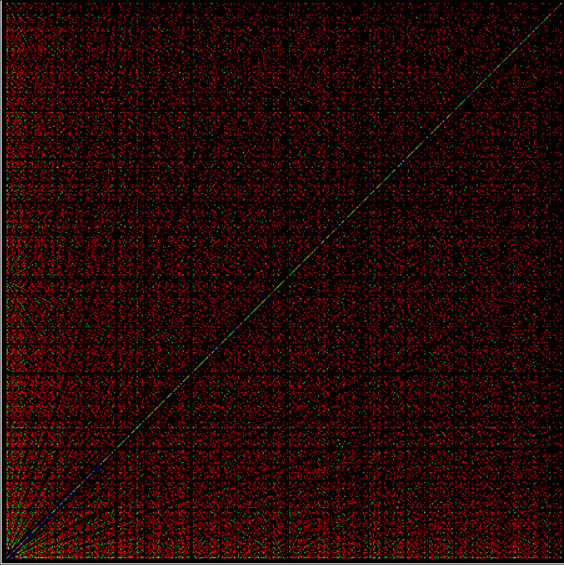
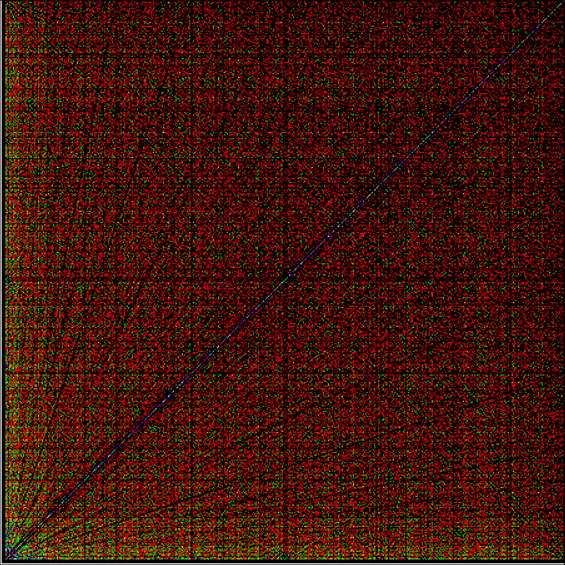
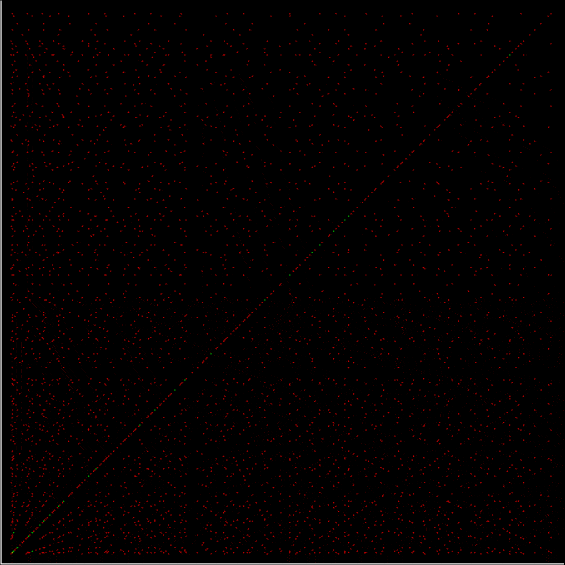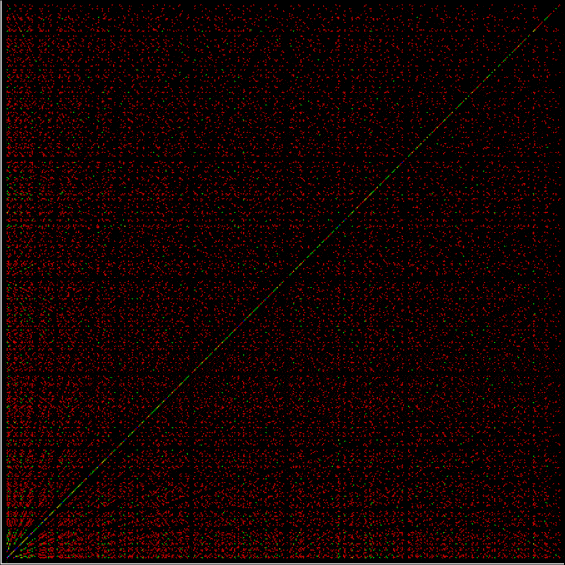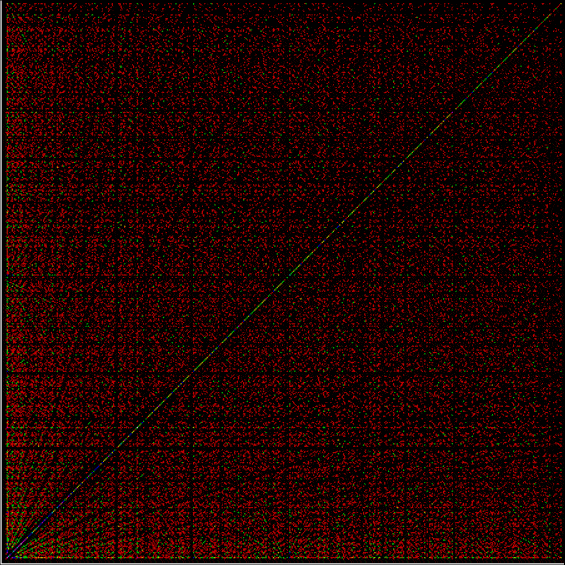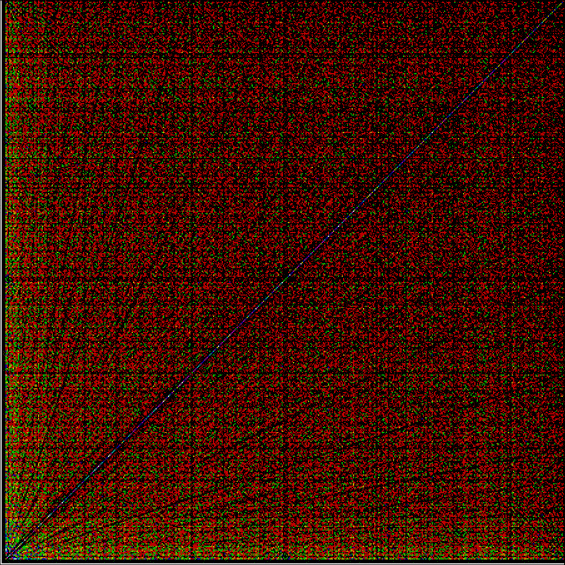
As any recreational mathematician kno, the Ulam spiral shows the prime numbers on a spiral grid of integers. Here’s a Ulam spiral with 1 represented in blue and 2, 3, 5, 7… as white blocks spiralling anti-clockwise from the right of 1:
The Ulam spiral of prime numbers
Ulam spiral at higher resolution
I like the Ulam spiral and whenever I’m looking at new number sequences I like to Ulamize it, that is, display it on a spiral grid of integers. Sometimes the result looks good, sometimes it doesn’t. But I’ve always wondered something beforehand: will this be the spiral where I see a message appear? That is, will I see a message from Mater Mathematica, Mother Maths, the omniregnant goddess of mathematics? Is there an image or text embedded in some obscure number sequence, revealed when the sequence is Ulamized and proving that there’s divine intelligence and design behind the universe? Maybe the image of a pantocratic cat will appear. Or a text in Latin or Sanskrit or some other suitably century-sanctified language.
That’s what I wonder. I don’t wonder it seriously, of course, but I do wonder it. But until 22nd March 2025 I’d never seen any Ulam-ish spiral that looked remotely like a message. But 22nd May is the day I Ulamed some continued fractions. And I saw something that did look a little like a message. Like text, that is. But I might need to explain continued fractions first. What are they? They’re a fascinating and beautiful way of representing both rational and irrational numbers. The continued fractions for rational numbers look like this in expanded and compact format:
5/3 = 1 + 1/(1 + ½) = 1 + ⅔
5/3 = [1; 1, 2]
19/7 = 2 + 1/(1 + 1/(2 + ½)) = 2 + 4/7
19/7 = [2; 1, 2, 2]
2/3 = 0 + 1/(1 + 1/2)
2/3 = [0; 1, 2] (compare 5/3 above)
3/5 = 0 + 1/(1 + 1/(1 + 1/2))
3/5 = [0; 1, 1, 2]
5/7 = 0 + 1/(1 + 1/(2 + 1/2))
5/7 = [0; 1, 2, 2] (compare 19/7 above)
13/17 = 0 + 1/(1 + 1/(3 + 1/4))
13/17 = [0; 1, 3, 4]
30/67 = 0 + 1/(2 + 1/(4 + 1/(3 + ½)))
30/67 = [0; 2, 4, 3, 2]
The continued fractions of irrational numbers are different. Most importantly, they never end. For example, here are the infinite continued fractions for φ, √2 and π in expanded and compact format:
φ = 1 + (1/(1 + 1/(1 + 1/(1 + …)))φ = [1; 1]
√2 = 1 + (1/(2 + 1/(2 + 1/(2 + …)))
√2 = [1; 2]
π = 3 + 1/(7 + 1/(15 + 1/(1 + 1/(292 + 1/(1 + 1/(1 + 1/(1 + 1/(2 + 1/(1 + 1/(3 +…))))))))))
π = [3; 7, 15, 1, 292, 1, 1, 1, 2, 1, 3…]
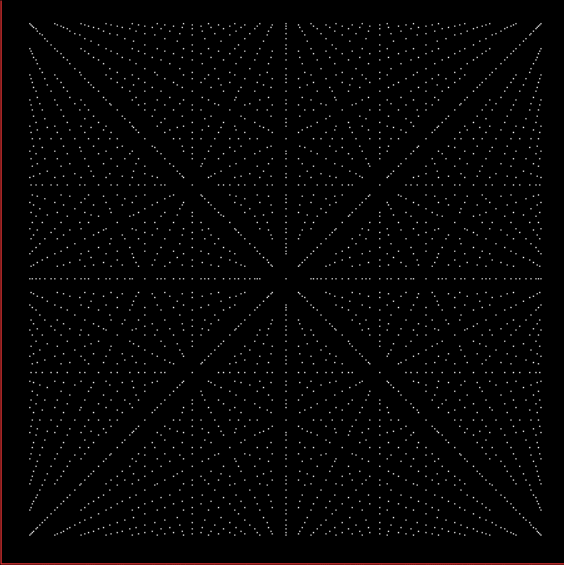
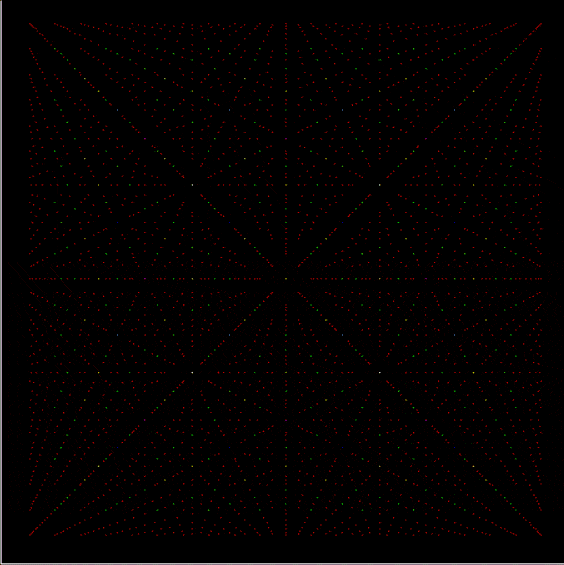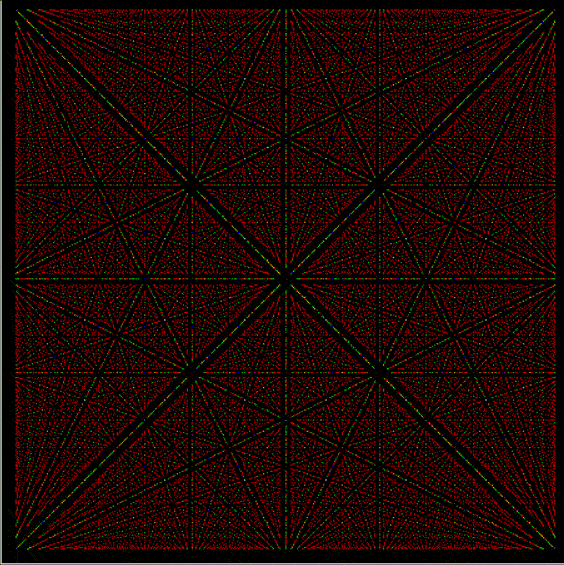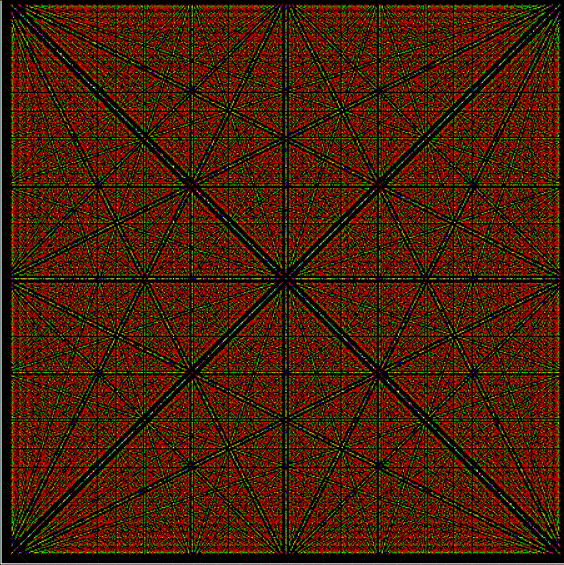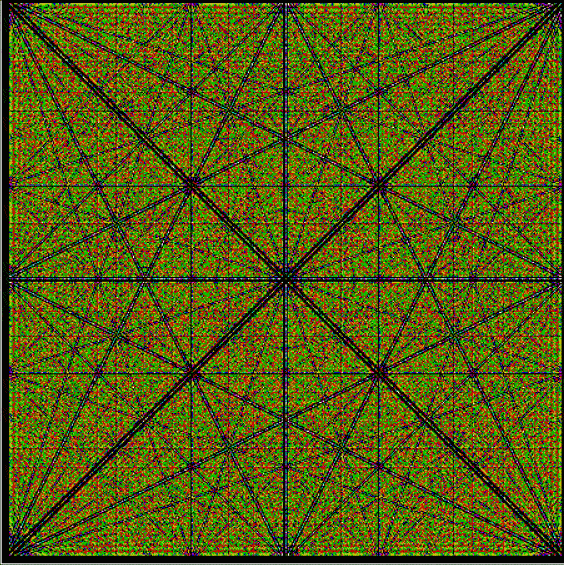
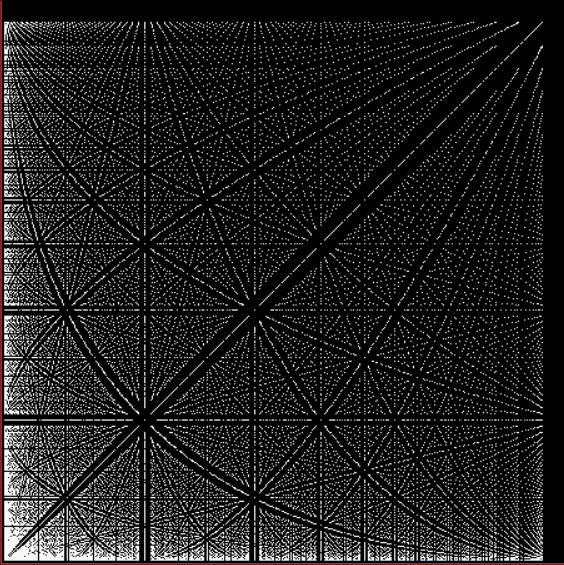
As you can see, the continued fraction of π doesn’t fall into a predictable pattern like those for φ and √2. But I’ve already gone into continued fractions further than I need for this post, so let’s return to the continued fractions of rationals. I set up an Ulam spiral to show patterns based on the continued fractions for 1/1, ½, ⅓, ⅔, 1/4, 2/4, 3/4, 1/5, 2/5, 3/5, 4/5, 1/6, 2/6, 3/6… (where the fractions are assigned to 1,2,3… and 2/4 = ½, 2/6 = ⅓ etc). For example, if the continued fraction contains a number higher than 5, you get this spiral:
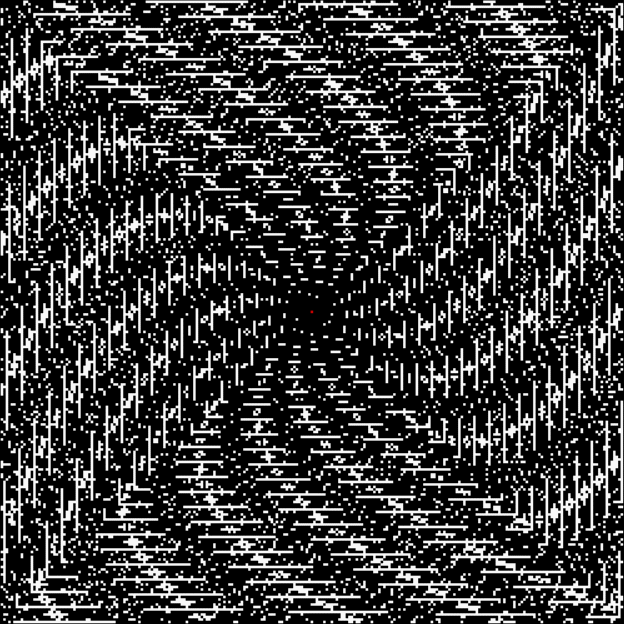
Spiral for continued fractions containing at least number > 5
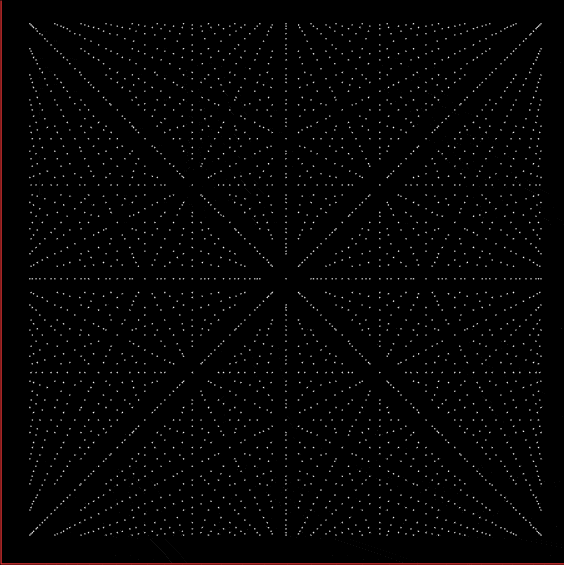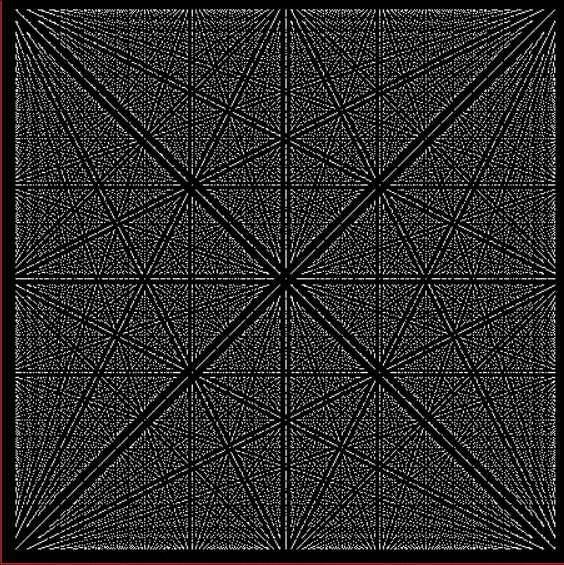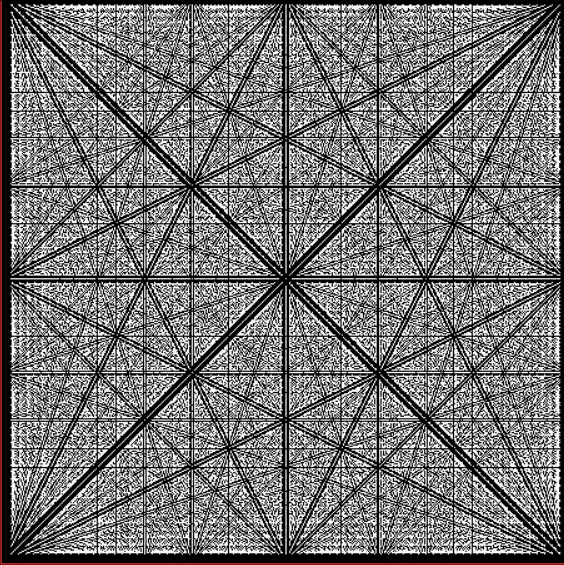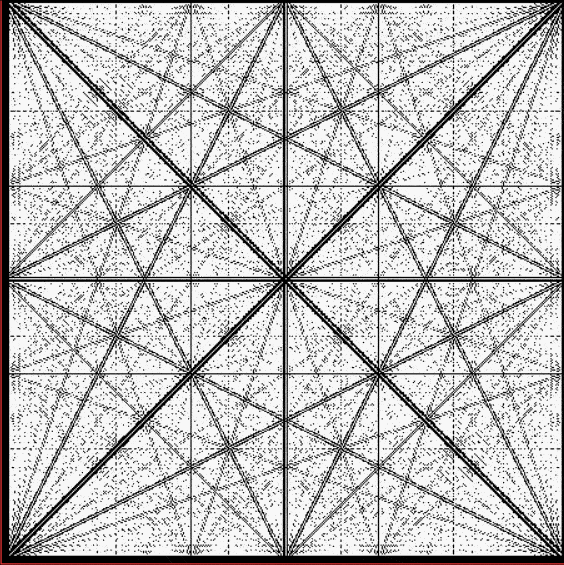
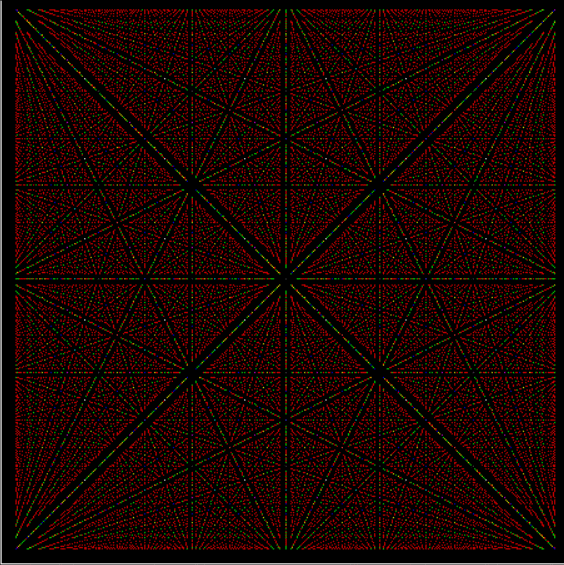
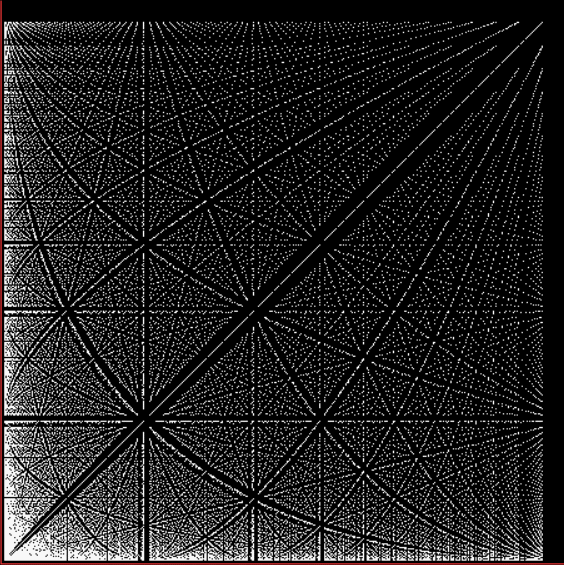
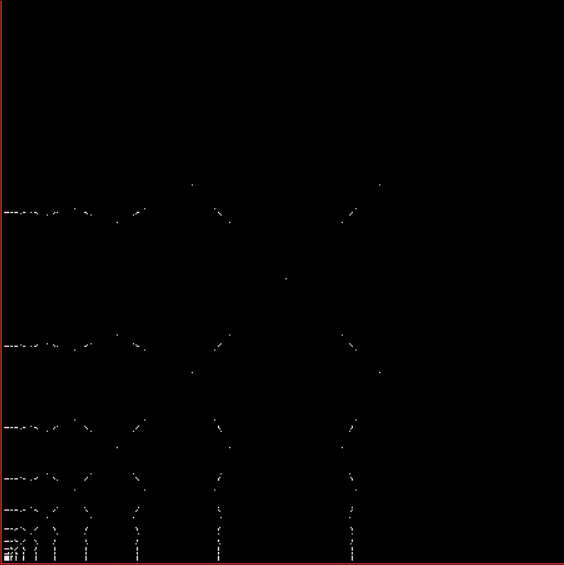
With tests for higher and higher numbers in the continued fractions, the spirals start to thin and apparent symbols start to appear in the arms of the spirals:
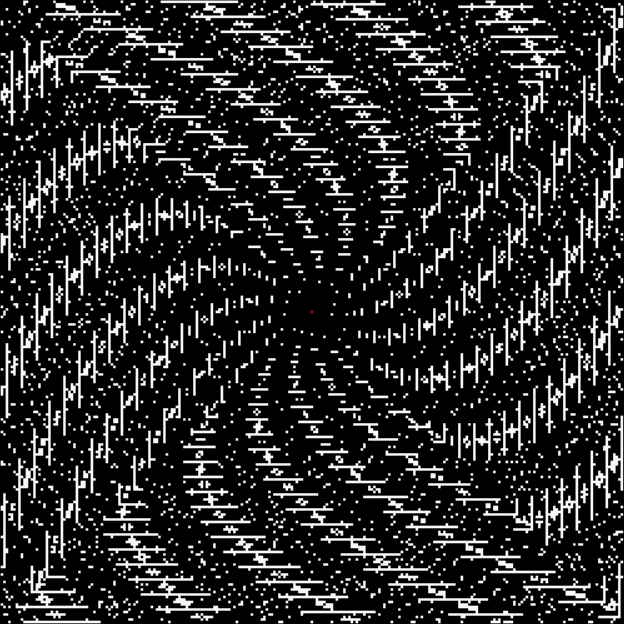
Spiral for contfrac > 10
Spiral for contfrac > 15
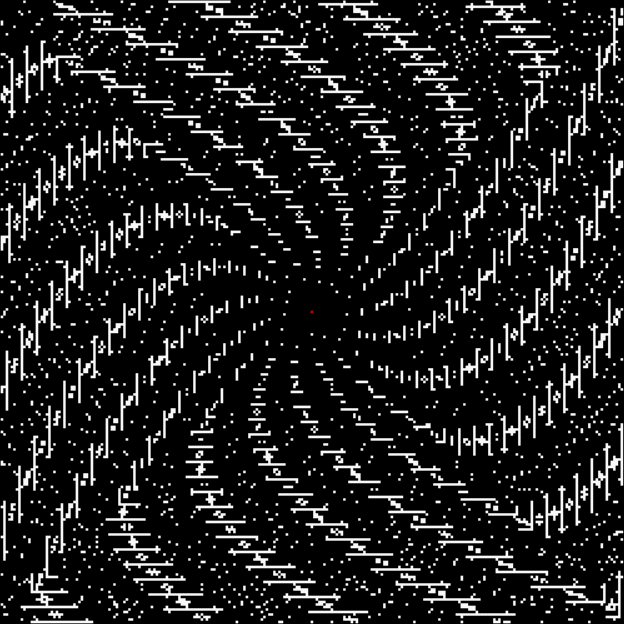
Spiral for contfrac > 20
Spiral for contfrac > 25
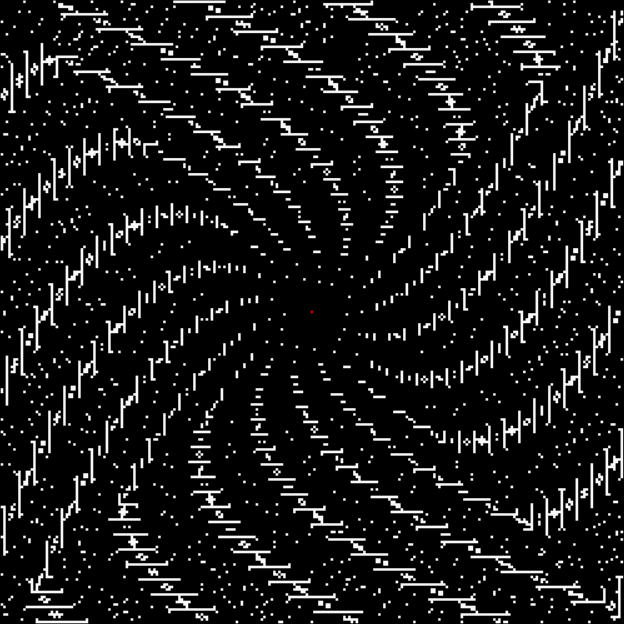
Spiral for contfrac > 30
Spiral for contfrac > 35
Spiral for contfrac > 40
Spirals for contfrac > 5..40 (animated at EZgif)
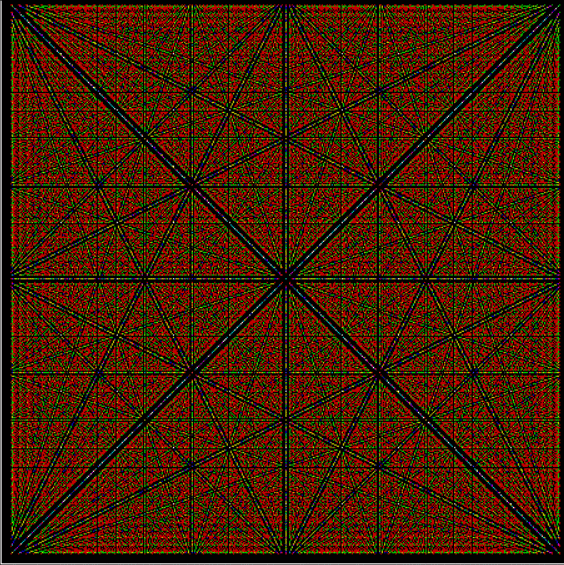
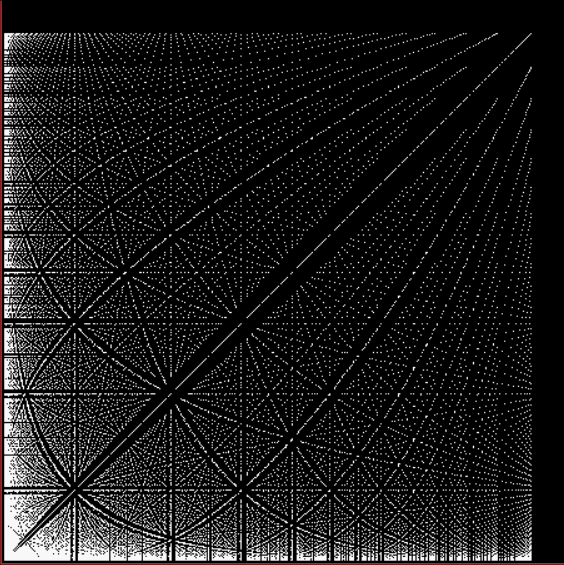
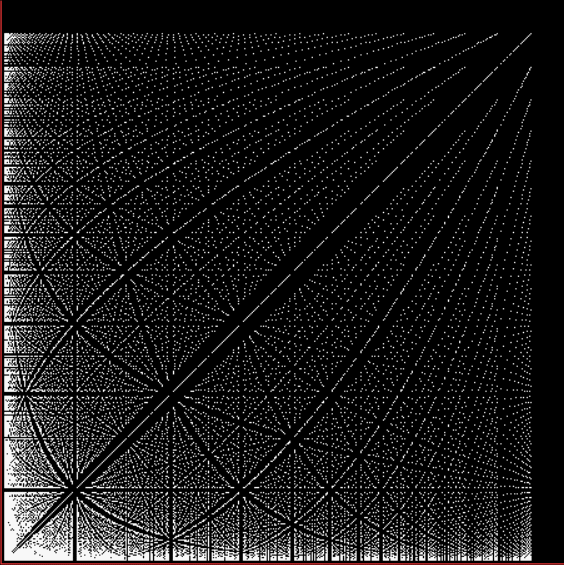
Here are some more of these spirals at increasing magnification:
Spiral for contfrac > 23 (#1)
Spiral for contfrac > 23 (#2)
Spiral for contfrac > 23 (#3)
Spiral for contfrac > 13
Spiral for contfrac > 15 (off-center)
Spiral for contfrac > 23 (off-center)
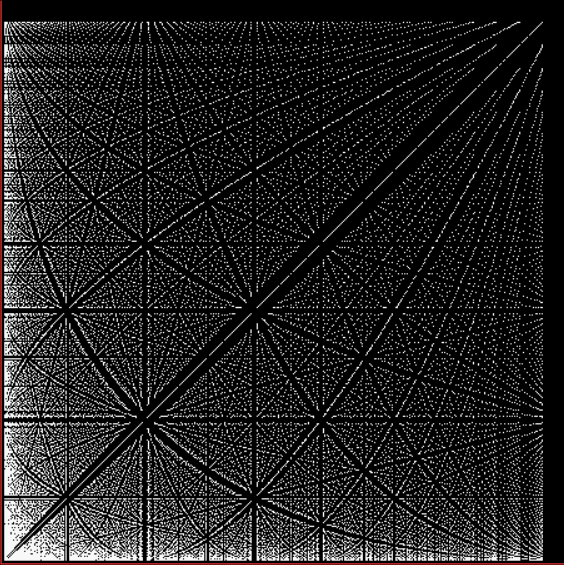
And here are some of the symbols picked out in blue:
Spiral for contfrac > 15 (blue symbols)
Spiral for contfrac > 23 (blue symbols)
But they’re not really symbols, of course. They’re quasi-symbols, artefacts of the Ulamization of a simple test on continued fractions. Still, they’re the closest I’ve got so far to a message from Mater Mathematica.
Overlord In Terms of Core Issues Around Maximal Engagement with Key Notions of the Über-Feral 