Portrayal of a pike, Esox lucius, by Norman Weaver (1913-89) on the cover of Fred Buller’s book about pike-fishing
If a person conceives an opinion
That my verses are stuff that will wash,
Or my Muse has one plume on her pinion,
That person’s opinion is bosh.
My philosophy, politics, free-thought!
Are worth not three skips of a flea,
And the emptiest thoughts that can be thought
Are mine on the sea.
In a maze of monotonous murmur
Where reason roves ruined by rhyme,
In a voice neither graver nor firmer
Than the bells on a fool’s cap chime,
A party pretentiously pensive,
With a Muse that deserves to be skinned,
Makes language and metre offensive
With rhymes on the wind.
A perennial procession of phrases
Pranked primly, though pruriently prime,
Precipitates preachings on praises
In a ruffianly riot of rhyme
Through the pressure of print on my pages:
But reckless the reader must be
Who imagines me one of the sages
That steer through Time’s sea.
Mad mixtures of Frenchified offal
With insults to Christendom’s creed,
Blind blasphemy, schoolboylike scoff, all
These blazon me blockhead indeed.
I conceive myself obviously some one
Whose audience will never be thinned,
But the pupil must needs be a rum one
Whose teacher is wind.
In my poems, with ravishing rapture
Storm strikes me and strokes me and stings:
But I’m scarcely the bird you might capture
Out of doors in the thick of such things.
I prefer to be well out of harm’s way
When tempest makes tremble the tree,
And the wind with omnipotent arm-sway
Makes soap of the sea.
Hanging hard on the rent rags of others,
Who before me did better, I try
To believe them my sisters and brothers,
Though I know what a low lot am I.
The mere sight of a church sets me yelping
Like a boy that at football is shinned!
But the cause must indeed be past helping
Whose gospel is wind.
All the pale past’s red record of history
Is dusty with damnable deeds;
But the future’s mild motherly mystery
Peers pure of all crowns and all creeds.
Truth dawns on time’s resonant ruin,
Frank, fulminant, fragrant, and free:
And apparently this is the doing
Of wind on the sea.
Fame flutters in front of pretension
Whose flagstaff is flagrantly fine:
And it cannot be needful to mention
That such beyond question is mine.
Some singers indulging in curses,
Though sinful, have splendidly sinned:
But my would-be maleficent verses
Are nothing but wind.
• Algernon Charles Swinburne viâ Pseudopodium
Elsewhere Other-Accessible…
• Swinburne on Swinburne — “Poeta Loquitur” at Mind of Winter
It’s an interesting little exercise in elementary trigonometry to turn the Sierpiński triangle…
A Sierpiński triangle
…into its circular equivalent:
A Sierpiński trisc
You could call that a trisc, because it’s a triangle turned into a disc. And here’s triangle-and-trisc in one image:
Sierpiński triangle + Sierpiński trisc
But what’s the square equivalent of a Sierpiński triangle? This is:
Square from Sierpiński triangle
You can do that directly, as it were:
Sierpiński triangle → square
Or you can convert the triangle into a disc, then the disc into a square, like this:
Sierpiński triangle → trisc → square
Now try converting the triangle into a pentagon:
Pentagon from Sierpiński triangle
Sierpiński triangle → pentagon
Sierpiński triangle → trisc → pentagon
And a hexagon:
Hexagon from Sierpiński triangle
Sierpiński triangle → hexagon
Sierpiński triangle → trisc → hexagon
But you can also convert the Sierpiński trisc back into a Sierpiński triangle, then into a Sierpiński trisc again:
Sierpiński triangle → trisc → triangle → trisc
Sierpiński triangle → trisc → triangle → trisc (animated at Ezgif)
Sierpiński triangle → trisc → triangle → trisc (b&w)
Sierpiński triangle → trisc → triangle → trisc (b&w) (animated at Ezgif)
After triangles come squares. Here’s a shape called a T-square fractal:
And here’s the circular equivalent of a T-square fractal:
T-square fractal → T-squisc
T-square fractal + T-squisc
If a disc from a triangle is a trisc, then a disc from a square is a squisc (it would be pentisc, hexisc, heptisc for pentagonal, hexagonal and heptagonal fractals). Here’s the octagonal equivalent of a T-square fractal:
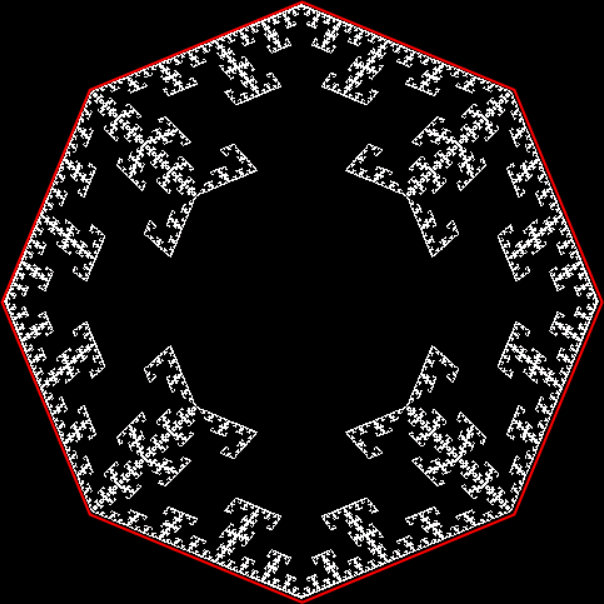
Octagon from T-square fractal
As with the Sierpiński trisc, you can use the T-squisc to create the T-octagon:
T-square fractal → T-squisc → T-octagon (color)
Or you can convert the T-square directly into the T-octagon:
T-square fractal to T-octagon fractal
But using the squisc makes for interesting multiple images:
T-square fractal → T-squisc → T-octagon (b&w)
T-square fractal → T-squisc → T-octagon → T-squisc
T-square fractal → T-squisc → T-octagon → T-squisc (animated at Ezgif)
The conversions from polygon to polygon look best when the number of sides in the higher polygon are a multiple of the number of sides in the lower, like this:
Sierpiński triangle → Sierpiński hexagon → Sierpiński nonagon
Overlord In Terms of Core Issues Around Maximal Engagement with Key Notions of the Über-Feral 