Category Archives: Mathematics

Factory Façades

by in Arithmetic, Mathematics and tagged , , , , , , | Leave a comment

Practically speaking, I’d never heard of them. Practical numbers, that is. They’re defined like this at the Online Encyclopedia of Integer Sequences:

A005153 Practical numbers: positive integers m such that every k <= sigma(m) is a sum of distinct divisors of m. Also called panarithmic numbers. […] Equivalently, positive integers m such that every number k <= m is a sum of distinct divisors of m. — A005153 at OEIS

In other words, if you take, say, divisors(12) = 1, 2, 3, 4, 6, you can find partial sums of those divisors that equal every number from 1 to 16, where 16 = 1+2+3+4+6. Here are all those sums, with c as the count of divisor-sums equalling a particular k (to simplify things, I’m excluding 12 as a divisor of 12):

1, 2, 3, 4, 6 = divisors(12)

01 = 1 (c=1)
02 = 2 (c=1)
03 = 1 + 2 = 3 (c=2)
04 = 1 + 3 = 4 (c=2)
05 = 2 + 3 = 1 + 4 (c=2)
06 = 1 + 2 + 3 = 2 + 4 = 6 (c=3)
07 = 1 + 2 + 4 = 3 + 4 = 1 + 6 (c=3)
08 = 1 + 3 + 4 = 2 + 6 (c=2)
09 = 2 + 3 + 4 = 1 + 2 + 6 = 3 + 6 (c=3)
10 = 1 + 2 + 3 + 4 = 1 + 3 + 6 = 4 + 6 (c=3)
11 = 2 + 3 + 6 = 1 + 4 + 6 (c=2)
12 = 1 + 2 + 3 + 6 = 2 + 4 + 6 (c=2)
13 = 1 + 2 + 4 + 6 = 3 + 4 + 6 (c=2)
14 = 1 + 3 + 4 + 6 (c=1)
15 = 2 + 3 + 4 + 6 (c=1)
16 = 1 + 2 + 3 + 4 + 6 (c=1)

Learning about practical numbers inspired me to look at the graphs of the count of the divisor-sums for 12. If you include count(0) = 1 (there is one way of choosing divisors of 12 to equal 0, namely, by choosing none of the divisors), the graph looks like this:

counts of divisorsum(12) = k, where 12 = 2^2 * 3 → 1, 2, 3, 4, 6

Here are some more graphs for partialsumcount(n), adjusted for a standardized y-max. They remind me variously of skyscrapers, pyramids, stupas, factories and factory façades, forts bristling with radar antennae, and the Houses of Parliament. All in an art-deco style:

18 = 2 * 3^2 → 1, 2, 3, 6, 9

24 = 2^3 * 3 → 1, 2, 3, 4, 6, 8, 12

30 = 2 * 3 * 5 → 1, 2, 3, 5, 6, 10, 15

36 = 2^2 * 3^2 → 1, 2, 3, 4, 6, 9, 12, 18

48 = 2^4 * 3 → 1, 2, 3, 4, 6, 8, 12, 16, 24

54 = 2 * 3^3 → 1, 2, 3, 6, 9, 18, 27

60 = 2^2 * 3 * 5 → 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30

72 = 2^3 * 3^2 → 1, 2, 3, 4, 6, 8, 9, 12, 18, 24, 36

88 = 2^3 * 11 → 1, 2, 4, 8, 11, 22, 44, 88

96 = 2^5 * 3 → 1, 2, 3, 4, 6, 8, 12, 16, 24, 32, 48

100 = 2^2 * 5^2 → 1, 2, 4, 5, 10, 20, 25, 50

108 = 2^2 * 3^3 → 1, 2, 3, 4, 6, 9, 12, 18, 27, 36, 54

120 = 2^3 * 3 * 5 → 1, 2, 3, 4, 5, 6, 8, 10, 12, 15, 20, 24, 30, 40, 60

126 = 2 * 3^2 * 7 → 1, 2, 3, 6, 7, 9, 14, 18, 21, 42, 63

162 = 2 * 3^4 → 1, 2, 3, 6, 9, 18, 27, 54, 81

220 = 2^2 * 5 * 11 → 1, 2, 4, 5, 10, 11, 20, 22, 44, 55, 110

And what about im-practical numbers, where the partial sums of divisors(m) don’t equal every number 1..sigma(m)? There are interesting fractal patterns to be uncovered there, as you can see from the graph for 190 (because all divsumcount(k) = 1, the graph looks like a bar-code):

190 = 2 * 5 * 19 → 1, 2, 5, 10, 19, 38, 95

Sorted for D’s nand Wizz

by in Geometry, Mathematics, Polygonal numbers, Squares, Triangular Numbers and tagged , , , , | Leave a comment

As I’ve pre-previously pointed out, there are an infinite number of points in the plane. And in part of the plane. So you have to pare points to create interesting shapes. One way of paring points is by comparing them. After you’ve compared them, you can sort them. For example, you can compare the distance from (x,y) to the four vertices of a square. Then you can sort the distances from nearest to furthest. Then you can mark (x,y) if the distance to, say, the nearest vertice from (x,y) is evenly divisible by 2 when measured in pixels or some other unit. When you do that, you might get an image like this (depending on the hardware and software you use):

Distance to nearest vertex is evenly divisible by 2, i.e. d mod 2 = 0 for v1 (vertices marked in red)

Or you can mark (x,y) if the distance to the nearest vertex is a triangular number:

is_triangular(d) for v1

Or a square number:

is_square(d) for v1

Or you can test the distance to the second-nearest vertex:

d mod 2 = 0 for v2

And the third-nearest (or second-furthest) vertex:

d mod 2 = 0 for v3

And furthest vertex:

d mod 2 = 0 for v4

Now try expanding or contracting the square:

d mod 2 = 0 for v1 on square * 2

d mod 2 = 0 for v1 on square * 3

d mod 2 = 0 for v1 on square * 0.5

d mod 2 = 0 for v1 on square * 1.5

d mod 2 = 0 for v1 on square * 5

d mod 2 = 0 for v1 on square * 20

d mod 2 = 0 for v1 on square * 100

Finally, here are some more mandala-like images created by using various d mod m on an expanded square (the images should be horizontally and vertically mirror-symmetrical, but my software introduced artefacts):

d mod 2 = 0 for v1 on square * 200
(open in separate window for better detail)

d mod 3 = 0 for v1 on square * 200

d mod 4 = 0 for v1 on square * 200

d mod 5 = 0 for v1 on square * 200

d mod 6 = 0 for v1 on square * 200

d mod 7 = 0 for p1 on square * 200

d mod 8 = 0 for p1 on square * 200

d mod 9 = 0 for p1 on square * 200

d mod 2..9 = 0 for p1 on square * 200 (animated at EZgif)

Post-Performative Post-Scriptum…

The title of this incendiary intervention is a paronomasia on “Sorted for E’s and Wizz”, a song offa of 1995 album Different Class by Sheffield Brit-popsters Pulp rebelliously referencing counter-cultural consumption of psychoactive drugs ecstasy and amphetamine. My program sorted distances, i.e. d’s, but not wizz, therefore it sorted d’s and-not wizz. In Boolean logic, nand means “and-not” (roughly speaking).

Previously Pre-Posted (Please Peruse)…

• Points Pared — an earlier look at points and polygons

Fertile Fractions

by in Arithmetic, Egyptian Fractions, Mathematics, Reciprocals and tagged , , | Leave a comment

Here’s the simplest possible Egyptian fraction summing to 1:

1 = 1/2 + 1/3 + 1/6 = egypt(2,3,6)

But how many times does 1 = egypt()? Infinitely often, as is very easy to prove. Take this equation:

1/6 – 1/7 = 1/42

For any 1/n, 1/n – 1/(n+1) = 1/(n*(n+1)) = 1/(n^2 + n). In the case of 1/6, the formula means that you can re-write egypt(2,3,6) like this:

1 = egypt(2,3,7,42) = 1/2 + 1/3 + 1/7 + 1/42

Now try these equations:

1/6 – 1/8 = 1/24
1/6 – 1/9 = 1/18
1/6 – 1/10 = 1/15

Which lead to these re-writes of egypt(2,3,6):

1 = egypt(2,3,8,24)
1 = egypt(2,3,9,18)
1 = egypt(2,3,10,15)

Alternatively, you can expand the 1/3 of egypt(2,3,6):

1/3 – 1/4 = 1/12

Therefore:

1 = egypt(2,4,6,12)

And the 1/12 opens all these possibilities:

1/12 – 1/13 = 1/156 → 1 = egypt(2,4,6,13,156)
1/12 – 1/14 = 1/84 → 1 = egypt(2,4,6,14,84)
1/12 – 1/15 = 1/60 → 1 = egypt(2,4,6,15,60)
1/12 – 1/16 = 1/48 → 1 = egypt(2,4,6,16,48)
1/12 – 1/18 = 1/36 → 1 = egypt(2,4,6,18,36)
1/12 – 1/20 = 1/30 → 1 = egypt(2,4,6,20,30)
1/12 – 1/21 = 1/28 → 1 = egypt(2,4,6,21,28)

So you can expand an Egyptian fraction for ever. If you stick to expanding the 1/6 to 1/7 + 1/42, then the 1/42 to 1/43 + 1/1806 and so on, you get this:

1 = egypt(2,3,6)
1 = egypt(2,3,7,42)
1 = egypt(2,3,7,43,1806)
1 = egypt(2,3,7,43,1807,3263442)
1 = egypt(2,3,7,43,1807,3263443,10650056950806)
1 = egypt(2,3,7,43,1807,3263443,10650056950807,113423713055421844361000442)
1 = egypt(2,3,7,43,1807,3263443,10650056950807,113423713055421844361000443,12864938683278671740537145998360961546653259485195806)
1 = egypt(2,3,7,43,1807,3263443,10650056950807,113423713055421844361000443,12864938683278671740537145998360961546653259485195807,165506647324519964198468195444439180017513152706377497841851388766535868639572406808911988131737645185442)
[…]

Elsewhere Other-Accessible…

• A000058, Sylvester’s Sequence, at the Online Encyclopedia of Integer Sequences, with more details on the numbers above

Feral Fractions

by in Mathematics, Base Behavior, Integer Sequences, Arithmetic, 666, Egyptian Fractions, Number of the Beast and tagged , , , , , | Leave a comment

“The uniquely unrepresentative ‘Egyptian’ fraction.” That’s what David Wells calls 2/3 = 0·666… in The Penguin Dictionary of Curious and Interesting Numbers (1986). Why unrepresentative”? Wells goes on to explain: “the Egyptians used only unit fractions, with this one exception. All other fractional quantities were expressed as sums of unit fractions.”

A unit fraction is 1 divided by a higher integer: 1/2, 1/3, 1/4, 1/5 and so on. Modern mathematicians are interested in those sums of unit fractions that produce integers, like this:

1 = 1/2 + 1/3 + 1/6 = egypt(2,3,6)
1 = 1/2 + 1/4 + 1/6 + 1/12 = egypt(2,4,6,12)
1 = 1/2 + 1/3 + 1/10 + 1/15 = = egypt(2,3,10,15)
1 = egypt(2,4,10,12,15)
1 = egypt(3,4,6,10,12,15)
1 = egypt(2,3,9,18)
1 = egypt(2,4,9,12,18)
1 = egypt(3,4,6,9,12,18)
1 = egypt(2,6,9,10,15,18)
1 = egypt(3,4,9,10,12,15,18)
1 = egypt(2,4,5,20)
1 = egypt(3,4,5,6,20)
1 = egypt(2,5,6,12,20)
1 = egypt(3,4,5,10,15,20)
1 = egypt(2,5,10,12,15,20)
1 = egypt(3,5,6,10,12,15,20)
1 = egypt(3,4,5,9,18,20)
1 = egypt(2,5,9,12,18,20)
1 = egypt(3,5,6,9,12,18,20)
1 = egypt(4,5,6,9,10,15,18,20)

2 = egypt(2,3,4,5,6,8,9,10,15,18,20,24)
2 = 1/2 + 1/3 + 1/4 + 1/5 + 1/6 + 1/8 + 1/9 + 1/10 + 1/15 + 1/18 + 1/20 + 1/24

Sums-to-integers like those are called Egyptian fractions, for short. I looked for some such sums that included 1/666:

1 = egypt(2,3,7,63,222,518,666)
1 = egypt(2,3,8,36,111,296,666)
1 = egypt(2,3,9,20,444,555,666)
1 = egypt(2,3,9,21,222,518,666)
1 = egypt(2,3,9,24,111,296,666)
1 = egypt(2,3,9,26,74,481,666)
1 = egypt(2,4,8,9,111,296,666)

And I looked for Egyptian fractions whose denominators summed to rep-digits like 111 and 666 (denominators are the bit below the stroke of 1/3 or 2/3, where the bit above is called the numerator):

1 = egypt(4,6,7,9,10,14,15,18,28)
111 = 4+6+7+9+10+14+15+18+28

1 = egypt(3,6,8,9,10,15,21,24,126)
222 = 3+6+8+9+10+15+21+24+126

1 = egypt(2,6,8,12,16,17,272)
333 = 2+6+8+12+16+17+272

1 = egypt(2,4,9,11,22,396)
444 = 2+4+9+11+22+396

1 = egypt(5,6,9,10,11,12,15,20,21,22,28,396)
555 = 5+6+9+10+11+12+15+20+21+22+28+396

1 = egypt(2,6,8,10,15,25,600)
666 = 2+6+8+10+15+25+600

1 = egypt(4,5,8,12,14,18,20,21,24,26,28,819)
999 = 4+5+8+12+14+18+20+21+24+26+28+819

Alas, Egyptian fractions like those are attractive but trivial. This isn’t trivial, though:

Prof Greg Martin of the University of British Columbia has found a remarkable Egyptian fraction for 1 with 454 denominators all less than 1000.

1 = egypt(97, 103, 109, 113, 127, 131, 137, 190, 192, 194, 195, 196, 198, 200, 203, 204, 205, 206, 207, 208, 209, 210, 212, 213, 214, 215, 216, 217, 218, 219, 220, 221, 225, 228, 230, 231, 234, 235, 238, 240, 244, 245, 248, 252, 253, 254, 255, 256, 259, 264, 265, 266, 267, 268, 272, 273, 274, 275, 279, 280, 282, 284, 285, 286, 287, 290, 291, 294, 295, 296, 299, 300, 301, 303, 304, 306, 308, 309, 312, 315, 319, 320, 321, 322, 323, 327, 328, 329, 330, 332, 333, 335, 338, 339, 341, 342, 344, 345, 348, 351, 352, 354, 357, 360, 363, 364, 365, 366, 369, 370, 371, 372, 374, 376, 377, 378, 380, 385, 387, 390, 391, 392, 395, 396, 399, 402, 403, 404, 405, 406, 408, 410, 411, 412, 414, 415, 416, 418, 420, 423, 424, 425, 426, 427, 428, 429, 430, 432, 434, 435, 437, 438, 440, 442, 445, 448, 450, 451, 452, 455, 456, 459, 460, 462, 464, 465, 468, 469, 470, 472, 473, 474, 475, 476, 477, 480, 481, 483, 484, 485, 486, 488, 490, 492, 493, 494, 495, 496, 497, 498, 504, 505, 506, 507, 508, 510, 511, 513, 515, 516, 517, 520, 522, 524, 525, 527, 528, 530, 531, 532, 533, 536, 539, 540, 546, 548, 549, 550, 551, 552, 553, 555, 558, 559, 560, 561, 564, 567, 568, 570, 572, 574, 575, 576, 580, 581, 582, 583, 584, 585, 588, 589, 590, 594, 595, 598, 603, 605, 608, 609, 610, 611, 612, 616, 618, 620, 621, 623, 624, 627, 630, 635, 636, 637, 638, 640, 642, 644, 645, 646, 648, 649, 650, 651, 654, 657, 658, 660, 663, 664, 665, 666, 667, 670, 671, 672, 675, 676, 678, 679, 680, 682, 684, 685, 688, 689, 690, 693, 696, 700, 702, 703, 704, 705, 707, 708, 710, 711, 712, 713, 714, 715, 720, 725, 726, 728, 730, 731, 735, 736, 740, 741, 742, 744, 748, 752, 754, 756, 759, 760, 762, 763, 765, 767, 768, 770, 774, 775, 776, 777, 780, 781, 782, 783, 784, 786, 790, 791, 792, 793, 798, 799, 800, 804, 805, 806, 808, 810, 812, 814, 816, 817, 819, 824, 825, 826, 828, 830, 832, 833, 836, 837, 840, 847, 848, 850, 851, 852, 854, 855, 856, 858, 860, 864, 868, 869, 870, 871, 872, 873, 874, 876, 880, 882, 884, 888, 890, 891, 893, 896, 897, 899, 900, 901, 903, 904, 909, 910, 912, 913, 915, 917, 918, 920, 923, 924, 925, 928, 930, 931, 935, 936, 938, 940, 944, 945, 946, 948, 949, 950, 952, 954, 957, 960, 962, 963, 966, 968, 969, 972, 975, 976, 979, 980, 981, 986, 987, 988, 989, 990, 992, 994, 996, 999) — "Egyptian Fractions" by Ron Knott at Surrey University

Color-Coded ContFracs

by in Arithmetic, Base Behavior, Continued Fractions, Mathematics and tagged , , , , , | Leave a comment

Continued fractions are cool… Too cool for school. Or too cool for my school, at least. Because I never learnt about them there. Now that I have learnt about them, they’ve helped me wade a little further into the immeasurable Mare Mathematicum. Or Mare Matris Mathematicæ. I’m almost ankle-deep now, rather than just toe-deep. (I wish.)

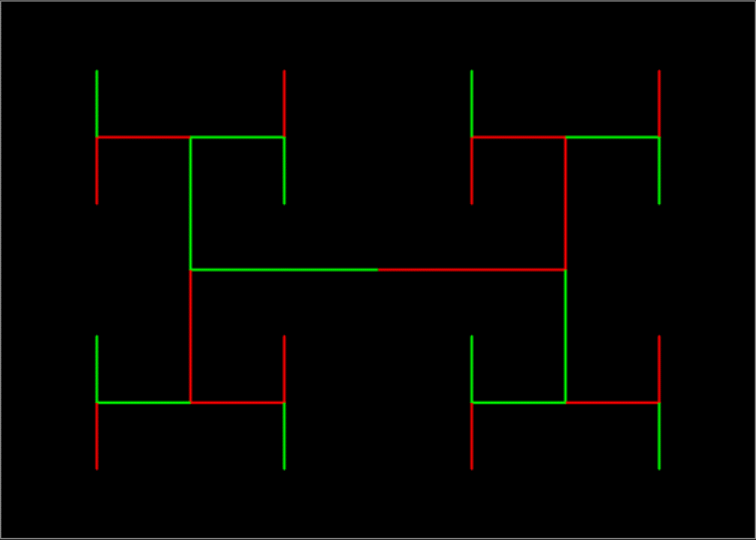
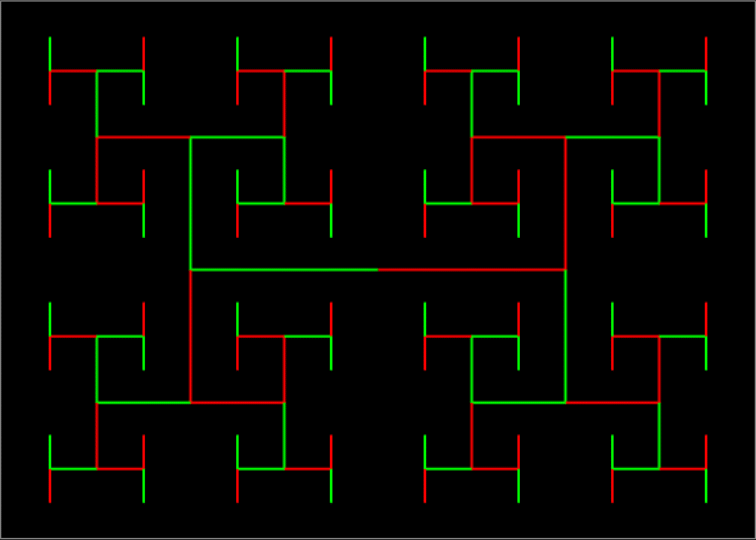
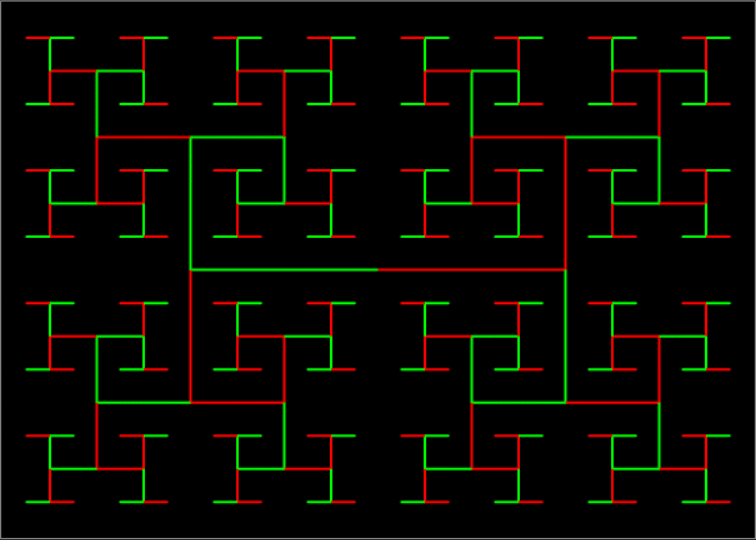
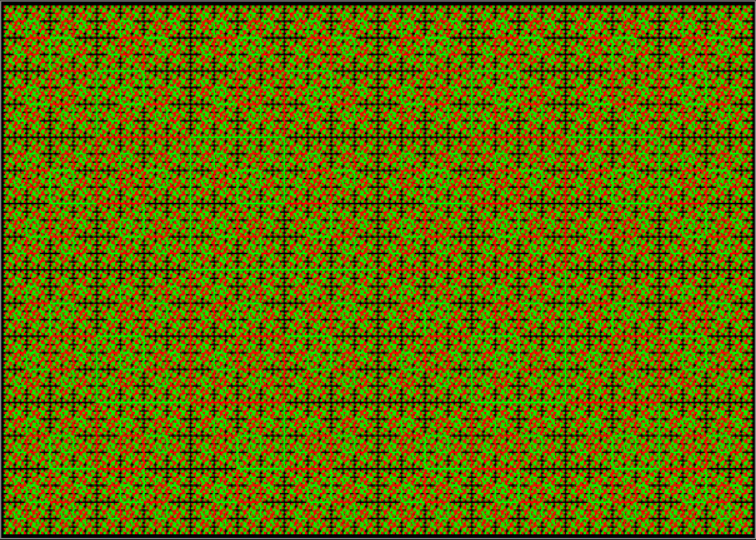
But apart from aiding my understanding, continued fractions have always enhanced my entertainment. I can use them to find pretty but (probably) puny patterns like these:


[3,1,2] = contfrac(3/12) in base 9 = contfrac(3/11) in base 10
4,1,3 ← 4/13 in b16 = 4/19
5,1,4 ← 5/14 in b25 = 5/29
6,1,5 ← 6/15 in b36 = 6/41
7,1,6 ← 7/16 in b49 = 7/55
8,1,7 ← 8/17 in b64 = 8/71
9,1,8 ← 9/18 in b81 = 9/89
A,1,9 ← A/19 in b100 = 10/109 → 10,1,9
B,1,A ← B/1A in b121 = 11/131 → 11,1,10
C,1,B ← C/1B in b144 = 12/155 → 12,1,11

Those patterns with square numbers carry on for ever, I assume. I also assume that the similar patterns below do too, though I’m not sure if every base contains an infinite number of them. Maybe some bases don’t contain any at all. I haven’t found any in base 10 so far:


[25,2] = contfrac(2/52) in base 9 = contfrac(2/47) in base 10 = [23,2]
42,1,3 ← 4/213 in b8 = 4/139 → 34,1,3
4,1,2,3,3 ← 41/233 in b8 = 33/155
24,1,3,1,2 ← 24/1312 in b5 = 14/207 → 14,1,3,1,2
1,17,1,2,3 ← 117/123 in b14 = 217/227 → 1,21,1,2,3
320,1,2 ← 3/2012 in b5 = 3/257 → 85,1,2
254,2 ← 2/542 in b7 = 2/275 → 137,2
3A,3 ← 3/A3 in b28 = 3/283 → 94,3
3,5,A,2 ← 35/A2 in b34 = 107/342 → 3,5,10,2
12,1,5,3 ← 12/153 in b17 = 19/377 → 19,1,5,3
12,1,5,3 ← 12/153 in b17 = 19/377 → 19,1,5,3
3,1,4,1,4,1,5 ← 314/1415 in b8 = 204/781
2,1,36,3,2 ← 213/632 in b12 = 303/902 → 2,1,42,3,2
3,2,11,2,2,2 ← 321/1222 in b9 = 262/911 → 3,2,10,2,2,2
41,2,1,1,6 ← 41/2116 in b8 = 33/1102 → 33,2,1,1,6
4H,4 ← 4/H4 in b65 = 4/1109 → 277,4
249,2 ← 2/492 in b17 = 2/1311 → 655,2
6,2,1,3,J ← 62/13J in b35 = 212/1349 → 6,2,1,3,19
8,3,3,1,D ← 83/31D in b22 = 179/1487 → 8,3,3,1,13
142,1,1,6 ← 14/2116 in b9 = 13/1554 → 119,1,1,6
10,1,111,1,1,2 ← 1011/11112 in b6 = 223/1556 → 6,1,43,1,1,2
204,1,17 ← 20/4117 in b8 = 16/2127 → 132,1,15
93,1,8 ← 9/318 in b27 = 9/2222 → 246,1,8
1,3A,1,1,4,2,2 ← 13A1/1422 in b12 = 2281/2330 → 1,46,1,1,4,2,2
4340,1,3 ← 4/34013 in b5 = 4/2383 → 595,1,3
13,1,7,6 ← 13/176 in b46 = 49/2444 → 49,1,7,6
C7,1,B ← C/71B in b21 = 12/3119 → 259,1,11
35,3,2,3,1,1,2 ← 353/23112 in b6 = 141/3284 → 23,3,2,3,1,1,2
1,2,2,1,O,F ← 122/1OF in b50 = 2602/3715 → 1,2,2,1,24,15
2,1,1,5,55 ← 211/555 in b28 = 1597/4065 → 2,1,1,5,145
1P,2,H,2 ← 1P/2H2 in b47 = 72/5219 → 72,2,17,2
50,14,1,1,1,5 ← 501/41115 in b6 = 181/5447 → 30,10,1,1,1,5
5450,1,4 ← 5/45014 in b6 = 5/6274 → 1254,1,4
3103,1,2 ← 3/10312 in b9 = 3/6815 → 2271,1,2
4B,1,2,2,C ← 4B/122C in b19 = 87/7631 → 87,1,2,2,12
3G,D,2,3 ← 3G/D23 in b26 = 94/8843 → 94,13,2,3
3,1,1,A,K,6 ← 311/AK6 in b29 = 2553/8996 → 3,1,1,10,20,6
1,2[70],1,3,9 ← 12[70]/139 in b98 = 9870/9907 → 1,266,1,3,9
14,1,9,A ← 14/19A in b97 = 101/10292 → 101,1,9,10
14,1,9,A ← 14/19A in b97 = 101/10292 → 101,1,9,10
4133,1,14,2 ← 41/331142 in b5 = 21/11422 → 543,1,9,2
1,E,4,1,M,7 ← 1E4/1M7 in b100 = 11404/12207 → 1,14,4,1,22,7
LG,5,4 ← L/G54 in b28 = 21/12688 → 604,5,4

Matching Fractions

by in Arithmetic, Base Behavior, Mathematics and tagged , , , , , , , , , , , | Leave a comment

0.1666… = 1/6
0.0273972… = 2/73
0.0379746… = 3/79
0.0016181229… = 1/618
0.0027322404… = 2/732 → 1/366
0.0058548009… = 5/854
0.01393354769… = 13/933
0.07598784194… = 75/987 → 25/329
0.08998988877… = 89/989
0.141993957703… = 141/993 → 47/331
0.0005854115443… = 5/8541
0.00129282482223… = 12/9282 → 2/1547
0.00349722279366… = 34/9722 → 17/4861
0.013599274705349… = 135/9927 → 15/1103
0.0000273205382146… = 2/73205

0.0465103… = 4/65 in base 8 = 4/53 in base 10
0.13735223… = 13/73 in b8 = 11/59 in b10
0.0036256353… = 3/625 → 1/207 in b8 = 3/405 → 1/135 in b10
0.01172160236… = 11/721 → 3/233 in b8 = 9/465 → 3/155 in b10
0.01272533117… = 12/725 in b8 = 10/469 in b10
0.03175523464… = 31/755 in b8 = 25/493 in b10
0.06776766655… = 67/767 in b8 = 55/503 in b10
0.251775771755… = 251/775 in b8 = 169/509 in b10
0.0003625152504… = 3/6251 in b8 = 3/3241 in b10
0.00137303402723… = 13/7303 in b8 = 11/3779 in b10
0.00267525714052… = 26/7525 in b8 = 22/3925 in b10
0.035777577356673… = 357/7757 in b8 = 239/4079 in b10

0.3763… = 3/7 in b9 = 3/7 in b10
0.0155187… = 1/55 in b9 = 1/50 in b10
0.0371482… = 3/71 in b9 = 3/64 in b10
0.0474627… = 4/74 in b9 = 4/67 in b10
0.43878684… = 43/87 in b9 = 39/79 in b10
0.07887877766… = 78/878 in b9 = 71/719 in b10
0.01708848667… = 17/0884 → 4/221 in b9 = 16/724 → 4/181 in b10
0.170884866767… = 170/884 → 40/221 in b9 = 144/724 → 36/181 in b10

0.2828… = 2/8 → 1/4 in b11 = 2/8 → 1/4 in b10
0.4986… = 4/9 in b11 = 4/9 in b10
0.54A9A8A6… = 54/A9 in b11 = 59/119 in b10
0.0010A17039… = 1/A17 in b11 = 1/1228 in b10
0.010A170392A… = 10/A17 in b11 = 11/1228 in b10
0.01AA5854872… = 1A/A58 in b11 = 21/1273 in b10
0.027A716A416… = 27/A71 in b11 = 29/1288 in b10
0.032A78032A7… = 32/A78 → 1/34 in b11 = 35/1295 → 1/37 in b10
0.0190AA5A829… = 19/0AA5 → 4/221 in b11 = 20/1325 → 4/265 in b10
0.190AA5A829… = 190/AA5 → 40/221 in b11 = 220/1325 → 44/265 in b10

0.23B7A334… = 23/B7 in b12 = 27/139 in b10
0.075BA597224… = 75/BA5 in b12 = 89/1709 in b10
0.0ABBABAAA99… = AB/BAB in b12 = 131/1715 in b10
0.185BB5B859B4… = 185/BB5 in b12 = 245/1721 in b10

Phascinating Phibonacci Phact Phor Phiday

by in Arithmetic, Fibonacci Sequence, Integer Sequences, φ, Mathematics, Phi and tagged , , , , , , , , | Leave a comment

Phiday falls on the 11th, 12th and 23rd of each month, because 11, 12 and 23 represent entries in the famous Fibonacci sequence:

1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946, 17711, 28657, 46368, 75025, 121393, 196418, 317811, 514229, 832040, 1346269, 2178309, 3524578, 5702887, 9227465, 14930352, 24157817, 39088169, 63245986, 102334155, 165580141, 267914296, 433494437, 701408733, 1134903170, 1836311903, 2971215073, 4807526976, 7778742049, 12586269025, 20365011074, 32951280099, 53316291173, 86267571272, 139583862445, 225851433717, 365435296162, 591286729879, 956722026041, 1548008755920, 2504730781961, 4052739537881, 6557470319842, 10610209857723, 17167680177565, 27777890035288, 44945570212853, 72723460248141, 117669030460994, 190392490709135, 308061521170129, 498454011879264, 806515533049393, 1304969544928657, …

Successive entries in the Fibonacci sequence provide better and better approximations to the golden ratio or φ = 1.61803398874989484820458683…

2 = 2/1
1.5 = 3/2
1.6 = 5/3
1.6 = 8/5
1.625 = 13/8
1.6153846… = 21/13
1.619047619… = 34/21
1.6176470588235294117647… = 55/34
1.618… = 89/55
1.617977528… = 144/89
1.61805… = 233/144
1.618025751… = 377/233
1.618037135… = 610/377
1.618032786… = 987/610
1.618034447… = 1597/987
1.618033813… = 2584/1597
1.618034055… = 4181/2584
1.618033963… = 6765/4181
1.618033998… = 10946/6765
1.618033985… = 17711/10946

Today is 23rd June, so here’s a Fascinating Fibonacci Fact for Phiday. First, list the rational fractions < 1 in simplified form and mark the Fibonacci fractions:

1/2, 1/3, 2/3, 1/4, 3/4, 1/5, 2/5, 3/5, 4/5, 1/6, 5/6, 1/7, 2/7, 3/7, 4/7, 5/7, 6/7, 1/8, 3/8, 5/8, 7/8, 1/9, 2/9, 4/9, 5/9, 7/9, 8/9, 1/10, 3/10, 7/10, 9/10, 1/11, 2/11, 3/11, 4/11, 5/11, 6/11, 7/11, 8/11, 9/11, 10/11, 1/12, 5/12, 7/12, 11/12, 1/13, 2/13, 3/13, 4/13, 5/13, 6/13, 7/13, 8/13, 9/13, 10/13, 11/13, 12/13, 1/14, 3/14, 5/14, 9/14, 11/14, 13/14, 1/15, 2/15, 4/15, 7/15, 8/15, 11/15, 13/15, 14/15, 1/16, 3/16, 5/16, 7/16, 9/16, 11/16, 13/16, 15/16, 1/17, 2/17, 3/17, 4/17, 5/17, 6/17, 7/17, 8/17, 9/17, 10/17, 11/17, 12/17, 13/17, 14/17, 15/17, 16/17, 1/18, 5/18, 7/18, 11/18, 13/18, 17/18, 1/19, 2/19, 3/19, 4/19, 5/19, 6/19, 7/19, 8/19, 9/19, 10/19, 11/19, 12/19, 13/19, 14/19, 15/19, 16/19, 17/19, 18/19, 1/20, 3/20, 7/20, 9/20, 11/20, 13/20, 17/20, 19/20, 1/21, 2/21, 4/21, 5/21, 8/21, 10/21, 11/21, 13/21, 16/21, 17/21, 19/21, 20/21, 1/22, 3/22, 5/22, 7/22, 9/22, 13/22, 15/22, 17/22, 19/22, 21/22, 1/23, 2/23, 3/23, 4/23, 5/23, 6/23, 7/23, 8/23, 9/23, 10/23, 11/23, 12/23, 13/23, 14/23, 15/23, 16/23, 17/23, 18/23, 19/23, 20/23, 21/23, 22/23…

Next, record the positions in the fraction list of the FibFracs, i.e. pos(fibonacci(i)/fibonacci(i+1)) = pos(fibfrac(i)):

1, 3, 8, 20, 53, 135, 353, 924, 2422, 6311, 16529, 43229, 113066, 296173, 775286, 2029661, 5313844, 13911391, 36419909, 95348490, 249624578, 653521015, 1710943906, 4479312193, 11726939926, 30701521655, 80377560978, 210431191133, 550915866198, 1442316294349, 3776032465954, 9885782372588, 25881314454327, 67758160822605, 177393168080718, 464421339906882, 1215870841639593, …

What do you get when you divide pos(fibfrac(i+1)) by pos(fibfrac(i))?

pos(1/2) = 1
pos(2/3) = 3 (3/1 = 3)
pos(3/5) = 8 (8/3 = 2.6…)
pos(5/8) = 20 (20/8 = 2.5)
pos(8/13) = 53 (53/20 = 2.65)
pos(13/21) = 135 (2.5471698113207…)
pos(21/34) = 353 (2.6148…)
pos(34/55) = 924 (2.617563739376770538243626062…)
pos(55/89) = 2422 (2.621…)
pos(89/144) = 6311 (2.605697770437654830718414533…)
pos(144/233) = 16529 (2.619077800665504674378070037…)
pos(233/377) = 43229 (2.615342730957710690301893642…)
pos(377/610) = 113066 (2.615512734506928219482291980…)
pos(610/987) = 296173 (2.619470044045071020465922559…)
pos(987/1597) = 775286 (2.617679531895209894217231145…)
pos(1597/2584) = 2029661 (2.617951310871084993150914630…)
pos(2584/4181) = 5313844 (2.618094351716863062353762525…)
pos(4181/6765) = 13911391 (2.617952465296309037299551888…)
pos(6765/10946) = 36419909 (2.617991903182075753603647543…)
pos(10946/17711) = 95348490 (2.618032076906068051954770123…)
pos(17711/28657) = 249624578 (2.618023400265699016313735016…)
pos(28657/46368) = 653521015 (2.618015502463863954934758067…)
pos(46368/75025) = 1710943906 (2.618039614227248683043497844…)
pos(75025/121393) = 4479312193 (2.618035680358535377956453004…)
pos(121393/196418) = 11726939926 (2.618022459860278821159630657…)
pos(196418/317811) = 30701521655 (2.618033506501651708043379296…)
pos(317811/514229) = 80377560978 (2.618031831816708695313688353…)
pos(514229/832040) = 210431191133 (2.618034045479393794998913484…)
pos(832040/1346269) = 550915866198 (2.618033302153394031845776103…)
pos(1346269/2178309) = 1442316294349 (2.618033683260502304564996035…)
pos(2178309/3524578) = 3776032465954 (2.618033562227999267671331082…)
pos(3524578/5702887) = 9885782372588 (2.618034262608066669117450079…)
pos(5702887/9227465) = 25881314454327 (2.618034008728793003503058474…)
pos(9227465/14930352) = 67758160822605 (2.618033985181798482654668954…)
pos(14930352/24157817) = 177393168080718 (2.618033989221521810752093192…)
pos(24157817/39088169) = 464421339906882 (2.618033969017113072183685603…)
pos(39088169/63245986) = 1215870841639593 (2.618033964338027806153843993…)
[…]

In other words, pos(fibfrac(i+1)) / pos(fibfrac(i)) → φ^2 = 2.61803398874989484820458683… = φ + 1

Previously Pre-Posted (Please Peruse)

• Friday is Φiday

I Like Gryke

by in Arithmetic, Fractals, Geometry, Mathematics and tagged , , , , , , , , , , , , , , , , , , , , , | Leave a comment

Sometimes I find fractals. And sometimes fractals find me. Here’s a fractal that found me:

Limestone fractal #1

I call it a limestone fractal or pavement fractal or gryke fractal, because it reminds me of the fissured patterns you see in the limestone pavements of the Yorkshire Dales:

Fissured limestone pavement, Yorkshire Dales (Wikipedia)

The limestone blocks are called clints and the larger fissures between them are called grykes, with kamenitza and karren (from Slavic and German, respectively) for smaller pits and grooves:

Limestone linguistics (Dales Rocks)

Here’s the me-finding fractal again, in a slightly different version:

Limestone fractal #2

How did it find me? Well, I wasn’t looking for fractals, but looking at fractions. Farey fractions and Calkin-Wilf fractions, to be precise. They can both be represented as bifurcating trees, like this:

Calkin-Wilf tree (Wikipedia)

Both trees produce all the irreducible rational fractions — but in a different order. That’s why they create a fractal (rather than a 45° line). By following the same path in both bifurcating trees, I generated parallel sequences of Farey and Calkin-Wilf fractions, then used the Farey fractions to represent x in a 1×1 square and the Calkin-Wilf fractions to represent y (where the Calkin-Wilfs, a/b, were greater than 1, I simply a/b → b/a). When you do that (or use Stern-Brocot fractions instead of the Farey fractions), you get the limestone fractal.

I think it looks better in the second version (which is the one that found me, in fact). For LF #2, I was using standard binary numbers to generate the parallel sequences, so the leftmost digit was always 1 and final step of the tree-search was always in the same direction. Here’s LF #2 as black-on-white rather than white-on-black:

Limestone fractal #2 (black-on-white)

And here is the formation of LF #1 as an animated gif:

Growth of limestone fractal (animated at ezGIF)

And if that’s a me-finding fractal, what about me-found fractals? Here’s one:

The Hourglass Fractal (animated gif optimized at ezGIF)

Hourglass fractal

I can say “I found that fractal” because I was looking for fractals when it appeared on the screen. And re-appeared (and re-re-appeared), because I’ve found it using different methods.

Elsewhere Other-Accessible

• Hour Power — more on the hourglass fractal