It’s a very simple function that raises a very difficult question. An unanswered question, in fact. Take any whole number. If it’s odd, multiply it by 3 and add 1. If it’s even, divide it by 2. Repeat until you reach 1. That’s the hailstone function, because the numbers rise and fall like hailstones being formed in a cloud. Here are some examples:

5 → 16 → 8 → 4 → 2 → 1 (steps=5)

3 → 10 → 5 → 16 → 8 → 4 → 2 → 1 (st=7)

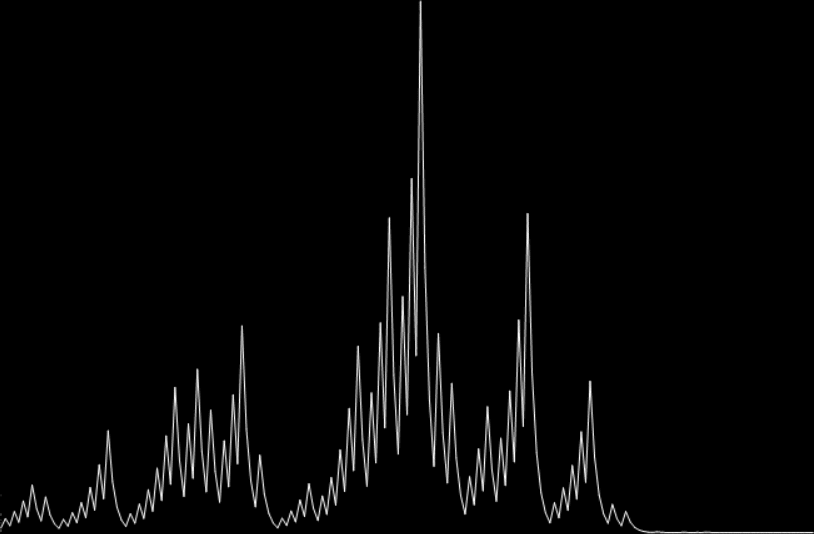
7 → 22 → 11 → 34 → 17 → 52 → 26 → 13 → 40 → 20 → 10 → 5 → 16 → 8 → 4 → 2 → 1 (st=16)

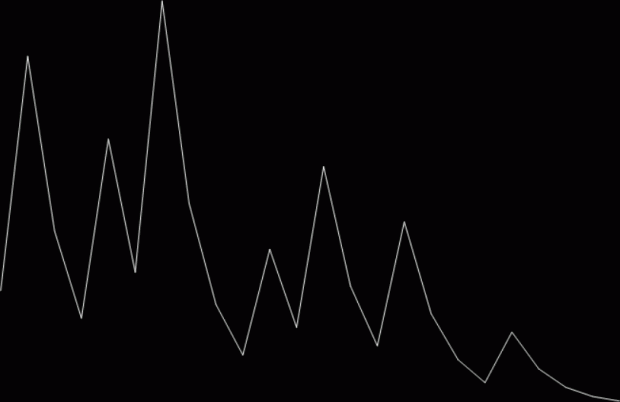
Graph for hail(7) = 16 (mx=52)

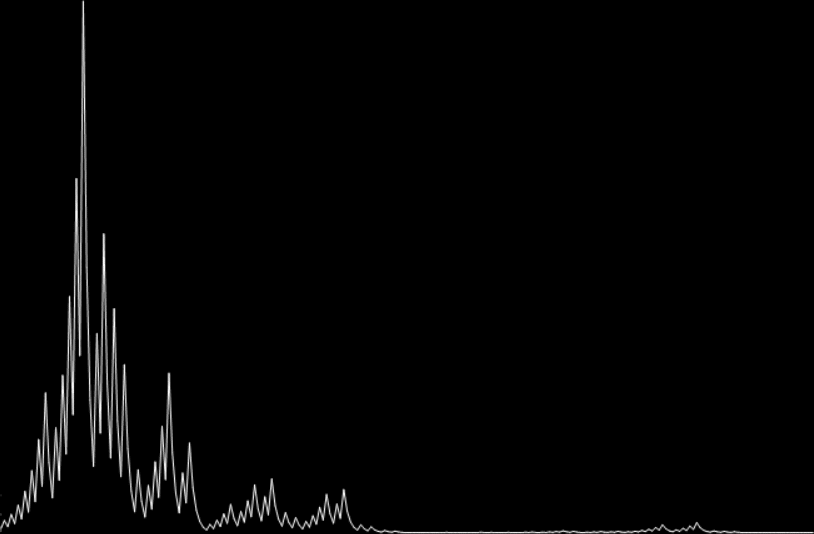
25 → 76 → 38 → 19 → 58 → 29 → 88 → 44 → 22 → 11 → 34 → 17 → 52 → 26 → 13 → 40 →
20 → 10 → 5 → 16 → 8 → 4 → 2 → 1 (st=23)

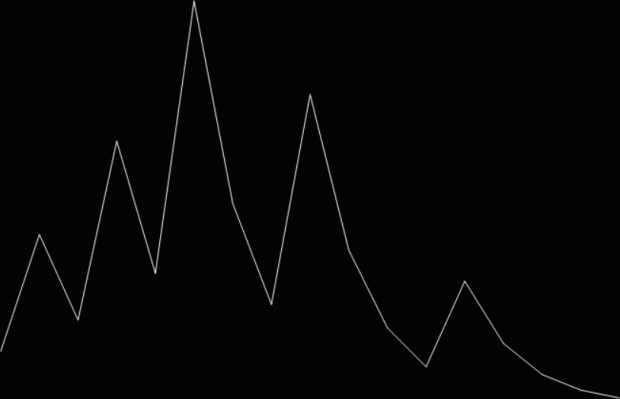
Graph for hail(25) = 23 (mx=88)

But is this function truly a hailstone function? That is, does every number fall finally to earth and reach 1? So far, for every number tested, the answer has been yes. But do all numbers reach 1? The Collatz conjecture says they do. But no-one can prove it. Or disprove it. All it would take is one number failing to fall to earth. Mathematicians don’t think there is one, but numbers can take a surprising length of time to get to the ground. Here’s 27:

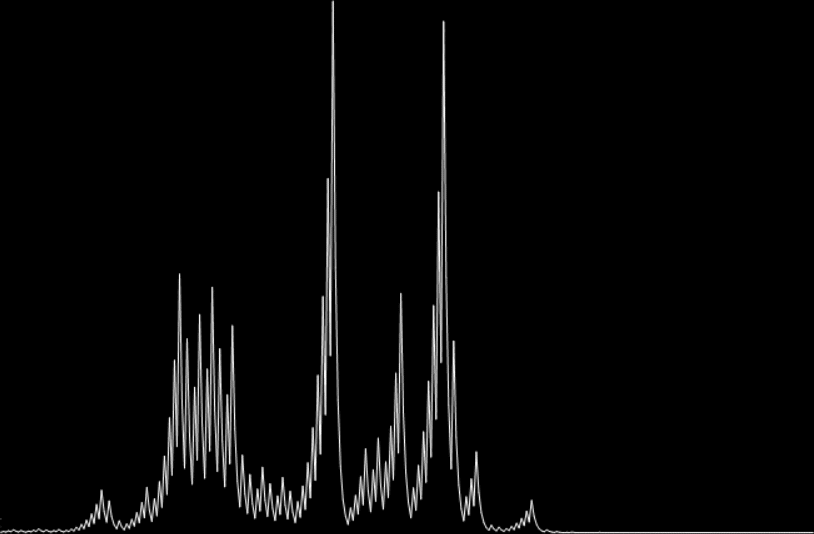
27 → 82 → 41 → 124 → 62 → 31 → 94 → 47 → 142 → 71 → 214 → 107 → 322 → 161 → 484 → 242 → 121 → 364 → 182 → 91 → 274 → 137 → 412 → 206 → 103 → 310 → 155 → 466 → 233 → 700 → 350 → 175 → 526 → 263 → 790 → 395 → 1186 → 593 → 1780 → 890 → 445 → 1336 → 668 → 334 → 167 → 502 → 251 → 754 → 377 → 1132 → 566 → 283 → 850 → 425 → 1276 → 638 → 319 → 958 → 479 → 1438 → 719 → 2158 → 1079 → 3238 → 1619 → 4858 → 2429 → 7288 → 3644 → 1822 → 911 → 2734 → 1367 → 4102 → 2051 → 6154 → 3077 → 9232 → 4616 → 2308 → 1154 → 577 → 1732 → 866 → 433 → 1300 → 650 → 325 → 976 → 488 → 244 → 122 → 61 → 184 → 92 → 46 → 23 → 70 → 35 → 106 → 53 → 160 → 80 → 40 → 20 → 10 → 5 → 16 → 8 → 4 → 2 → 1 (st=111)

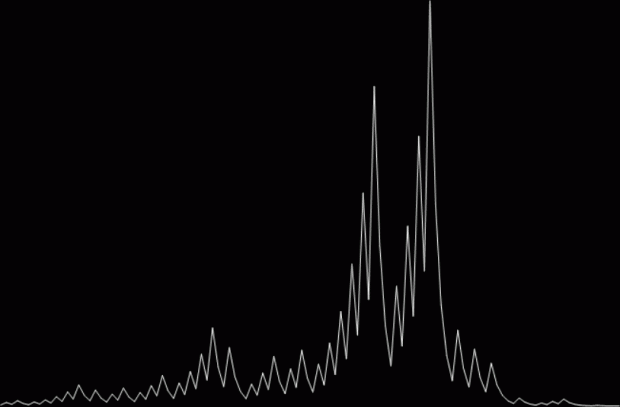
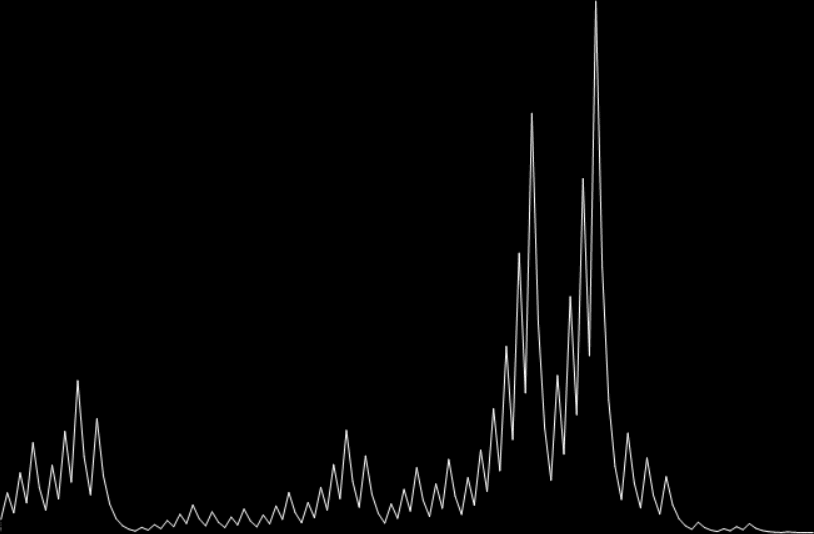
Graph for hail(27) = 111 (mx=9232)

27 takes 111 steps to reach 1. And the 111 made me think of another question. If the function hail(n) returns the number of steps required for n to reach 1, then hail(27) = 111. But what about hail(n) = 666? That is, what is the first number that requires 666 steps to reach 1? I say “first number”, because one very big number is guaranteed to take 666 steps:

666 = hail(306,180,206,916,083,902,309,240,650,087,602,475,282,639,486,413,866,622,
577,088,471,913,520,022,894,784,390,350,900,738,050,555,138,105,234,536,857,820,245,
071,373,614,031,482,942,161,565,170,086,143,298,589,738,273,508,330,367,307,539,078,
392,896,587,187,265,470,464)

Put another way, 666 = hail(2^666), because for any power of 2, hail(2^p) = p. But is there a smaller number, which I’ll call satan, for which hail(satan) = 666? Here’s a tantalizing taster of the task:

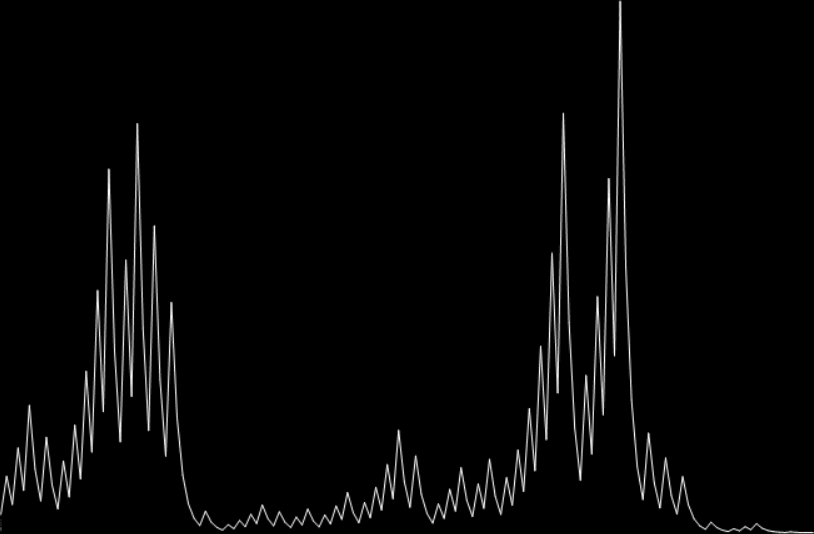
hail(27) = 111 (mx=9232)
hail(30262) = 222 (mx=2484916)
hail(164521) = 333 (mx=21933016)
hail(886953) = 444 (mx=52483285312)
hail(5143151) = 555 (mx=125218704148)
hail(satan) = 666 (mx=?)

But what is satan? Before I answer, here are some more graphs for interesting hail(n):

hail(231) = 127 (mx=9232)

hail(327) = 143 (mx=9232)

hail(703) = 170 (mx=250504)

hail(871) = 178 (mx=190996)

hail(2223) = 182 (mx=250504)

hail(3711) = 237 (mx=481624)

hail(35655) = 323 (mx=41163712)

hail(142587) = 374 (mx=593279152)

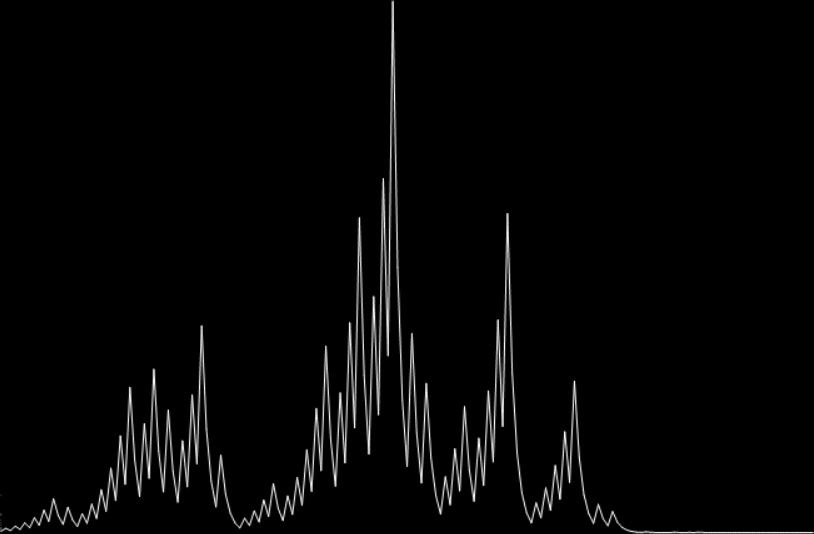
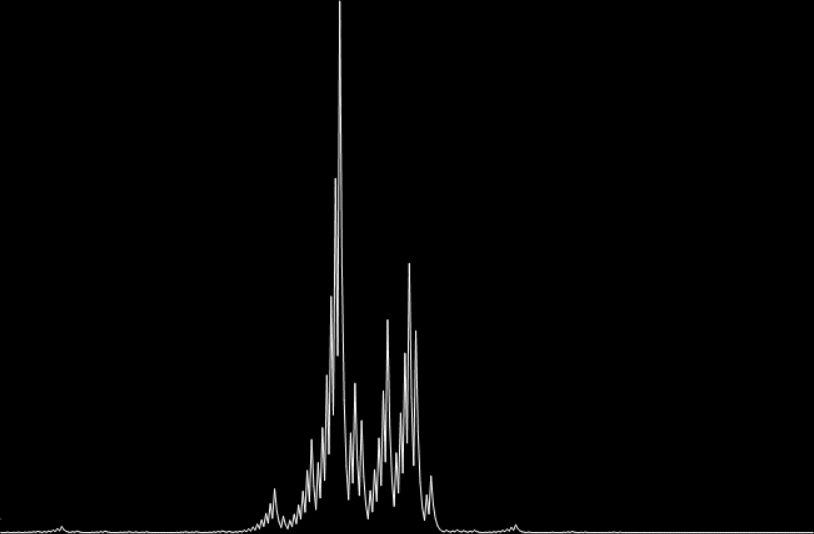
Now I’ll answer the question. If satan = 26597116, then hail(satan) = 666:

hail(26597116) = 666 (mx=15208728208)

Therefore:

hail(satan)! =
1,010,632,056,840,781,493,390,822,708,129,876,451,757,582,398,324,145,411,
340,420,807,357,413,802,103,697,022,989,202,806,801,491,012,040,989,802,
203,557,527,039,339,704,057,130,729,302,834,542,423,840,165,856,428,740,
661,530,297,972,410,682,828,699,397,176,884,342,513,509,493,787,480,774,
903,493,389,255,262,878,341,761,883,261,899,426,484,944,657,161,693,131,
380,311,117,619,573,051,526,423,320,389,641,805,410,816,067,607,893,067,
483,259,816,815,364,609,828,668,662,748,110,385,603,657,973,284,604,842,
078,094,141,556,427,708,745,345,100,598,829,488,472,505,949,071,967,727,
270,911,965,060,885,209,294,340,665,506,480,226,426,083,357,901,503,097,
781,140,832,497,013,738,079,112,777,615,719,116,203,317,542,199,999,489,
227,144,752,667,085,796,752,482,688,850,461,263,732,284,539,176,142,365,
823,973,696,764,537,603,278,769,322,286,708,855,475,069,835,681,643,710,
846,140,569,769,330,065,775,414,413,083,501,043,659,572,299,454,446,517,
242,824,002,140,555,140,464,296,291,001,901,438,414,675,730,552,964,914,
569,269,734,038,500,764,140,551,143,642,836,128,613,304,734,147,348,086,
095,123,859,660,926,788,460,671,181,469,216,252,213,374,650,499,557,831,
741,950,594,827,147,225,699,896,414,088,694,251,261,045,196,672,567,495,
532,228,826,719,381,606,116,974,003,112,642,111,561,332,573,503,212,960,
729,711,781,993,903,877,416,394,381,718,464,765,527,575,014,252,129,040,
283,236,963,922,624,344,456,975,024,058,167,368,431,809,068,544,577,258,
472,983,979,437,818,072,648,213,608,650,098,749,369,761,056,961,203,791,
265,363,665,664,696,802,245,199,962,040,041,544,438,210,327,210,476,982,
203,348,458,596,093,079,296,569,561,267,409,473,914,124,132,102,055,811,
493,736,199,668,788,534,872,321,705,360,511,305,248,710,796,441,479,213,
354,542,583,576,076,596,250,213,454,667,968,837,996,023,273,163,069,094,
700,429,467,106,663,925,419,581,193,136,339,860,545,658,673,623,955,231,
932,399,404,809,404,108,767,232,000,000,000,000,000,000,000,000,000,000,
000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,
000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,
000,000,000,000,000,000,000,000,000 = 666!

Here’s a question I haven’t answered: if satanic numbers are those n satisfying hail(n) = 666, how many satanic numbers are there? We’ve already seen two of them: 666 = hail(2^666) = hail(26597116). But how many more are there? Not infinitely many, because for n > 2^666, hail(n) > 666. In fact, after satan = 26597116, the next three satanic numbers arrive very quickly:

hail(satan+0) = 666 = hail(26597116)
hail(satan+1) = 666 = hail(26597117)
hail(satan+2) = 666 = hail(26597118)
hail(satan+3) = 666 = hail(26597119)

hail(satan-1) = 180 = hail(26597115)
hail(satan+4) = 180 = hail(26597120)

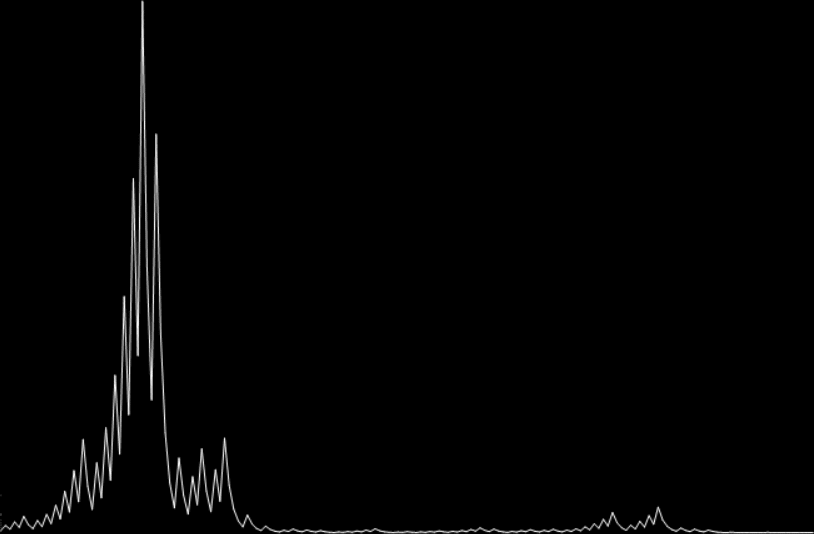
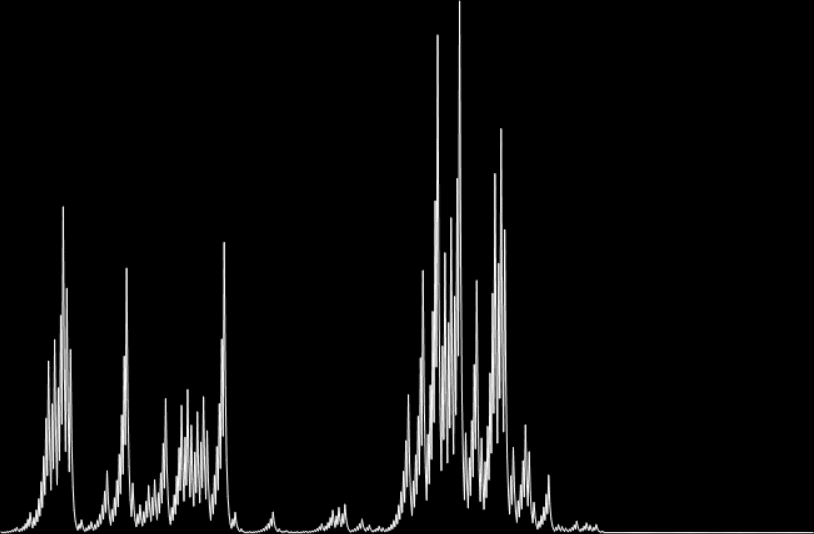
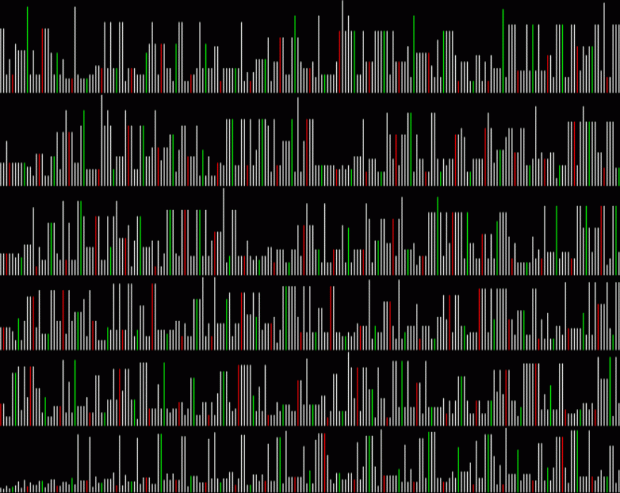
So there are four consecutive satanic numbers. But it isn’t unusual for a run of consecutive numbers to have the same hail(). Here’s a graph of the values of hail(n) for n = 1,2,3… (running left-to-right, down-up, with 1,2,3… in the lower lefthand corner). When n is divisible by 10, hail(n) is represented in red; when n is odd and divisible by 5, hail(n) is green. Note how many runs of identical hail(n) there are:

Graph for hail(n)

Here are successive records for runs of identical hail(n):

hail(12..13) = 9 (run=2)
hail(28..30) = 18 (run=3)
hail(98..102) = 25 (r=5)
hail(386..391) = 120 (r=6)
hail(943..949) = 36 (r=7)
hail(1494..1501) = 47 (r=8)
hail(1680..1688) = 42 (r=9)
hail(2987..3000) = 48 (r=14)
hail(7083..7099) = 57 (r=17)
hail(57346..57370) = 78 (r=25)
hail(252548..252574) = 181 (r=27)
hail(331778..331806) = 91 (r=29)
hail(524289..524318) = 102 (r=30)
hail(596310..596349) = 97 (r=40)

Finally, here’s Poland’s finest putting the function of 26597116 to music:

“Hail Satan!” by Dopelord

Elsewhere Other-Accessible…

• Dopelord at Bandcamp