Abstract: The game of chess is the most widely-studied domain in the history of artificial intelligence. The strongest programs are based on a combination of sophisticated search techniques, domain-specific adaptations, and handcrafted evaluation functions that have been refined by human experts over several decades. In contrast, the AlphaGo Zero program recently achieved superhuman performance in the game of Go, by tabula rasa reinforcement learning from games of self-play. In this paper, we generalise this approach into a single AlphaZero algorithm that can achieve, tabula rasa, superhuman performance in many challenging domains. Starting from random play, and given no domain knowledge except the game rules, AlphaZero achieved within 24 hours a superhuman level of play in the games of chess and shogi (Japanese chess) as well as Go, and convincingly defeated a world-champion program in each case. — “Mastering Chess and Shogi by Self-Play with a General Reinforcement Learning Algorithm”, 5/XII/2017.
Tag Archives: algorithms
Self-Raising Power
The square root of 2 is the number that, raised to the power of 2, equals 2. That is, if r^2 = r * r = 2, then r = √2. The cube root of 2 is the number that, raised to the power of 3, equals 2. That is, if r^3 = r * r * r = 2, then r = [3]√2.
But what do you call the number that, raised to the power of itself, equals 2? I suggest “the auto-root of 2”. Here, if r^r = 2, then r = [r]√2. I don’t know a quick way to calculate the auto-root, but you can adapt a well-known algorithm for approximating the square root of a number. The square-root algorithm looks like this:
n = 2
r = 1
for c = 1 to 20
r = (r + n/r) / 2
next c
print rr = 1.414213562…
Note the fourth line of the algorithm: r = (r + n/r) / 2. When r is an over-estimate of √2, then 2/r will be an under-estimate (and vice versa). (r + 2/r) / 2 splits the difference and refines the estimate. Using the lines above as the model, the auto-root algorithm looks like this:
n = 2
r = 1
for c = 1 to 20
r = (r + [r]√n) / 2[*]
next c
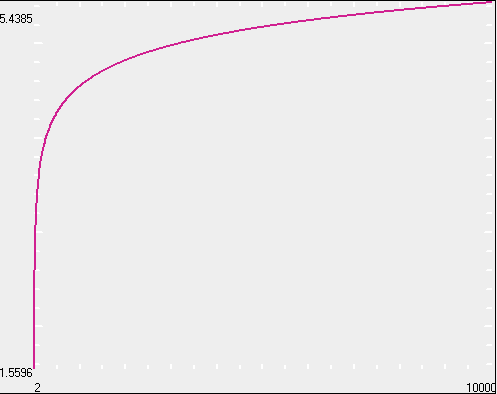
print rr = 1.559610469…
*This is equivalent to r = (r + n^(1/r)) / 2
Here are the first 100 digits of [r]√2 = r in base 10:
1, 5, 5, 9, 6, 1, 0, 4, 6, 9, 4, 6, 2, 3, 6, 9, 3, 4, 9, 9, 7, 0, 3, 8, 8, 7, 6, 8, 7, 6, 5, 0, 0, 2, 9, 9, 3, 2, 8, 4, 8, 8, 3, 5, 1, 1, 8, 4, 3, 0, 9, 1, 4, 2, 4, 7, 1, 9, 5, 9, 4, 5, 6, 9, 4, 1, 3, 9, 7, 3, 0, 3, 4, 5, 4, 9, 5, 9, 0, 5, 8, 7, 1, 0, 5, 4, 1, 3, 4, 4, 4, 6, 9, 1, 2, 8, 3, 9, 7, 3…
And here is [r]√n = r for n = 2..20:
autopower(2) = 1.5596104694623693499703887…
autopower(3) = 1.8254550229248300400414692…
autopower(4) = 2
autopower(5) = 2.1293724827601566963803119…
autopower(6) = 2.2318286244090093673920215…
autopower(7) = 2.3164549587856123013255030…
autopower(8) = 2.3884234844993385564187215…
autopower(9) = 2.4509539280155796306228059…
autopower(10) = 2.5061841455887692562929409…
autopower(11) = 2.5556046121008206152514542…
autopower(12) = 2.6002950000539155877172082…
autopower(13) = 2.6410619164843958084118390…
autopower(14) = 2.6785234858912995813011990…
autopower(15) = 2.7131636040042392095764012…
autopower(16) = 2.7453680235674634847098492…
autopower(17) = 2.7754491049442334313328329…
autopower(18) = 2.8036632456580215496843618…
autopower(19) = 2.8302234384970308956026277…
autopower(20) = 2.8553085030012414128332189…
I assume that the auto-root is always an irrational number, except when n is a perfect power of suitable form, i.e. n = p^p for some integer p. For example, autoroot(4) = 2, because 2^2 = 4, autoroot(27) = 3, because 3^3 = 27, and so on.
And here is the graph of autoroot(n) for n = 2..10000:
Summer-Climb Views
Simple things can sometimes baffle advanced minds. If you take a number, reverse its digits, add the result to the original number, then repeat all that, will you eventually get a palindrome? (I.e., a number, like 343 or 27172, that reads the same in both directions.) Many numbers do seem to produce palindromes sooner or later. Here are 195 and 197:
195 + 591 = 786 + 687 = 1473 + 3741 = 5214 + 4125 = 9339 (4 steps)
197 + 791 = 988 + 889 = 1877 + 7781 = 9658 + 8569 = 18227 + 72281 = 90508 + 80509 = 171017 + 710171 = 881188 (7 steps)
But what about 196? Well, it starts like this:
196 + 691 = 887 + 788 = 1675 + 5761 = 7436 + 6347 = 13783 + 38731 = 52514 + 41525 = 94039 + 93049 = 187088 + 880781 = 1067869 + 9687601 = 10755470 + 7455701 = 18211171 + 17111281 = 35322452 + 25422353 = 60744805 + 50844706 = 111589511 + 115985111 = 227574622 + 226475722 = 454050344 + 443050454 = 897100798 + 897001798 = 1794102596 + 6952014971 = 8746117567 + 7657116478 = 16403234045 + 54043230461 = 70446464506 + 60546464407 = 130992928913 + 319829299031 = 450822227944 + 449722228054 = 900544455998…
And so far, after literally years of computing by mathematicians, it hasn’t produced a palindrome. It seems very unlikely it ever will, but no-one can prove this and say that 196 is, in base 10, a Lychrel number, or a number that never produces a palindrome. In other words, a simple thing has baffled advanced minds.
I don’t know whether it can baffle advanced minds, but here’s another simple mathematical technique: sum all the digits of a number, then add the result to the original number and repeat. How long before a palindrome appears in this case? Sum it and see:
10 + 1 = 11
12 + 3 = 15 + 6 = 21 + 3 = 24 + 6 = 30 + 3 = 33 (5 steps)
13 + 4 = 17 + 8 = 25 + 7 = 32 + 5 = 37 + 10 = 47 + 11 = 58 + 13 = 71 + 8 = 79 + 16 = 95 + 14 = 109 + 10 = 119 + 11 = 130 + 4 = 134 + 8 = 142 + 7 = 149 + 14 = 163 + 10 = 173 + 11 = 184 + 13 = 197 + 17 = 214 + 7 = 221 + 5 = 226 + 10 = 236 + 11 = 247 + 13 = 260 + 8 = 268 + 16 = 284 + 14 = 298 + 19 = 317 + 11 = 328 + 13 = 341 + 8 = 349 + 16 = 365 + 14 = 379 + 19 = 398 + 20 = 418 + 13 = 431 + 8 = 439 + 16 = 455 + 14 = 469 + 19 = 488 + 20 = 508 + 13 = 521 + 8 = 529 + 16 = 545 (45 steps)
14 + 5 = 19 + 10 = 29 + 11 = 40 + 4 = 44 (4 steps)
15 + 6 = 21 + 3 = 24 + 6 = 30 + 3 = 33 (4 steps)
16 + 7 = 23 + 5 = 28 + 10 = 38 + 11 = 49 + 13 = 62 + 8 = 70 + 7 = 77 (7 steps)
17 + 8 = 25 + 7 = 32 + 5 = 37 + 10 = 47 + 11 = 58 + 13 = 71 + 8 = 79 + 16 = 95 + 14 = 109 + 10 = 119 + 11 = 130 + 4 = 134 + 8 = 142 + 7 = 149 + 14 = 163 + 10 = 173 + 11 = 184 + 13 = 197 + 17 = 214 + 7 = 221 + 5 = 226 + 10 = 236 + 11 = 247 + 13 = 260 + 8 = 268 + 16 = 284 + 14 = 298 + 19 = 317 + 11 = 328 + 13 = 341 + 8 = 349 + 16 = 365 + 14 = 379 + 19 = 398 + 20 = 418 + 13 = 431 + 8 = 439 + 16 = 455 + 14 = 469 + 19 = 488 + 20 = 508 + 13 = 521 + 8 = 529 + 16 = 545 (44 steps)
18 + 9 = 27 + 9 = 36 + 9 = 45 + 9 = 54 + 9 = 63 + 9 = 72 + 9 = 81 + 9 = 90 + 9 = 99 (9 steps)
19 + 10 = 29 + 11 = 40 + 4 = 44 (3 steps)
20 + 2 = 22
I haven’t looked very thoroughly at this technique, so I don’t know whether it throws up a seemingly unpalindromizable number. If it does, I don’t have an advanced mind, so I won’t be able to prove that it is unpalindromizable. But an adaptation of the technique produces something interesting when it is represented on a graph. This time, if s > 9, where s = digit-sum(n), let s = digit-sum(s) until s <= 9 (i.e, s < 10, the base). I call this the condensed digit-sum:
140 + 5 = 145 + 1 = 146 + 2 = 148 + 4 = 152 + 8 = 160 + 7 = 167 + 5 = 172 + 1 = 173 + 2 = 175 + 4 = 179 + 8 = 187 + 7 = 194 + 5 = 199 + 1 = 200 + 2 = 202 (15 steps)
Here, for comparison, is the sequence for 140 using uncondensed digit-sums:
140 + 5 = 145 + 10 = 155 + 11 = 166 + 13 = 179 + 17 = 196 + 16 = 212 (6 steps)
When all the numbers (including palindromes) created using condensed digit-sums are shown on a graph, they create an interesting pattern in base 10 (the x-axis represents n, the y-axis represents n, n1 = n + digit-sum(n), n2 = n1 + digit-sum(n1), etc):
(Please open images in a new window if they fail to animate.)
And here, for comparison, are the patterns created by uncondensed digit-sums in base 2 to 10:
Overlord In Terms of Core Issues Around Maximal Engagement with Key Notions of the Über-Feral 