This is the surpassingly special Stern-Brocot sequence:

0, 1, 1, 2, 1, 3, 2, 3, 1, 4, 3, 5, 2, 5, 3, 4, 1, 5, 4, 7, 3, 8, 5, 7, 2, 7, 5, 8, 3, 7, 4, 5, 1, 6, 5, 9, 4, 11, 7, 10, 3, 11, 8, 13, 5, 12, 7, 9, 2, 9, 7, 12, 5, 13, 8, 11, 3, 10, 7, 11, 4, 9, 5, 6, 1, 7, 6, 11, 5, 14, 9, 13, 4, 15, 11, 18, 7, 17, 10, 13, 3, 14, 11, 19, 8, 21, 13, 18, 5, 17, 12, 19, … (A002487 at the Online Encyclopedia of Integer Sequences)

---

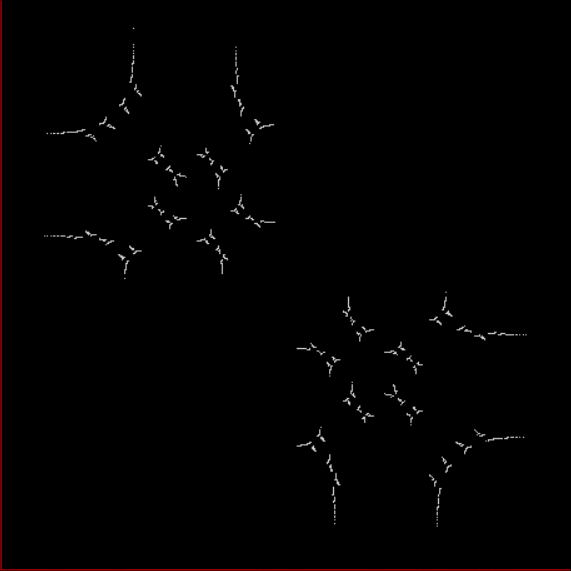
And why is the sequence special? Because if you take successive pairs of the apparently arbitrarily varying numbers, you get every rational fraction in its simplest form exactly once. So 1/2, 2/3, 6/11 and 502/787 appear once and then never again. And so do 2/1, 3/2, 11/6 and 787/502. Et cetera, ad infinitum. If you map the Stern-Brocot sequence against the related Calkin-Wilk sequence, which has the same “all-simplest-fractions-exactly-once” properties, you can create this fractal, which I call a limestone fractal or gryke fractal:

Gryke fractal by mapping Stern-Brocot sequence against Calkin-Wilf sequence

---

The graph is what I call a Fract-L, because the lines for the x,y coordinates create an L. Each coordinate runs from 0 to 1, with the x set by the fraction from the Stern-Brocot sequence and the y set by the fraction from the Calkin-Wilf sequence (if a > b in a/b, use the conversion 1/(a/b) = b/a). But you can also find interesting patterns by mapping the Stern-Brocot sequence against itself. That is, you use two Stern-Brocot sequences that start in different places. Now, there are complicated ways to create the Stern-Brocot sequence using mathematical trees and sequential algorithms and so on. But there’s also an astonishingly simple way, a formula created by the Israeli mathematician Moshe Newman. If (a,b) is one pair of successive numbers in the sequence, the next pair (a,b) is found like this:

c = b
b = (2 * int(a/b) + 1) * b – a
a = c

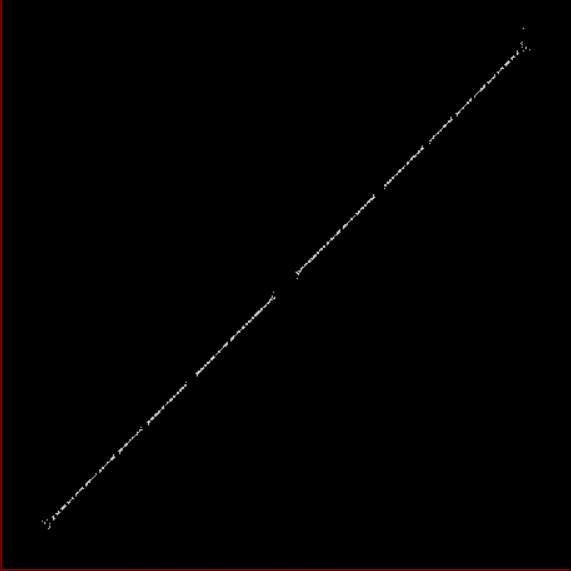
This means that you can seed a Stern-Brocot sequence with any (correctly simplified) a/b and it will continue in the right way. If the two SB-sequences for x and y are both seeded with (0,1), you get this 45° line, because each successive a/b for (x,y) is identical:

Stern-Brocot pairs seeded with x ← (0,1) and y ← (0,1)

---

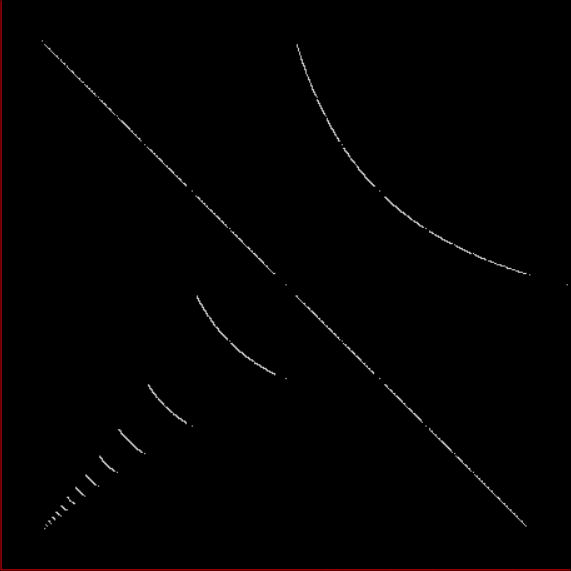
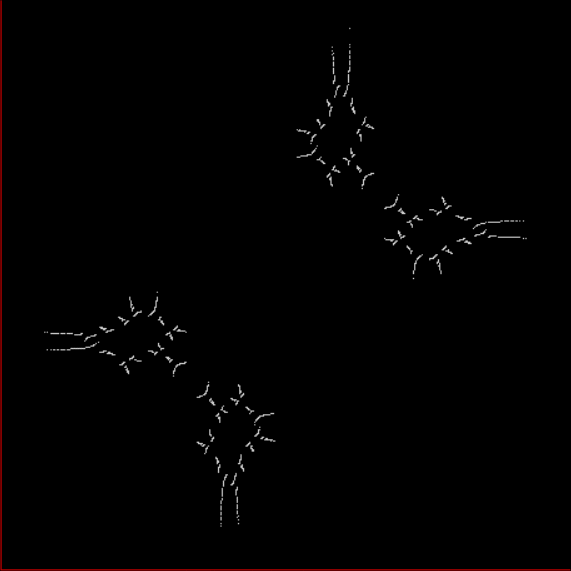
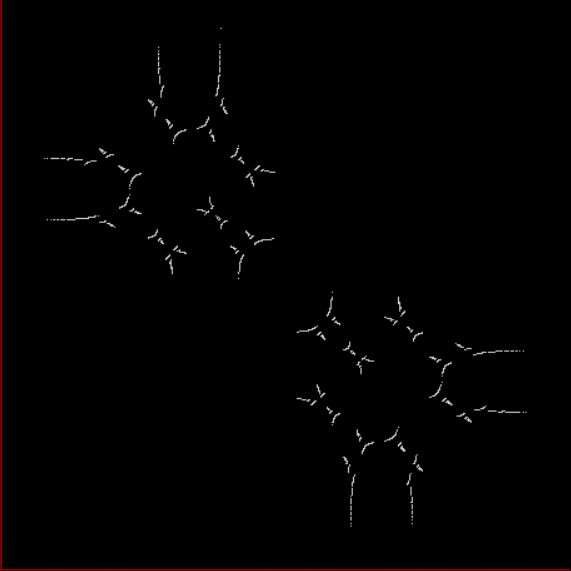
The further you extend the sequences, the less broken the 45° line will appear, because the points determined by a/b for x and y will get closer and closer together (but the line will never be solid, because any two rationals are separated by an infinity of irrationals). Now try offsetting the SB-sequences for x,y by using different seeds. Different fractal patterns appear, which all appear to be subsets (or fractions) of the limestone fractal above (see animated gif below):

Stern-Brocot pairs seeded with x ← (0,1) and y ← (1,1)

---

x ← (0,1) and y ← (1,2)

---

x ← (0,1) and y ← (1,3)

---

x ← (0,1) and y ← (2,3)

---

x ← (0,1) and y ← (3,4)

---

x ← (0,1) and y ← (6,7)

---

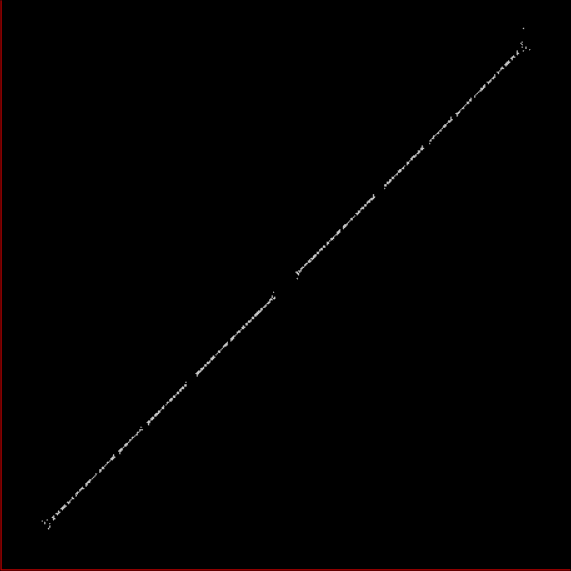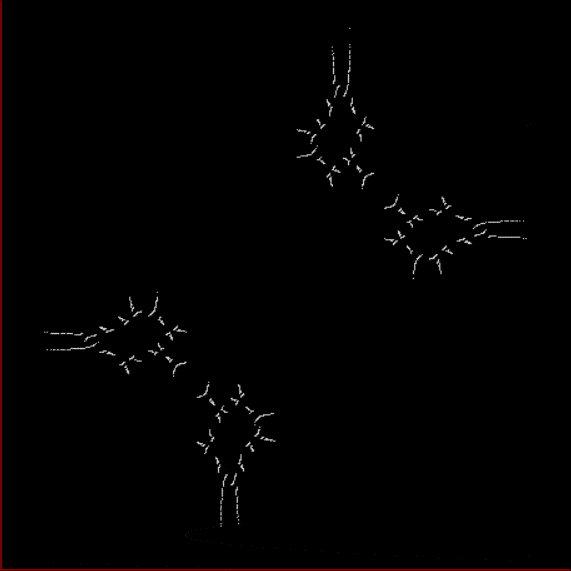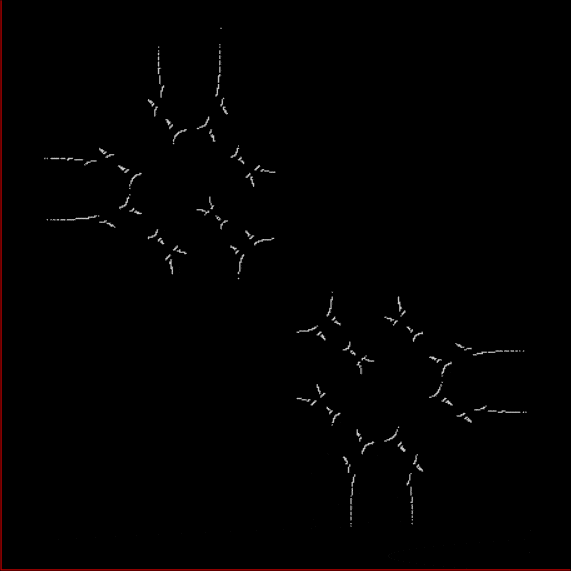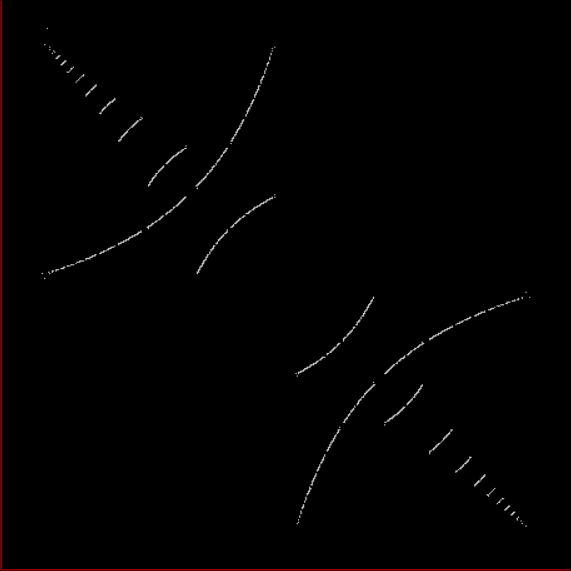
x ← (1,2) and y ← (1,9)

---

x ← (1,4) and y ← (1,6)

---

x ← (1,7) and y ← (1,8)

---

x ← (2,3) and y ← (4,5) — apparently identical to x ← (1,4) and y ← (1,6) above

---

x ← (26,25) and y ← (1,10)

---

Gryke fractal compared with Stern-Brocot-pair patterns (animated at ezGif)

---

And here’s what happens when the seed-fractions for x run from 1/3 to 12/13, while the seed-fraction for y is held constant at 1/23:

x ← (1,13) and y ← (1,23)

---

x ← (2,13) and y ← (1,23)

---

x ← (3,13) and y ← (1,23)

---

x ← (4,13) and y ← (1,23)

---

x ← (5,13) and y ← (1,23)

---

x ← (6,13) and y ← (1,23)

---

x ← (7,13) and y ← (1,23)

---

x ← (8,13) and y ← (1,23)

---

x ← (9,13) and y ← (1,23)

---

x ← (10,13) and y ← (1,23)

---

x ← (11,13) and y ← (1,23)

---

x ← (12,13) and y ← (1,23)

---

Animated gif for x ← (n,13) and y ← (1,23) (animated at ezGif)

---

Previously Pre-Posted

• I Like Gryke — a first look at the limestone fractal
• Lime Time — more on the fractal