Tag Archives: perfect numbers

Abounding in Abundants

by in Arithmetic, Integer Sequences, Mathematics, Prime numbers and tagged , , , , , , , , , , , , , , , , | Leave a comment

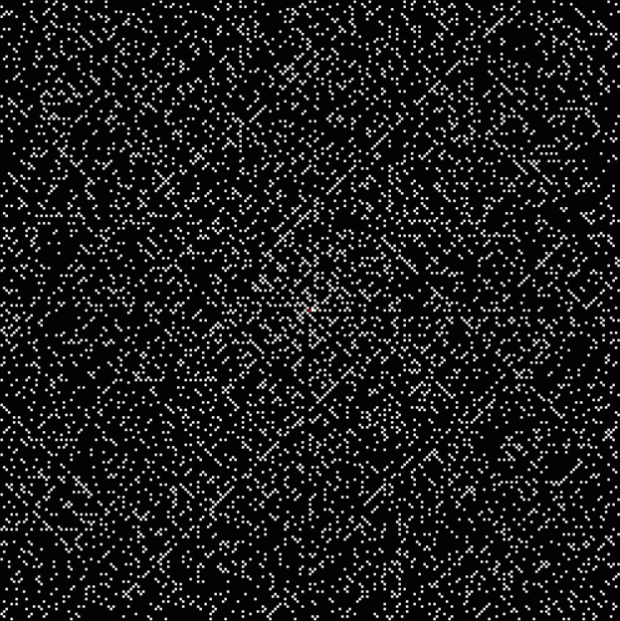
This is the famous Ulam spiral, invented by the Jewish mathematician Stanisław Ulam (pronounced OO-lam) to represent prime numbers on a square grid:

The Ulam spiral of prime numbers

The red square represents 1, with 2 as the white block immediately to its right and 3 immediately above 2. Then 5 is the white block one space to the left of 3 and 7 the white block one space below 5. Then 11 is the white block right beside 2 and 13 the white block one space above 11. And so on. The primes aren’t regularly spaced on the spiral but patterns are nevertheless appearing. Here’s the Ulam spiral at higher resolutions:

The Ulam spiral x2

The Ulam spiral x4

The primes are neither regular nor random in their distribution on the spiral. They stand tantalizingly betwixt and between. So the numbers represented on this Ulam-like spiral, which looks like an aerial view of a city designed by architects who occasionally get drunk:

Ulam-like spiral of abundant numbers

The distribution of abundant numbers is much more regular than the primes, but is far from wholly predictable. And what are abundant numbers? They’re numbers n such that sum(divisors(n)-n) > n. In other words, when you add the divisors of n less than n, the sum is greater than n. The first abundant number is 12:

12 is divisible by 1, 2, 3, 4, 6 → 1 + 2 + 3 + 4 + 6 = 16 > 12

The abundant numbers go like this:

12, 18, 20, 24, 30, 36, 40, 42, 48, 54, 56, 60, 66, 70, 72, 78, 80, 84, 88, 90, 96, 100, 102, 104, 108, 112, 114, 120, 126, 132, 138, 140, 144, 150, 156, 160, 162, 168, 174, 176, 180, 186, 192, 196, 198, 200, 204, 208, 210, 216, 220, 222, 224, 228, 234, 240, 246, 252, 258, 260, 264, 270… — A005101 at the Online Encyclopedia of Integer Sequences

Are all abundant numbers even? No, but the first odd abundant number takes a long time to arrive: it’s 45045. The abundance of 45045 was first discovered by the French mathematician Charles de Bovelles or Carolus Bovillus (c. 1475-1566), according to David Wells in his wonderful Penguin Dictionary of Curious and Interesting Numbers (1986):

45045 = 3^2 * 5 * 7 * 11 * 13 → 1 + 3 + 5 + 7 + 9 + 11 + 13 + 15 + 21 + 33 + 35 + 39 + 45 + 55 + 63 + 65 + 77 + 91 + 99 + 105 + 117 + 143 + 165 + 195 + 231 + 273 + 315 + 385 + 429 + 455 + 495 + 585 + 693 + 715 + 819 + 1001 + 1155 + 1287 + 1365 + 2145 + 3003 + 3465 + 4095 + 5005 + 6435 + 9009 + 15015 = 59787 > 45045

Here’s the spiral of abundant numbers at higher resolutions:

Abundant numbers x2

Abundant numbers x4

Negating the spiral of the abundant numbers — almost — is the spiral of the deficient numbers, where sum(divisors(n)-n) < n. Like most odd numbers, 15 is deficient:

15 = 3 * 5 → 1 + 3 + 5 = 9 < 15

Here’s the spiral of deficient numbers at various resolutions:

Deficient numbers on Ulam-like spiral

Deficient numbers x2

Deficient numbers x4

The spiral of deficient numbers doesn’t quite negate (reverse the colors of) the spiral of abundant numbers because of the very rare perfect numbers, where sum(divisors(n)-n) = n. That is, their factor-sums are exactly equal to themselves:

• 6 = 2 * 3 → 1 + 2 + 3 = 6
• 28 = 2^2 * 7 → 1 + 2 + 4 + 7 + 14 = 28
• 496 = 2^4 * 31 → 1 + 2 + 4 + 8 + 16 + 31 + 62 + 124 + 248 = 496

Now let’s try numbers n such than sum(divisors(n)) mod 2 = 1 (“n mod 2″ gives the remainder when n is divided by 2, i.e. n mod 2 is either 0 or 1). For example:

• 4 = 2^2 → 1 + 2 + 4 = 7 → 7 mod 2 = 1
• 18 = 2 * 3^2 → 1 + 2 + 3 + 6 + 9 + 18 = 39 → 39 mod 2 = 1
• 72 = 2^3 * 3^2 → 1 + 2 + 3 + 4 + 6 + 8 + 9 + 12 + 18 + 24 + 36 + 72 = 195 → 195 mod 2 = 1

Here are spirals for these numbers:

Ulam-like spiral for n such than sum(divisors(n)) mod 2 = 1

sum(divisors(n)) mod 2 = 1 x2

sum(divisors(n)) mod 2 = 1 x4

sum(divisors(n)) mod 2 = 1 x8

sum(divisors(n)) mod 2 = 1 x16

Factory Records

by in Base Behavior, Mathematics, Palindromic numbers, Prime numbers and tagged , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , | Leave a comment

The factors of n are those numbers that divide n without remainder. So the factors of 6 are 1, 2, 3 and 6. If the function s(n) is defined as “the sum of the factors of n, excluding n”, then s(6) = 1 + 2 + 3 = 6. This makes 6 a perfect number: its factors re-create it. 28 is another perfect number. The factors of 28 are 1, 2, 4, 7, 14 and 28, so s(28) = 1 + 2 + 4 + 7 + 14 = 28. Other perfect numbers are 496 and 8128. And they’re perfect in any base.

Amicable numbers are amicable in any base too. The factors of an amicable number sum to a second number whose factors sum to the first number. So s(220) = 284, s(284) = 220. That pair may have been known to Pythagoras (c.570-c.495 BC), but s(1184) = 1210, s(1210) = 1184 was discovered by an Italian schoolboy called Nicolò Paganini in 1866. There are also sociable chains, in which s(n), s(s(n)), s(s(s(n))) create a chain of numbers that leads back to n, like this:

12496 → 14288 → 15472 → 14536 → 14264 → 12496 (c=5)

Or this:

14316 → 19116 → 31704 → 47616 → 83328 → 177792 → 295488 → 629072 → 589786 → 294896 → 358336 → 418904 → 366556 → 274924 → 275444 → 243760 → 376736 → 381028 → 285778 → 152990 → 122410 → 97946 → 48976 → 45946 → 22976 → 22744 → 19916 → 17716 → 14316 (c=28)

Those sociable chains were discovered (and christened) in 1918 by the Belgian mathematician Paul Poulet (1887-1946). Other factor-sum patterns are dependant on the base they’re expressed in. For example, s(333) = 161. So both n and s(n) are palindromes in base-10. Here are more examples — the numbers in brackets are the prime factors of n and s(n):

333 (3^2, 37) → 161 (7, 23)
646 (2, 17, 19) → 434 (2, 7, 31)
656 (2^4, 41) → 646 (2, 17, 19)
979 (11, 89) → 101 (prime)
1001 (7, 11, 13) → 343 (7^3)
3553 (11, 17, 19) → 767 (13, 59)
10801 (7, 1543) → 1551 (3, 11, 47)
11111 (41, 271) → 313 (prime)
18581 (17, 1093) → 1111 (11, 101)
31713 (3, 11, 31^2) → 15951 (3, 13, 409)
34943 (83, 421) → 505 (5, 101)
48484 (2^2, 17, 23, 31) → 48284 (2^2, 12071)
57375 (3^3, 5^3, 17) → 54945 (3^3, 5, 11, 37)
95259 (3, 113, 281) → 33333 (3, 41, 271)
99099 (3^2, 7, 11^2, 13) → 94549 (7, 13, 1039)
158851 (7, 11, 2063) → 39293 (prime)
262262 (2, 7, 11, 13, 131) → 269962 (2, 7, 11, 1753)
569965 (5, 11, 43, 241) → 196691 (11, 17881)
1173711 (3, 7, 11, 5081) → 777777 (3, 7^2, 11, 13, 37)

Note how s(656) = 646 and s(646) = 434. There’s an even longer sequence in base-495:

33 → 55 → 77 → 99 → [17][17] → [19][19] → [21][21] → [43][43] → [45][45] → [111][111] → [193][193] → [195][195] → [477][477] (b=495) (c=13)
1488 (2^4, 3, 31) → 2480 (2^4, 5, 31) → 3472 (2^4, 7, 31) → 4464 (2^4, 3^2, 31) → 8432 (2^4, 17, 31) → 9424 (2^4, 19, 31) → 10416 (2^4, 3, 7, 31) → 21328 (2^4, 31, 43) → 22320 (2^4, 3^2, 5, 31) → 55056 (2^4, 3, 31, 37) → 95728 (2^4, 31, 193) → 96720 (2^4, 3, 5, 13, 31) → 236592 (2^4, 3^2, 31, 53)

I also tried looking for n whose s(n) mirrors n. But they’re hard to find in base-10. The first example is this:

498906 (2, 3^3, 9239) → 609894 (2, 3^2, 31, 1093)

498906 mirrors 609894, because the digits of each run in reverse to the digits of the other. Base-9 does better for mirror-sums, clocking up four in the same range of integers:

42 → 24 (base=9)
38 (2, 19) → 22 (2, 11)
402 → 204 (base=9)
326 (2, 163) → 166 (2, 83)
4002 → 2004 (base=9)
2918 (2, 1459) → 1462 (2, 17, 43)
5544 → 4455 (base=9)
4090 (2, 5, 409) → 3290 (2, 5, 7, 47)

Base-11 does better still, clocking up eight in the same range:

42 → 24 (base=11)
46 (2, 23) → 26 (2, 13)
2927 → 7292 (base=11)
3780 (2^2, 3^3, 5, 7) → 9660 (2^2, 3, 5, 7, 23)
4002 → 2004 (base=11)
5326 (2, 2663) → 2666 (2, 31, 43)
13772 → 27731 (base=11)
19560 (2^3, 3, 5, 163) → 39480 (2^3, 3, 5, 7, 47)
4[10]7[10]9 → 9[10]7[10]4 (base=11)
72840 (2^3, 3, 5, 607) → 146040 (2^3, 3, 5, 1217)
6929[10] → [10]9296 (base=11)
100176 (2^4, 3, 2087) → 158736 (2^4, 3, 3307)
171623 → 326171 (base=11)
265620 (2^2, 3, 5, 19, 233) → 520620 (2^2, 3, 5, 8677)
263702 → 207362 (base=11)
414790 (2, 5, 41479) → 331850 (2, 5^2, 6637)

Note that 42 mirrors its factor-sum in both base-9 and base-11. But s(42) = 24 in infinitely many bases, because when 42 = 2 x prime, s(42) = 1 + 2 + prime. So (prime-1) / 2 will give the base in which 24 = s(42). For example, 2 x 11 = 22 and 22 = 42 in base (11-1) / 2 or base-5. So s(42) = 1 + 2 + 11 = 14 = 2 x 5 + 4 = 24[b=5]. There are infinitely many primes, so infinitely many bases in which s(42) = 24.

Base-10 does better for mirror-sums when s(n) is re-defined to include n itself. So s(69) = 1 + 3 + 23 + 69 = 96. Here are the first examples of all-factor mirror-sums in base-10:

69 (3, 23) → 96 (2^5, 3)
276 (2^2, 3, 23) → 672 (2^5, 3, 7)
639 (3^2, 71) → 936 (2^3, 3^2, 13)
2556 (2^2, 3^2, 71) → 6552 (2^3, 3^2, 7, 13)

In the same range, base-9 now produces one mirror-sum, 13 → 31 = 12 (2^2, 3) → 28 (2^2, 7). Base-11 produces no mirror-sums in the same range. Base behaviour is eccentric, but that’s what makes it interesting.