Tag Archives: perimeters

Punctuated Pairimeters

by in Arithmetic, Circles, Geometry, Mathematics and tagged , , , , | Leave a comment

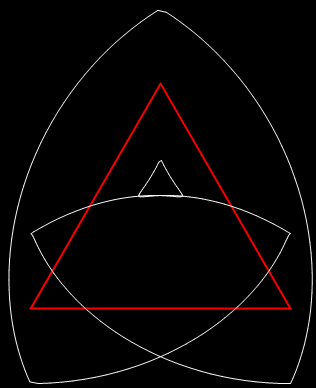
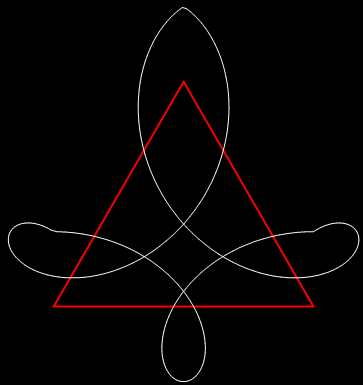
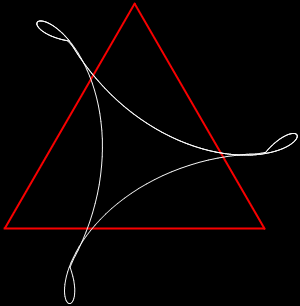
Imagine using the digits of n in two different bases to generate two fractions, a/b and c/d, where a/b < 1 and c/d < 1 (see Appendix for a sample program). Now use the fractions to find a pair of points on the perimeter of a circle, (x1, y1) and (x2, y2), then calculate and mark the midpoint of (x1, y1) and (x2, y2). If the bases have a prime factor in common, pretty patterns will appear from this punctuated pairimetry:

b1 = 2; b2 = 6

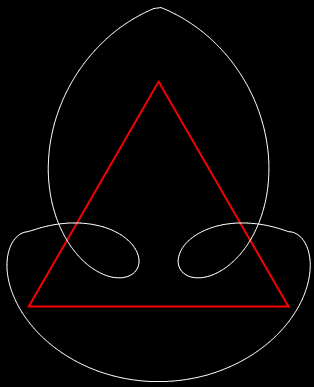
b1 = 2; b2 = 10

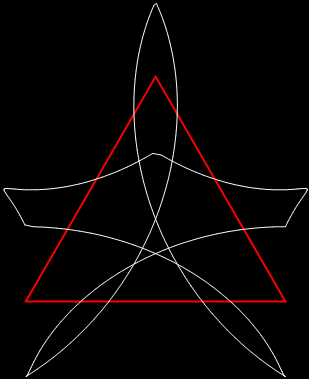
b1 = 2; b2 = 14

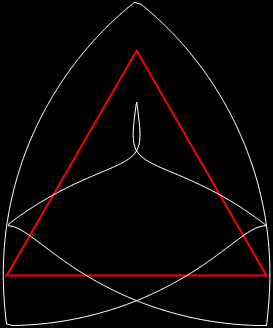
b1 = 4; b2 = 10

b1 = 4; b2 = 20

b1 = 4; b2 = 28

b1 = 6; b2 = 42

b1 = 12; b2 = 39

b1 = 24; b2 = 28

b1 = 28; b2 = 40

b1 = 32; b2 = 36

b1 = 42; b2 = 78

Appendix: Sample Program for Pairimetry

GetXY(xyi)=

fr = 0
recip = 1
bs = base[xyi]
for gi = 1 to di[xyi]
recip = recip/bs
fr += d[xyi,gi] * recip
next gi

x[xyi] = xcenter + sin(pi2 * fr) * radius
y[xyi] = ycenter + cos(pi2 * fr) * radius

endproc

Dinc(i1) =

d[i1,1]++;
if d[i1,1] == base[i1] then

i2 = 1

while d[i1,i2] == base[i1]

d[i1,i2] = 0
i2++;
d[i1,i2]++;

endwhile

if i2 > di[i1] then di[i1] = i2 endif

endif

endproc

Drawfigure =

base = x = y = di = array(2)
d = array(2,100)
radius = 100
pi2 = pi * 2
base[1] = 2
base[2] = 6
di[1] = 1
di[2] = 1

while true

for i = 1 to 2
call Dinc(i)
call GetXY(i)
next i

plot (x[1]+x[2]) / 2, (y[1] + y[2]) / 2

endwhile

endproc

call drawfigure

Pirouetting the Perimeter

by in Geometry, Mathematics, Triangles and tagged , , , , , , , | Leave a comment

Imagine a ballerina pirouetting on the perimeter of an equilateral triangle. Suppose that her armlength is half the radius of the circumscribed circle. If her right arm is represented in green and her right hand in yellow, this is one path that her right hand might trace, depending on the relative speeds of her feet and her pirouettes:

The perimeter of an equilateral triangle

A ballerina pirouetting on the perimeter stage #1

Perimeter pirouette #2

Perimeter pirouette #3

Perimeter pirouette #4

Perimeter pirouette #5

Perimeter pirouette #6

Perimeter pirouette #7

Perimeter pirouette #8

Perimeter pirouette #9

Perimeter pirouette #10

[…]

↓

[…]

Perimeter pirouette #128

Perimeter pirouettes (animated)

The right hand of the ballerina during the pirouettes

The full path traced by the ballerina’s right hand

The paths change as you adjust speed and direction (clockwise or anticlockwise) of the pirouettes, the armlength of the ballerina, and so on:

speed = 0.5 (pirouettes)

speed = 0.5 (path)

speed = -1 (anticlockwise pirouettes)

speed = -1 (path)

speed = 1, armlength = 1/3 (pirouettes)

speed = 1, armlength = 1/3 (path)

speed = -0.5 (pirouettes)

speed = -0.5 (path)

speed = -0.75 (pirouettes)

speed = -0.75 (path)

And what about the paths produced by pirouettes on the perimeters of other polygons? Watch this space.