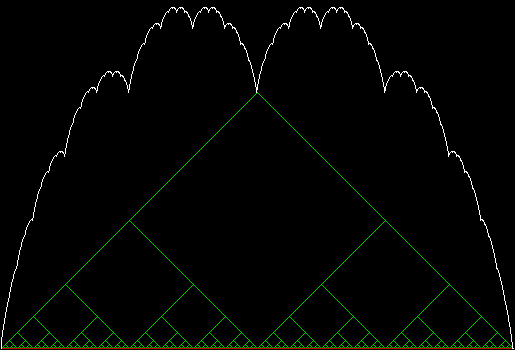
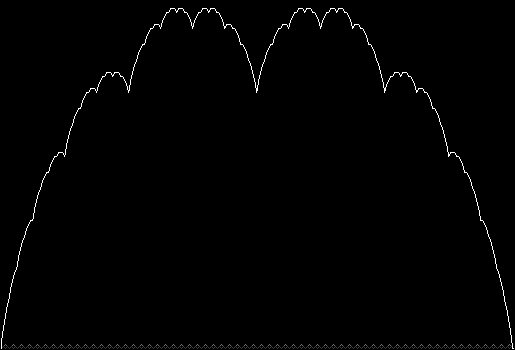
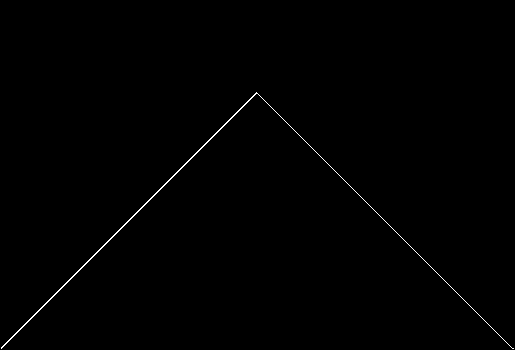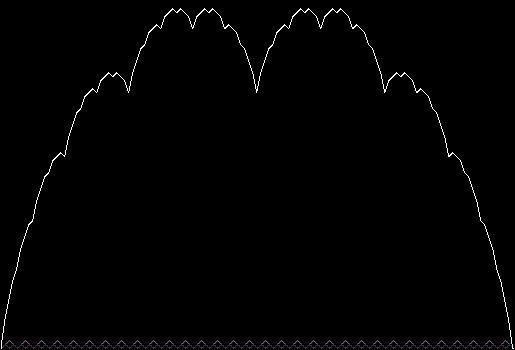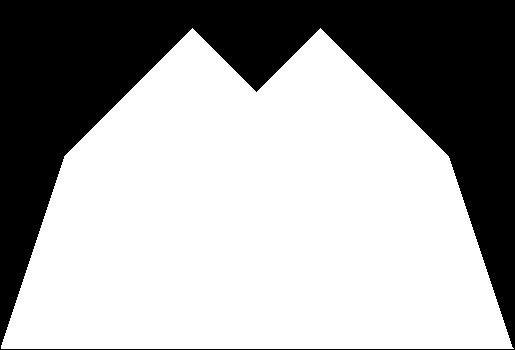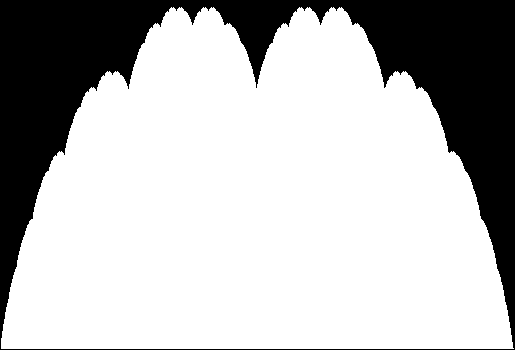
The blancmange curve is an interesting fractal formed by summing a series of zigzags. It
takes its name from its resemblance to the milk-pudding known as a blancmange
(blanc-manger in French, meaning “white eating”):

Blancmange curve

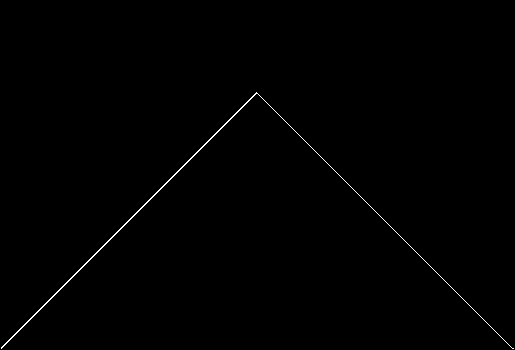
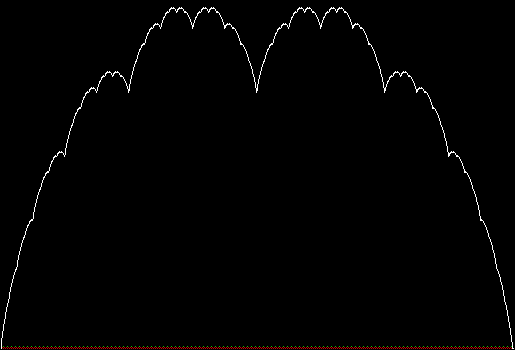
In successive zigzags, the number of zags doubles as their height halves, i.e. z(i) = z(i-1) * 2, h(i) = h(i-1) / 2. If all the zigzags are represented at once, the construction looks like this:

Zigzags 1 to 10

Zigzags 1 to 10 (animated)

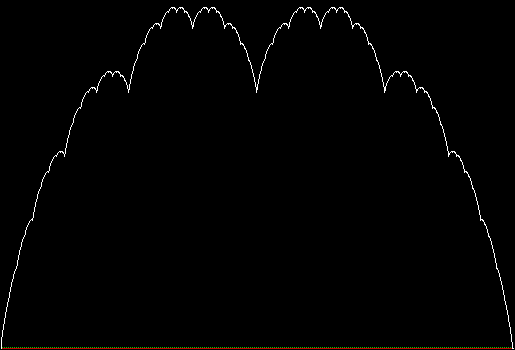
Here is a step-by-step construction, with the total sum of zigzags in white, the present zigzag in red and the previous zigzag in green:

Blancmange curve stage 1

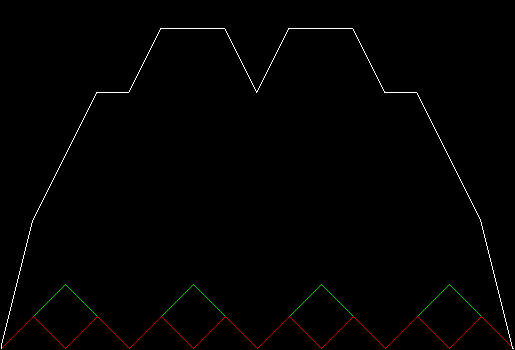
Stage 2

Stage 3

Stage 4

Stage 5

Stage 6

Stage 7

Stage 8

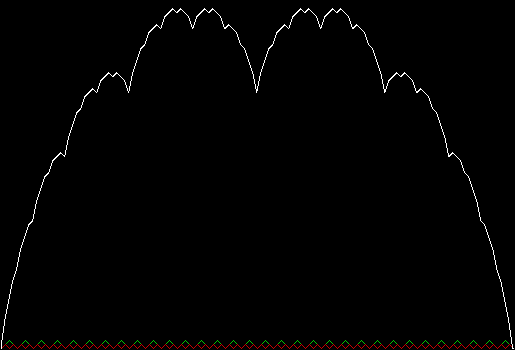
Stage 9

Stage 10

Blancmange curve (animated)

It’s easy to think of variants on the standard blancmange curve. Suppose the number of zags triples as their height is divided by three, i.e. z(i) = z(i-1) * 3, h(i) = h(i-1) / 3:

Blancmange curve for z(i) = z(i-1) * 3, h(i) = h(i-1) / 3

Continue reading “White Rites”…