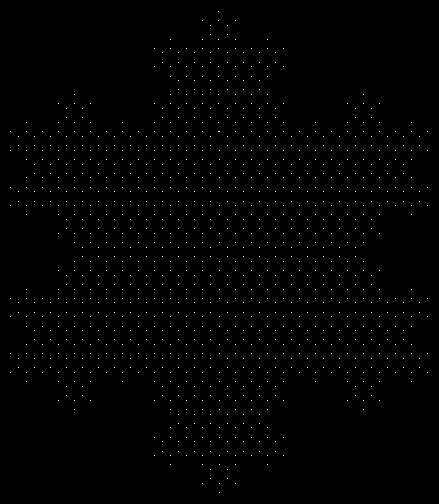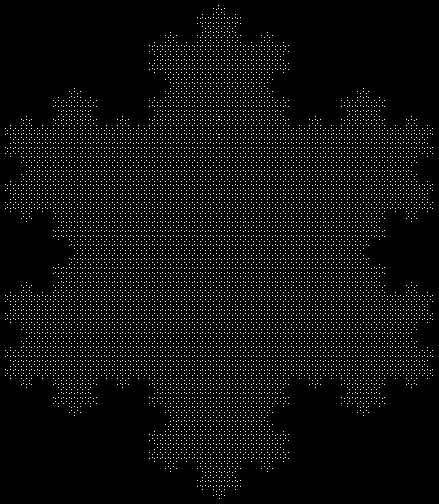In “Diamonds to Dust”, I showed how the Mitsubishi logo could be turned into a fractal, like this:
The Mitsubishi diamonds (source)
↓
↓
Mitsubishi logo to fractal (animated)
Now I want to look at another famous symbol and its fractalization. Here’s the symbol, the hexagram:

Hexagram, a six-pointed star
The hexagram can be dissected into twelve equilateral triangles like this:

Hexagram dissected into 12 equilateral triangles
If each triangle in the dissection is replaced by a hexagram, then the hexagram is dissected again into twelve triangles, you get a famous fractal, the Koch snowflake:
The Koch snowflake
The Koch snowflake again
Hexagram to Koch snowflake (animated)
If you color the triangles, you get something like this:
Colored hexagram to fractal (animated)
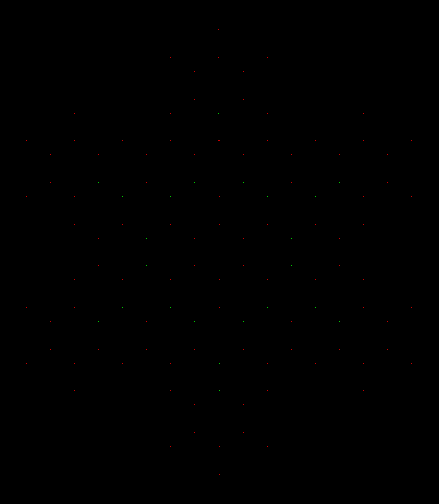
Of course, this is a very inefficient way to create a Koch snowflake, because the interior hexagrams consume processing time while not contributing to the fractal boundary of the snowflake. But in a way you can fully fractalize the hexagram if you draw only the point at the center of each triangle and then color it according to how many times the pixel in question has been drawn on before. To see how this works, first look at what happens when the center-points are represented in white:
White center-points (animated)
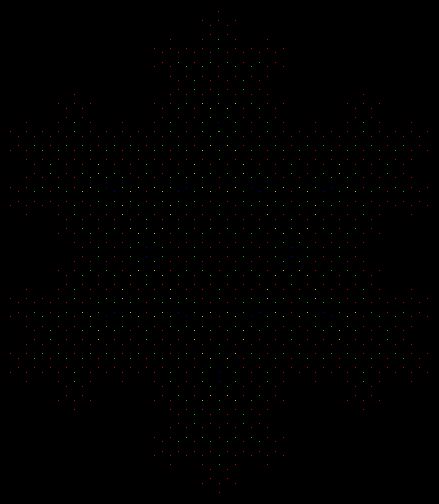
And here’s the fully fractalized hexagram, with colored center-points:
Colored center-points (animated)
Previously Pre-Posted…
• The Hex Fractor #1 — hexagons and fractals
• The Hex Fractor #2 — hexagons and fractals again
• Diamonds to Dust — turning the Mitsubishi logo into a fractal