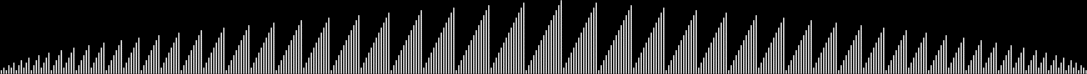Monthly Archives: April 2025

Mathematicoynte

by in Arithmetic, Continued Fractions, Fractals, Mathematics and tagged , , , , , , , , | Leave a comment

Pre-previously, I looked at a fractal phallus. Now I want to look at a fractal fanny (in the older British sense). In fact, it’s a fractional fractal fanny. Take a look at these fractions:


1/10, 1/9, 1/8, 1/7, 1/6, 1/5, 2/10, 2/9, 1/4, 2/8, 2/7, 3/10, 1/3, 2/6, 3/9, 3/8, 2/5, 4/10, 3/7, 4/9, 1/2, 2/4, 3/6, 4/8, 5/10, 5/9, 4/7, 3/5, 6/10, 5/8, 2/3, 4/6, 6/9, 7/10, 5/7, 3/4, 6/8, 7/9, 4/5, 8/10, 5/6, 6/7, 7/8, 8/9, 9/10

They’re all the fractions for 1/2..(n-1)/n, n = 10, sorted by increasing size. But obviously some of them are the same: 1/2 = 2/4 = 3/6 = 5/10, 1/3 = 2/6 = 3/9, 1/4 = 2/8, and so on. If you remove the duplicates, you get this set of reduced fractions:


1/10, 1/9, 1/8, 1/7, 1/6, 1/5, 2/9, 1/4, 2/7, 3/10, 1/3, 3/8, 2/5, 3/7, 4/9, 1/2, 5/9, 4/7, 3/5, 5/8, 2/3, 7/10, 5/7, 3/4, 7/9, 4/5, 5/6, 6/7, 7/8, 8/9, 9/10

Now here are the reduced fractions for 1/2..(n-1)/n, n = 30:


1/30, 1/29, 1/28, 1/27, 1/26, 1/25, 1/24, 1/23, 1/22, 1/21, 1/20, 1/19, 1/18, 1/17, 1/16, 1/15, 2/29, 1/14, 2/27, 1/13, 2/25, 1/12, 2/23, 1/11, 2/21, 1/10, 3/29, 2/19, 3/28, 1/9, 3/26, 2/17, 3/25, 1/8, 3/23, 2/15, 3/22, 4/29, 1/7, 4/27, 3/20, 2/13, 3/19, 4/25, 1/6, 5/29, 4/23, 3/17, 5/28, 2/11, 5/27, 3/16, 4/21, 5/26, 1/5, 6/29, 5/24, 4/19, 3/14, 5/23, 2/9, 5/22, 3/13, 7/30, 4/17, 5/21, 6/25, 7/29, 1/4, 7/27, 6/23, 5/19, 4/15, 7/26, 3/11, 8/29, 5/18, 7/25, 2/7, 7/24, 5/17, 8/27, 3/10, 7/23, 4/13, 9/29, 5/16, 6/19, 7/22, 8/25, 9/28, 1/3, 10/29, 9/26, 8/23, 7/20, 6/17, 5/14, 9/25, 4/11, 11/30, 7/19, 10/27, 3/8, 11/29, 8/21, 5/13, 7/18, 9/23, 11/28, 2/5, 11/27, 9/22, 7/17, 12/29, 5/12, 8/19, 11/26, 3/7, 13/30, 10/23, 7/16, 11/25, 4/9, 13/29, 9/20, 5/11, 11/24, 6/13, 13/28, 7/15, 8/17, 9/19, 10/21, 11/23, 12/25, 13/27, 14/29, 1/2, 15/29, 14/27, 13/25, 12/23, 11/21, 10/19, 9/17, 8/15, 15/28, 7/13, 13/24, 6/11, 11/20, 16/29, 5/9, 14/25, 9/16, 13/23, 17/30, 4/7, 15/26, 11/19, 7/12, 17/29, 10/17, 13/22, 16/27, 3/5, 17/28, 14/23, 11/18, 8/13, 13/21, 18/29, 5/8, 17/27, 12/19, 19/30, 7/11, 16/25, 9/14, 11/17, 13/20, 15/23, 17/26, 19/29, 2/3, 19/28, 17/25, 15/22, 13/19, 11/16, 20/29, 9/13, 16/23, 7/10, 19/27, 12/17, 17/24, 5/7, 18/25, 13/18, 21/29, 8/11, 19/26, 11/15, 14/19, 17/23, 20/27, 3/4, 22/29, 19/25, 16/21, 13/17, 23/30, 10/13, 17/22, 7/9, 18/23, 11/14, 15/19, 19/24, 23/29, 4/5, 21/26, 17/21, 13/16, 22/27, 9/11, 23/28, 14/17, 19/23, 24/29, 5/6, 21/25, 16/19, 11/13, 17/20, 23/27, 6/7, 25/29, 19/22, 13/15, 20/23, 7/8, 22/25, 15/17, 23/26, 8/9, 25/28, 17/19, 26/29, 9/10, 19/21, 10/11, 21/23, 11/12, 23/25, 12/13, 25/27, 13/14, 27/29, 14/15, 15/16, 16/17, 17/18, 18/19, 19/20, 20/21, 21/22, 22/23, 23/24, 24/25, 25/26, 26/27, 27/28, 28/29, 29/30

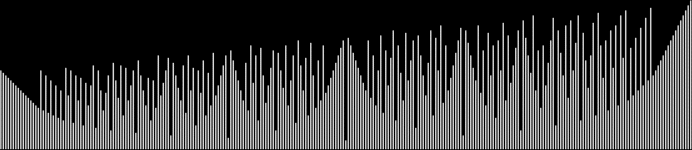
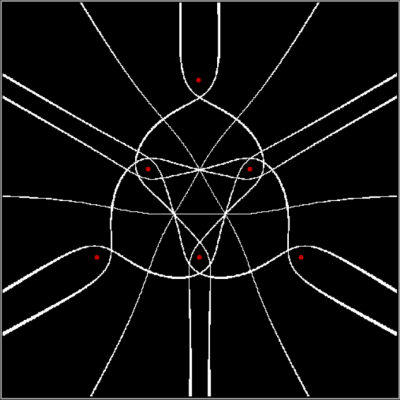
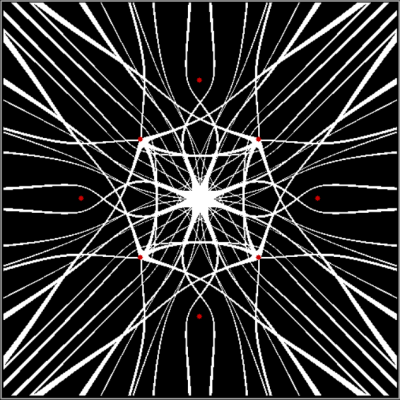
Can you see the fractal fanny? Not unless you’re superhuman. But any normal human can see the fractal fanny when you turn those reduced and sorted fractions, a/b, into a graph, where y = b and x = n for a/bn:

graph for b of reduced a/b = 1/2..29/30, sorted by size of a/b

(click for larger)

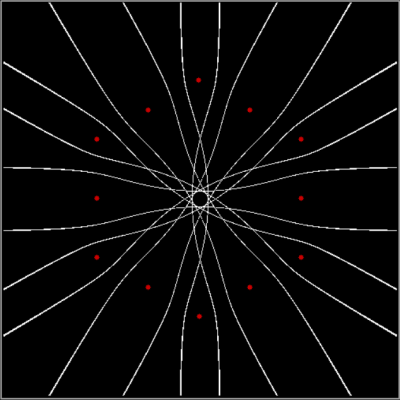
If you don’t reduce the fractions, you get this distorted coynte:

graph for b of all fractions 1/2..29/30, sorted by a/b

And you can use other variables for y, like the sum of the continued fraction of a/b:

graph for sum(contfrac(a/b)) of reduced fractions 1/2..29/30, sorted by a/b

graph for cfsum of all fractions 1/2..29/30, sorted by a/b

And the product of the continued fraction of a/b:

graph for prod(contfrac(a/b)) of reduced fractions 1/2..29/30, sorted by a/b

graph for cfmul of all fractions 1/2..29/30, sorted by a/b

And you can sort by the size of other variables, like the number of factors of b:

graph for a+b of all fractions 1/2..29/30, sorted by factornum(b)

And so on:

graph for a of reduced fractions 1/2..29/30, sorted by a/b

graph for a of reduced fractions 1/2..29/30, sorted by a/b

graph for a of all fractions 1/2..29/30, sorted by a/b

graph for a of all fractions 1/2..29/30, sorted by length(contfrac(a/b))

graph for a of all fractions 1/2..29/30, sorted by factornum(b)

graph for a of all fractions 1/2..29/30, sorted by gcd(a/b)

graph for a+b of all fractions 1/2..29/30, sorted by a/b

graph for a+b of reduced fractions 1/2..29/30, sorted by a/b

graph for a+b of all fractions 1/2..29/30, sorted by a+b

graph for a+b of all fractions 1/2..29/30, sorted by cflen(a/b)

graph for a+b of all fractions 1/2..29/30, sorted by gbd(a,b)

graph for b of all fractions 1/2..29/30, sorted by a+b

graph for b of all fractions 1/2..29/30, sorted by cflen(a/b)

graph for b of all fractions 1/2..29/30, sorted by factnum(b)

graph for b of all fractions 1/2..29/30, sorted by gcd(a,b)

graph for b-a of all fractions 1/2..29/30, sorted by a/b

graph for b-a of reduced fractions 1/2..29/30, sorted by a/b

graph for b-a of all fractions 1/2..29/30, sorted by a+b

graph for b-a of all fractions 1/2..29/30, sorted by factnum(b)

graph for cfmul of all fractions 1/2..29/30, sorted by a

graph for cfsum of all fractions 1/2..29/30, sorted by a

Previously Pre-Posted (Please Peruse)

• Phrallic Frolics — a look at fractal phalluses, a.k.a. phralluses

Penny’s Petrified Parade

by in 2SLGBTQ+ Community Issues, English Usage, Guardianistas, Mixed Metaphors, Politics and tagged , , , , , , , | Leave a comment

“Without political agitation, sex can always be co-opted, calcifying gender revolution into another weary parade of saleable binary stereotypes.” — Laurie Penny, Meat Market: Female Flesh Under Capitalism (2011)

Points Pared

by in Geometry, Hexagons, Mathematics, Squares, Triangles and tagged , , , , , , | Leave a comment

There are an infinite number of points in the plane. And in part of the plane. So you have to pare points to create interesting shapes. And one way of paring them is by comparing them. The six red dots in the image below mark the three vertices of an equilateral triangle and the three mid-points of the sides. Now, test the other points in the surrounding plane and mark them in white if the average distance to (the centers of) any two of the red dots is equal to the average distance to (the centers of) the four other red dots:

Triangle + 1 side-point, sum(d1,d2)/2 = sum(d3,d4,d5,d6)/4

(click for larger)

Add a central red dot to the triangle and you get this pattern:

Triangle + 1 side-point + center, distfunc(2) = distfunc(5)

And so on:

v = 3 + sd = 2, distfunc(2) = distfunc(7)

v = 3 + sd = 2 + center, distfunc(2) = distfunc(7)

v = 3 + sd = 1, distfunc(3) = distfunc(3)

v = 3 + sd = 1 + center, distfunc(3) = distfunc(7)

v = 4 + center, distfunc(2) = distfunc(3)

v = 4 + sd = 1, distfunc(2) = distfunc(6)

v = 4 + sd = 1 + center, distfunc(2) = distfunc(7)

v = 4 + sd = 2, distfunc(2) = distfunc(10)

v = 4 + sd = 2, distfunc(2) = distfunc(10) (enlarged)

v = 4 + sd = 1, distfunc(3) = distfunc(5)

v = 4 + sd = 1, distfunc(4) = distfunc(4)

v = 5 + sd = 1, distfunc(2) = distfunc(8)

v = 5 + sd = 1, distfunc(2) = distfunc(8) (smaller scale)

v = 6 + sd = 1, distfunc(1) = distfunc(11)

v = 6 + sd = 1 + center, distfunc(1) = distfunc(12)

v = 6, distfunc(2) = distfunc(4)

v = 6 + center, distfunc(2) = distfunc(5)

v = 6, distfunc(3) = distfunc(3)

v = 6 + center, distfunc(3) = distfunc(4)

Gull-Om, Gull-Un

by in Aesthetics, Album Art and tagged , , , , , , , , | Leave a comment

Cover of Variations on a Theme (2005) by Om

Cover of Yr Wylan Ddu (1996) by Slow Exploding Gulls

Elsewhere Other-Accessible…

• Om Vibratory — Om’s official site
• Mental Marine Music — an introduction to Slow Exploding Gulls

The Call of CFulhu

by in Arithmetic, √2, Continued Fractions, Fibonacci Sequence, H.P. Lovecraft, Integer Sequences, φ, Mathematics, Phi, Square root of 2 and tagged , , , , , | Leave a comment

“The most merciful thing in the world, I think, is the inability of the human mind to correlate all its contents.” So said HPL in “The Call of Cthulhu” (1926). But I’d still like to correlate the contents of mine a bit better. For example, I knew that φ, the golden ratio, is the most irrational of all numbers, in that it is the slowest to be approximated with rational fractions. And I also knew that continued fractions, or CFs, were a way of representing both rationals and irrationals as a string of numbers, like this:

contfrac(10/7) = [1; 2, 3]
10/7 = 1 + 1/(2 + 1/3)
10/7 = 1.428571428571…

contfrac(3/5) = [0; 1, 1, 2]
4/5 = 0 + 1/(1 + 1/(1 + 1/2))
4/5 = 0.8

contfrac(11/8) = [1; 2, 1, 2]
11/8 = 1 + 1/(2 + 1/(1 + 1/2))
11/8 = 1.375

contfrac(4/7) = [0; 1, 1, 3]
4/7 = 0 + 1/(1 + 1/(1 + 1/3))
4/7 = 0.57142857142…

contfrac(17/19) = [0; 1, 8, 2]
17/19 = 0 + 1/(1 + 1/(8 + 1/2))
17/19 = 0.8947368421052…

contfrac(8/25) = [0; 3, 8]
8/25 = 0 + 1/(3 + 1/8)
8/25 = 0.32

contfrac(√2) = [1; 2, 2, 2, 2, 2, 2, 2…] = [1; 2]

√2 = 1 + 1/(2 + 1/(2 + 1/(2 + 1/(2 + 1/(2 + 1/(2 + 1/2 + …))))))

√2 = 1.41421356237309504…

contfrac(φ) = [1; 1, 1, 1, 1, 1, 1, 1, 1…]

φ = 1/(1 + 1/(1 + 1/(1 + 1/(1 + 1/(1 + 1/(1 + 1/(1 + 1/1 + …)))))))

φ = 1.6180339887498948…

But I didn’t correlate those two contents of my mind: the maximal irrationality of φ and the way continued fractions work.

That’s why I was surprised when I was looking at the continued fractions of 2..(n-1) / n for 3,4,5,6,7… That is, I was looking at the continued fractions of 2/3, 3/4, 2/5, 3/5, 4/5, 5/6, 2/7, 3/7… (skipping fractions like 2/4, 2/6, 3/6 etc, because they’re reducible: 2/4 = ½, 2/6 = 1/3, 3/6 = ½ etc). I wondered which fractions set successive records for the length of their continued fractions as one worked through ½, 2/3, 3/4, 2/5, 3/5, 4/5, 5/6, 2/7, 3/7… And because I hadn’t correlated the contents of my mind, I was surprised at the result. I shouldn’t have been, of course:

contfrac(1/2) = [0; 2] (cfl=1)
1/2 = 0 + 1/2
1/2 = 0.5

contfrac(2/3) = [0; 1, 2] (cfl=2)
2/3 = 0 + 1/(1 + 1/2)
2/3 = 0.666666666…

contfrac(3/5) = [0; 1, 1, 2] (cfl=3)
3/5 = 0 + 1/(1 + 1/(1 + 1/2))
3/5 = 0.6

contfrac(5/8) = [0; 1, 1, 1, 2] (cfl=4)
5/8 = 0 + 1/(1 + 1/(1 + 1/(1 + 1/2)))
5/8 = 0.625

contfrac(8/13) = [0; 1, 1, 1, 1, 2] (cfl=5)
8/13 = 0 + 1/(1 + 1/(1 + 1/(1 + 1/(1 + 1/2))))
8/13 = 0.615384615…

contfrac(13/21) = [0; 1, 1, 1, 1, 1, 2] (cfl=6)
13/21 = 0 + 1/(1 + 1/(1 + 1/(1 + 1/(1 + 1/(1 + 1/2)))))
13/21 = 0.619047619…

contfrac(21/34) = [0; 1, 1, 1, 1, 1, 1, 2] (cfl=7)
21/34 = 0 + 1/(1 + 1/(1 + 1/(1 + 1/(1 + 1/(1 + 1/(1 + 1/2))))))
21/34 = 0.617647059…

contfrac(34/55) = [0; 1, 1, 1, 1, 1, 1, 1, 2] (cfl=8)
contfrac(55/89) = [0; 1, 1, 1, 1, 1, 1, 1, 1, 2] (cfl=9)
contfrac(89/144) = [0; 1, 1, 1, 1, 1, 1, 1, 1, 1, 2] (cfl=10)
contfrac(144/233) = [0; 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 2] (cfl=11)
contfrac(233/377) = [0; 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 2] (cfl=12)
contfrac(377/610) = [0; 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 2] (cfl=13)
contfrac(610/987) = [0; 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 2] (cfl=14)
contfrac(987/1597) = [0; 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 2] (cfl=15)
contfrac(1597/2584) = [0; 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 2] (cfl=16)
contfrac(2584/4181) = [0; 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 2] (cfl=17)
contfrac(4181/6765) = [0; 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 2] (cfl=18)
[…]

Which n1/n2 set records for the length of their continued fractions (with n2 > n1)? It’s the successive Fibonacci fractions, fib(i)/fib(i+1), of course. I didn’t anticipate that answer because I didn’t understand φ and continued fractions properly. And I still don’t, because I’ve been surprised again today looking at palindromic CFs like these:

contfrac(2/5) = [0; 2, 2] (cfl=2)
2/5 = 0 + 1/(2 + 1/2)
2/5 = 0.4

contfrac(3/8) = [0; 2, 1, 2] (cfl=3)
3/8 = 0 + 1/(2 + 1/(1 + 1/2))
3/8 = 0.375

contfrac(3/10) = [0; 3, 3] (cfl=2)
3/10 = 0 + 1/(3 + 1/3)
3/10 = 0.3

contfrac(5/12) = [0; 2, 2, 2] (cfl=3)
5/12 = 0 + 1/(2 + 1/(2 + 1/2))
5/12 = 0.416666666…

contfrac(5/13) = [0; 2, 1, 1, 2] (cfl=4)
5/13 = 0 + 1/(2 + 1/(1 + 1/(1 + 1/2)))
5/13 = 0.384615384…

contfrac(4/15) = [0; 3, 1, 3] (cfl=3)
4/15 = 0 + 1/(3 + 1/(1 + 1/3))
4/15 = 0.266666666…

contfrac(7/16) = [0; 2, 3, 2] (cfl=3)
7/16 = 0 + 1/(2 + 1/(3 + 1/2))
7/16 = 0.4375

contfrac(4/17) = [0; 4, 4] (cfl=2)
4/17 = 0 + 1/(4 + 1/4)
4/17 = 0.235294117…

Again, I wondered which of these fractions set successive records for the length of their palindromic continued fractions. Here’s the answer:

contfrac(1/2) = [0; 2] (cfl=1)
1/2 = 0 + 1/2
1/2 = 0.5

contfrac(2/5) = [0; 2, 2] (cfl=2)
2/5 = 0 + 1/(2 + 1/2)
2/5 = 0.4

contfrac(3/8) = [0; 2, 1, 2] (cfl=3)
3/8 = 0 + 1/(2 + 1/(1 + 1/2))
3/8 = 0.375

contfrac(5/13) = [0; 2, 1, 1, 2] (cfl=4)
5/13 = 0 + 1/(2 + 1/(1 + 1/(1 + 1/2)))
5/13 = 0.384615384…

contfrac(8/21) = [0; 2, 1, 1, 1, 2] (cfl=5)
8/21 = 0 + 1/(2 + 1/(1 + 1/(1 + 1/(1 + 1/2))))
8/21 = 0.380952380…

contfrac(13/34) = [0; 2, 1, 1, 1, 1, 2] (cfl=6)
13/34 = 0 + 1/(2 + 1/(1 + 1/(1 + 1/(
1 + 1/(1 + 1/2)))))
13/34 = 0.382352941..

contfrac(21/55) = [0; 2, 1, 1, 1, 1, 1, 2] (cfl=7)
21/55 = 0 + 1/(2 + 1/(1 + 1/(1 + 1/(1 + 1/(1 + 1/(1 + 1/2))))))
21/55 = 0.381818181…

contfrac(34/89) = [0; 2, 1, 1, 1, 1, 1, 1, 2] (cfl=8)
contfrac(55/144) = [0; 2, 1, 1, 1, 1, 1, 1, 1, 2] (cfl=9)
contfrac(89/233) = [0; 2, 1, 1, 1, 1, 1, 1, 1, 1, 2] (cfl=10)
contfrac(144/377) = [0; 2, 1, 1, 1, 1, 1, 1, 1, 1, 1, 2] (cfl=11)
contfrac(233/610) = [0; 2, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 2] (cfl=12)
contfrac(377/987) = [0; 2, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 2] (cfl=13)
contfrac(610/1597) = [0; 2, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 2] (cfl=14)
contfrac(987/2584) = [0; 2, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 2] (cfl=15)
contfrac(1597/4181) = [0; 2, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 2] (cfl=16)
contfrac(2584/6765) = [0; 2, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 2] (cfl=17)
[…]

Now it’s the successive Fibonacci skip-one fractions, fib(i)/fib(i+2), that set records for the length of their palindromic continued fractions. But I think you’d have to be very good at maths not to be surprised by that result.

After that, I continued to be compelled by the Call of CFulhu and started to look at the CFs of Fibonacci skip-n fractions in general. That’s contfrac(fib(i)/fib(i+n)) for n = 1,2,3,… And I’ve found more interesting patterns, as I’ll describe in a follow-up post.

Viler Smiler

by in A.E. Housman, English Usage, Language, Literature, Poetry and tagged , , , , , , , , | 1 Comment

Less is more. It’s a principle for good writing, not an unalterable law. And one of the best expositions of the principle was given by A.E. Housman in his lecture “The Name and Nature of Poetry” (1933):

Dryden’s translation [of The Canterbury Tales] shows Dryden in the maturity of his power and accomplishment, and much of it can be honestly and soberly admired. Nor was he insensible to all the peculiar excellence of Chaucer: he had the wit to keep unchanged such lines as ‘Up rose the sun and up rose Emily’ or ‘The slayer of himself yet saw I there’; he understood that neither he nor anyone else could better them. But much too often in a like case he would try to improve, because he thought that he could. He believed, as he says himself, that he was ‘turning some of the Canterbury Tales into our language, as it is now refined’; ‘the words’ he says again ‘are given up as a post not to be defended in our poet, because he wanted the modern art of fortifying’; ‘in some places’ he tells us ‘I have added somewhat of my own where I thought my author was deficient, and had not given his thoughts their true lustre, for want of words in the beginning of our language’.

Let us look at the consequences. Chaucer’s vivid and memorable line

The smiler with the knife under the cloke

becomes these three:

Next stood Hypocrisy, with holy leer,
Soft smiling and demurely looking down,
But hid the dagger underneath the gown.

Again:

Alas, quod he, that day that I was bore.

So Chaucer, for want of words in the beginning of our language. Dryden comes to his assistance and gives his thoughts their true lustre thus:

Cursed be the day when first I did appear;
Let it be blotted from the calendar,
Lest it pollute the month and poison all the year.

Or yet again:

The queen anon for very womanhead
Gan for to weep, and so did Emily
And all the ladies in the company.

If Homer or Dante had the same thing to say, would he wish to say it otherwise? But to Dryden Chaucer wanted the modern art of fortifying, which he thus applies:

He said; dumb sorrow seized the standers-by.
The queen, above the rest, by nature good
(The pattern formed of perfect womanhood)
For tender pity wept: when she began
Through the bright quire the infectious virtue ran.
All dropped their tears, even the contended maid.

• “The Name and Nature of Poetry” (1933) by A.E. Housman — more of “less is more”

So, In Terms of Transgenderism…

by in 2SLGBTQ+ Community Issues, Guardianistas, In Terms Of, Transgression... and tagged , , , , , , , , , , , , , , , | Leave a comment

Beth Rigby, Sky News: This is an image we’ve seen a lot of recently, it’s a podium with a trans woman coming first and a biological women coming second and third. Do you think that’s fair, Ian?

Ian Anderson of Stonewall: So, sport by sport, people are looking at this. On elite sport, what you’re finding is that sporting body by sporting body is looking at this issue.

BR: Let me put it another way, how would you feel if you were number two and three in that scenario? Do you think that was fair?

IA: Well, I’m absolutely rubbish at sport.

BR: You know what I mean. How do you think this woman, this woman might feel about that?

IA: Yeah, so, I mean, everybody, we’re working our way through on this, this is, I mean, this is, I mean, how trans folk take part in elite sport.

BR: But this is a problem, isn’t it? Do you see this as a problem?

IA: So, I think it’s a problem in terms of the perception of the conversation.

[etc]

• “The Idiocy of Stonewall”, Julie Bindel