Category Archives: Arithmetic

Sequence Unfurls…

by in Arithmetic, Egyptian Fractions, Fibonacci Sequence, Integer Sequences, Mathematics and tagged , , , , | Leave a comment

The Fibonacci sequence is beautiful like clockwork. There’s a perfectly clear, rigorously defined mechanism ticking out an entirely predictable result for ever:

0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946, 17711, 28657, 46368, 75025, 121393, 196418, 317811, 514229, 832040, 1346269, 2178309, 3524578, 5702887, 9227465, 14930352, 24157817, 39088169, 63245986, 102334155, … — A000045 at the Online Encyclopedia of Integer Sequences (OEIS)

And there’s a formula to calculate any term in the sequence without calculating all the terms that precede it:

Binet’s formula for Fn, the n-th Fibonacci number

But I also like sequences that you might call definitely arbitrary. That is, there’s a perfectly clear, rigorously defined mechanism, but the results seem arbitrary — not predictable at all:

6, 15, 5, 22, 6, 3, 30, 9, 7, 2, 45, 15, 6, 5, 1, 36, 14, 6, 5, 3, 1, 62, 22, 16, 6, 5, 3, 2, 69, 21, 15, 4, 9, 5, 2, 1, 84, 30, 15, 9, 6, 7, 2, 2, 1, 56, 22, 13, 7, 3, 5, 2, 0, 0, 0, 142, 45, 22, 15, 12, 6, 9, 5, 3, 1, 2, 53, 17, 8, 4, 5, 1, 6, 3, 1, 1, 1, 0, 124, 36, 27, 14, 18, 6, 6, 5, 2, 3, 1, 1, 0, … A349083 at OEIS

What’s the formula there? That sequence is defined at the OEIS as “The number of three-term Egyptian fractions of rational numbers x/y, 0 < x/y < 1, ordered as below. The sequence is the number of (p,q,r) such that x/y = 1/p + 1/q + 1/r where p, q, and r are integers with p < q < r.” For example: “The sixth rational number is 3/4 [and] 3/4 = 1/2 + 1/5 + 1/20 = 1/2 + 1/6 + 1/12 = 1/3 + 1/4 + 1/5, so a(6)=3.”

The Number of the Decreased

by in 666, Arithmetic, Mathematics, Number of the Beast and tagged , , , , , , , | Leave a comment

I wondered what happened when you take a fraction, a/b, and calculate a/b – (a/b)^2 = c/d. And an interesting pattern appeared when I tried a prime denominator and all numerators less than that denominator. Here’s the pattern with the prime denominator of 7:


1/7 - 01/49 = 06/49
2/7 - 04/49 = 10/49
3/7 - 09/49 = 12/49
4/7 - 16/49 = 12/49
5/7 - 25/49 = 10/49
6/7 - 36/49 = 06/49

And here it is with the prime denominator of 13:


01/13 - 001/169 = 12/169
02/13 - 004/169 = 22/169
03/13 - 009/169 = 30/169
04/13 - 016/169 = 36/169
05/13 - 025/169 = 40/169
06/13 - 036/169 = 42/169
07/13 - 049/169 = 42/169
08/13 - 064/169 = 40/169
09/13 - 081/169 = 36/169
10/13 - 100/169 = 30/169
11/13 - 121/169 = 22/169
12/13 - 144/169 = 12/169

It’s easier to see what’s going on with the smaller denominator:


1/7 - 01/49 = 06/49 = 1/7 - (1/7)^2
2/7 - 04/49 = 10/49 = 2/7 - (2/7)^2
3/7 - 09/49 = 12/49 = 3/7 - (3/7)^2
4/7 - 16/49 = 12/49
5/7 - 25/49 = 10/49
6/7 - 36/49 = 06/49

1/7 - 01/49 = 07/49 - 01/49 = 06/49
2/7 - 04/49 = 14/49 - 04/49 = 10/49
3/7 - 09/49 = 21/49 - 09/49 = 12/49
4/7 - 16/49 = 28/49 - 16/49 = 12/49
5/7 - 25/49 = 35/49 - 25/49 = 10/49
6/7 - 36/49 = 42/49 - 36/49 = 06/49

1/7 - 01/49 = 1*7/7^2 - 1^2/7^2 = 07/49 - 01/49 = 06/49
2/7 - 04/49 = 2*7/7^2 - 2^2/7^2 = 14/49 - 04/49 = 10/49
3/7 - 09/49 = 3*7/7^2 - 3^2/7^2 = 21/49 - 09/49 = 12/49
4/7 - 16/49 = 4*7/7^2 - 4^2/7^2 = 28/49 - 16/49 = 12/49
5/7 - 25/49 = 5*7/7^2 - 5^2/7^2 = 35/49 - 25/49 = 10/49
6/7 - 36/49 = 6*7/7^2 - 6^2/7^2 = 42/49 - 36/49 = 06/49

Here’s a set of the patterns using prime denominators from 3 to 13:


1/3 - 1/9 = 2/9
2/3 - 4/9 = 2/9

1/5 - 01/25 = 4/25
2/5 - 04/25 = 6/25
3/5 - 09/25 = 6/25
4/5 - 16/25 = 4/25

1/7 - 01/49 = 06/49
2/7 - 04/49 = 10/49
3/7 - 09/49 = 12/49
4/7 - 16/49 = 12/49
5/7 - 25/49 = 10/49
6/7 - 36/49 = 06/49

01/11 - 001/121 = 10/121
02/11 - 004/121 = 18/121
03/11 - 009/121 = 24/121
04/11 - 016/121 = 28/121
05/11 - 025/121 = 30/121
06/11 - 036/121 = 30/121
07/11 - 049/121 = 28/121
08/11 - 064/121 = 24/121
09/11 - 081/121 = 18/121
10/11 - 100/121 = 10/121

01/13 - 001/169 = 12/169
02/13 - 004/169 = 22/169
03/13 - 009/169 = 30/169
04/13 - 016/169 = 36/169
05/13 - 025/169 = 40/169
06/13 - 036/169 = 42/169
07/13 - 049/169 = 42/169
08/13 - 064/169 = 40/169
09/13 - 081/169 = 36/169
10/13 - 100/169 = 30/169
11/13 - 121/169 = 22/169
12/13 - 144/169 = 12/169

Then I tried a/b – (a/b)^3. There were no obvious strong patterns, but something caught my eye in the last subtraction for b = 19:


01/19 - 0001/6859 = 0360/6859 = 1/19 - (1/19)^3
02/19 - 0008/6859 = 0714/6859 = 2/19 - (2/19)^3
03/19 - 0027/6859 = 1056/6859 = 3/19 - (3/19)^3
04/19 - 0064/6859 = 1380/6859
05/19 - 0125/6859 = 1680/6859
06/19 - 0216/6859 = 1950/6859
07/19 - 0343/6859 = 2184/6859
08/19 - 0512/6859 = 2376/6859
09/19 - 0729/6859 = 2520/6859
10/19 - 1000/6859 = 2610/6859
11/19 - 1331/6859 = 2640/6859
12/19 - 1728/6859 = 2604/6859
13/19 - 2197/6859 = 2496/6859
14/19 - 2744/6859 = 2310/6859
15/19 - 3375/6859 = 2040/6859
16/19 - 4096/6859 = 1680/6859
17/19 - 4913/6859 = 1224/6859
18/19 - 5832/6859 = 0666/6859

Look at the final subtraction: 18/19 – 5832/6859 = 666/6859. So the Number of the Beast is the numerator when 18/19 is decreased by (18/19)^3. Dropping the need for powers of a/b, I looked for more beastly fraction subtractions using pairs of simplified fractions. Here are a few:


26/35 - 04/31 = 666/1085 = 0.613824885...
29/35 - 05/29 = 666/1015 = 0.656157635...
32/35 - 02/23 = 666/0805 = 0.827329193...
40/41 - 14/31 = 666/1271 = 0.523996853...
35/43 - 13/35 = 666/1505 = 0.442524917...
23/47 - 01/31 = 666/1457 = 0.457103638...
30/47 - 12/41 = 666/1927 = 0.345614946...
31/47 - 01/23 = 666/1081 = 0.616096207...
31/47 - 02/46 = 666/1081 = 0.616096207...
40/47 - 02/19 = 666/0893 = 0.745800672...
[...]

This fraction subtraction is beastly in two ways: 95/103 – 83/97 = 666/9991 = 0.066659994…

I also noticed that 666 can be the numerator in two ways when the denominator is 19 and its powers:


18/19 - 5832/6859 = 666/6859 = 18/19 - (18/19)^3
18/19 + 0324/0361 = 666/0361 = 18/19 + (18/19)^2

So 666 is both the Number of the Decreased and the Number of the Increased. That double pattern is general when you either decrease (b-1)/b by ((b-1)/b)^3 or increase (b-1)/b by ((b-1)/b)^2:


2/3 - 8/27 = 10/27 = 2/3 - (2/3)^3
2/3 + 04/9 = 10/09 = 2/3 + (2/3)^2

4/5 - 64/125 = 36/125 = 4/5 - (4/5)^3
4/5 + 16/025 = 36/025 = 4/5 + (4/5)^2

6/7 - 216/343 = 78/343 = 6/7 - (6/7)^2
6/7 + 036/049 = 78/049 = 6/7 + (6/7)^2

10/11 - 1000/1331 = 210/1331
10/11 + 0100/0121 = 210/0121

12/13 - 1728/2197 = 300/2197
12/13 + 0144/0169 = 300/0169

16/17 - 4096/4913 = 528/4913
16/17 + 0256/0289 = 528/0289

18/19 - 5832/6859 = 666/6859
18/19 + 0324/0361 = 666/0361

22/23 - 10648/12167 = 990/12167
22/23 + 00484/00529 = 990/00529

A FracTeasel on a Fract-L

by in Arithmetic, Continued Fractions, Fractals, Mathematics and tagged , , , , , , , , , , , , | Leave a comment

Here are two new fractals, both of which remind me of the seedheads of the wildflower known as a teasel, Dipsacus fullonum:

A FracTeasel fractal

Dried seedheads of teasel, Dipsacus fullonum (Wikipedia)

Another FracTeasel fractal (embedded in the first)

Flowering seedhead of teasel, Dipsacus fullonum (Wikipedia)

How do you create the two FracTeasels? Let’s look first at the fractal they’re inspired by. In “Back to Frac’” I talked about this fractional fractal, a variant of what I call the limestone fractal:

Variant of a limestone fractal or gryke fractal

It’s a fractal on a fract-L, that is, the x and y co-ordinates of the red L represent pairs of fractions generating decimals between 0 and 1. The x represents the fractions a1/b1 = 1/n to (n-1)/n in simplest form: 1/2, 1/3, 2/3, 1/4, 3/4, 1/5, 2/5, 3/5, 4/5, 1/6, 5/6, 1/7, 2/7, 3/7, 4/7, 5/7, 6/7, 1/8, 3/8, 5/8, 7/8,…

And what about the y? It represents the fraction found by taking the continued fraction of a1/b1, reversing it, and generating a new fraction, a2/b2, from the reversal. For example, here’s the continued fraction of a1/b1 = 3/23 = 0.1304347826…:

contfrac(3/23) = 7,1,2

The continued fraction of a1/b1 = 3/23 is used like this to reconstruct a1/b1:

7,1,2

0 → 1 / (0 + 2) = 1/2 → 1 / (1/2 + 1) = 2/3 → 1 / (7 + 2/3) = 3/23

Now reverse the continued fraction, 7,1,2 → 2,1,7, and generate a2/b2:

2,1,7

0 → 1 / (0 + 7) = 1/7 → 1 / (1/7 + 1) = 7/8 → 1 / (2 + 7/8) = 8/23 = 0.3478260869565…

The limestone fractal above appears when a1/b1 → a2/b2 for a1/b1 = 1/2, 1/3, 2/3, 1/4, 3/4, 1/5, 2/5, 3/5, 4/5, 1/6, 5/6, 1/7, 2/7, 3/7, 4/7, 5/7, 6/7, 1/8, 3/8, 5/8, 7/8,… But you can do other things to contfrac(a1/b1) beside just reversing it. What about the permutations of contfrac(a1/b1), for example? If length(contfrac(a1/b1)) = n, the permutations can generate up to n! (factorial n) new a2/b2 for the y co-ordinate (if all the numbers of contfrac(a1/b1) are different, you’ll get n! permutations). The resultant fractal is the first of the FracTeasels above (note that a2/b2 isn’t multipled by two):

FracTeasel #1 from fract-L for y = perm(contfrac(a1/b1))

If you think about it, you’ll see that the fractal from permed contfrac(a1/b1) contains the fractal from reversed contfrac(a1/b1). It also contains the second FracTeasel:

FracTeasel #2

How so? Because the second FracTeasel — let’s call it the stemmed FracTeasel — is created by shifting some numbers in contfrac(a1/b1) and leaving others alone. For example:

contfrac(940/1089) = 1, 6, 3, 4, 5, 2 → 1, 4, 3, 2, 5, 6 = contfrac(1008/1243)

So the function is finding one particular permutation of contfrac(a1/b1) to generate a2/b2, not all permutations. And so the function creates the stemmed FracTeasel, which carries an infinite number of seedheads on the same stem. To show that, here’s an animated gif zooming in on the bend of the fract-L for the stemmed FracTeasel:

Zooming the FracTeasel (animated at ezGif)

Elsewhere Other-Accessible…

• I Like Gryke — a first look at the limestone fractal
• Lime Time — more on the limestone fractal

Matchin’ Fraction

by in Arithmetic, Base Behavior, Continued Fractions, Mathematics, Narcissistic numbers and tagged , , , , | Leave a comment

I wondered whether contfrac(a/b), the continued fraction of a/b, ever matched the digits of a and b in some base. The answer was yes. But I haven’t found any examples in base 10:

3,1,2 = contfrac(3/12) in base 9 = contfrac(3/11) in base 10
4,1,3 = contfrac(4/13) in b16 = contfrac(4/19) in b10
5,1,4 ← 5/14 in b25 = 5/29
6,1,5 ← 6/15 in b36 = 6/41
25,2 ← 2/52 in b9 = 2/47 → 23,2
7,1,6 ← 7/16 in b49 = 7/55
8,1,7 ← 8/17 in b64 = 8/71
9,1,8 ← 9/18 in b81 = 9/89
A,1,9 ← A/19 in b100 = 10/109 → 10,1,9
42,1,3 ← 4/213 in b8 = 4/139 → 34,1,3
4,1,2,3,3 ← 41/233 in b8 = 33/155
1,17,1,2,3 ← 117/123 in b14 = 217/227 → 1,21,1,2,3
3A,3 ← 3/A3 in b28 = 3/283 → 94,3
3,5,A,2 ← 35/A2 in b34 = 107/342 → 3,5,10,2
3,1,4,1,4,1,5 ← 314/1415 in b8 = 204/781
2,1,36,3,2 ← 213/632 in b12 = 303/902 → 2,1,42,3,2
3,2,11,2,2,2 ← 321/1222 in b9 = 262/911 → 3,2,10,2,2,2
4H,4 ← 4/H4 in b65 = 4/1109 → 277,4
6,2,1,3,J ← 62/13J in b35 = 212/1349 → 6,2,1,3,19
8,3,3,1,D ← 83/31D in b22 = 179/1487 → 8,3,3,1,13
93,1,8 ← 9/318 in b27 = 9/2222 → 246,1,8
1,3A,1,1,4,2,2 ← 13A1/1422 in b12 = 2281/2330 → 1,46,1,1,4,2,2
C7,1,B ← C/71B in b21 = 12/3119 → 259,1,11
1,2,2,1,O,F ← 122/1OF in b50 = 2602/3715 → 1,2,2,1,24,15
2,1,1,5,55 ← 211/555 in b28 = 1597/4065 → 2,1,1,5,145
3,1,1,A,K,6 ← 311/AK6 in b29 = 2553/8996 → 3,1,1,10,20,6
1,2[70],1,3,9 ← 12[70]/139 in b98 = 9870/9907 → 1,266,1,3,9
1,E,4,1,M,7 ← 1E4/1M7 in b100 = 11404/12207 → 1,14,4,1,22,7
LG,5,4 ← L/G54 in b28 = 21/12688 → 604,5,4
G4,1,F ← G/41F in b64 = 16/16463 → 1028,1,15

Back to Frac’

by in Arithmetic, Continued Fractions, Fractals, Mathematics and tagged , , , , , , , , , | Leave a comment

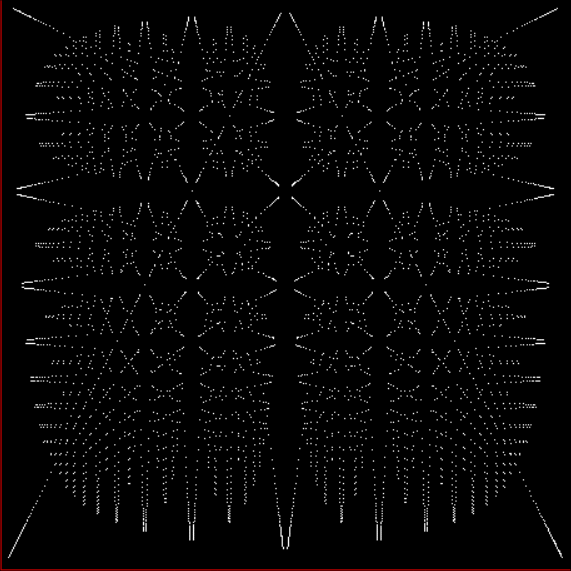
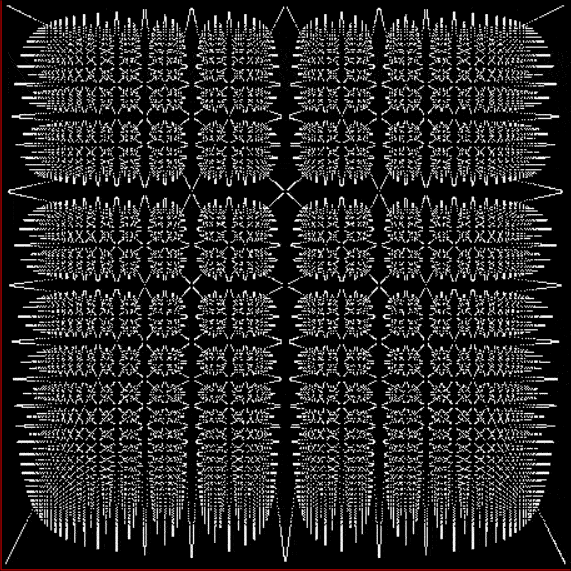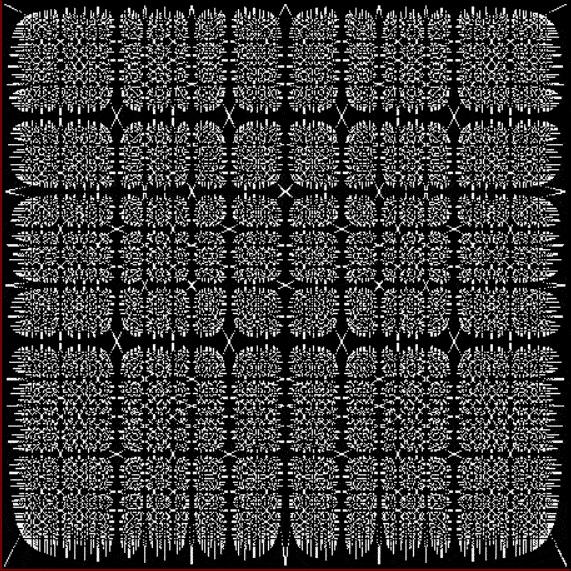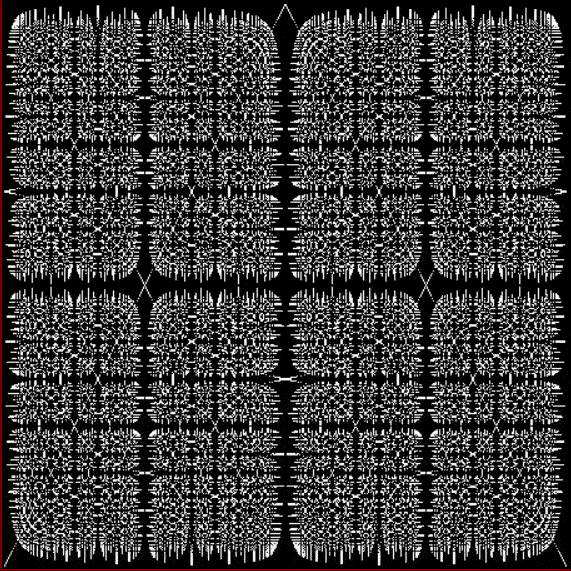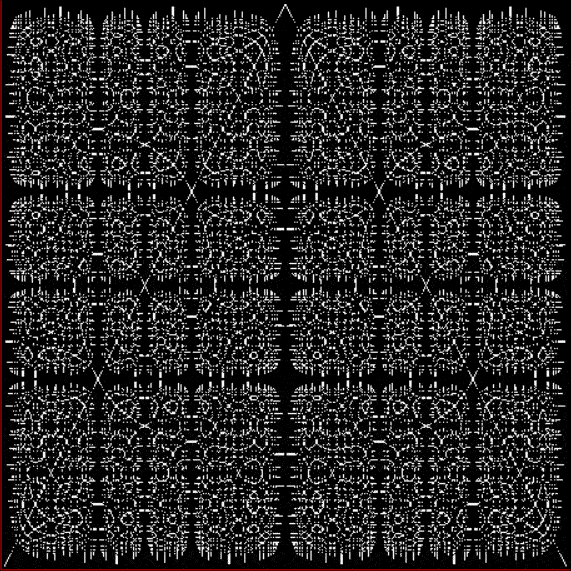
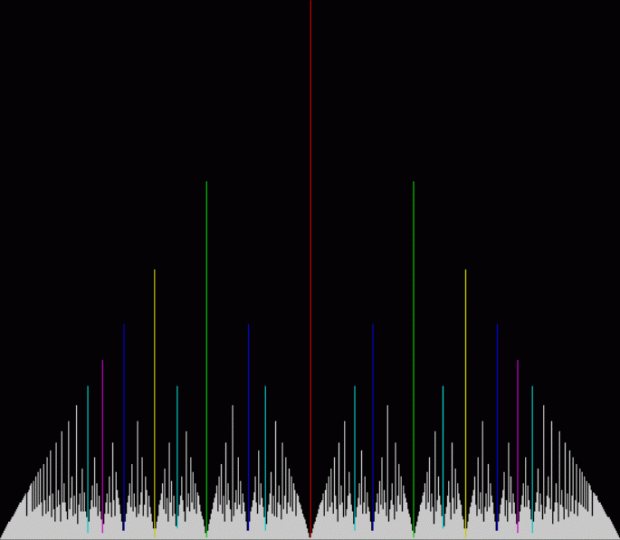
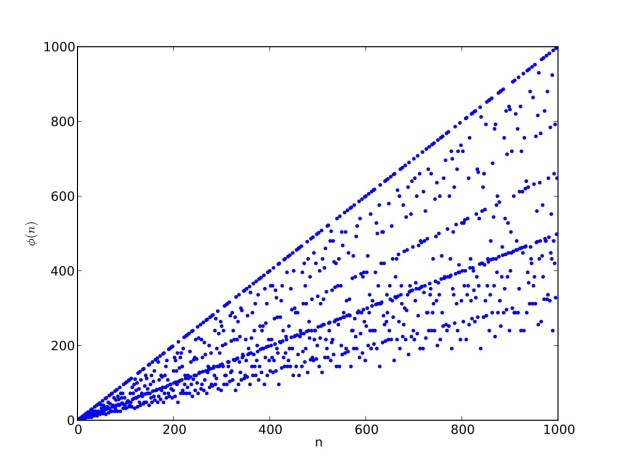
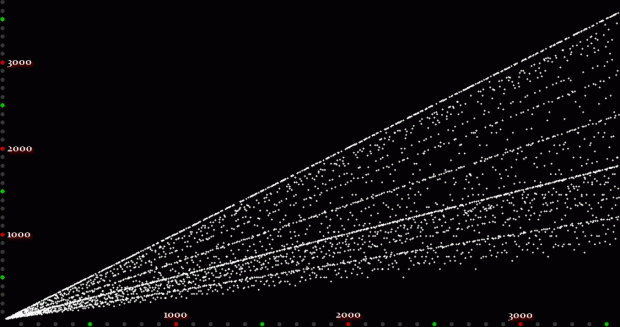
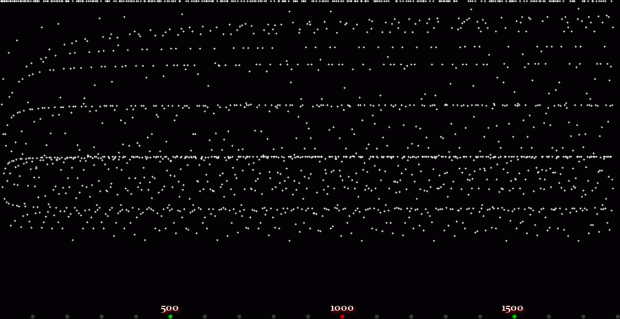
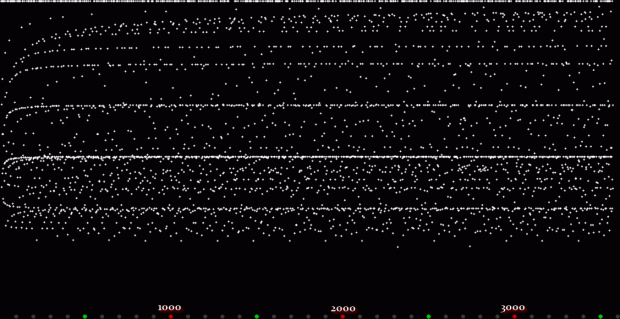
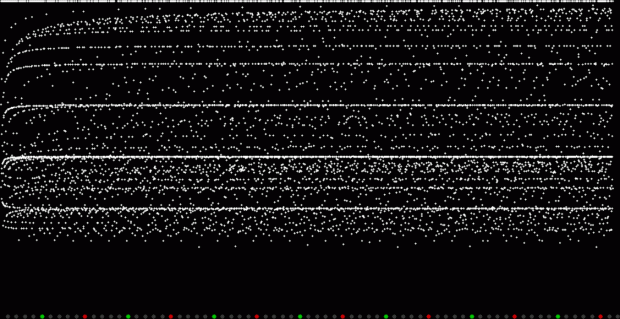
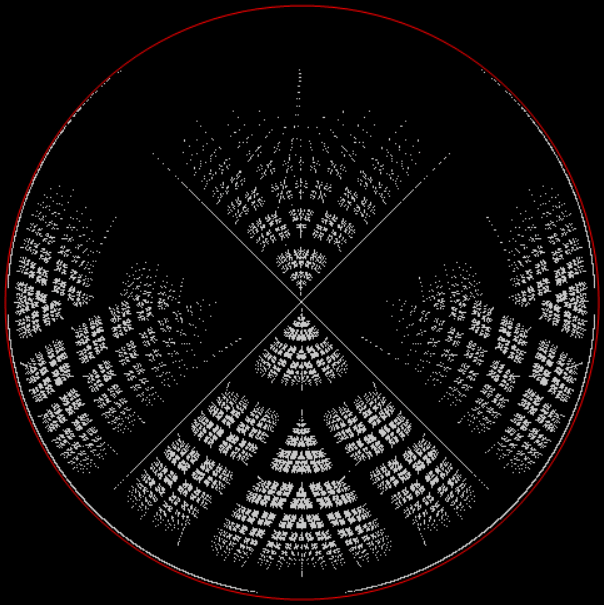
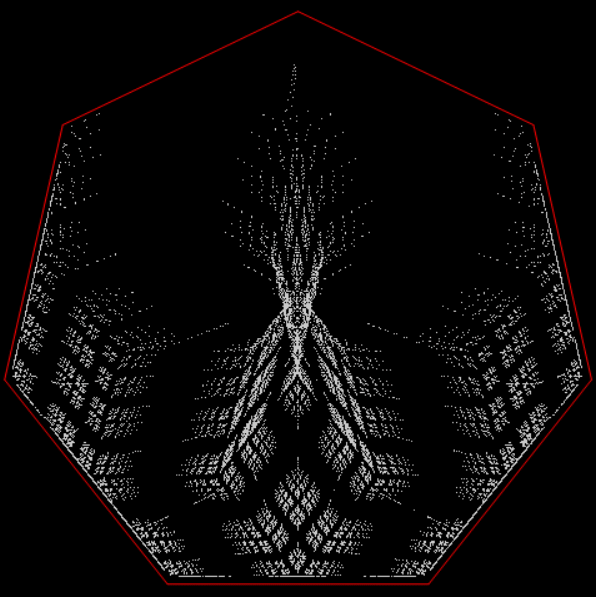
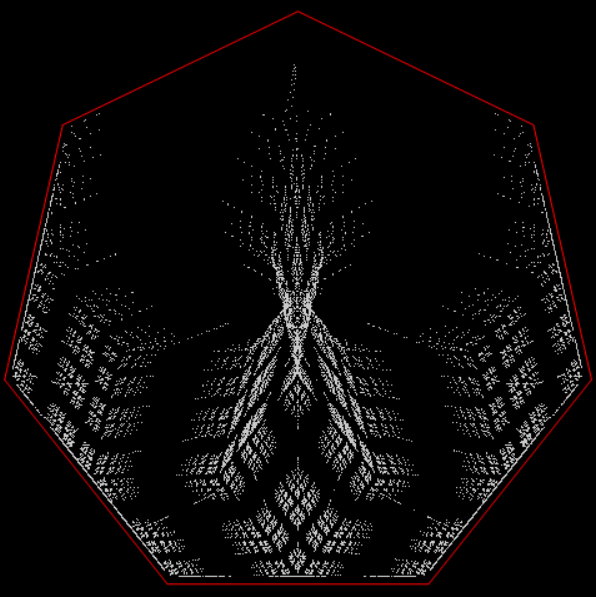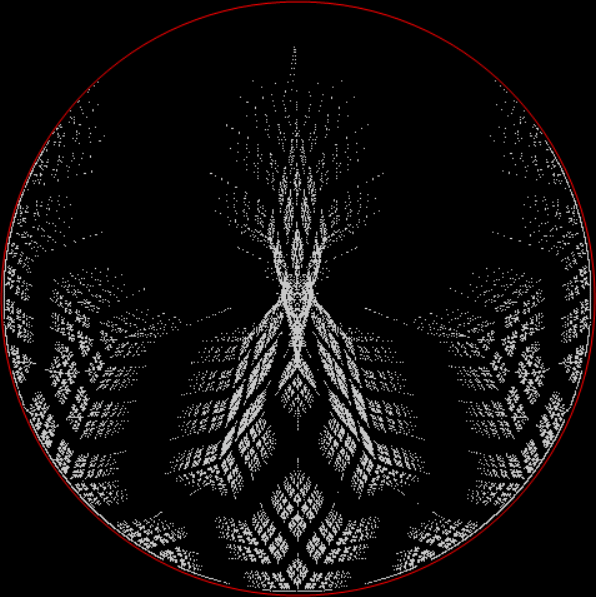
Here’s a second serendipitous fractal:

A serendipitous fractal on a fract-L

It looks like (and is related to) the limestone fractal and I found it similarly serendipitously. This time I was looking at continued fractions, a simple yet subtle and seductive way of representing non-integer numbers like 2/3 and 7/9 (or √2 and π). To generate a continued fraction from a/b < 1, you divide a/b into 1 and take away the integer part. Then you repeat with the remainder until nothing is left (or, as with irrationals like 1/√2 and 1/π, you've calculated long enough for your needs). The integers at each stage are the numbers of the continued fraction. Here is the working for contfrac(2/3), the continued fraction of 2/3:

int(1/(2/3)) = int(3/2) = int(1.5) = 1
3/2 – 1 = 1/2
int(1/(1/2)) = int(2) = 2
2 – 2 = 0

contfrac(2/3) = 1, 2

By working backwards with (1, 2), you can use the continued fraction to reconstruct the original number a/b. Start with a/b = 0/1:

1 / (0/1 + 2) = 1 / ((0+2*1)/2) = 1 / (2/1) = 1/2
1 / (1/2 + 1) = 1 / ((1+2*1)/2) = 1 / (3/2) = 2/3

And here’s the working for contfrac(7/9), the continued fraction of 7/9:

int(1/(7/9)) = int(9/7) = int(1.285714…) = 1
9/7 – 1 = 2/7
int(1/(2/7)) = int(7/2) = int(3.5) = 3
7/2 – 3 = 1/2
int(1/(1/2)) = int(2) = 2
2 – 2 = 0

contfrac(7/9) = 1, 3, 2

And here’s the reconstruction of 7/9 from its continued fraction, starting again with a/b = 0/1:

1 / (0/1 + 2) = 1 / ((0+2*1)/2) = 1 / (2/1) = 1/2
1 / (1/2 + 3) = 1 / ((1+2*3)/2) = 1 / (7/2) = 2/7
1 / (2/7 + 1) = 1 / ((2+7*1)/7) = 1 / (9/7) = 7/9

From that simple algorithm arise subtle and seductive things. Look at some continued fractions, cf(a/b), for a/b in simplest form (giving only the first few reciprocals, 1/b, because cf(1/b) = b). Interesting patterns appear, e.g. when a/b uses adjacent or nearly adjacent Fibonacci numbers:

cf(1/3) = 3 = cf(0.333333333…)
cf(2/3) = 1,2 = cf(0.666666666…)
cf(1/4) = 4 = cf(0.25)
cf(3/4) = 1,3 = cf(0.75)
cf(1/5) = 5 = cf(0.2)
cf(2/5) = 2,2 = cf(0.4)
cf(3/5) = 1,1,2 = cf(0.6)
cf(4/5) = 1,4 = cf(0.8)
cf(5/6) = 1,5 = cf(0.833333333…)
cf(2/7) = 3,2 = cf(0.285714285…)
cf(3/7) = 2,3 = cf(0.428571428…)
cf(4/7) = 1,1,3 = cf(0.571428571…)
cf(5/7) = 1,2,2 = cf(0.714285714…)
cf(6/7) = 1,6 = cf(0.857142857…)
cf(3/8) = 2,1,2 = cf(0.375)
cf(5/8) = 1,1,1,2 = cf(0.625)
cf(7/8) = 1,7 = cf(0.875)
cf(2/9) = 4,2 = cf(0.222222222…)
cf(4/9) = 2,4 = cf(0.444444444…)
cf(5/9) = 1,1,4 = cf(0.555555555…)
cf(7/9) = 1,3,2 = cf(0.777777777…)
cf(8/9) = 1,8 = cf(0.888888888…)
cf(3/10) = 3,3 = cf(0.3)
cf(7/10) = 1,2,3 = cf(0.7)
cf(9/10) = 1,9 = cf(0.9)
cf(2/11) = 5,2 = cf(0.181818181…)
cf(3/11) = 3,1,2 = cf(0.272727272…)
cf(4/11) = 2,1,3 = cf(0.363636363…)
cf(5/11) = 2,5 = cf(0.454545454…)
cf(6/11) = 1,1,5 = cf(0.545454545…)
cf(7/11) = 1,1,1,3 = cf(0.636363636…)
cf(8/11) = 1,2,1,2 = cf(0.727272727…)
cf(9/11) = 1,4,2 = cf(0.818181818…)
cf(10/11) = 1,10 = cf(0.909090909…)
cf(5/12) = 2,2,2 = cf(0.416666666…)
cf(7/12) = 1,1,2,2 = cf(0.583333333…)
cf(11/12) = 1,11 = cf(0.916666666…)
cf(2/13) = 6,2 = cf(0.153846153…)
cf(3/13) = 4,3 = cf(0.230769230…)
cf(4/13) = 3,4 = cf(0.307692307…)
cf(5/13) = 2,1,1,2 = cf(0.384615384…)
cf(6/13) = 2,6 = cf(0.461538461…)
cf(7/13) = 1,1,6 = cf(0.538461538…)
cf(8/13) = 1,1,1,1,2 = cf(0.615384615…)
cf(9/13) = 1,2,4 = cf(0.692307692…)
cf(10/13) = 1,3,3 = cf(0.769230769…)
cf(11/13) = 1,5,2 = cf(0.846153846…)
cf(12/13) = 1,12 = cf(0.923076923…)
cf(3/14) = 4,1,2 = cf(0.214285714…)
cf(5/14) = 2,1,4 = cf(0.357142857…)
cf(9/14) = 1,1,1,4 = cf(0.642857142…)
cf(11/14) = 1,3,1,2 = cf(0.785714285…)
cf(13/14) = 1,13 = cf(0.928571428…)
cf(2/15) = 7,2 = cf(0.133333333…)
cf(4/15) = 3,1,3 = cf(0.266666666…)
cf(7/15) = 2,7 = cf(0.466666666…)
cf(8/15) = 1,1,7 = cf(0.533333333…)
cf(11/15) = 1,2,1,3 = cf(0.733333333…)
cf(13/15) = 1,6,2 = cf(0.866666666…)
cf(14/15) = 1,14 = cf(0.933333333…)
cf(3/16) = 5,3 = cf(0.1875)
cf(5/16) = 3,5 = cf(0.3125)
cf(7/16) = 2,3,2 = cf(0.4375)

After investigating some of those patterns, I wondered what happened when you reversed the continued fraction cf(a/b) and used those reversed numbers backward (that is, used the numbers of cf(a/b) forward) to generate another and different a/b. And a/b will always be different unless cf(a/b) is a palindrome, like cf(5/12) = 2,2,2 or cf(5/13) = 2,1,1,2 or cf(4/15) = 3,1,3. Note that a continued fraction never ends in 1, so that when reversing, say, cf(5/8) = (1, 1, 1, 2), you need an adjustment from (2, 1, 1, 1) to (2, 1, 1+1) = (2, 1, 2). Here’s a little of what happens when you reverse cf(a1/b1) to generate a2/b2:

cf(1/2) = 2 → 2 = cf(1/2)
1/2 = 0.5 : 0.5 = 1/2
cf(1/3) = 3 → 3 = cf(1/3)
1/3 = 0.333333333 : 0.333333333 = 1/3
cf(2/3) = 1, 2 → 2, 1 → 3 = cf(1/3)
2/3 = 0.666666666 : 0.333333333 = 1/3
cf(3/4) = 1, 3 → 3, 1 → 4 = cf(1/4)
3/4 = 0.75 : 0.25 = 1/4
cf(2/5) = 2, 2 → 2, 2 = cf(2/5)
2/5 = 0.4 : 0.4 = 2/5
cf(3/5) = 1, 1, 2 → 2, 1, 1 → 2, 2 = cf(2/5)
3/5 = 0.6 : 0.4 = 2/5
cf(4/5) = 1, 4 → 4, 1 → 5 = cf(1/5)
4/5 = 0.8 : 0.2 = 1/5
cf(5/6) = 1, 5 → 5, 1 → 6 = cf(1/6)
5/6 = 0.833333333 : 0.166666666 = 1/6
cf(2/7) = 3, 2 → 2, 3 = cf(3/7)
2/7 = 0.285714286 : 0.428571428 = 3/7
cf(3/7) = 2, 3 → 3, 2 = cf(2/7)
3/7 = 0.428571429 : 0.285714286 = 2/7
cf(4/7) = 1, 1, 3 → 3, 1, 1 → 3, 2 = cf(2/7)
4/7 = 0.571428571 : 0.285714286 = 2/7
cf(5/7) = 1, 2, 2 → 2, 2, 1 → 2, 3 = cf(3/7)
5/7 = 0.714285714 : 0.428571429 = 3/7
cf(6/7) = 1, 6 → 6, 1 → 7 = cf(1/7)
6/7 = 0.857142857 : 0.142857143 = 1/7
cf(3/8) = 2, 1, 2 → 2, 1, 2 = cf(3/8)
0.375 : 0.375
cf(5/8) = 1, 1, 1, 2 → 2, 1, 1, 1 → 2, 1, 2 = cf(3/8)
0.625 : 0.375
cf(7/8) = 1, 7 → 7, 1 → 8 = cf(1/8)
0.875 : 0.125
cf(2/9) = 4, 2 → 2, 4 = cf(4/9)
0.222222222 : 0.444444444
cf(4/9) = 2, 4 → 4, 2 = cf(2/9)
0.444444444 : 0.222222222

And if you plot x = a1/b1 and y = (a2/b2 * 2) on a fract-L, that is, a graph whose horizontal and vertical arms represent 0 to 1, you get the fractal right at the beginning:

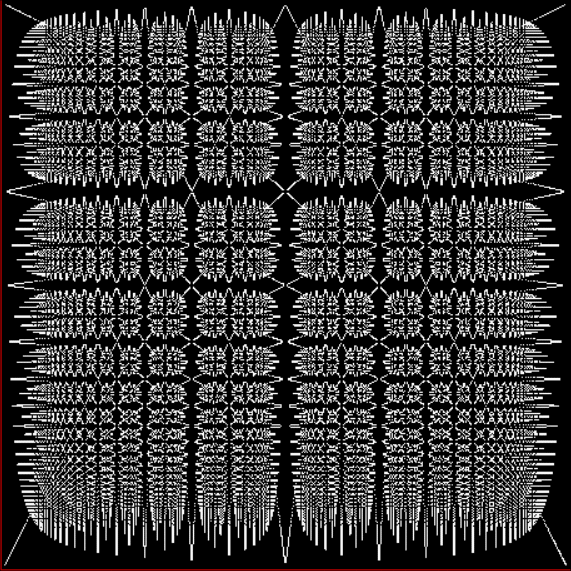
Fract-L for x = a1/b1 and y = (a2/b2 * 2), where a2/b2 is generated from reversed(cf(a1/b1))

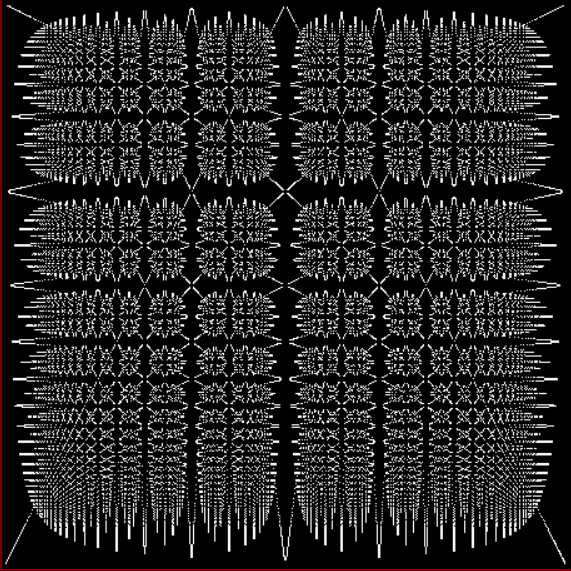
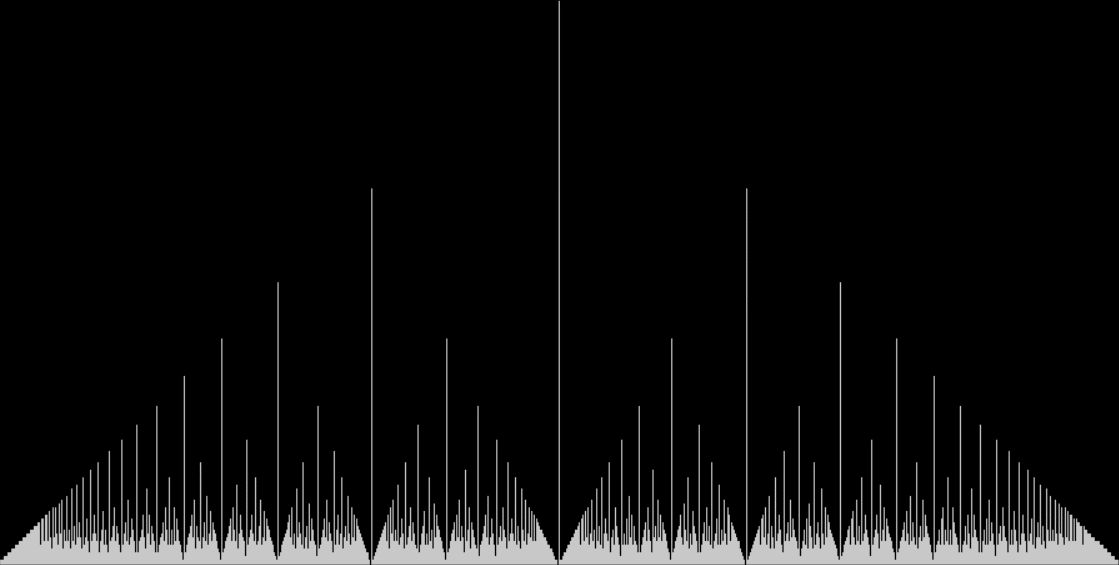
You need to use (a2/b2 * 2) because a2/b2 from reversed(cf(a1/b1)) is always <= 0.5, so using raw a2/b2 generates this graph:

Fract-L for x = a1/b1 and y = a2/b2 (i.e. a2/b2 is unadjusted)

Why is it always true that a2/b2 <= 0.5? For two reasons. First, a/b > 0.5 always generate continued fractions that start with 1, like cf(2/3) = 1, 2 or cf(3/4) = 1, 3 or cf(3/5) = 1, 1, 2. Second, as previously mentioned, no continued fraction ends with 1. Therefore a reversed cf(a1/b1), where the final number, n > 1, moves to the beginning, will never begin with 1 and the a2/b2 generated from reversed(cf(a1/b1)) will always be less than 0.5 (or equal to it in the solitary case of cf(1/2) = 2).

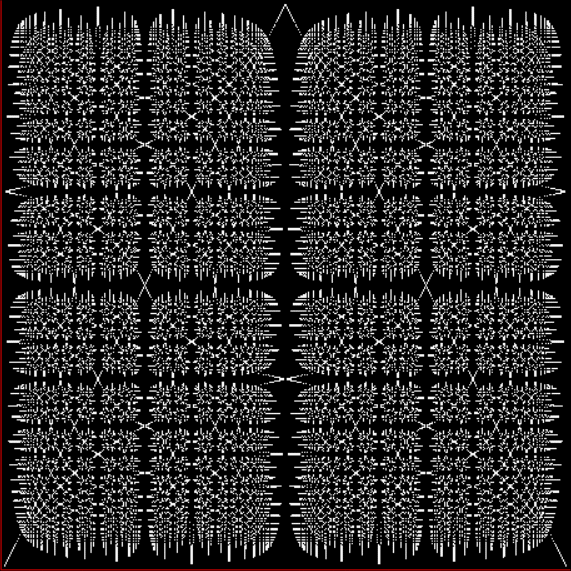
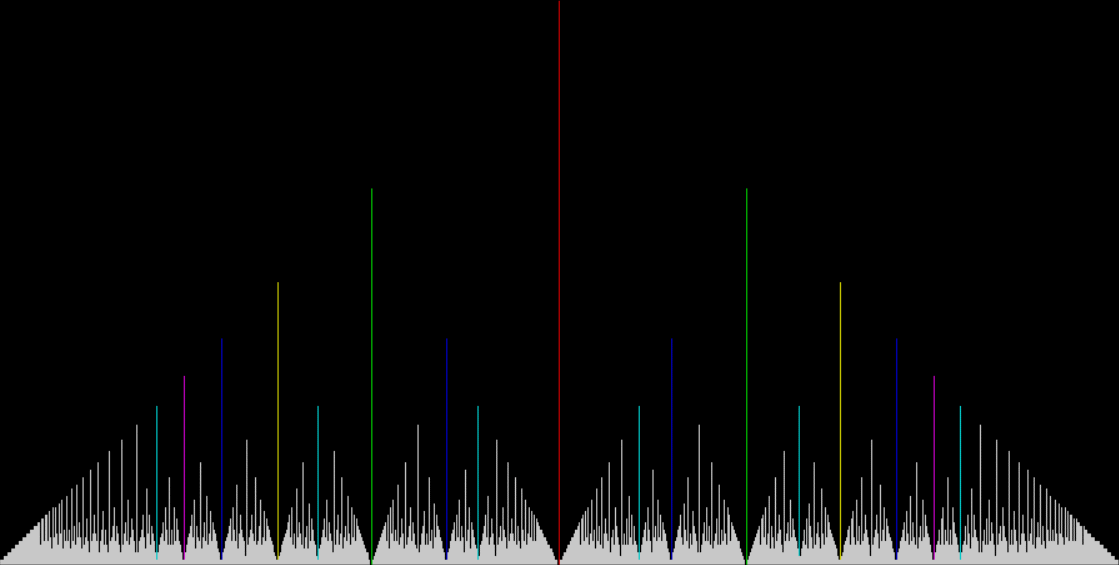
Now let's look at the development of the fractal as a1/b1 uses larger and larger denominators:

Fract-L for x = a1/b1 and y = (a2/b2 * 2) for a1/b1 <= 6/7

Fract-L for for a1/b1 <= 14/15

Fract-L for a1/b1 <= 30/31

Fract-L for a1/b1 <= 62/63

Fract-L for a1/b1 <= 126/127

Fract-L for a1/b1 <= 254/255

Fract-L for a1/b1 <= 357/358

Fract-L for a1/b1 <= 467/468

Animated fract-L for x = a1/b1 and y = (a2/b2 * 2) (animated at ezGif)

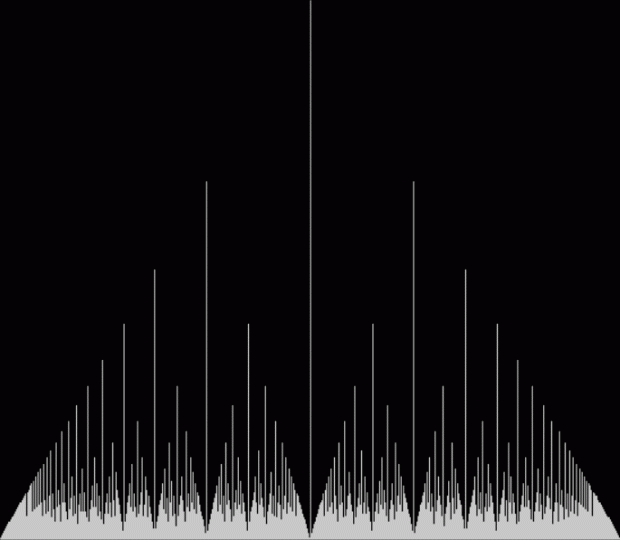
The fractal changes subtly when you restrict the b1 of a1/b1 in some way, say using multiples of 2, 3, 4, 5…:

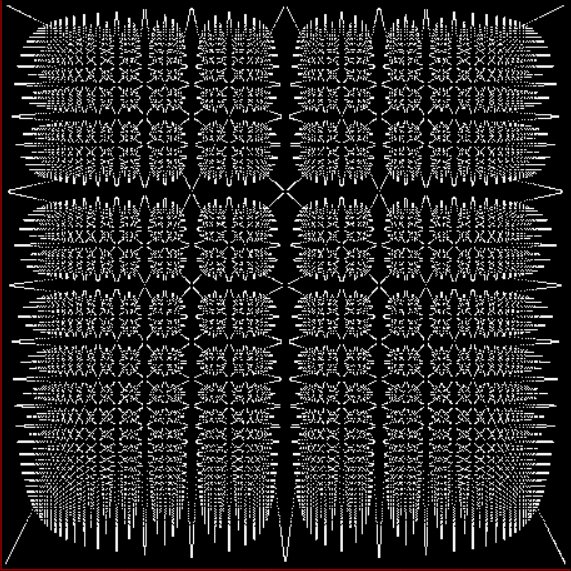
Fract-L for x = a1/b1 and y = (a2/b2 * 2) for b1 = n = 2, 3, 4, 5, 6, 7, 8…

Fract-L for b1 = 2n = 2, 4, 6, 8, 10…

Fract-L for b1 = 3n = 3, 6, 9, 12, 15…

Fract-L for b1 = 4n

Fract-L for b1 = 5n

Fract-L for b1 = 6n

Animated fract-L for b1 = 1n..12n (animated at ezGif)

Finally, here are fract-Ls when b1 is a triangular, square, hexagonal or octagonal number:

Fract-L for x = a1/b1 and y = (a2/b2 * 2) for triangular(b1) = 3, 6, 10, 15, 21, 28,…

Fract-L for square(b1) = 4, 9, 16, 25, 36, 49,…

Fract-L for hexagonal(b1) = 6, 15, 28, 45, 66, 91,…

Fract-L for octagonal(b1) = 8, 21, 40, 65, 96, 133,…

Elsewhere Other-Accessible…

• Back to Drac’ — a parallel pun for a pre-previous fractal
• I Like Gryke — a first look at the limestone fractal
• Lime Time — more on the limestone fractal

Fractional Fractal

by in Arithmetic, Fractals, Geometry, Mathematics | Leave a comment

Serendipity in some simplification statistics. That’s what I encountered the other day. I was looking at the ways to simplify this set of fractions:

1/2, 1/3, 2/3, 1/4, 2/4, 3/4, 1/5, 2/5, 3/5, 4/5, 1/6, 2/6, 3/6, 4/6, 5/6, 1/7, 2/7, 3/7, 4/7, 5/7, 6/7, 1/8, 2/8, 3/8, 4/8, 5/8, 6/8, 7/8, 1/9, 2/9, 3/9, 4/9, 5/9, 6/9, 7/9, 8/9, 1/10, 2/10, 3/10, 4/10, 5/10, 6/10, 7/10, 8/10, 9/10, 1/11, 2/11, 3/11, …

The underlined fractions are not in their simplest possible form. For example, 2/4 simplifies to 1/2, 2/6 to 1/3, 3/6 to 1/2, and so on:

1/2, 1/3, 2/3, 1/4, 2/4 → 1/2, 3/4, 1/5, 2/5, 3/5, 4/5, 1/6, 2/6 → 1/3, 3/6 → 1/2, 4/6 → 2/3, 5/6, 1/7, 2/7, 3/7, 4/7, 5/7, 6/7, 1/8, 2/8 → 1/4, 3/8, 4/8 → 1/2, 5/8, 6/8 → 3/4, 7/8, 1/9, 2/9, 3/9 → 1/3, 4/9, 5/9, 6/9 → 2/3, 7/9, 8/9, 1/10, 2/10 → 1/5, 3/10, 4/10 → 2/5, 5/10 → 1/2, 6/10 → 3/5, 7/10, 8/10 → 4/5, 9/10, 1/11, 2/11, 3/11, …

I counted the number of times the simplest possible fractions occurred when simplifying all fractions a/b for (b = 2..n, a = 1..b-1), then displayed the stats as a graph running from 0/1 to 1/1. And there was serendipity in these simplification statistics, because a fractal had appeared:

Graph for count of simplest possible fractions from a/b for (b = 2..n, a = 1..b-1)

It’s interesting to work out what fractions appear where. For example, the peak in the middle is 1/2, but what are the next-highest peaks on either side? The answers are more obvious in the colored version of the graph:

Colored graph for count of simplest possible fractions
Key: n/2, n/3, n/4, n/5, n/6, n/7

The line for 1/2 is red, the lines for 1/3 and 2/3 in light green, the lines for 1/4 and 3/4 in yellow, and so on. But those graphs appear in an equilateral triangle, as it were. The fractals get easier to see in the full-sized versions of these widened graphs:

Widened graph for count of simplest possible fractions from a/b for (b = 2..n, a = 1..b-1)

(click for full size)

Widened and colored graph for count of simplest possible fractions

(click for full size)

Powers of Persistence

by in Arithmetic, Base Behavior, Mathematics and tagged , | Leave a comment

“The persistence of a number is the number of times you need to multiply the digits together before reaching a single digit.” — OEIS

Base 5

23 → 11 → 1 in b5 (c=3) (n=13 in b10)
233 → 33 → 14 → 4 in b5 (c=4) (n=68 in b10)
33334 → 2244 → 224 → 31 → 3 in b5 (c=5) (n=2344 in b10)
444444444444 → 13243332331 → 333124 → 1331 → 14 → 4 in b5 (c=6) (n=244140624 in b10)
3344444444444444444444 → 2244112144242244414 → 13243332331 → 333124 → 1331 → 14 → 4 in b5 (c=7) (n=1811981201171874 in b10)

Base 6

23 → 10 → 0 in b6 (c=3) (n=15 in b10)
35 → 23 → 10 → 0 in b6 (c=4) (n=23 in b10)
444 → 144 → 24 → 12 → 2 in b6 (c=5) (n=172 in b10)
24445 → 2544 → 424 → 52 → 14 → 4 in b6 (c=6) (n=3629 in b10)

Base 7

24 → 11 → 1 in b7 (c=3) (n=18 in b10)
36 → 24 → 11 → 1 in b7 (c=4) (n=27 in b10)
245 → 55 → 34 → 15 → 5 in b7 (c=5) (n=131 in b10)
4445 → 635 → 156 → 42 → 11 → 1 in b7 (c=6) (n=1601 in b10)
44556 → 6666 → 3531 → 63 → 24 → 11 → 1 in b7 (c=7) (n=11262 in b10)
5555555 → 443525 → 6666 → 3531 → 63 → 24 → 11 → 1 in b7 (c=8) (n=686285 in b10)
444555555555555666 → 465556434443526 → 115443241155 → 256641 → 4125 → 55 → 34 → 15 → 5 in b7 (c=9) (n=1086400325525346 in b10)

Base 8

24 → 10 → 0 in b8 (c=3) (n=20 in b10)
37 → 25 → 12 → 2 in b8 (c=4) (n=31 in b10)
256 → 74 → 34 → 14 → 4 in b8 (c=5) (n=174 in b10)
2777 → 1256 → 74 → 34 → 14 → 4 in b8 (c=6) (n=1535 in b10)
333555577 → 3116773 → 5126 → 74 → 34 → 14 → 4 in b8 (c=7) (n=57596799 in b10)

Base 9

25 → 11 → 1 in b9 (c=3) (n=23 in b10)
38 → 26 → 13 → 3 in b9 (c=4) (n=35 in b10)
57 → 38 → 26 → 13 → 3 in b9 (c=5) (n=52 in b10)
477 → 237 → 46 → 26 → 13 → 3 in b9 (c=6) (n=394 in b10)
45788 → 13255 → 176 → 46 → 26 → 13 → 3 in b9 (c=7) (n=30536 in b10)
2577777 → 275484 → 13255 → 176 → 46 → 26 → 13 → 3 in b9 (c=8) (n=1409794 in b10)

Base 10

25 → 10 → 0 (c=3)
39 → 27 → 14 → 4 (c=4)
77 → 49 → 36 → 18 → 8 (c=5)
679 → 378 → 168 → 48 → 32 → 6 (c=6)
6788 → 2688 → 768 → 336 → 54 → 20 → 0 (c=7)
68889 → 27648 → 2688 → 768 → 336 → 54 → 20 → 0 (c=8)
2677889 → 338688 → 27648 → 2688 → 768 → 336 → 54 → 20 → 0 (c=9)
26888999 → 4478976 → 338688 → 27648 → 2688 → 768 → 336 → 54 → 20 → 0 (c=10)
3778888999 → 438939648 → 4478976 → 338688 → 27648 → 2688 → 768 → 336 → 54 → 20 → 0 (c=11)
277777788888899 → 4996238671872 → 438939648 → 4478976 → 338688 → 27648 → 2688 → 768 → 336 → 54 → 20 → 0 (c=12)

Base 11

26 → 11 → 1 in b11 (c=3) (n=28 in b10)
3A → 28 → 15 → 5 in b11 (c=4) (n=43 in b10)
69 → 4A → 37 → 1A → A in b11 (c=5) (n=75 in b10)
269 → 99 → 74 → 26 → 11 → 1 in b11 (c=6) (n=317 in b10)
3579 → 78A → 46A → 1A9 → 82 → 15 → 5 in b11 (c=7) (n=4684 in b10)
26778 → 3597 → 78A → 46A → 1A9 → 82 → 15 → 5 in b11 (c=8) (n=38200 in b10)
47788A → 86277 → 3597 → 78A → 46A → 1A9 → 82 → 15 → 5 in b11 (c=9) (n=757074 in b10)
67899AAA → 143A9869 → 299596 → 2A954 → 2783 → 286 → 88 → 59 → 41 → 4 in b11 (c=10) (n=130757439 in b10)
77777889999 → 2AA174996A → 143A9869 → 299596 → 2A954 → 2783 → 286 → 88 → 59 → 41 → 4 in b11 (c=11) (n=199718348047 in b10)

Base 12

26 → 10 → 0 in b12 (c=3) (n=30 in b10)
3A → 26 → 10 → 0 in b12 (c=4) (n=46 in b10)
6B → 56 → 26 → 10 → 0 in b12 (c=5) (n=83 in b10)
777 → 247 → 48 → 28 → 14 → 4 in b12 (c=6) (n=1099 in b10)
AAB → 778 → 288 → A8 → 68 → 40 → 0 in b12 (c=7) (n=1571 in b10)
3577777799 → 3BA55B53 → 557916 → 5576 → 736 → A6 → 50 → 0 in b12 (c=8) (n=17902874277 in b10)

Base 13

27 → 11 → 1 in b13 (c=3) (n=33 in b10)
3B → 27 → 11 → 1 in b13 (c=4) (n=50 in b10)
5A → 3B → 27 → 11 → 1 in b13 (c=5) (n=75 in b10)
9A → 6C → 57 → 29 → 15 → 5 in b13 (c=6) (n=127 in b10)
27A → AA → 79 → 4B → 35 → 12 → 2 in b13 (c=7) (n=439 in b10)
8AC → 58B → 27B → BB → 94 → 2A → 17 → 7 in b13 (c=8) (n=1494 in b10)
35AB → 99C → 59A → 288 → 9B → 78 → 44 → 13 → 3 in b13 (c=9) (n=7577 in b10)
9BBB → 55B6 → 99C → 59A → 288 → 9B → 78 → 44 → 13 → 3 in b13 (c=10) (n=21786 in b10)
2999BBC → 591795 → 65B5 → 99C → 59A → 288 → 9B → 78 → 44 → 13 → 3 in b13 (c=11) (n=13274091 in b10)
28CCCCCC → 9B89B93 → 591795 → 65B5 → 99C → 59A → 288 → 9B → 78 → 44 → 13 → 3 in b13 (c=12) (n=168938314 in b10)
377AAAABCCC → 2833B38BCB → B588A8A → 777995 → 4B2CA → 4A64 → 58B → 27B → BB → 94 → 2A → 17 → 7 in b13 (c=13) (n=494196864368 in b10)

Base 14

27 → 10 → 0 in b14 (c=3) (n=35 in b10)
3C → 28 → 12 → 2 in b14 (c=4) (n=54 in b10)
5B → 3D → 2B → 18 → 8 in b14 (c=5) (n=81 in b10)
99 → 5B → 3D → 2B → 18 → 8 in b14 (c=6) (n=135 in b10)
359 → 99 → 5B → 3D → 2B → 18 → 8 in b14 (c=7) (n=667 in b10)
CCC → 8B6 → 29A → CC → A4 → 2C → 1A → A in b14 (c=8) (n=2532 in b10)
359AB → 55AA → CA8 → 4C8 → 1D6 → 58 → 2C → 1A → A in b14 (c=9) (n=130883 in b10)
CDDDD → 8CC8C → 2C436 → 8B6 → 29A → CC → A4 → 2C → 1A → A in b14 (c=10) (n=499407 in b10)
3ABBDDDD → DAAAD54 → 63DAC8 → 5BC1A → 2596 → 2A8 → B6 → 4A → 2C → 1A → A in b14 (c=11) (n=397912927 in b10)
488AABCCCDDD → 39A59889584 → A89DBD84 → 598D14C → 5BC1A → 2596 → 2A8 → B6 → 4A → 2C → 1A → A in b14 (c=12) (n=18693488093783 in b10)

Base 15

28 → 11 → 1 in b15 (c=3) (n=38 in b10)
3D → 29 → 13 → 3 in b15 (c=4) (n=58 in b10)
5E → 4A → 2A → 15 → 5 in b15 (c=5) (n=89 in b10)
28C → CC → 99 → 56 → 20 → 0 in b15 (c=6) (n=582 in b10)
8AE → 4EA → 275 → 4A → 2A → 15 → 5 in b15 (c=7) (n=1964 in b10)
5BBB → 1E8A → 4EA → 275 → 4A → 2A → 15 → 5 in b15 (c=8) (n=19526 in b10)
BBBCC → 3BBC9 → B939 → BD3 → 1D9 → 7C → 59 → 30 → 0 in b15 (c=9) (n=596667 in b10)
2999BDE → 3C9CE6 → 66B7C → 9CC9 → 36C9 → 899 → 2D3 → 53 → 10 → 0 in b15 (c=10) (n=30104309 in b10)
39BBCCCCCD → 41CBD6D4C → 23C96E6 → 66B7C → 9CC9 → 36C9 → 899 → 2D3 → 53 → 10 → 0 in b15 (c=11) (n=140410607143 in b10)

Base 16

28 → 10 → 0 in b16 (c=3) (n=40 in b10)
3E → 2A → 14 → 4 in b16 (c=4) (n=62 in b10)
5F → 4B → 2C → 18 → 8 in b16 (c=5) (n=95 in b10)
BB → 79 → 3F → 2D → 1A → A in b16 (c=6) (n=187 in b10)
2AB → DC → 9C → 6C → 48 → 20 → 0 in b16 (c=7) (n=683 in b10)
3DDE → 1BBA → 4BA → 1B8 → 58 → 28 → 10 → 0 in b16 (c=8) (n=15838 in b10)
379BDD → 55C77 → 396C → 798 → 1F8 → 78 → 38 → 18 → 8 in b16 (c=9) (n=3644381 in b10)

Base 17

29 → 11 → 1 in b17 (c=3) (n=43 in b10)
3F → 2B → 15 → 5 in b17 (c=4) (n=66 in b10)
5G → 4C → 2E → 1B → B in b17 (c=5) (n=101 in b10)
9F → 7G → 6A → 39 → 1A → A in b17 (c=6) (n=168 in b10)
CE → 9F → 7G → 6A → 39 → 1A → A in b17 (c=7) (n=218 in b10)
3DD → 1CE → 9F → 7G → 6A → 39 → 1A → A in b17 (c=8) (n=1101 in b10)
9CF → 5A5 → EC → 9F → 7G → 6A → 39 → 1A → A in b17 (c=9) (n=2820 in b10)
2AFF → F9C → 5A5 → EC → 9F → 7G → 6A → 39 → 1A → A in b17 (c=10) (n=12986 in b10)
55DDF → CF4G → 25EB → 55A → EC → 9F → 7G → 6A → 39 → 1A → A in b17 (c=11) (n=446163 in b10)
39DDGG → DGCG7 → 35F54 → F9C → 5A5 → EC → 9F → 7G → 6A → 39 → 1A → A in b17 (c=12) (n=5079174 in b10)
DEGGGG → 86DCDC → DGCG7 → 35F54 → F9C → 5A5 → EC → 9F → 7G → 6A → 39 → 1A → A in b17 (c=13) (n=19710955 in b10)
6BBBBBEEF → 6FBEB7G8 → 5B39ACE → 1CED8G → 35F54 → F9C → 5A5 → EC → 9F → 7G → 6A → 39 → 1A → A in b17 (c=14) (n=46650378808 in b10)
2BDDDDDEEEEEF → 1FBBBB76B714 → 6FBEB7G8 → 5B39ACE → 1CED8G → 35F54 → F9C → 5A5 → EC → 9F → 7G → 6A → 39 → 1A → A in b17 (c=15) (n=1570081251102035 in b10)

Base 18

29 → 10 → 0 in b18 (c=3) (n=45 in b10)
3F → 29 → 10 → 0 in b18 (c=4) (n=69 in b10)
5E → 3G → 2C → 16 → 6 in b18 (c=5) (n=104 in b10)
8D → 5E → 3G → 2C → 16 → 6 in b18 (c=6) (n=157 in b10)
2BB → D8 → 5E → 3G → 2C → 16 → 6 in b18 (c=7) (n=857 in b10)
2CEG → GAC → 5GC → 2H6 → B6 → 3C → 20 → 0 in b18 (c=8) (n=15820 in b10)
AABF → 2EGC → GAC → 5GC → 2H6 → B6 → 3C → 20 → 0 in b18 (c=9) (n=61773 in b10)
8GGHH → 5B8DE → DD2G → GC8 → 4D6 → H6 → 5C → 36 → 10 → 0 in b18 (c=10) (n=938627 in b10)
AAAAAAH → 8HGH28 → 5B8DE → DD2G → GC8 → 4D6 → H6 → 5C → 36 → 10 → 0 in b18 (c=11) (n=360129437 in b10)

Base 19

2A → 11 → 1 in b19 (c=3) (n=48 in b10)
3G → 2A → 11 → 1 in b19 (c=4) (n=73 in b10)
5F → 3I → 2G → 1D → D in b19 (c=5) (n=110 in b10)
AB → 5F → 3I → 2G → 1D → D in b19 (c=6) (n=201 in b10)
DH → BC → 6I → 5D → 38 → 15 → 5 in b19 (c=7) (n=264 in b10)
2BC → DH → BC → 6I → 5D → 38 → 15 → 5 in b19 (c=8) (n=943 in b10)
7BG → 37G → HD → BC → 6I → 5D → 38 → 15 → 5 in b19 (c=9) (n=2752 in b10)
DII → BCD → 4E6 → HD → BC → 6I → 5D → 38 → 15 → 5 in b19 (c=10) (n=5053 in b10)
4AAH → IFH → CDB → 4E6 → HD → BC → 6I → 5D → 38 → 15 → 5 in b19 (c=11) (n=31253 in b10)
3BGII → 15HGF → 2I9D → BCD → 4E6 → HD → BC → 6I → 5D → 38 → 15 → 5 in b19 (c=12) (n=472548 in b10)
EEFHH → 69GBI → 15HGF → 2I9D → BCD → 4E6 → HD → BC → 6I → 5D → 38 → 15 → 5 in b19 (c=13) (n=1926275 in b10)
ADEFFH → 2F7HHE → 69GBI → 15HGF → 2I9D → BCD → 4E6 → HD → BC → 6I → 5D → 38 → 15 → 5 in b19 (c=14) (n=26556906 in b10)
4ADDDDEEF → 3E7919IH → 2HH7FE → 69GBI → 15HGF → 2I9D → BCD → 4E6 → HD → BC → 6I → 5D → 38 → 15 → 5 in b19 (c=15) (n=77518543969 in b10)
9999999BBFHHHI → 6B41DG4CB3BG → H27A5F3D → 2F7HHE → 69GBI → 15HGF → 2I9D → BCD → 4E6 → HD → BC → 6I → 5D → 38 → 15 → 5 in b19 (c=16) (n=399503342991325867 in b10)

Base 20

2A → 10 → 0 in b20 (c=3) (n=50 in b10)
3H → 2B → 12 → 2 in b20 (c=4) (n=77 in b10)
6D → 3I → 2E → 18 → 8 in b20 (c=5) (n=133 in b10)
7J → 6D → 3I → 2E → 18 → 8 in b20 (c=6) (n=159 in b10)
DI → BE → 7E → 4I → 3C → 1G → G in b20 (c=7) (n=278 in b10)
6DE → 2EC → GG → CG → 9C → 58 → 20 → 0 in b20 (c=8) (n=2674 in b10)
CGG → 7DC → 2EC → GG → CG → 9C → 58 → 20 → 0 in b20 (c=9) (n=5136 in b10)
2BHI → GGC → 7DC → 2EC → GG → CG → 9C → 58 → 20 → 0 in b20 (c=10) (n=20758 in b10)
CDGG → 4JGG → 28CG → 7DC → 2EC → GG → CG → 9C → 58 → 20 → 0 in b20 (c=11) (n=101536 in b10)
2DEGJ → DGCG → 4JGG → 28CG → 7DC → 2EC → GG → CG → 9C → 58 → 20 → 0 in b20 (c=12) (n=429939 in b10)
77BBHJ → BJ7D7 → GCGD → 4JGG → 28CG → 7DC → 2EC → GG → CG → 9C → 58 → 20 → 0 in b20 (c=13) (n=23612759 in b10)
BBBCEEHHHHH → 8DCB4G21J4 → 21ED4J4 → DGCG → 4JGG → 28CG → 7DC → 2EC → GG → CG → 9C → 58 → 20 → 0 in b20 (c=14) (n=118569903663157 in b10)

Base 21

2B → 11 → 1 in b21 (c=3) (n=53 in b10)
3I → 2C → 13 → 3 in b21 (c=4) (n=81 in b10)
6H → 4I → 39 → 16 → 6 in b21 (c=5) (n=143 in b10)
AK → 9B → 4F → 2I → 1F → F in b21 (c=6) (n=230 in b10)
GH → CK → B9 → 4F → 2I → 1F → F in b21 (c=7) (n=353 in b10)
4GI → 2CI → KC → B9 → 4F → 2I → 1F → F in b21 (c=8) (n=2118 in b10)
GII → BFI → 6F9 → 1HC → 9F → 69 → 2C → 13 → 3 in b21 (c=9) (n=7452 in b10)
5FHJ → 2CJC → C8C → 2CI → KC → B9 → 4F → 2I → 1F → F in b21 (c=10) (n=53296 in b10)
2BGIJ → CKKC → 64CI → BFI → 6F9 → 1HC → 9F → 69 → 2C → 13 → 3 in b21 (c=11) (n=498286 in b10)
FHKKK → AA5HI → GAJF → 4J89 → C8C → 2CI → KC → B9 → 4F → 2I → 1F → F in b21 (c=12) (n=3083912 in b10)
3BDGHJK → AHKKA3 → AA5HI → GAJF → 4J89 → C8C → 2CI → KC → B9 → 4F → 2I → 1F → F in b21 (c=13) (n=304907819 in b10)
6BBHIJJJJ → G1BHJ4DF → AHKKA3 → AA5HI → GAJF → 4J89 → C8C → 2CI → KC → B9 → 4F → 2I → 1F → F in b21 (c=14) (n=247765672579 in b10)
3DDGGGGGGGIIJ → 284GJDKAD63I → 5D65FHGK3 → 5BIB3KC → 1J6DC9 → H5JF → 2CJC → C8C → 2CI → KC → B9 → 4F → 2I → 1F → F in b21 (c=15) (n=26851272398708896 in b10)

Graph durch Euler

by in Arithmetic, Mathematics, Prime numbers and tagged , , , , , , , , , , , , , | Leave a comment

This is the famous Ulam spiral, in which prime numbers are represented on filled squares on a square spiral:

The Ulam spiral

I like the way the spiral sits between chaos and calm. It’s not wholly random and it’s not wholly regular — it’s betwixt and between. You get a similar chaos-and-calm vibe from a graph for a function called Euler phi. And primes are at work there too. Here’s the graph from Wikipedia:

Graph of eulerphi(n) = φ(n) (see Euler’s totient function)

But what is the Euler phi function? For any integer n, eulerphi(n) gives you the count of numbers < n that are relatively prime to n. That is, the count of numbers < n that have no common factors with n other than one. You can see how eulerphi(n) works by considering whether you can simplify the fraction a/b, where a = 1..n-1 and b = n:

φ(6) = 2
1/6 (1)
2/6 → 1/3
3/6 → 1/2
4/6 → 2/3
5/6, ∴ φ(6) = 2

φ(7) = 6
1/7 (1)
2/7 (2)
3/7 (3)
4/7 (4)
5/7 (5)
6/7, ∴ φ(7) = 6

φ(12) = 4
1/12 (1)
2/12 → 1/6
3/12 → 1/4
4/12 → 1/3
5/12 (2)
6/12 → 1/2
7/12 (3)
8/12 → 2/3
9/12 → 3/4
10/12 → 5/6
11/12, ∴ φ(12) = 4

φ(13) = 12
1/13 (1)
2/13 (2)
3/13 (3)
4/13 (4)
5/13 (5)
6/13 (6)
7/13 (7)
8/13 (8)
9/13 (9)
10/13 (10)
11/13 (11)
12/13, ∴ φ(13) = 12

As you can see, eulerphi(n) = n-1 for primes. Now you know what the top line of the Eulerphi graph is. It’s the primes. Here’s a bigger version of the graph:

Graph of eulerphi(n) = φ(n)

Unlike the Ulam spiral, however, the Eulerphi graph is cramped. But it’s easy to stretch it. You can represent φ(n) as a fraction between 0 and 1 like this: phifrac(n) = φ(n) / (n-1). Using phifrac(n), you can create Eulerphi bands, like this:

Eulerphi band, n <= 1781

Eulerphi band, n <= 3561

Eulerphi band, n <= 7121

Eulerphi band, n <= 14241

Or you can create Eulerphi discs, like this:

Eulerphi disc, n <= 1601

Eulerphi disc, n <= 3201

Eulerphi disc, n <= 6401

Eulerphi disc, n <= 12802

Eulerphi disc, n <= 25602

But what is the bottom line of the Eulerphi bands and inner ring of the Eulerphi discs, where φ(n) is smallest relative to n? Well, the top line or outer ring is the primes and the bottom line or inner ring is the primorials (and their multiples). The function primorial(n) is the multiple of the first n primes:

primorial(1) = 2
primorial(2) = 2*3 = 6
primorial(3) = 2*3*5 = 30
primorial(4) = 2*3*5*7 = 210
primorial(5) = 2*3*5*7*11 = 2310
primorial(6) = 2*3*5*7*11*13 = 30030
primorial(7) = 2*3*5*7*11*13*17 = 510510
primorial(8) = 2*3*5*7*11*13*17*19 = 9699690
primorial(9) = 2*3*5*7*11*13*17*19*23 = 223092870
primorial(10) = 2*3*5*7*11*13*17*19*23*29 = 6469693230

Here are the numbers returning record lows for φfrac(n) = φ(n) / (n-1):

φ(4) = 2 (2/3 = 0.666…)
4 = 2^2
φ(6) = 2 (2/5 = 0.4)
6 = 2.3
φ(12) = 4 (4/11 = 0.363636…)
12 = 2^2.3
[…]
φ(30) = 8 (8/29 = 0.275862…)
30 = 2.3.5
φ(60) = 16 (16/59 = 0.27118…)
60 = 2^2.3.5
[…]
φ(210) = 48 (48/209 = 0.229665…)
210 = 2.3.5.7
φ(420) = 96 (96/419 = 0.2291169…)
420 = 2^2.3.5.7
φ(630) = 144 (144/629 = 0.228934…)
630 = 2.3^2.5.7
[…]
φ(2310) = 480 (480/2309 = 0.2078822…)
2310 = 2.3.5.7.11
φ(4620) = 960 (960/4619 = 0.20783719…)
4620 = 2^2.3.5.7.11
[…]
30030 = 2.3.5.7.11.13
φ(60060) = 11520 (11520/60059 = 0.191811385…)
60060 = 2^2.3.5.7.11.13
φ(90090) = 17280 (17280/90089 = 0.1918103209…)
90090 = 2.3^2.5.7.11.13
[…]
φ(510510) = 92160 (92160/510509 = 0.18052571061…)
510510 = 2.3.5.7.11.13.17
φ(1021020) = 184320 (184320/1021019 = 0.18052553…)
1021020 = 2^2.3.5.7.11.13.17
φ(1531530) = 276480 (276480/1531529 = 0.180525474868579…)
1531530 = 2.3^2.5.7.11.13.17
φ(2042040) = 368640 (368640/2042039 = 0.18052544540040616…)
2042040 = 2^3.3.5.7.11.13.17

Primal Polynomial

by in Arithmetic, Mathematics, Prime numbers and tagged , , , | Leave a comment

n² + n + 17 is one of the best-known polynomial formulas for primes. Its values for n = 0 to 15 are all prime, starting with 17 and ending with 257. — David Wells in The Penguin Dictionary of Curious and Interesting Numbers (1986), entry for “17”

• 17, 19, 23, 29, 37, 47, 59, 73, 89, 107, 127, 149, 173, 199, 227, 257

Primal Pellicles

by in Arithmetic, Base Behavior, Integer Sequences, Mathematics, Prime numbers and tagged , , , , , , , , | Leave a comment

Numbers have thin skins. And they’re easily replaced. Take 71624133. Here it is permuting its pellicles:

71624133 in base 10 = 100010001001110010111000101 in base 2 = 11222202212211200 in b3 = 10101032113011 in b4 = 121313433013 in b5 = 11035053113 in b6 = 1526536500 in b7 = 421162705 in b8 = 158685750 in b9 = 374802A9 in b11 = 1BBA1199 in b12 = 11AB9B59 in b13 = 9726137 in b14 = 644BE73 in b15 = F3855B7 in b16

But if digits are the skin of 71624133, what are its bones? Well, you could say the skeleton of a number, something that doesn’t change from base to base, is its prime factorization:

71624133 = 32 × 72 × 162413

But the primes themselves are numbers, so they’re wearing pellicles too. And it turns out that, in base 10, the pellicles of the prime factors of 71624133 match the pellicle of 71624133 itself:

71624133 = 32.72.162413

Here’s a list of primal pellicles in base 10:

735 = 3.5.72
3792 = 24.3.79
1341275 = 52.13.4127
13115375 = 53.7.13.1153
22940075 = 52.229.4007
29373375 = 3.53.29.37.73
71624133 = 32.72.162413
311997175 = 52.7.172.31.199
319953792 = 27.3.53.79.199
1019127375 = 32.53.7.127.1019
1147983375 = 3.53.7.11.83.479
1734009275 = 52.173.400927
5581625072 = 24.5581.62507
7350032375 = 53.7.23.73.5003
17370159615 = 34.5.17.59.61.701
33061224492 = 22.33.306122449
103375535837 = 72.37.103.553583
171167303912 = 23.11.172.6730391
319383665913 = 3.133.19.383.6659
533671737975 = 34.52.17.53.367.797
2118067737975 = 32.52.7.79.211.80677
3111368374257 = 3.112.132.683.74257
3216177757191 = 3.73.191.757.21617
3740437158475 = 52.37.4043715847
3977292332775 = 3.52.292.233.277.977
4417149692375 = 53.7.23.4969.44171
7459655393232 = 24.32.72.23.45965539
7699132721175 = 3.52.72.27211.76991
7973529228735 = 3.5.7.972.2287.3529
10771673522535 = 34.5.67.71.107.52253

You can find them at the Online Encyclopedia of Integer Sequences under A121342, “Composite numbers that are a concatenation of their distinct prime divisors in some order.” But what about pairs of primal pellicles, that is, pairs of numbers where the prime factors of each form the pellicle of the other?

35 = 5.7 ↔ 75 = 3.52
1275 = 3.52.17 ↔ 3175 = 52.127
131715 = 32.5.2927 ↔ 329275 = 52.13171
3199767 = 3.359.2971 ↔ 35932971 = 3.19.67.972
14931092 = 22.11.61.5563 ↔ 116155632 = 24.3.109.1492

And here are a few primal pellicles I’ve found in other bases:

Primal Pellicles in Base 2

1111011011110 = 10.1110.110110111 in b2 = 7902 = 2.32.439 in b10
1110001100110111 = 1110.10111.100011001 in b2 = 58167 = 32.23.281 in b10
1111011011011110 = 10.1110.110110110111 in b2 = 63198 = 2.32.3511 in b10
11101001100001101 = 1110.101.101001100001 in b2 = 119565 = 32.5.2657 in b10
1111011011011011110 = 10.1110.110110110110111 in b2 = 505566 = 2.32.28087 in b10
1111011111101111011 = 1110.1011.10111.11011111 in b2 = 507771 = 32.11.23.223 in b10

Primal Pellicles in Base 3

121022 = 210.12.102 in b3 = 440 = 23.5.11 in b10
212212 = 22.21.212 in b3 = 644 = 22.7.23 in b10
20110112 = 210.201.1011 in b3 = 4712 = 23.19.31 in b10
21110110 = 10.212.1101 in b3 = 5439 = 3.72.37 in b10
121111101 = 122.111.1101 in b3 = 12025 = 52.13.37 in b10
222112121 = 22.21.221121 in b3 = 19348 = 22.7.691 in b10
2202122021 = 22.2021.22021 in b3 = 54412 = 22.61.223 in b10
120212201221 = 2.122.21.201.1202 in b3 = 312550 = 2.52.7.19.47 in b10

Primal Pellicles in Base 7

2525 = 2.52.25 in b7 = 950 = 2.52.19 in b10
3210 = 2.34.10 in b7 = 1134 = 2.34.7 in b10
5252 = 2.52.52 in b7 = 1850 = 2.52.37 in b10
332616 = 33.16.326 in b7 = 58617 = 33.13.167 in b10
336045 = 32.5.3604 in b7 = 59715 = 32.5.1327 in b10
2251635 = 22.3.5.16.252 in b7 = 281580 = 22.3.5.13.192 in b10

Primal Pellicles in Base 11

253 = 22.3.52 in b11 = 300 = 22.3.52 in b10
732 = 2.32.72 in b11 = 882 = 2.32.72 in b10
2123 = 23.33.12 in b11 = 2808 = 23.33.13 in b10
3432 = 25.3.43 in b11 = 4512 = 25.3.47 in b10
3710 = 32.72.10 in b11 = 4851 = 32.72.11 in b10
72252 = 23.72.225 in b11 = 105448 = 23.72.269 in b10

Primal Pellicles in Base 15

275 = 24.5.7 in b15 = 560 = 24.5.7 in b10
2D5 = 2.52.D in b15 = 650 = 2.52.13 in b10
2CD5 = 2.52.CD in b15 = 9650 = 2.52.193 in b10
7BE3 = 3.72.BE in b15 = 26313 = 3.72.179 in b10
21285 = 24.52.128 in b15 = 105200 = 24.52.263 in b10