Category Archives: Fractals
The Wyrm Ferns
A fern is a fractal, a shape that contains copies of itself at smaller and smaller scales. That is, part of a fern looks like the fern as a whole:
Fern as fractal (source)
Millions of years after Mother Nature, man got in on the fract, as it were:
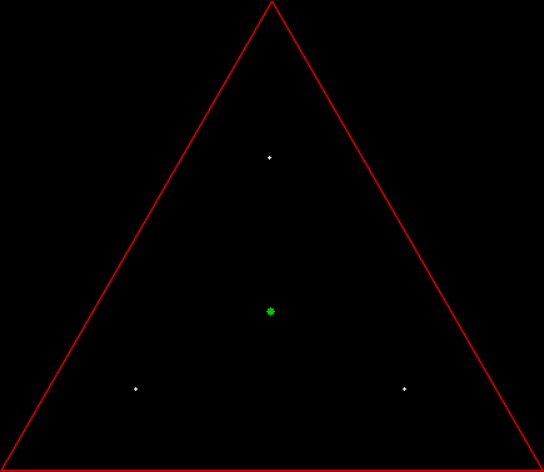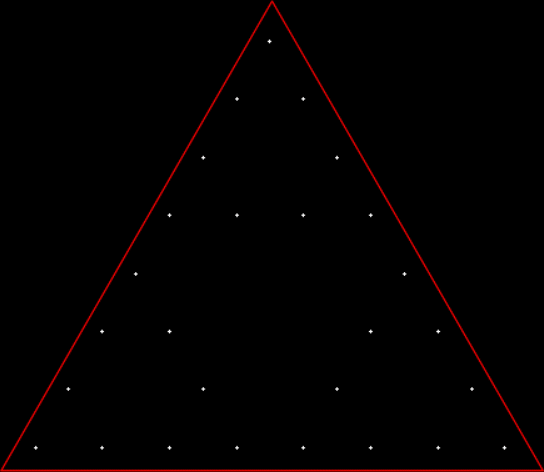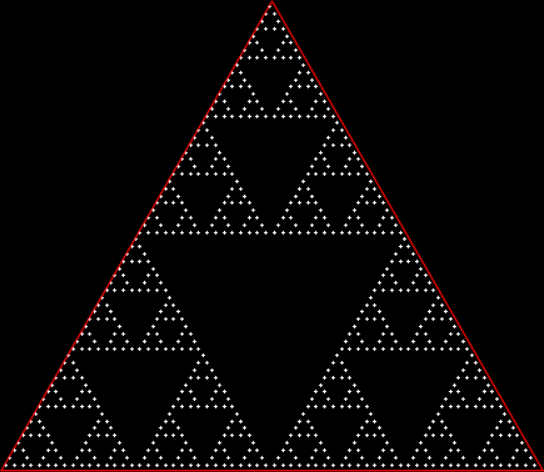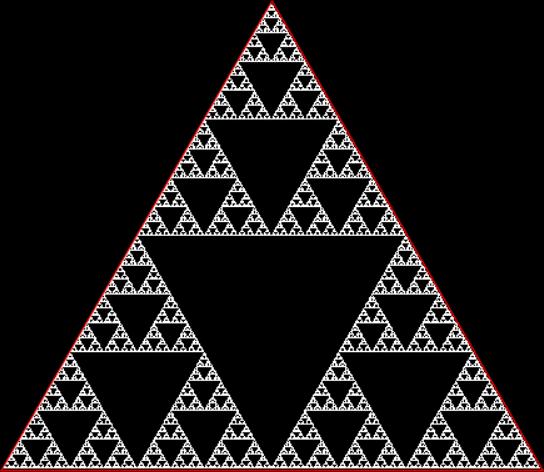
The Sierpiński triangle, a 2d fractal
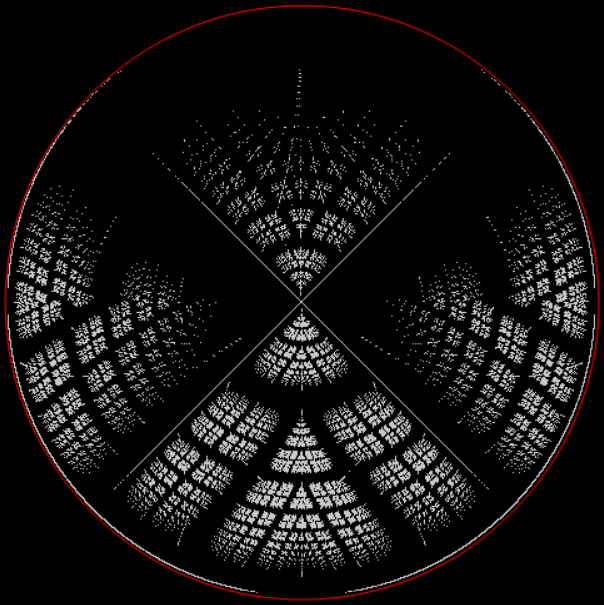
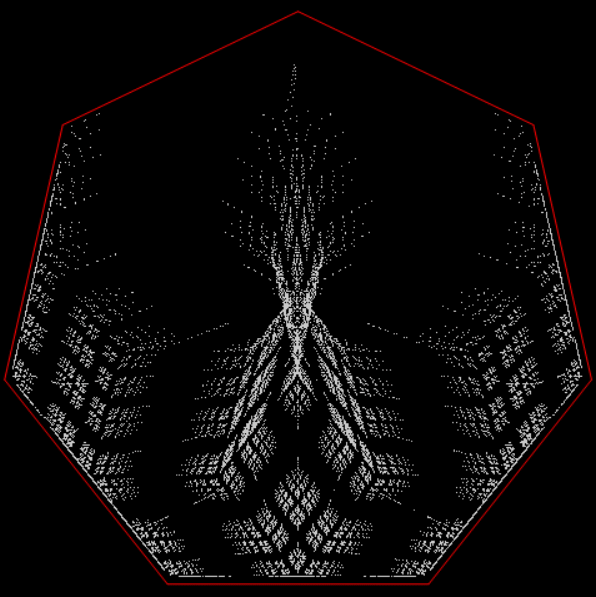
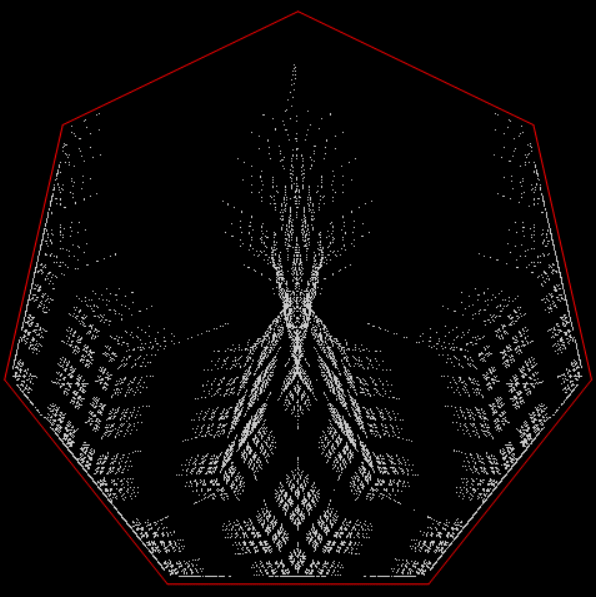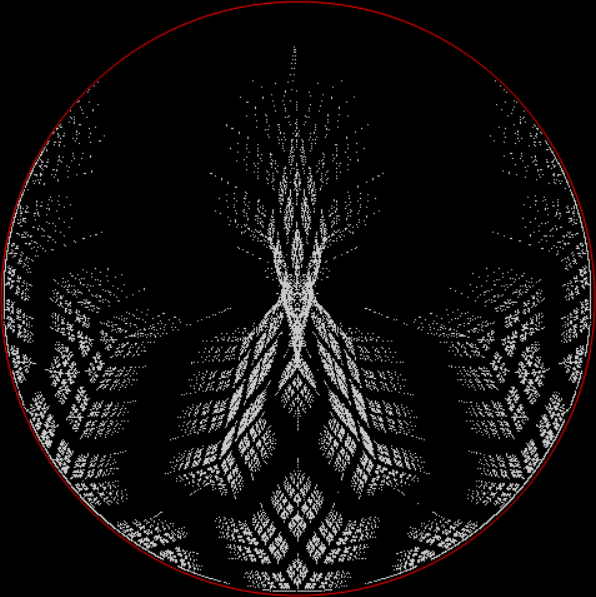
The Sierpiński triangle is a fractal created in two dimensions by a point jumping halfway towards one or another of the three vertices of a triangle. And here is a fractal created in one dimension by a point jumping halfway towards one or another of the two ends of a line:

A 1d fractal
In one dimension, the fractality of the fractal isn’t obvious. But you can try draggin’ out (or dragon out) the fractality of the fractal by ferning the wyrm, as it were. Suppose that after the point jumps halfway towards one or another of the two points, it’s rotated by some angle around the midpoint of the two original points. When you do that, the fractal becomes more and more obvious. In fact, it becomes what’s called a dragon curve (in Old English, “dragon” was wyrm or worm):
Fractal with angle = 5°
Fractal 10°
Fractal 15°
Fractal 20°
Fractal 25°
Fractal 30°
Fractal 35°
Fractal 40°
Fractal 45°
Fractal 50°
Fractal 55°
Fractal 60°
Fractal 0° to 60° (animated at ezGif)
But as the angle gets bigger, an interesting aesthetic question arises. When is the ferned wyrm, the dragon curve, at its most attractive? I’d say it’s when angle ≈ 55°:

Fractal 50°
Fractal 51°
Fractal 52°
Fractal 53°
Fractal 54°
Fractal 55°
Fractal 56°
Fractal 57°
Fractal 58°
Fractal 59°
Fractal 60°
Fractal 50° to 60° (animated)
At angle >= 57°, I think the dragon curve starts to look like some species of bristleworm, which are interesting but unattractive marine worms:
A bristleworm, Nereis virens (see polychaete at Wikipedia)
Finally, here’s what the ferned wyrm looks like in black-and-white and when it’s rotating:
Fractal 0° to 60° (b&w, animated)
Fractal 56° (rotating)
Fractal 56° (b&w, rotating)
Double fractal 56° (b&w, rotating)
Previously Pre-Posted (Please Peruse)…
• Curvous Energy — a first look at dragon curves
• Back to Drac’ — another look at dragon curves
Squaring the Triangle
It’s an interesting little exercise in elementary trigonometry to turn the Sierpiński triangle…
A Sierpiński triangle
…into its circular equivalent:
A Sierpiński trisc
You could call that a trisc, because it’s a triangle turned into a disc. And here’s triangle-and-trisc in one image:
Sierpiński triangle + Sierpiński trisc
But what’s the square equivalent of a Sierpiński triangle? This is:
Square from Sierpiński triangle
You can do that directly, as it were:
Sierpiński triangle → square
Or you can convert the triangle into a disc, then the disc into a square, like this:
Sierpiński triangle → trisc → square
Now try converting the triangle into a pentagon:

Pentagon from Sierpiński triangle
Sierpiński triangle → pentagon
Sierpiński triangle → trisc → pentagon
Hexagon from Sierpiński triangle
Sierpiński triangle → hexagon
Sierpiński triangle → trisc → hexagon
But you can also convert the Sierpiński trisc back into a Sierpiński triangle, then into a Sierpiński trisc again:
Sierpiński triangle → trisc → triangle → trisc
Sierpiński triangle → trisc → triangle → trisc (animated at Ezgif)
Sierpiński triangle → trisc → triangle → trisc (b&w)
Sierpiński triangle → trisc → triangle → trisc (b&w) (animated at Ezgif)
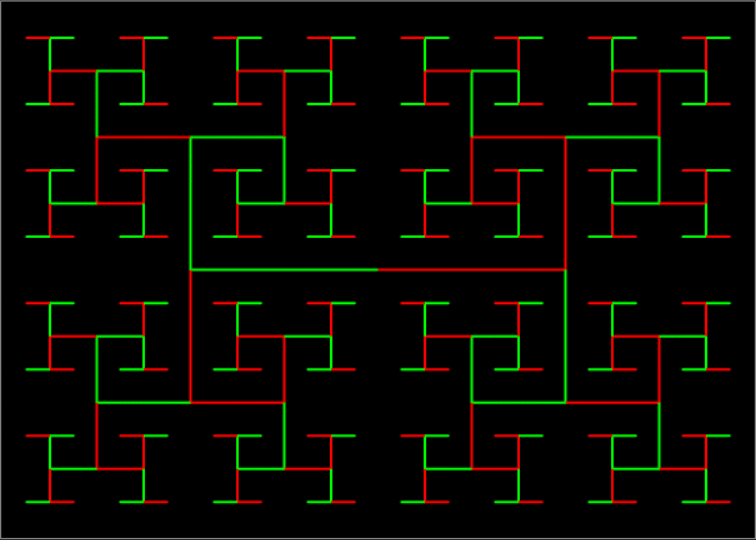
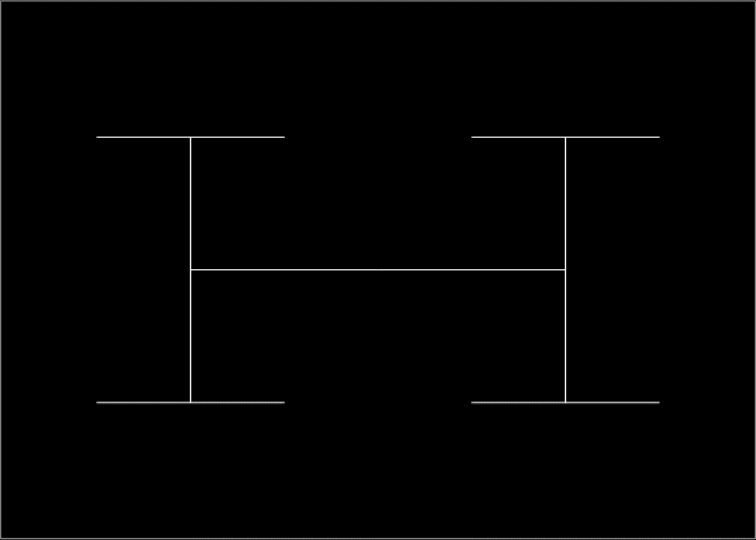
After triangles come squares. Here’s a shape called a T-square fractal:

And here’s the circular equivalent of a T-square fractal:

T-square fractal → T-squisc
T-square fractal + T-squisc
If a disc from a triangle is a trisc, then a disc from a square is a squisc (it would be pentisc, hexisc, heptisc for pentagonal, hexagonal and heptagonal fractals). Here’s the octagonal equivalent of a T-square fractal:
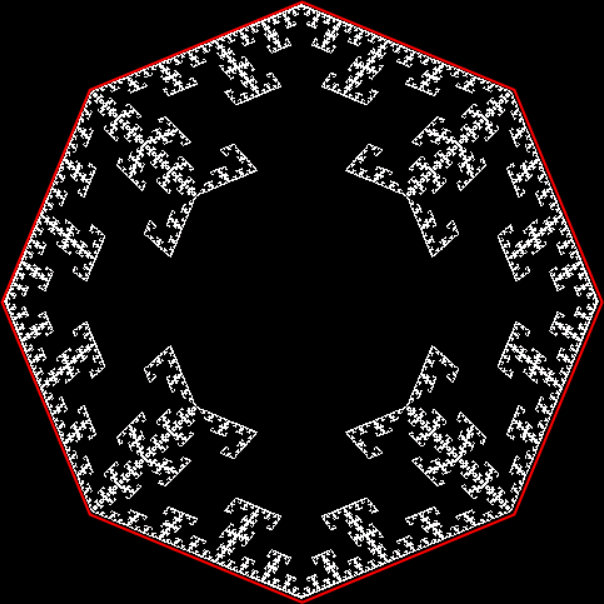
Octagon from T-square fractal
As with the Sierpiński trisc, you can use the T-squisc to create the T-octagon:

T-square fractal → T-squisc → T-octagon (color)
Or you can convert the T-square directly into the T-octagon:
T-square fractal to T-octagon fractal
But using the squisc makes for interesting multiple images:
T-square fractal → T-squisc → T-octagon (b&w)
T-square fractal → T-squisc → T-octagon → T-squisc
T-square fractal → T-squisc → T-octagon → T-squisc (animated at Ezgif)
The conversions from polygon to polygon look best when the number of sides in the higher polygon are a multiple of the number of sides in the lower, like this:
Sierpiński triangle → Sierpiński hexagon → Sierpiński nonagon
Scout the Routes
Triangles? Yes. Squares? No. If you scout the routes with a triangle, you get a beautiful fractal. If you scout the routes with a square, you don’t. Here’s what you get with a triangle:
A Sierpiński triangle
But how do you scout the routes? (That phrase works best in the American dialects where “scout” rhymes with “route”.) Simple: you mark the final positions reached when a point traces all possible ways of jumping, say, eight times 1/2-way towards the vertices of a polygon. Here’s an animation of a point scouting the routes of eight jumps towards the vertices of a triangle (it starts each time at the center):
Creating a Sierpiński triangle by scouting the routes (animated at Ezgif)
If you scout the routes with a square, you don’t get a fractal. Instead, the interior of the square fills evenly (and boringly) with the end-points of the routes:
Scouting the routes with a square (animated at Ezgif)
But you can create fractals with a square if you out routes as you scout routes. That is, if you exclude some routes and don’t mark their end-points. One way to do this is to compare the proposed next jump-vertex (vertex-jumped-towards) with the previous jump-vertex. For example, if the proposed jump-vertex, jv[t], is the same as the previous jump-vertex, jv[t-1], you don’t jump towards jv[t] or you jump towards it in a different way. The test is jv[t] = jv[t-1] + vi. If vi = 0 and you jump towards the clockwise neighbor of jv when the test is true, you get a fractal looking like this:
vi = 0, action = jv → jv + 1
Here’s the fractal if you jump towards the clockwise-neighbor-but-one when the test is true:
vi = 0, action = jv + 2
Now try varying the vi of the jv[t-1] + vi:
vi = 2, action = jv + 2
vi = 2, action = jv + 1
vi = 3, action = jv + 1
Or what about jumping in a different way towards jv when the test is true? If you jump 2/3 of the way rather 1/2, you get his fractal:
vi = 2, action = jump 2/3
And if you jump 4/3 of the way (i.e., you overshoot the vertex jv), you get this fractal:
vi = 0, action = jump 4/3rds to vertex
vi = 0, jump 4/3 (guide-square removed)
vi = 2, jump 4/3rds (guide-square removed)
And in this fractal the point jumps 2/3 of the way to the center of the square when the test is true:
vi = 2, action = jump 2/3rds of way to center of square
But why apply only one test to jv[1] and use only when one alternative jump? If jv[t] = jv[t-1] + 1 or jv[t] = jv[t-1] + 3, jv[t] becomes jv[t]+1 or jv[t]+3, respectively, you get this fractal:
vi = 1, jv + 1; vi = 3, jv + 3
Here are more fractals created by single and double tests:
vi = 1, jv + 1
vi = 0, jump 2/3
vi = 0, jump towards center 2/3rds
vi = 1, jump-center 2/3
vi = 2, jump 1/3; vi = 3, jump 1/1 (i.e, 1)
vi = 0, jv + 2; vi = 2, jump-center 1/2
vi = 0, jv + 2; vi = 2, jump-center 2/3
vi = 0, jv + 2; vi = 2, jump-center 4/3
vi = 0, jv + 1; vi = 2, jump 2/3
vi = 0, jv + 2; vi = 2, jump 2/3
vi = 0, jump 4/3; vi = 2, jv + 2
vi = 0, jump 2/3; vi = 2, jv + 1
vi = 0, jump 4/3; vi = 1, jv + 2
vi = 0, jump 2/3; vi = 2, jump 1/3
vi =0, jump 1/3; vi = 2, jump 2/3
vi = 0, jump 0/1 (i.e, 0); vi = 2, jump 1/3
Lime Time
What do you get if you list every successive pair of entries in this sequence?
1, 2, 1, 3, 2, 3, 1, 4, 3, 4, 1, 5, 2, 5, 3, 5, 4, 5, 1, 6, 5, 6, 1, 7, 2, 7, 3, 7, 4, 7, 5, 7, 6, 7, 1, 8, 3, 8, 5, 8, 7, 8, 1, 9, 2, 9, 4, 9, 5, 9, 7, 9, 8, 9, 1, 10, 3, 10, 7, 10, 9, 10, 1, 11, 2, 11, 3, 11, 4, 11, 5, 11, 6, 11, 7, 11, 8, 11, 9, 11, 10, 11, 1, 12, 5, 12, 7, 12, 11, 12, 1, 13, … — A038568 at the Online Encyclopedia of Integer Sequence
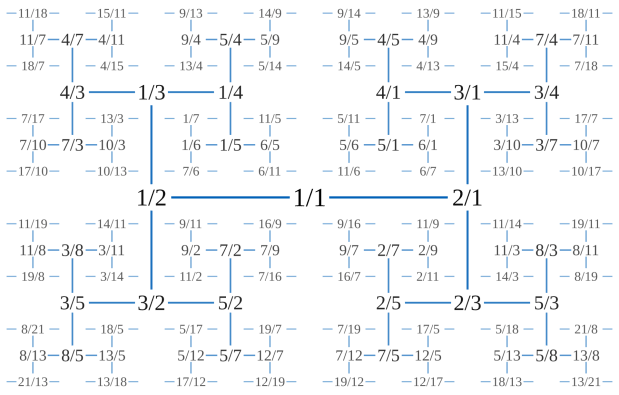
You get the rational fractions ordered by denominator in their simplest form: 1/2, 1/3, 2/3, 1/4, 3/4, 1/5, 2/5, 3/5… There are no pairs like 2/4 and 5/35, because those can be simplified: 2/4 → 1/2; 15/35 → 3/7. You can get the same set of rational fractions by listing every successive pair in this sequence, the Stern-Brocot sequence:
1, 2, 1, 3, 2, 3, 1, 4, 3, 5, 2, 5, 3, 4, 1, 5, 4, 7, 3, 8, 5, 7, 2, 7, 5, 8, 3, 7, 4, 5, 1, 6, 5, 9, 4, 11, 7, 10, 3, 11, 8, 13, 5, 12, 7, 9, 2, 9, 7, 12, 5, 13, 8, 11, 3, 10, 7, 11, 4, 9, 5, 6, 1, 7, 6, 11, 5, 14, 9, 13, 4, 15, 11, 18, 7, 17, 10, 13, 3, 14, 11, 19, 8, 21, 13, 18, 5, 17, 12, 19, … — A002487 at the OEIS
But the fractions don’t come ordered by denominator this time. In fact, they seem to come at random: 1/2, 1/3, 2/3, 1/4, 3/5, 2/5, 3/4, 1/5, 4/7, 3/8, 5/7, 2/7, 5/8… But they’re not random at all. There’s a complicated way of generating them and a simple way. An amazingly simple way, I think:
Moshe Newman proved that the fraction a(n+1)/a(n+2) can be generated from the previous fraction a(n)/a(n+1) = x by 1/(2*floor(x) + 1 – x). The successor function f(x) = 1/(floor(x) + 1 – frac(x)) can also be used. — A002487, “Stern-Brocot Sequence”, at the OEIS
In another form, the Stern-Brocot sequence is generated by what’s called the Calkin-Wilf Tree. Now suppose you use the Stern-Brocot sequence to supply the x co-ordinate of an L-graph whose arms run from 0 to 1. And you use the Calkin-Wilf Tree to supply the y co-ordinate of the L-tree. What do you get? As I described in “I Like Gryke”, you get this fractal:
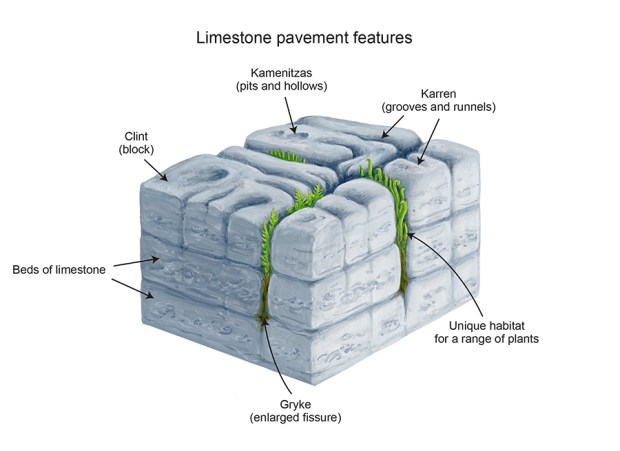
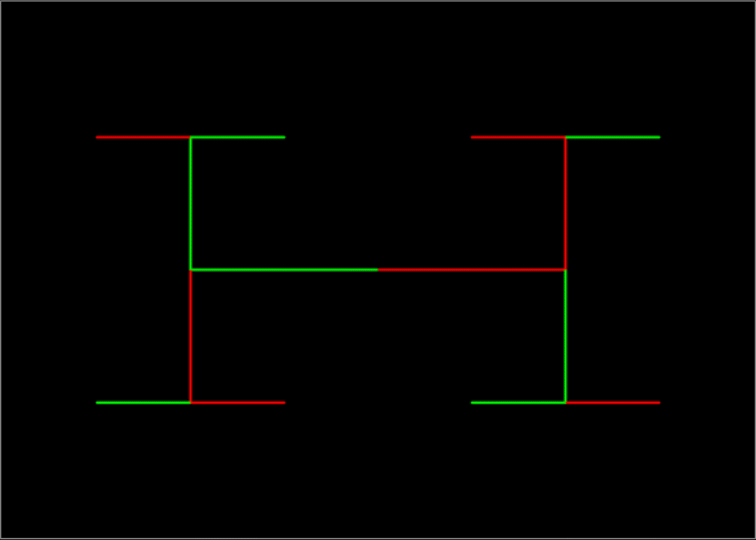
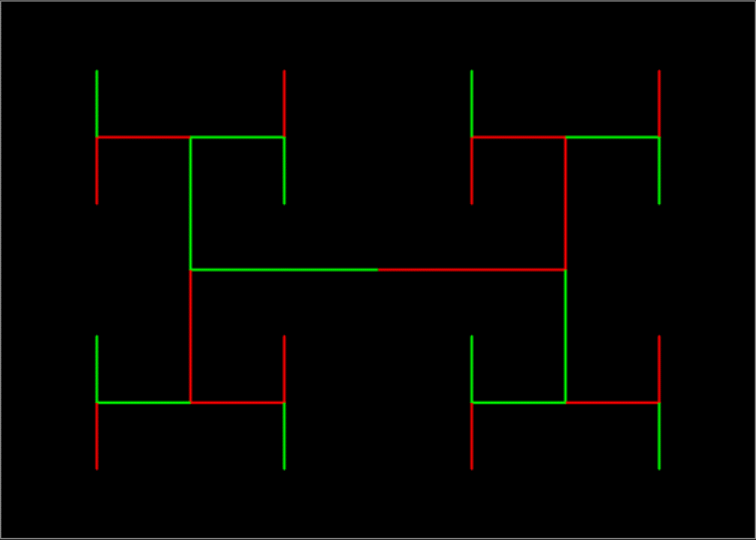
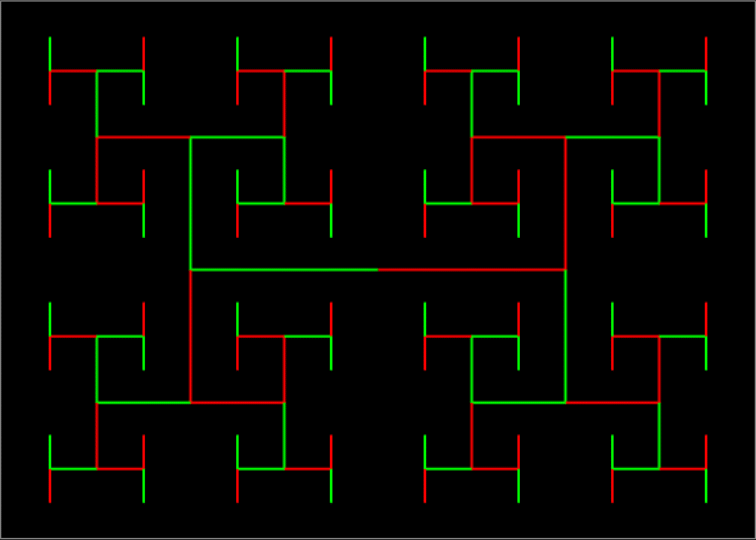
Limestone fractal
I call it a limestone fractal or pavement fractal or gryke fractal, because it reminds me of the fissured patterns you see in the limestone pavements of the Yorkshire Dales:
Fissured limestone pavement, Yorkshire Dales (Wikipedia)
But what happens when you plot the (x,y) of the Stern-Brocot sequence and the Calkin-Wilf Tree on a circle instead? You get an interestingly distorted limestone fractal:

Limestone fractal on circle
You can also plot the (x,y) around the perimeter of a polygon, then stretch the polygon into a circle. Here’s a square:

Limestone fractal on square
⇓
Limestone square stretched to circle
And here are a pentagon, hexagon, heptagon and octagon — note the interesting perspective effects:

Limestone fractal on pentagon
⇓
Limestone pentagon stretched to circle
Limestone fractal on hexagon
⇓
Limestone hexagon stretched to circle
Limestone fractal on heptagon
⇓
Limestone heptagon stretched to circle
Limestone fractal on octagon
⇓
Limestone octagon stretched to circle
And finally, here are animations of limestone polygons stretching to circles:
Limestone square stretched to circle (animated at EZgif)
Limestone pentagon to circle (animated)
Limestone hexagon to circle (animated)
Limestone heptagon to circle (animated)
Limestone octagon to circle (animated)
Previously Pre-Posted (Please Peruse)
• I Like Gryke — a first look at the limestone fractal
I Like Gryke
Sometimes I find fractals. And sometimes fractals find me. Here’s a fractal that found me:
Limestone fractal #1
I call it a limestone fractal or pavement fractal or gryke fractal, because it reminds me of the fissured patterns you see in the limestone pavements of the Yorkshire Dales:
Fissured limestone pavement, Yorkshire Dales (Wikipedia)
The limestone blocks are called clints and the larger fissures between them are called grykes, with kamenitza and karren (from Slavic and German, respectively) for smaller pits and grooves:
Limestone linguistics (Dales Rocks)
Here’s the me-finding fractal again, in a slightly different version:
Limestone fractal #2
How did it find me? Well, I wasn’t looking for fractals, but looking at fractions. Farey fractions and Calkin-Wilf fractions, to be precise. They can both be represented as bifurcating trees, like this:
Calkin-Wilf tree (Wikipedia)
Both trees produce all the irreducible rational fractions — but in a different order. That’s why they create a fractal (rather than a 45° line). By following the same path in both bifurcating trees, I generated parallel sequences of Farey and Calkin-Wilf fractions, then used the Farey fractions to represent x in a 1×1 square and the Calkin-Wilf fractions to represent y (where the Calkin-Wilfs, a/b, were greater than 1, I simply a/b → b/a). When you do that (or use Stern-Brocot fractions instead of the Farey fractions), you get the limestone fractal.
I think it looks better in the second version (which is the one that found me, in fact). For LF #2, I was using standard binary numbers to generate the parallel sequences, so the leftmost digit was always 1 and final step of the tree-search was always in the same direction. Here’s LF #2 as black-on-white rather than white-on-black:
Limestone fractal #2 (black-on-white)
And here is the formation of LF #1 as an animated gif:

Growth of limestone fractal (animated at ezGIF)
And if that’s a me-finding fractal, what about me-found fractals? Here’s one:

The Hourglass Fractal (animated gif optimized at ezGIF)
Hourglass fractal
I can say “I found that fractal” because I was looking for fractals when it appeared on the screen. And re-appeared (and re-re-appeared), because I’ve found it using different methods.
Elsewhere Other-Accessible
• Hour Power — more on the hourglass fractal
Deep-Dive Dyadendricity
This simple equation helps you understand a fractal:
1 + 1/2 + 1/4 + 1/8 + 1/16 + 1/32 + … = 2 = Σ(1/2k,k=0..∞)
Now here’s the construction of the H-tree fractal, in which the lines are divided in length by sqrt(2) = 1.41421356237… at each stage. Or multiplied by 0.70710678118… = &sqrt;0.5. This means that, after two divisions, the lines are 1/2 the size. So in the end they create a 1 x &sqrt;2 rectangle:
H-Tree fractal #1
H-Tree fractal #2
H-Tree fractal #3
H-Tree fractal #4
H-Tree fractal #5
H-Tree fractal #6
H-Tree fractal #7
H-Tree fractal #8
H-Tree fractal #9
H-Tree fractal #10
↓
[…]
↓
H-Tree fractal #13
H-Tree fractal #14
H-Tree fractal #15
Here’s an animation:
H-Tree fractal (animated at EZgif)
And here’s the H-tree in black-and-white:
H-Tree fractal #3
↓
H-Tree fractal #6
↓
H-Tree fractal #6
↓
H-Tree fractal #12
↓
H-Tree fractal #15
↓
H-Tree fractal (animated at EZgif)
Because the construction of the H-tree is governed by a string of directions — for example, left-right-right-left-left-left… or 211222… — you can perform tests on that string to create sub-fractals from the super-fractal. Like this:
count(1) = count(2) in string to step 12
count(1) = count(2) in string (omitting lines)
sum(string) = mul(string)
sum(string) > mul(string)
count(1) = 2 or count(2) = 2 after step 2
count(1) < count(2)
count(1) < 3 or count(2) < 3 after step 6
value of string after step 8 > value of string at step 1
value after step 8 > value at step 4
value after step 8 < value step 1
ispalindrome(string) to step 11
ispalindrome(string) to step 18
ispalindrome(string) to step 20
alternating 121… or 212… in string after step 9
ispolygonal(sum(string[i]-1),pol=10)
isprime(sum(string))
sum(string[i]-1) mod 13 = 0
sum(string[i]-1) mod 13 = 1
sum(string[i]-1) mod 16 = 0
sum(string[i]-1) mod 18 = 0
Mathematicoynte
Pre-previously, I looked at a fractal phallus. Now I want to look at a fractal fanny (in the older British sense). In fact, it’s a fractional fractal fanny. Take a look at these fractions:
1/10, 1/9, 1/8, 1/7, 1/6, 1/5, 2/10, 2/9, 1/4, 2/8, 2/7, 3/10, 1/3, 2/6, 3/9, 3/8, 2/5, 4/10, 3/7, 4/9, 1/2, 2/4, 3/6, 4/8, 5/10, 5/9, 4/7, 3/5, 6/10, 5/8, 2/3, 4/6, 6/9, 7/10, 5/7, 3/4, 6/8, 7/9, 4/5, 8/10, 5/6, 6/7, 7/8, 8/9, 9/10
They’re all the fractions for 1/2..(n-1)/n, n = 10, sorted by increasing size. But obviously some of them are the same: 1/2 = 2/4 = 3/6 = 5/10, 1/3 = 2/6 = 3/9, 1/4 = 2/8, and so on. If you remove the duplicates, you get this set of reduced fractions:
1/10, 1/9, 1/8, 1/7, 1/6, 1/5, 2/9, 1/4, 2/7, 3/10, 1/3, 3/8, 2/5, 3/7, 4/9, 1/2, 5/9, 4/7, 3/5, 5/8, 2/3, 7/10, 5/7, 3/4, 7/9, 4/5, 5/6, 6/7, 7/8, 8/9, 9/10
Now here are the reduced fractions for 1/2..(n-1)/n, n = 30:
1/30, 1/29, 1/28, 1/27, 1/26, 1/25, 1/24, 1/23, 1/22, 1/21, 1/20, 1/19, 1/18, 1/17, 1/16, 1/15, 2/29, 1/14, 2/27, 1/13, 2/25, 1/12, 2/23, 1/11, 2/21, 1/10, 3/29, 2/19, 3/28, 1/9, 3/26, 2/17, 3/25, 1/8, 3/23, 2/15, 3/22, 4/29, 1/7, 4/27, 3/20, 2/13, 3/19, 4/25, 1/6, 5/29, 4/23, 3/17, 5/28, 2/11, 5/27, 3/16, 4/21, 5/26, 1/5, 6/29, 5/24, 4/19, 3/14, 5/23, 2/9, 5/22, 3/13, 7/30, 4/17, 5/21, 6/25, 7/29, 1/4, 7/27, 6/23, 5/19, 4/15, 7/26, 3/11, 8/29, 5/18, 7/25, 2/7, 7/24, 5/17, 8/27, 3/10, 7/23, 4/13, 9/29, 5/16, 6/19, 7/22, 8/25, 9/28, 1/3, 10/29, 9/26, 8/23, 7/20, 6/17, 5/14, 9/25, 4/11, 11/30, 7/19, 10/27, 3/8, 11/29, 8/21, 5/13, 7/18, 9/23, 11/28, 2/5, 11/27, 9/22, 7/17, 12/29, 5/12, 8/19, 11/26, 3/7, 13/30, 10/23, 7/16, 11/25, 4/9, 13/29, 9/20, 5/11, 11/24, 6/13, 13/28, 7/15, 8/17, 9/19, 10/21, 11/23, 12/25, 13/27, 14/29, 1/2, 15/29, 14/27, 13/25, 12/23, 11/21, 10/19, 9/17, 8/15, 15/28, 7/13, 13/24, 6/11, 11/20, 16/29, 5/9, 14/25, 9/16, 13/23, 17/30, 4/7, 15/26, 11/19, 7/12, 17/29, 10/17, 13/22, 16/27, 3/5, 17/28, 14/23, 11/18, 8/13, 13/21, 18/29, 5/8, 17/27, 12/19, 19/30, 7/11, 16/25, 9/14, 11/17, 13/20, 15/23, 17/26, 19/29, 2/3, 19/28, 17/25, 15/22, 13/19, 11/16, 20/29, 9/13, 16/23, 7/10, 19/27, 12/17, 17/24, 5/7, 18/25, 13/18, 21/29, 8/11, 19/26, 11/15, 14/19, 17/23, 20/27, 3/4, 22/29, 19/25, 16/21, 13/17, 23/30, 10/13, 17/22, 7/9, 18/23, 11/14, 15/19, 19/24, 23/29, 4/5, 21/26, 17/21, 13/16, 22/27, 9/11, 23/28, 14/17, 19/23, 24/29, 5/6, 21/25, 16/19, 11/13, 17/20, 23/27, 6/7, 25/29, 19/22, 13/15, 20/23, 7/8, 22/25, 15/17, 23/26, 8/9, 25/28, 17/19, 26/29, 9/10, 19/21, 10/11, 21/23, 11/12, 23/25, 12/13, 25/27, 13/14, 27/29, 14/15, 15/16, 16/17, 17/18, 18/19, 19/20, 20/21, 21/22, 22/23, 23/24, 24/25, 25/26, 26/27, 27/28, 28/29, 29/30
Can you see the fractal fanny? Not unless you’re superhuman. But any normal human can see the fractal fanny when you turn those reduced and sorted fractions, a/b, into a graph, where y = b and x = n for a/bn:
graph for b of reduced a/b = 1/2..29/30, sorted by size of a/b
(click for larger)
If you don’t reduce the fractions, you get this distorted coynte:
graph for b of all fractions 1/2..29/30, sorted by a/b
And you can use other variables for y, like the sum of the continued fraction of a/b:
graph for sum(contfrac(a/b)) of reduced fractions 1/2..29/30, sorted by a/b
graph for cfsum of all fractions 1/2..29/30, sorted by a/b
And the product of the continued fraction of a/b:
graph for prod(contfrac(a/b)) of reduced fractions 1/2..29/30, sorted by a/b
graph for cfmul of all fractions 1/2..29/30, sorted by a/b
And you can sort by the size of other variables, like the number of factors of b:
graph for a+b of all fractions 1/2..29/30, sorted by factornum(b)
And so on:
graph for a of reduced fractions 1/2..29/30, sorted by a/b
graph for a of reduced fractions 1/2..29/30, sorted by a/b
graph for a of all fractions 1/2..29/30, sorted by a/b
graph for a of all fractions 1/2..29/30, sorted by length(contfrac(a/b))
graph for a of all fractions 1/2..29/30, sorted by factornum(b)
graph for a of all fractions 1/2..29/30, sorted by gcd(a/b)
graph for a+b of all fractions 1/2..29/30, sorted by a/b
graph for a+b of reduced fractions 1/2..29/30, sorted by a/b
graph for a+b of all fractions 1/2..29/30, sorted by a+b
graph for a+b of all fractions 1/2..29/30, sorted by cflen(a/b)
graph for a+b of all fractions 1/2..29/30, sorted by gbd(a,b)
graph for b of all fractions 1/2..29/30, sorted by a+b
graph for b of all fractions 1/2..29/30, sorted by cflen(a/b)
graph for b of all fractions 1/2..29/30, sorted by factnum(b)
graph for b of all fractions 1/2..29/30, sorted by gcd(a,b)
graph for b-a of all fractions 1/2..29/30, sorted by a/b
graph for b-a of reduced fractions 1/2..29/30, sorted by a/b
graph for b-a of all fractions 1/2..29/30, sorted by a+b
graph for b-a of all fractions 1/2..29/30, sorted by factnum(b)
graph for cfmul of all fractions 1/2..29/30, sorted by a
graph for cfsum of all fractions 1/2..29/30, sorted by a
Previously Pre-Posted (Please Peruse)
• Phrallic Frolics — a look at fractal phalluses, a.k.a. phralluses
Mods and Clockers
To understand clock-arithmetic, simply picture a clock-face with one hand and a big fat 0 in place of the 12. Now you can do some clock-arithmetic. For example, set the hour-hand to 5, then move on 4 hours. You’ve done this sum:
5 + 4 → 9
Now try 9 + 7. The hour-hand is already on 9, so move forward 7 hours:
9 + 7 → 4
Now try 3 + 8 + 1:
3 + 8 + 1 → 0
And 3 * 4:
4 * 3 = 4 + 4 + 4 → 0
That’s clock-arithmetic. But you’re not confined to 12-hour clocks. Here’s a 7-hour clock, where the 7 is replaced with a 0:
3 + 1 → 4
4 + 5 → 2
2 + 4 + 1 → 0
3 * 3 = 3 + 3 + 3 → 2
Another name for clock-arithmetic is modular arithmetic, because the clocks model the process of dividing a number by 12 or 7 and finding the remainder or residue — 12 or 7 is known as the modulus (and modulo is Latin for “by the modulus”).
5 + 4 = 9 → 9 / 12 = 0*12 + 9
(5 + 4) modulo 12 = 9
3 + 8 + 1 = 12 → 12 / 12 = 1*12 + 0
(3 + 8 + 1) modulo 12 = 0
19 / 12 = 1*12 + 7
19 mod 12 = 7
3 + 1 = 4 → 4 / 7 = 0*7 + 4
(3 + 1) mod 7 = 4
2 + 4 + 1 = 7 → 7 / 7 = 1*7 + 0
(2 + 4 + 1) mod 7 = 0
19 / 7 = 2*7 + 5
19 mod 7 = 5
Modular arithmetic can do wonderful things. One small but beautiful example is the way it can uncover hidden fractals in Pascal’s triangle:
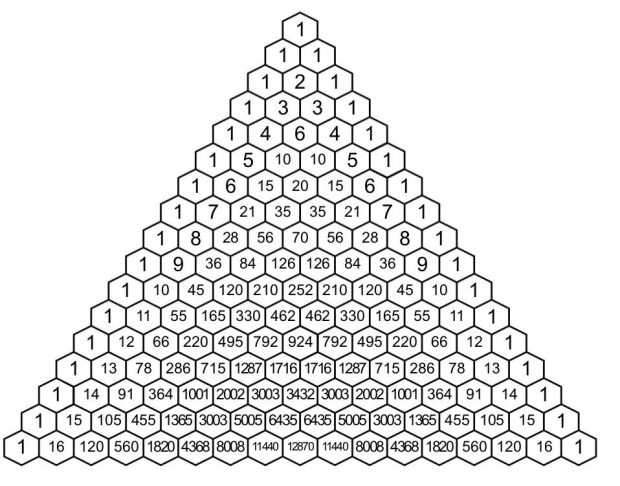
Pascal’s Triangle (via Desmos)
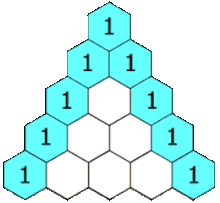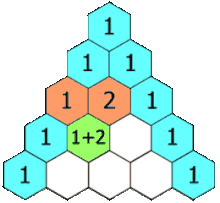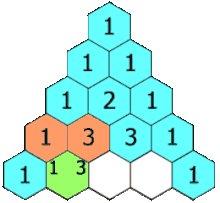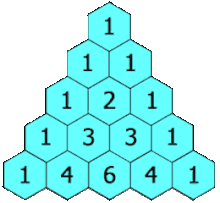
How to create Pascal’s triangle (via Wikipedia)
If you color all numbers n mod 2 = 1 (i.e., odd numbers) in the triangle, they create the famous Sierpiński triangle:

The Sierpiński triangle in Pascal’s triangle (via Fractal Foundation)
↓
Pascal’s triangle, n mod 2 = 1 (click for larger)
The Sierpiński triangle appears like this for all n mod 4 = 2 in Pascal’s triangle:
Pascal’s triangle, n mod 4 = 2 (click for larger)
And so on:
Pascal’s triangle, n mod 8 = 4
Pascal’s triangle, n mod 16 = 8
Pascal’s triangle, n mod 32 = 16
Pascal’s triangle, n mod 64 = 32
Pascal’s triangle, n mod 128 = 64
Pascal’s triangle, n mod 256 = 128
Pascal’s triangle, n mod 2,4,8… = 1,2,4… (animated via EzGif)
Post-Performative Post-Scriptum
There’s no need to calculate Pascal’s triangle in full to find the fractals above. The 10th row of Pascal’s triangle is this:
1, 10, 45, 120, 210, 252, 210, 120, 45, 10, 1
The 20th row is this:
1, 20, 190, 1140, 4845, 15504, 38760, 77520, 125970, 167960, 184756, 167960, 125970, 77520, 38760, 15504, 4845, 1140, 190, 20, 1
And the 29th is this:
1, 29, 406, 3654, 23751, 118755, 475020, 1560780, 4292145, 10015005, 20030010, 34597290, 51895935, 67863915, 77558760, 77558760, 67863915, 51895935, 34597290, 20030010, 10015005, 4292145, 1560780, 475020, 118755, 23751, 3654, 406, 29, 1
But you don’t need to consider those ever-growing numbers in the triangle when you’re finding fractals with modular arithmetic. When the modulus is 2, you just work with 0 and 1, that is, you add the previous numbers in the triangle and find the sum modulo 2. When the modulus is 4, you just work with 0, 1, 2 and 3, adding the numbers and finding the sum modulo 4. When it’s 8, you just work with 0, 1, 2, 3, 4, 5, 6 and 7, finding the sum modulo 8. And so on.
Fabulous Furry Fibonacci Fractal
At least, I think it’s a fractal. I came across it when I was counting the ways in which the integers can be the sum of distinct Fibonacci numbers. Here for reference is the Fibonacci sequence, the beautiful and endlessly fertile sequence that’s seeded with “1, 1” and continued by summing the two previous numbers:
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946, 17711, 28657, 46368, 75025, 121393, 196418, 317811, 514229, 832040…
I noticed some interesting patterns in the distinct-fib-num-sum count for the integers:
1 = 1 (count=1)
2 = 2 (count=1)
3 = 1+2 = 3 (count=2)
4 = 1+3 (c=1)
5 = 2+3 = 5 (c=2)
6 = 1+2+3 = 1+5 (c=2)
7 = 2+5 (c=1)
8 = 1+2+5 = 3+5 = 8 (c=3)
9 = 1+3+5 = 1+8 (c=2)
10 = 2+3+5 = 2+8 (c=2)
11 = 1+2+3+5 = 1+2+8 = 3+8 (c=3)
12 = 1+3+8 (c=1)
13 = 2+3+8 = 5+8 = 13 (c=3)
14 = 1+2+3+8 = 1+5+8 = 1+13 (c=3)
15 = 2+5+8 = 2+13 (c=2)
16 = 1+2+5+8 = 3+5+8 = 1+2+13 = 3+13 (c=4)
17 = 1+3+5+8 = 1+3+13 (c=2)
18 = 2+3+5+8 = 2+3+13 = 5+13 (c=3)
19 = 1+2+3+5+8 = 1+2+3+13 = 1+5+13 (c=3)
20 = 2+5+13 (c=1)
21 = 1+2+5+13 = 3+5+13 = 8+13 = 21 (c=4)
22 = 1+3+5+13 = 1+8+13 = 1+21 (c=3)
23 = 2+3+5+13 = 2+8+13 = 2+21 (c=3)
24 = 1+2+3+5+13 = 1+2+8+13 = 3+8+13 = 1+2+21 = 3+21 (c=5)
25 = 1+3+8+13 = 1+3+21 (c=2)
26 = 2+3+8+13 = 5+8+13 = 2+3+21 = 5+21 (c=4)
27 = 1+2+3+8+13 = 1+5+8+13 = 1+2+3+21 = 1+5+21 (c=4)
28 = 2+5+8+13 = 2+5+21 (c=2)
29 = 1+2+5+8+13 = 3+5+8+13 = 1+2+5+21 = 3+5+21 = 8+21 (c=5)
30 = 1+3+5+8+13 = 1+3+5+21 = 1+8+21 (c=3)
31 = 2+3+5+8+13 = 2+3+5+21 = 2+8+21 (c=3)
32 = 1+2+3+5+8+13 = 1+2+3+5+21 = 1+2+8+21 = 3+8+21 (c=4)
33 = 1+3+8+21 (c=1)
34 = 2+3+8+21 = 5+8+21 = 13+21 = 34 (c=4)
35 = 1+2+3+8+21 = 1+5+8+21 = 1+13+21 = 1+34 (c=4)
36 = 2+5+8+21 = 2+13+21 = 2+34 (c=3)
37 = 1+2+5+8+21 = 3+5+8+21 = 1+2+13+21 = 3+13+21 = 1+2+34 = 3+34
(c=6)
38 = 1+3+5+8+21 = 1+3+13+21 = 1+3+34 (c=3)
39 = 2+3+5+8+21 = 2+3+13+21 = 5+13+21 = 2+3+34 = 5+34 (c=5)
40 = 1+2+3+5+8+21 = 1+2+3+13+21 = 1+5+13+21 = 1+2+3+34 = 1+5+34
(c=5)
41 = 2+5+13+21 = 2+5+34 (c=2)
42 = 1+2+5+13+21 = 3+5+13+21 = 8+13+21 = 1+2+5+34 = 3+5+34 = 8+3
4 (c=6)
43 = 1+3+5+13+21 = 1+8+13+21 = 1+3+5+34 = 1+8+34 (c=4)
44 = 2+3+5+13+21 = 2+8+13+21 = 2+3+5+34 = 2+8+34 (c=4)
45 = 1+2+3+5+13+21 = 1+2+8+13+21 = 3+8+13+21 = 1+2+3+5+34 = 1+2+
8+34 = 3+8+34 (c=6)
46 = 1+3+8+13+21 = 1+3+8+34 (c=2)
47 = 2+3+8+13+21 = 5+8+13+21 = 2+3+8+34 = 5+8+34 = 13+34 (c=5)
48 = 1+2+3+8+13+21 = 1+5+8+13+21 = 1+2+3+8+34 = 1+5+8+34 = 1+13+
34 (c=5)
49 = 2+5+8+13+21 = 2+5+8+34 = 2+13+34 (c=3)
50 = 1+2+5+8+13+21 = 3+5+8+13+21 = 1+2+5+8+34 = 3+5+8+34 = 1+2+1
3+34 = 3+13+34 (c=6)
51 = 1+3+5+8+13+21 = 1+3+5+8+34 = 1+3+13+34 (c=3)
52 = 2+3+5+8+13+21 = 2+3+5+8+34 = 2+3+13+34 = 5+13+34 (c=4)
53 = 1+2+3+5+8+13+21 = 1+2+3+5+8+34 = 1+2+3+13+34 = 1+5+13+34 (c=4)
54 = 2+5+13+34 (c=1)
55 = 1+2+5+13+34 = 3+5+13+34 = 8+13+34 = 21+34 = 55 (c=5)
56 = 1+3+5+13+34 = 1+8+13+34 = 1+21+34 = 1+55 (c=4)
The patterns are easier to see when the counts are set out like this:
1, 1, 2, 1, 2, 2, 1, 3, 2, 2, 3, 1, 3, 3, 2, 4, 2, 3, 3, 1, 4, 3, 3, 5, 2, 4, 4, 2, 5, 3, 3, 4, 1, 4, 4, 3, 6, 3, 5, 5, 2, 6, 4, 4, 6, 2, 5, 5, 3, 6, 3, 4, 4, 1, 5, 4, 4, 7, 3, 6, 6, 3, 8, 5, 5, 7, 2, 6, 6, 4, 8, 4, 6, 6, 2, 7, 5, 5, 8, 3, 6, 6, 3, 7, 4, 4, 5, 1, 5, 5, 4, 8, 4, 7, 7, 3, 9, 6, 6, 9, 3, 8, 8, 5, 10, 5, 7, 7, 2, 8, 6, 6, 10, 4, 8, 8, 4, 10, 6, 6, 8, 2, 7, 7, 5, 10, 5, 8, 8, 3, 9, 6, 6, 9, 3, 7, 7, 4, 8, 4, 5, 5, 1, 6, 5, 5, 9, 4, 8, 8… 1… — See A000119, Number of representations of n as a sum of distinct Fibonacci numbers, at the Online Encyclopedia of Integer Sequences (OEIS)
The numbers between each pair of 1s are symmetrical:
1, 2, 1,
1, 2, 2, 1,
1, 3, 2, 2, 3, 1,
1, 3, 3, 2, 4, 2, 3, 3, 1
1, 4, 3, 3, 5, 2, 4, 4, 2, 5, 3, 3, 4, 1
And when fibsumcount(n) = 1, then n = fib(i)-1, i.e. n is one less than a Fibonacci number:
1 = 1 (c=1)
2 = 2 (c=1)
4 = 1+3 (c=1)
7 = 2+5 (c=1)
12 = 1+3+8 (c=1)
20 = 2+5+13 (c=1)
33 = 1+3+8+21 (c=1)
54 = 2+5+13+34 (c=1)
88 = 1+3+8+21+55 (c=1)
143 = 2+5+13+34+89 (c=1)
232 = 1+3+8+21+55+144 (c=1)
376 = 2+5+13+34+89+233 (c=1)
609 = 1+3+8+21+55+144+377 (c=1)
986 = 2+5+13+34+89+233+610 (c=1)
1596 = 1+3+8+21+55+144+377+987 (c=1)
2583 = 2+5+13+34+89+233+610+1597 (c=1)
4180 = 1+3+8+21+55+144+377+987+2584 (c=1)
6764 = 2+5+13+34+89+233+610+1597+4181 (c=1)
10945 = 1+3+8+21+55+144+377+987+2584+6765 (c=1)
17710 = 2+5+13+34+89+233+610+1597+4181+10946 (c=1)
[…]
I also noticed a pattern relating to the maximum count reached in the numbers between the 1s. Suppose the function max(fib(i)-1..fib(i+1)-1) returns the highest count of ways to represent the numbers from fib(i)-1 to fib(i+1)-1. Notice how max() increases:
max(2..4) = 2
max(4..7) = 2
max(7..12) = 3
max(12..20) = 4
max(20..33) = 5
max(33..54) = 6
max(54..88) = 8
max(88..143) = 10
max(143..232) = 13
max(232..376) = 16
max(376..609) = 21
max(609..986) = 26
max(986..1596) = 34
max(1596..2583) = 42
max(2583..4180) = 55
max(4180..6764) = 68
[…]
The pattern is described like this at the Online Encyclopedia of Integer Sequences:
a(n) = 1 if and only if n+1 is a Fibonacci number. The length of such a quasi-period (from Fib(i)-1 to Fib(i+1)-1, inclusive) is a Fibonacci number + 1. The maximum value of a(n) within each subsequent quasi-period increases by a Fibonacci number. For example, from n = 143 to n = 232, the maximum is 13. From 232 to 376, the maximum is 16, an increase of 3. From 376 to 609, 21, an increase of 5. From 609 to 986, 26, increasing by 5 again. Each two subsequent maxima seem to increase by the same increment, the next Fibonacci number. – Kerry Mitchell, Nov 14 2009
The maxima of the quasi-periods are in A096748. – Max Barrentine, Sep 13 2015 — See commentary for A000119 at OEIS
Here is A096748:
1, 2, 2, 2, 3, 4, 5, 6, 8, 10, 13, 16, 21, 26, 34, 42, 55, 68, 89, 110, 144, 178, 233, 288, 377, 466, 610, 754, 987, 1220, 1597, 1974, 2584, 3194, 4181, 5168, 6765, 8362, 10946, 13530, 17711, 21892, 28657, 35422, 46368, 57314, 75025, 92736, 121393, 150050 — A096748, Expansion of (1+x)^2/(1-x^2-x^4), at OEIS
These maxima are the succesive highest points in a graph of A000119, Number of representations of n as a sum of distinct Fibonacci numbers:
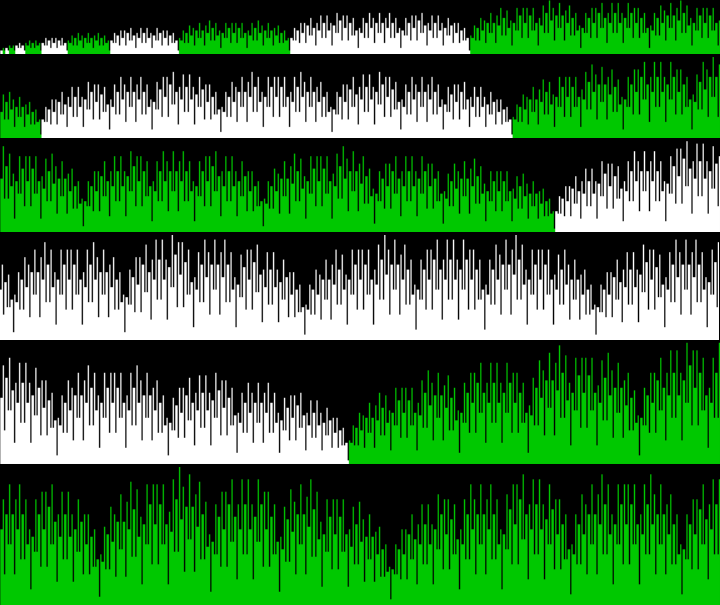
Graph of count of ways in which 1,2,3… can be sum of distinct Fibonacci numbers
The graph looks like a furry caterpillar or similar and the symmetry of counts between the 1s is more obvious there:
fibsumcounts for 33..54
fibsumcounts for 54..88
fibsumcounts for 88..143
fibsumcounts for 143..232
fibsumcounts for 232..376
fibsumcounts for 376..609
And the fractal nature of the counts is more obvious when the graph is rotated by 90° and then mirrored:
Rotated and mirrored graph of count of ways in which 1,2,3… can be sum of distinct Fibonacci numbers