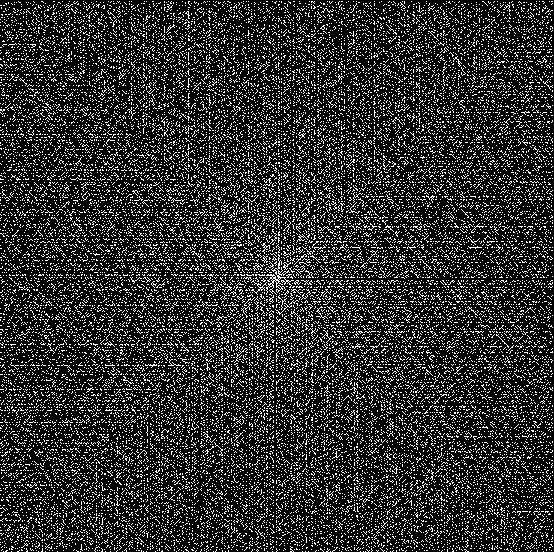Category Archives: Integer Sequences

Fabulous Furry Fibonacci Fractal

by in Arithmetic, Fibonacci Sequence, Fractals, Integer Sequences, Mathematics and tagged , , , , , , , , | Leave a comment

At least, I think it’s a fractal. I came across it when I was counting the ways in which the integers can be the sum of distinct Fibonacci numbers. Here for reference is the Fibonacci sequence, the beautiful and endlessly fertile sequence that’s seeded with “1, 1” and continued by summing the two previous numbers:

1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946, 17711, 28657, 46368, 75025, 121393, 196418, 317811, 514229, 832040…

I noticed some interesting patterns in the distinct-fib-num-sum count for the integers:

1 = 1 (count=1)
2 = 2 (count=1)
3 = 1+2 = 3 (count=2)
4 = 1+3 (c=1)
5 = 2+3 = 5 (c=2)
6 = 1+2+3 = 1+5 (c=2)
7 = 2+5 (c=1)
8 = 1+2+5 = 3+5 = 8 (c=3)
9 = 1+3+5 = 1+8 (c=2)
10 = 2+3+5 = 2+8 (c=2)
11 = 1+2+3+5 = 1+2+8 = 3+8 (c=3)
12 = 1+3+8 (c=1)
13 = 2+3+8 = 5+8 = 13 (c=3)
14 = 1+2+3+8 = 1+5+8 = 1+13 (c=3)
15 = 2+5+8 = 2+13 (c=2)
16 = 1+2+5+8 = 3+5+8 = 1+2+13 = 3+13 (c=4)
17 = 1+3+5+8 = 1+3+13 (c=2)
18 = 2+3+5+8 = 2+3+13 = 5+13 (c=3)
19 = 1+2+3+5+8 = 1+2+3+13 = 1+5+13 (c=3)
20 = 2+5+13 (c=1)
21 = 1+2+5+13 = 3+5+13 = 8+13 = 21 (c=4)
22 = 1+3+5+13 = 1+8+13 = 1+21 (c=3)
23 = 2+3+5+13 = 2+8+13 = 2+21 (c=3)
24 = 1+2+3+5+13 = 1+2+8+13 = 3+8+13 = 1+2+21 = 3+21 (c=5)
25 = 1+3+8+13 = 1+3+21 (c=2)
26 = 2+3+8+13 = 5+8+13 = 2+3+21 = 5+21 (c=4)
27 = 1+2+3+8+13 = 1+5+8+13 = 1+2+3+21 = 1+5+21 (c=4)
28 = 2+5+8+13 = 2+5+21 (c=2)
29 = 1+2+5+8+13 = 3+5+8+13 = 1+2+5+21 = 3+5+21 = 8+21 (c=5)
30 = 1+3+5+8+13 = 1+3+5+21 = 1+8+21 (c=3)
31 = 2+3+5+8+13 = 2+3+5+21 = 2+8+21 (c=3)
32 = 1+2+3+5+8+13 = 1+2+3+5+21 = 1+2+8+21 = 3+8+21 (c=4)
33 = 1+3+8+21 (c=1)
34 = 2+3+8+21 = 5+8+21 = 13+21 = 34 (c=4)
35 = 1+2+3+8+21 = 1+5+8+21 = 1+13+21 = 1+34 (c=4)
36 = 2+5+8+21 = 2+13+21 = 2+34 (c=3)
37 = 1+2+5+8+21 = 3+5+8+21 = 1+2+13+21 = 3+13+21 = 1+2+34 = 3+34
(c=6)
38 = 1+3+5+8+21 = 1+3+13+21 = 1+3+34 (c=3)
39 = 2+3+5+8+21 = 2+3+13+21 = 5+13+21 = 2+3+34 = 5+34 (c=5)
40 = 1+2+3+5+8+21 = 1+2+3+13+21 = 1+5+13+21 = 1+2+3+34 = 1+5+34
(c=5)
41 = 2+5+13+21 = 2+5+34 (c=2)
42 = 1+2+5+13+21 = 3+5+13+21 = 8+13+21 = 1+2+5+34 = 3+5+34 = 8+3
4 (c=6)
43 = 1+3+5+13+21 = 1+8+13+21 = 1+3+5+34 = 1+8+34 (c=4)
44 = 2+3+5+13+21 = 2+8+13+21 = 2+3+5+34 = 2+8+34 (c=4)
45 = 1+2+3+5+13+21 = 1+2+8+13+21 = 3+8+13+21 = 1+2+3+5+34 = 1+2+
8+34 = 3+8+34 (c=6)
46 = 1+3+8+13+21 = 1+3+8+34 (c=2)
47 = 2+3+8+13+21 = 5+8+13+21 = 2+3+8+34 = 5+8+34 = 13+34 (c=5)
48 = 1+2+3+8+13+21 = 1+5+8+13+21 = 1+2+3+8+34 = 1+5+8+34 = 1+13+
34 (c=5)
49 = 2+5+8+13+21 = 2+5+8+34 = 2+13+34 (c=3)
50 = 1+2+5+8+13+21 = 3+5+8+13+21 = 1+2+5+8+34 = 3+5+8+34 = 1+2+1
3+34 = 3+13+34 (c=6)
51 = 1+3+5+8+13+21 = 1+3+5+8+34 = 1+3+13+34 (c=3)
52 = 2+3+5+8+13+21 = 2+3+5+8+34 = 2+3+13+34 = 5+13+34 (c=4)
53 = 1+2+3+5+8+13+21 = 1+2+3+5+8+34 = 1+2+3+13+34 = 1+5+13+34 (c=4)
54 = 2+5+13+34 (c=1)
55 = 1+2+5+13+34 = 3+5+13+34 = 8+13+34 = 21+34 = 55 (c=5)
56 = 1+3+5+13+34 = 1+8+13+34 = 1+21+34 = 1+55 (c=4)

The patterns are easier to see when the counts are set out like this:

1, 1, 2, 1, 2, 2, 1, 3, 2, 2, 3, 1, 3, 3, 2, 4, 2, 3, 3, 1, 4, 3, 3, 5, 2, 4, 4, 2, 5, 3, 3, 4, 1, 4, 4, 3, 6, 3, 5, 5, 2, 6, 4, 4, 6, 2, 5, 5, 3, 6, 3, 4, 4, 1, 5, 4, 4, 7, 3, 6, 6, 3, 8, 5, 5, 7, 2, 6, 6, 4, 8, 4, 6, 6, 2, 7, 5, 5, 8, 3, 6, 6, 3, 7, 4, 4, 5, 1, 5, 5, 4, 8, 4, 7, 7, 3, 9, 6, 6, 9, 3, 8, 8, 5, 10, 5, 7, 7, 2, 8, 6, 6, 10, 4, 8, 8, 4, 10, 6, 6, 8, 2, 7, 7, 5, 10, 5, 8, 8, 3, 9, 6, 6, 9, 3, 7, 7, 4, 8, 4, 5, 5, 1, 6, 5, 5, 9, 4, 8, 8… 1… — See A000119, Number of representations of n as a sum of distinct Fibonacci numbers, at the Online Encyclopedia of Integer Sequences (OEIS)

The numbers between each pair of 1s are symmetrical:

1, 2, 1,
1, 2, 2, 1,
1, 3, 2, 2, 3, 1,
1, 3, 3, 2, 4, 2, 3, 3, 1
1, 4, 3, 3, 5, 2, 4, 4, 2, 5, 3, 3, 4, 1

And when fibsumcount(n) = 1, then n = fib(i)-1, i.e. n is one less than a Fibonacci number:

1 = 1 (c=1)
2 = 2 (c=1)
4 = 1+3 (c=1)
7 = 2+5 (c=1)
12 = 1+3+8 (c=1)
20 = 2+5+13 (c=1)
33 = 1+3+8+21 (c=1)
54 = 2+5+13+34 (c=1)
88 = 1+3+8+21+55 (c=1)
143 = 2+5+13+34+89 (c=1)
232 = 1+3+8+21+55+144 (c=1)
376 = 2+5+13+34+89+233 (c=1)
609 = 1+3+8+21+55+144+377 (c=1)
986 = 2+5+13+34+89+233+610 (c=1)
1596 = 1+3+8+21+55+144+377+987 (c=1)
2583 = 2+5+13+34+89+233+610+1597 (c=1)
4180 = 1+3+8+21+55+144+377+987+2584 (c=1)
6764 = 2+5+13+34+89+233+610+1597+4181 (c=1)
10945 = 1+3+8+21+55+144+377+987+2584+6765 (c=1)
17710 = 2+5+13+34+89+233+610+1597+4181+10946 (c=1)
[…]

I also noticed a pattern relating to the maximum count reached in the numbers between the 1s. Suppose the function max(fib(i)-1..fib(i+1)-1) returns the highest count of ways to represent the numbers from fib(i)-1 to fib(i+1)-1. Notice how max() increases:

max(2..4) = 2
max(4..7) = 2
max(7..12) = 3
max(12..20) = 4
max(20..33) = 5
max(33..54) = 6
max(54..88) = 8
max(88..143) = 10
max(143..232) = 13
max(232..376) = 16
max(376..609) = 21
max(609..986) = 26
max(986..1596) = 34
max(1596..2583) = 42
max(2583..4180) = 55
max(4180..6764) = 68
[…]

The pattern is described like this at the Online Encyclopedia of Integer Sequences:

a(n) = 1 if and only if n+1 is a Fibonacci number. The length of such a quasi-period (from Fib(i)-1 to Fib(i+1)-1, inclusive) is a Fibonacci number + 1. The maximum value of a(n) within each subsequent quasi-period increases by a Fibonacci number. For example, from n = 143 to n = 232, the maximum is 13. From 232 to 376, the maximum is 16, an increase of 3. From 376 to 609, 21, an increase of 5. From 609 to 986, 26, increasing by 5 again. Each two subsequent maxima seem to increase by the same increment, the next Fibonacci number. – Kerry Mitchell, Nov 14 2009

The maxima of the quasi-periods are in A096748. – Max Barrentine, Sep 13 2015 — See commentary for A000119 at OEIS

Here is A096748:

1, 2, 2, 2, 3, 4, 5, 6, 8, 10, 13, 16, 21, 26, 34, 42, 55, 68, 89, 110, 144, 178, 233, 288, 377, 466, 610, 754, 987, 1220, 1597, 1974, 2584, 3194, 4181, 5168, 6765, 8362, 10946, 13530, 17711, 21892, 28657, 35422, 46368, 57314, 75025, 92736, 121393, 150050 — A096748, Expansion of (1+x)^2/(1-x^2-x^4), at OEIS

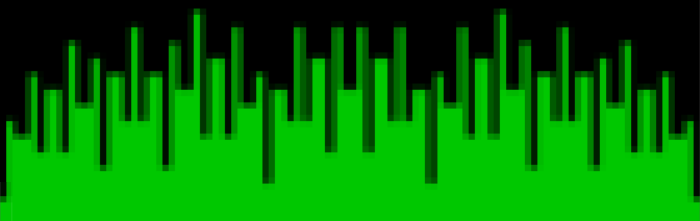
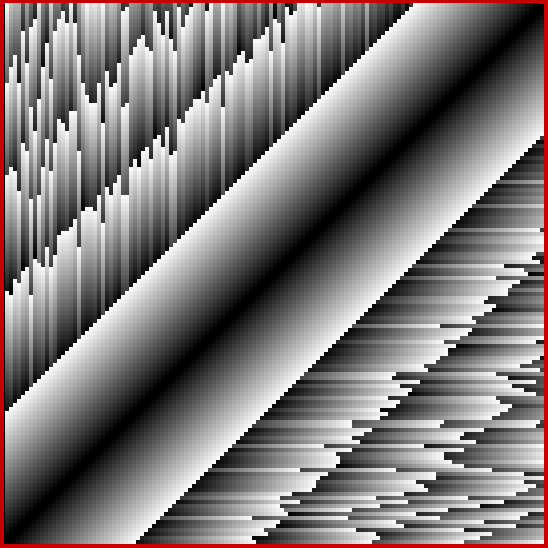
These maxima are the succesive highest points in a graph of A000119, Number of representations of n as a sum of distinct Fibonacci numbers:

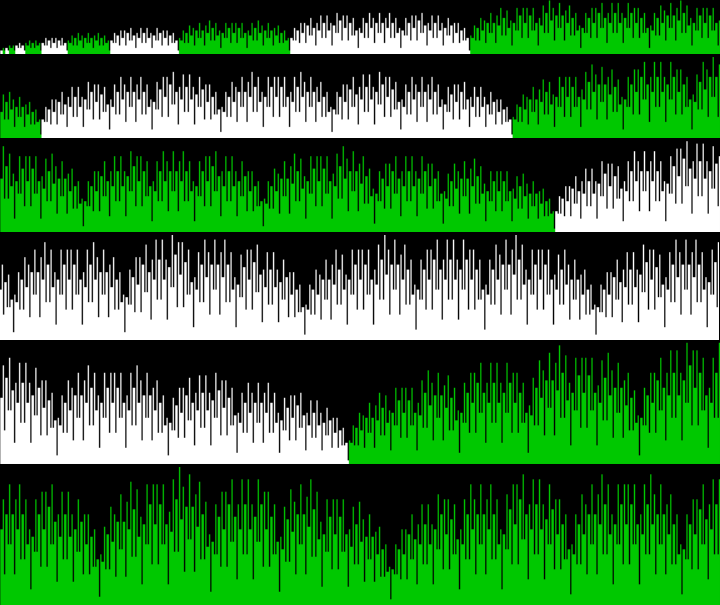
Graph of count of ways in which 1,2,3… can be sum of distinct Fibonacci numbers

The graph looks like a furry caterpillar or similar and the symmetry of counts between the 1s is more obvious there:

fibsumcounts for 33..54

fibsumcounts for 54..88

fibsumcounts for 88..143

fibsumcounts for 143..232

fibsumcounts for 232..376

fibsumcounts for 376..609

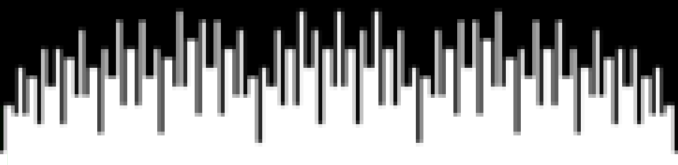
And the fractal nature of the counts is more obvious when the graph is rotated by 90° and then mirrored:

Rotated and mirrored graph of count of ways in which 1,2,3… can be sum of distinct Fibonacci numbers

Abounding in Abundants

by in Arithmetic, Integer Sequences, Mathematics, Prime numbers and tagged , , , , , , , , , , , , , , , , | Leave a comment

This is the famous Ulam spiral, invented by the Jewish mathematician Stanisław Ulam (pronounced OO-lam) to represent prime numbers on a square grid:

The Ulam spiral of prime numbers

The red square represents 1, with 2 as the white block immediately to its right and 3 immediately above 2. Then 5 is the white block one space to the left of 3 and 7 the white block one space below 5. Then 11 is the white block right beside 2 and 13 the white block one space above 11. And so on. The primes aren’t regularly spaced on the spiral but patterns are nevertheless appearing. Here’s the Ulam spiral at higher resolutions:

The Ulam spiral x2

The Ulam spiral x4

The primes are neither regular nor random in their distribution on the spiral. They stand tantalizingly betwixt and between. So the numbers represented on this Ulam-like spiral, which looks like an aerial view of a city designed by architects who occasionally get drunk:

Ulam-like spiral of abundant numbers

The distribution of abundant numbers is much more regular than the primes, but is far from wholly predictable. And what are abundant numbers? They’re numbers n such that sum(divisors(n)-n) > n. In other words, when you add the divisors of n less than n, the sum is greater than n. The first abundant number is 12:

12 is divisible by 1, 2, 3, 4, 6 → 1 + 2 + 3 + 4 + 6 = 16 > 12

The abundant numbers go like this:

12, 18, 20, 24, 30, 36, 40, 42, 48, 54, 56, 60, 66, 70, 72, 78, 80, 84, 88, 90, 96, 100, 102, 104, 108, 112, 114, 120, 126, 132, 138, 140, 144, 150, 156, 160, 162, 168, 174, 176, 180, 186, 192, 196, 198, 200, 204, 208, 210, 216, 220, 222, 224, 228, 234, 240, 246, 252, 258, 260, 264, 270… — A005101 at the Online Encyclopedia of Integer Sequences

Are all abundant numbers even? No, but the first odd abundant number takes a long time to arrive: it’s 45045. The abundance of 45045 was first discovered by the French mathematician Charles de Bovelles or Carolus Bovillus (c. 1475-1566), according to David Wells in his wonderful Penguin Dictionary of Curious and Interesting Numbers (1986):

45045 = 3^2 * 5 * 7 * 11 * 13 → 1 + 3 + 5 + 7 + 9 + 11 + 13 + 15 + 21 + 33 + 35 + 39 + 45 + 55 + 63 + 65 + 77 + 91 + 99 + 105 + 117 + 143 + 165 + 195 + 231 + 273 + 315 + 385 + 429 + 455 + 495 + 585 + 693 + 715 + 819 + 1001 + 1155 + 1287 + 1365 + 2145 + 3003 + 3465 + 4095 + 5005 + 6435 + 9009 + 15015 = 59787 > 45045

Here’s the spiral of abundant numbers at higher resolutions:

Abundant numbers x2

Abundant numbers x4

Negating the spiral of the abundant numbers — almost — is the spiral of the deficient numbers, where sum(divisors(n)-n) < n. Like most odd numbers, 15 is deficient:

15 = 3 * 5 → 1 + 3 + 5 = 9 < 15

Here’s the spiral of deficient numbers at various resolutions:

Deficient numbers on Ulam-like spiral

Deficient numbers x2

Deficient numbers x4

The spiral of deficient numbers doesn’t quite negate (reverse the colors of) the spiral of abundant numbers because of the very rare perfect numbers, where sum(divisors(n)-n) = n. That is, their factor-sums are exactly equal to themselves:

• 6 = 2 * 3 → 1 + 2 + 3 = 6
• 28 = 2^2 * 7 → 1 + 2 + 4 + 7 + 14 = 28
• 496 = 2^4 * 31 → 1 + 2 + 4 + 8 + 16 + 31 + 62 + 124 + 248 = 496

Now let’s try numbers n such than sum(divisors(n)) mod 2 = 1 (“n mod 2″ gives the remainder when n is divided by 2, i.e. n mod 2 is either 0 or 1). For example:

• 4 = 2^2 → 1 + 2 + 4 = 7 → 7 mod 2 = 1
• 18 = 2 * 3^2 → 1 + 2 + 3 + 6 + 9 + 18 = 39 → 39 mod 2 = 1
• 72 = 2^3 * 3^2 → 1 + 2 + 3 + 4 + 6 + 8 + 9 + 12 + 18 + 24 + 36 + 72 = 195 → 195 mod 2 = 1

Here are spirals for these numbers:

Ulam-like spiral for n such than sum(divisors(n)) mod 2 = 1

sum(divisors(n)) mod 2 = 1 x2

sum(divisors(n)) mod 2 = 1 x4

sum(divisors(n)) mod 2 = 1 x8

sum(divisors(n)) mod 2 = 1 x16

Pyramids for Pi

by in Arithmetic, Integer Sequences, π, Mathematics, Squares and tagged , , , , | Leave a comment

These are the odd numbers:


1, 3, 5, 7, 9, 11, 13, 15, 17, 19, 21, 23, 25, 27, 29, 31, 33, 35, 37, 39, 41, 43, 45, 47, 49, 51, 53, 55, 57, 59...

If you add the odd numbers, 1+3+5+7…, you get the square numbers:


1, 4, 9, 16, 25, 36, 49, 64, 81, 100, 121, 144, 169, 196, 225, 256, 289, 324, 361, 400, 441, 484, 529, 576, 625, 676, 729, 784, 841, 900...

And if you add the square numbers, 1+4+9+16…, you get what are called the square pyramidal numbers:


1, 5, 14, 30, 55, 91, 140, 204, 285, 385, 506, 650, 819, 1015, 1240, 1496, 1785, 2109, 2470, 2870, 3311, 3795, 4324, 4900, 5525, 6201, 6930, 7714, 8555, 9455...

There’s not a circle in sight, so you wouldn’t expect to find π amid the pyramids. But it’s there all the same. You can get π from this formula using the square pyramidal numbers:

π from a formula using square pyramidal numbers (Wikipedia)

Here are the approximations getting nearer and near to π:


3.1415926535897932384... = π
3.1666666666666666666... = sqpyra2pi(i=1) / 6 + 3
1 = sqpyra(1)

3.1415926535897932384... = π
3.1452380952380952380... = sqpyra2pi(i=3) / 6 + 3
14 = sqpyra(3)

3.1415926535897932384... = π
3.1412548236077647842... = sqpyra2pi(i=8) / 6 + 3
204 = sqpyra(8)

3.1415926535897932384... = π
3.1415189855952756236... = sqpyra2pi(i=14) / 6 + 3
1,015 = sqpyra(14)

3.1415926535897932384... = π
3.1415990074057163751... = sqpyra2pi(i=33) / 6 + 3
12,529 = sqpyra(33)

3.1415926535897932384... = π
3.1415920110950124679... = sqpyra2pi(i=72) / 6 + 3
127,020 = sqpyra(72)

3.1415926535897932384... = π
3.1415926017980070553... = sqpyra2pi(i=168) / 6 + 3
1,594,684 = sqpyra(168)

3.1415926535897932384... = π
3.1415926599504002195... = sqpyra2pi(i=339) / 6 + 3
13,043,590 = sqpyra(339)

3.1415926535897932384... = π
3.1415926530042565359... = sqpyra2pi(i=752) / 6 + 3
142,035,880 = sqpyra(752)

3.1415926535897932384... = π
3.1415926535000384883... = sqpyra2pi(i=1406) / 6 + 3
927,465,791 = sqpyra(1406)

3.1415926535897932384... = π
3.1415926535800054618... = sqpyra2pi(i=2944) / 6 + 3
8,509,683,520 = sqpyra(2944)

3.1415926535897932384... = π
3.1415926535890006043... = sqpyra2pi(i=6806) / 6 + 3
105,111,513,491 = sqpyra(6806)

3.1415926535897932384... = π
3.1415926535897000092... = sqpyra2pi(i=13892) / 6 + 3
893,758,038,910 = sqpyra(13892)

3.1415926535897932384... = π
3.1415926535897999990... = sqpyra2pi(i=33315) / 6 + 3
12,325,874,793,790 = sqpyra(33315)

3.1415926535897932384... = π
3.1415926535897939999... = sqpyra2pi(i=68985) / 6 + 3
109,433,980,000,485 = sqpyra(68985)

3.1415926535897932384... = π
3.1415926535897932999... = sqpyra2pi(i=159563) / 6 + 3
1,354,189,390,757,594 = sqpyra(159563)

3.1415926535897932384... = π
3.1415926535897932300... = sqpyra2pi(i=309132) / 6 + 3
9,847,199,658,130,890 = sqpyra(309132)

3.1415926535897932384... = π
3.1415926535897932389... = sqpyra2pi(i=774865) / 6 + 3
155,080,688,289,901,465 = sqpyra(774865)

3.1415926535897932384... = π
3.1415926535897932384... = sqpyra2pi(i=1586190) / 6 + 3
1,330,285,259,163,175,415 = sqpyra(1586190)

Summer Sets (and Truncated Triangulars)

by in Arithmetic, Integer Sequences, Mathematics, Triangular Numbers and tagged , , , | Leave a comment

Here is the sequence of triangular numbers, created by summing consecutive integers from 1 (i.e., 1+2+3+4+5…):


1, 3, 6, 10, 15, 21, 28, 36, 45, 55, 66, 78, 91, 105, 120, 136, 153, 171, 190, 210, 231, 253, 276, 300, 325, 351, 378, 406, 435, 465, 496, 528, 561, 595, 630, 666, 703, 741, 780, 820, 861, 903, 946, 990, 1035, 1081, 1128, 1176, 1225, 1275, 1326, 1378, 1431, 1485, 1540, 1596, 1653, 1711, 1770, 1830, 1891, 1953, 2016, 2080, 2145, 2211, 2278, 2346, 2415, 2485, 2556, 2628, 2701, 2775, 2850, 2926, 3003, 3081, 3160, 3240, 3321, 3403, 3486, 3570, 3655, 3741, 3828, 3916, 4005, 4095, 4186, 4278, 4371, 4465, 4560, 4656, 4753, 4851, 4950, 5050, 5151, 5253, 5356, 5460, 5565, 5671, 5778, 5886, 5995...

And here is a sequence of truncated triangulars, created by summing consecutive integers from 15 (i.e., 15+16+17+18+19…):


15, 31, 48, 66, 85, 105, 126, 148, 171, 195, 220, 246, 273, 301, 330, 360, 391, 423, 456, 490, 525, 561, 598, 636, 675, 715, 756, 798, 841, 885, 930, 976, 1023, 1071, 1120, 1170, 1221, 1273, 1326, 1380, 1435, 1491, 1548, 1606, 1665, 1725, 1786, 1848, 1911, 1975, 2040, 2106, 2173, 2241, 2310, 2380, 2451, 2523, 2596, 2670, 2745, 2821, 2898, 2976, 3055, 3135, 3216, 3298, 3381, 3465, 3550, 3636, 3723, 3811, 3900, 3990, 4081, 4173, 4266, 4360, 4455, 4551, 4648, 4746, 4845, 4945, 5046, 5148, 5251, 5355, 5460, 5566, 5673, 5781...

It’s obvious that the sequences are different at each successive step: 1 ≠ 15, 3 ≠ 31, 6 ≠ 48, 10 ≠ 66, 21 ≠ 85, and so on. But seven numbers occur in both sequences: 15, 66, 105, 171, 561, 1326 and 5460. And that’s it — 7 is the 14-th entry in A309507 at the Encyclopedia of Integer Sequences:


0, 1, 1, 1, 3, 3, 1, 2, 5, 3, 3, 3, 3, 7, 3, 1, 5, 5, 3, 7, 7, 3, 3, 5, 5, 7, 7, 3, 7, 7, 1, 3, 7, 7, 11, 5, 3, 7, 7, 3, 7, 7, 3, 11, 11, 3, 3, 5, 8, 11, 7, 3, 7, 15, 7, 7, 7, 3, 7, 7, 3, 11, 5, 3, 15, 7, 3, 7, 15, 7, 5, 5, 3, 11, 11, 7, 15, 7, 3, 9, 9, 3, 7 — A309507

I decided to take create graphs of shared numbers in compared sequences like this. In the 135×135 grid below, the brightness of the squares corresponds to the count of shared numbers in the sequence-pair sum(x..x+n) and sum(y..y+n), where x and y are the coordinates of each individual square. I think the grid looks like a city of skyscrapers bisected by a highway:

Count of shared numbers in sequence-pairs sum(x..x+n) and sum(y..y+n)

Note that the bright white diagonal in the grid corresponds to the sequence-pairs where x = y. Because the sequences are identical in each pair, the count of shared numbers is infinite. The grid is symmetrically reflected along the diagonal because, for example, the sequence-pair for x=12, y=43, where sum(12..12+n) is compared with sum(43..43+n), corresponds to the sequence pair for x=43, y=12, where sum(43..43+n) is compared with sum(12..12+n). The scale of brightness runs from 0 (black) to 255 (full white) and increases by 32 for each shared number in the sequence. Obviously, then, the brightness can’t increase indefinitely and some maximally bright squares will represent sequence-pairs that have different counts of shared pairs.

Now try altering the size of the step in brightness. You get grids in which the width of the central strip increases (smaller step) or decreases (bigger step). Here are grids for steps for 1, 2, 4, 8, 16, 32 and 64 (I’ve removed the bright x=y diagonal for the first few grids, because it’s too prominent against duller shades):

Brightness-step = 1

Brightness-step = 2

Brightness-step = 4

Brightness-step = 8

Brightness-step = 16

Brightness-step = 32

Brightness-step = 63

Brightness-step = 1, 2, 4, 8, 16, 32, 63 (animated)

Power Flip

by in Arithmetic, Base Behavior, Integer Sequences, Mathematics, Powers, Prime numbers and tagged , , , , , , , , , , , , , , | Leave a comment

12 is an interesting number in a lot of ways. Here’s one way I haven’t seen mentioned before:

12 = 3^1 * 2^2


The digits of 12 represent the powers of the primes in its factorization, if primes are represented from right-to-left, like this: …7, 5, 3, 2. But I couldn’t find any more numbers like that in base 10, so I tried a power flip, from right-left to left-right. If the digits from left-to-right represent the primes in the order 2, 3, 5, 7…, then this number is has prime-power digits too:

81312000 = 2^8 * 3^1 * 5^3 * 7^1 * 11^2 * 13^0 * 17^0 * 19^0


Or, more simply, given that n^0 = 1:

81312000 = 2^8 * 3^1 * 5^3 * 7^1 * 11^2


I haven’t found any more left-to-right prime-power digital numbers in base 10, but there are more in other bases. Base 5 yields at least three (I’ve ignored numbers with just two digits in a particular base):

110 in b2 = 2^1 * 3^1 (n=6)
130 in b6 = 2^1 * 3^3 (n=54)
1010 in b2 = 2^1 * 3^0 * 5^1 (n=10)
101 in b3 = 2^1 * 3^0 * 5^1 (n=10)
202 in b7 = 2^2 * 3^0 * 5^2 (n=100)
3020 in b4 = 2^3 * 3^0 * 5^2 (n=200)
330 in b8 = 2^3 * 3^3 (n=216)
13310 in b14 = 2^1 * 3^3 * 5^3 * 7^1 (n=47250)
3032000 in b5 = 2^3 * 3^0 * 5^3 * 7^2 (n=49000)
21302000 in b5 = 2^2 * 3^1 * 5^3 * 7^0 * 11^2 (n=181500)
7810000 in b9 = 2^7 * 3^8 * 5^1 (n=4199040)
81312000 in b10 = 2^8 * 3^1 * 5^3 * 7^1 * 11^2


Post-Performative Post-Scriptum

When I searched for 81312000 at the Online Encyclopedia of Integer Sequences, I discovered that these are Meertens numbers, defined at A246532 as the “base n Godel encoding of x [namely,] 2^d(1) * 3^d(2) * … * prime(k)^d(k), where d(1)d(2)…d(k) is the base n representation of x.”

Spiral Artefact #2

by in Arithmetic, Integer Sequences, Mathematics, Ulam Spirals and tagged , , , , , , , , , | Leave a comment

Why stop at primes? Those are the numbers the Ulam spiral is usually used for. You get a grid of square blocks, then move outward from the middle of the grid in a spiral, counting as you go. If the count matches a prime, you fill the block in. The first block is 1. Not filled. The second block is 2, which is prime. So the block is filled. The third block is 3, which is prime. Filled again. And so on. In the end, the Ulam spiral for primes looks like this:

The Ulam spiral of prime numbers

But why stop at primes? If you change the fill-test, you get different patterns. I’ve recently tried a test based on how many ways a number can be represented as the sum of consecutive integers. For example, 5, 208 and 536 can be represented in only one way:

5 = 2+3
208 = 10 + 11 + 12 + 13 + 14 + 15 + 16 + 17 + 18 + 19 + 20 + 21 + 22
536 = sum(26..41) = 26 + 27 + 28 + 29 + 30 + 31 + 32 + 33 + 34 + 35 + 36 + 37 + 38 + 39 + 40 + 41

Let’s use “runsum” to mean a sum of consecutive integers. If the function runsum(n) returns the count of runsums for n, then runsum(5) = runsum(208) = runsum(536) = 1. Here are spirals for runsum(n) = 1:

A spiral for runsum(n) = 1, i.e. numbers that are the sum of consecutive integers in only one way

runsum(n) = 1 (higher resolution)

runsum(n) = 1 (higher resolution still)

Now try runsum(n) = 2, i.e. numbers that are the sum of consecutive integers in exactly two ways:

A spiral for runsum(n) = 2

runsum(n) = 2 (hi-res #1)

runsum(n) = 2 (hi-res #2)

runsum(n) = 2 (hi-res #3)

Why do most of the numbers fall on a diagonal? I don’t know, but I know that the diagonal represents square numbers:

9 = sum(4..5) = sum(2..4)
25 = sum(12..13) = sum(3..7)
36 = sum(11..13) = sum(1..8)
49 = sum(24..25) = sum(4..10)

Now try runsum(n) = 3:

A spiral for runsum(n) = 3

runsum(n) = 3 (hi-res)

It’s a densely packed spiral, unlike the spiral for runsum(n) = 4:

A spiral for runsum(n) = 4

runsum(n) = 4 (hi-res)

Like the spiral for runsum(n) = 2, the numbers are disproportionately falling on the diagonal of square numbers:

81 = 9^2 = sum(40..41) = sum(26..28) = sum(11..16) = sum(5..13)
324 = 18^2 = sum(107..109) = sum(37..44) = sum(32..40) = sum(2..25)
2500 = 50^2 = sum(498..502) = sum(309..316) = sum(88..112) = sum(43..82)

Here are spirals for runsum(n) = 5:

A spiral for runsum(n) = 5 (note patterns in green)

runsum(n) = 5 (hi-res #1)

runsum(n) = 5 (hi-res #2)

There are two interesting patterns in the spiral, marked in green above and enlarged below:

Pattern #1 in spiral for runsum(n) = 5

Pattern #2 in spiral for runsum(n) = 5

Are the patterns merely artefacts or does one or both represent something mathematically significant? I don’t know.

More spirals:

A spiral for runsum(n) = 6

A spiral for runsum(n) = 7

runsum(n) = 7 (hi-res)

A spiral for runsum(n) = 8

runsum(n) = 8 (hi-res #1)

runsum(n) = 8 (hi-res #2)

Numbers in the spiral for runsum(n) = 8 are again falling disproportionately on the diagonal of square numbers. Here’s one of those squares:

441 = 21^2 = sum(220..221) = sum(146..148) = sum(71..76) = sum(60..66) = sum(45..53) = sum(25..38) = sum(16..33) = sum(11..31)

Previously Pre-Posted…

• Spiral Artefact #1 — a look at patterns in spirals with different tests

Nexcelsior

by in Integer Sequences, Mathematics, Triangular Numbers and tagged , , , , | Leave a comment

In “The Trivial Troot”, I looked at what happens when tri(k), the k-th triangular number, is one digit longer than the previous triangular number, tri(k-1):


6 = tri(3)
10 = tri(4)

91 = tri(13)
105 = tri(14)

990 = tri(44)
1035 = tri(45)
[...]

↓

10 ← 4
105 ← 14
1035 ← 45
10011 ← 141
100128 ← 447
1000405 ← 1414
10001628 ← 4472
100005153 ← 14142
1000006281 ← 44721
10000020331 ← 141421
100000404505 ← 447214
1000001326005 ← 1414214
10000002437316 ← 4472136
100000012392316 ← 14142136
[...]

What’s going on with k? In a sense, it’s calculating the square roots of 2 and 20:

√2 = 1·414213562373095048801688724209698078569671875376948073176679738...
√20 = 4·472135954999579392818347337462552470881236719223051448541794491...

Now let’s say “Excelsior!” and go higher with a related sequence. A006003 is defined at the Online Encyclopedia of Integer Sequences as the “sum of the next n natural numbers”. Here it is:


1 = 1
5 = 2 + 3
15 = 4 + 5 + 6
34 = 7 + 8 + 9 + 10
65 = 11 + 12 + 13 + 14 + 15
111 = 16 + 17 + 18 + 19 + 20 + 21
175 = 22 + 23 + 24 + 25 + 26 + 27 + 28
260 = 29 + 30 + 31 + 32 + 33 + 34 + 35 + 36
369 = 37 + 38 + 39 + 40 + 41 + 42 + 43 + 44 + 45
505 = 46 + 47 + 48 + 49 + 50 + 51 + 52 + 53 + 54 + 55
671 = 56 + 57 + 58 + 59 + 60 + 61 + 62 + 63 + 64 + 65 + 66
870 = 67 + 68 + 69 + 70 + 71 + 72 + 73 + 74 + 75 + 76 + 77 + 78
1105 = 79 + 80 + 81 + 82 + 83 + 84 + 85 + 86 + 87 + 88 + 89 + 90 + 91
1379 = 92 + 93 + 94 + 95 + 96 + 97 + 98 + 99 + 100 + 101 + 102 + 103 + 104 + 105
1695 = 106 + 107 + 108 + 109 + 110 + 111 + 112 + 113 + 114 + 115 + 116 + 117 + 118 + 119 + 120
2056 = 121 + 122 + 123 + 124 + 125 + 126 + 127 + 128 + 129 + 130 + 131 + 132 + 133 + 134 + 135 + 136
2465 = 137 + 138 + 139 + 140 + 141 + 142 + 143 + 144 + 145 + 146 + 147 + 148 + 149 + 150 + 151 + 152 + 153
2925 = 154 + 155 + 156 + 157 + 158 + 159 + 160 + 161 + 162 + 163 + 164 + 165 + 166 + 167 + 168 + 169 + 170 + 171
3439 = 172 + 173 + 174 + 175 + 176 + 177 + 178 + 179 + 180 + 181 + 182 + 183 + 184 + 185 + 186 + 187 + 188 + 189 + 190
4010 = 191 + 192 + 193 + 194 + 195 + 196 + 197 + 198 + 199 + 200 + 201 + 202 + 203 + 204 + 205 + 206 + 207 + 208 + 209 + 210
[...]

If you’re familiar with triangular numbers, you’ll see that sumnext(k) is always higher than tri(k), except for sumnext(1) = 1 = tri(k). Now, this is what happens when sumnext(k) is one digit longer than sumnext(k-1):


5 = sumnext(2)
15 = sumnext(3)

65 = sumnext(5)
111 = sumnext(6)

870 ← 12
1105 ← 13

9855 ← 27
10990 ← 28

97585 ← 58
102719 ← 59

976625 ← 125
1000251 ← 126

9951391 ← 271
10061960 ← 272

99588644 ← 584
100101105 ← 585

997809119 ← 1259
1000188630 ← 1260

9995386529 ← 2714
10006439295 ← 2715
[...]

↓

15 ← 3
111 ← 6
1105 ← 13
10990 ← 28
102719 ← 59
1000251 ← 126
10061960 ← 272
100101105 ← 585
1000188630 ← 1260
10006439295 ← 2715
100049490449 ← 5849
1000188006300 ← 12600
10000910550385 ← 27145
100003310078561 ← 58481
1000021311323825 ← 125993
10000026341777165 ← 271442
100000232056567634 ← 584804
1000002262299152685 ← 1259922
10000004237431278525 ← 2714418
100000026858987459346 ← 5848036
1000000119305407615071 ← 12599211
10000000921801015908705 ← 27144177
100000001209342964609615 ← 58480355
1000000000250317736274865 ← 125992105
10000000037633414521952245 ← 271441762
100000000183357362892853070 ← 584803548
1000000000250317673908773025 ← 1259921050
[...]

What’s going on now? In a sense, the digits of k are approximating the cube roots of 20, 200 and 2000:


2.714417616594906571518089469679489204805107769489096957284365443... = cuberoot(20)
5.848035476425732131013574720275845557060997270202060082845147020... = cuberoot(200)
12.59921049894873164767210607278228350570251464701507980081975112... = cuberoot(2000)

cuberoot(20) = 2.714417616594906571518089469679489204805107769489096957284365443...
cuberoot(200) = 5.848035476425732131013574720275845557060997270202060082845147020...
cuberoot(2000) = 12.59921049894873164767210607278228350570251464701507980081975112...

So you could say that this sequence has gone nexcelsior: sumnext(k) > tri(k); cubes are higher than squares; and (20, 200, 2000) is bigger than (2, 20).

Previously Pre-Posted…

• “The Trivial Troot” — explaining the earlier pattern in triangular numbers

Grow Fourth

by in Arithmetic, Integer Sequences, Mathematics, Powers and tagged , , , , , , , , , , | Leave a comment

Write the integers in groups of one, two, three, four… numbers like this:

1, 2,3, 4,5,6, 7,8,9,10, 11,12,13,14,15, 16,17,18,19,20,21, 22,23,24,25,26,27,28, 29,30,31,32,33,34,35,36, 37,38,39,40,41,42,43,44,45, 46,47,48,49,50,51,52,53,54,55, 56,57,58,59,60,61,62,63,64,65,66…

Now delete every second group:

1, 2,3, 4,5,6, 7,8,9,10, 11,12,13,14,15, 16,17,18,19,20,21, 22,23,24,25,26,27,28, 29,30,31,32,33,34,35,36, 37,38,39,40,41,42,43,44,45, 46,47,48,49,50,51,52,53,54,55, 56,57,58,59,60,61,62,63,64,65,66…

↓↓↓

1, 4,5,6, 11,12,13,14,15, 22,23,24,25,26,27,28, 37,38,39,40,41,42,43,44,45, 56,57,58,59,60,61,62,63,64,65,66…

The sum of the first n remaining groups equals n^4:

1 = 1 = 1^4

1 + 4+5+6 = 16 = 2^4

1 + 4+5+6 + 11+12+13+14+15 = 81 = 3^4

1 + 4+5+6 + 11+12+13+14+15 + 22+23+24+25+26+27+28 = 256 = 4^4

1 + 4+5+6 + 11+12+13+14+15 + 22+23+24+25+26+27+28 + 37+38+39+40+41+42+43+44+45 = 625 = 5^4

1 + 4+5+6 + 11+12+13+14+15 + 22+23+24+25+26+27+28 + 37+38+39+40+41+42+43+44+45 + 56+57+58+59+60+61+62+63+64+65+66 = 1296 = 6^4

1 + 4+5+6 + 11+12+13+14+15 + 22+23+24+25+26+27+28 + 37+38+39+40+41+42+43+44+45 + 56+57+58+59+60+61+62+63+64+65+66 + 79+80+81+82+83+84+85+86+87+88+89+90+91 = 2401 = 7^4

1 + 4+5+6 + 11+12+13+14+15 + 22+23+24+25+26+27+28 + 37+38+39+40+41+42+43+44+45 + 56+57+58+59+60+61+62+63+64+65+66 + 79+80+81+82+83+84+85+86+87+88+89+90+91 + 106+107+108+109+110+111+112+113+114+115+116+117+118+119+120 = 4096 = 8^4

1 + 4+5+6 + 11+12+13+14+15 + 22+23+24+25+26+27+28 + 37+38+39+40+41+42+43+44+45 + 56+57+58+59+60+61+62+63+64+65+66 + 79+80+81+82+83+84+85+86+87+88+89+90+91 + 106+107+108+109+110+111+112+113+114+115+116+117+118+119+120 + 137+138+139+140+141+142+143+144+145+146+147+148+149+150+151+152+153 = 6561 = 9^4

From David Wells’ Penguin Dictionary of Curious and Interesting Numbers (1986), entry for “81”

Pyramidic Palindromes

by in Base Behavior, Integer Sequences, π, Mathematics, Palindromic numbers, Pi, Powers, Squares and tagged , , , , , , , , , , , | Leave a comment

As I’ve said before on Overlord of the Über-Feral: squares are boring. As I’ve shown before on Overlord of the Über-Feral: squares are not so boring after all.

Take A000330 at the Online Encyclopedia of Integer Sequences:

1, 5, 14, 30, 55, 91, 140, 204, 285, 385, 506, 650, 819, 1015, 1240, 1496, 1785, 2109, 2470, 2870, 3311, 3795, 4324, 4900, 5525, 6201, 6930, 7714, 8555, 9455, 10416, 11440, 12529, 13685, 14910, 16206, 17575, 19019, 20540, 22140, 23821, 25585, 27434, 29370… — A000330 at OEIS

The sequence shows the square pyramidal numbers, formed by summing the squares of integers:

• 1 = 1^2
• 5 = 1^2 + 2^2 = 1 + 4
• 14 = 1^2 + 2^2 + 3^2 = 1 + 4 + 9
• 30 = 1^2 + 2^2 + 3^2 + 4^2 = 1 + 4 + 9 + 16

[…]

You can see the pyramidality of the square pyramidals when you pile up oranges or cannonballs:

Square pyramid of 91 cannonballs at Rye Castle, East Sussex (Wikipedia)

I looked for palindromes in the square pyramidals. These are the only ones I could find:

1 (k=1)
5 (k=2)
55 (k=5)
1992991 (k=181)

The only ones in base 10, that is. When I looked in base 9 = 3^2, I got a burst of pyramidic palindromes like this:

1 (k=1)
5 (k=2)
33 (k=4) = 30 in base 10 (k=4)
111 (k=6) = 91 in b10 (k=6)
122221 (k=66) = 73810 in b10 (k=60)
123333321 (k=666) = 54406261 in b10 (k=546)
123444444321 (k=6,666) = 39710600020 in b10 (k=4920)
123455555554321 (k=66,666) = 28952950120831 in b10 (k=44286)
123456666666654321 (k=666,666) = 21107018371978630 in b10 (k=398580)
123456777777777654321 (k=6,666,666) = 15387042129569911801 in b10 (k=3587226)
123456788888888887654321 (k=66,666,666) = 11217155797104231969640 in b10 (k=32285040)

The palindromic pattern from 6[…]6 ends with 66,666,666, because 8 is the highest digit in base 9. When you look at the 666,666,666th square pyramidal in base 9, you’ll find it’s not a perfect palindrome:

123456801111111111087654321 (k=666,666,666) = 8177306744945450299267171 in b10 (k=290565366)

But the pattern of pyramidic palindromes is good while it lasts. I can’t find any other base yielding a pattern like that. And base 9 yields another burst of pyramidic palindromes in a related sequence, A000537 at the OEIS:

1, 9, 36, 100, 225, 441, 784, 1296, 2025, 3025, 4356, 6084, 8281, 11025, 14400, 18496, 23409, 29241, 36100, 44100, 53361, 64009, 76176, 90000, 105625, 123201, 142884, 164836, 189225, 216225, 246016, 278784, 314721, 354025, 396900, 443556, 494209, 549081… — A000537 at OEIS

The sequence is what you might call the cubic pyramidal numbers, that is, the sum of the cubes of integers:

• 1 = 1^2
• 9 = 1^2 + 2^3 = 1 + 8
• 36 = 1^3 + 2^3 + 3^3 = 1 + 8 + 27
• 100 = 1^3 + 2^3 + 3^3 + 4^3 = 1 + 8 + 27 + 64

[…]

I looked for palindromes there in base 9:

1 (k=1) = 1 (k=1)
121 (k=4) = 100 in base 10 (k=4)
12321 (k=14) = 8281 (k=13)
1234321 (k=44) = 672400 (k=40)
123454321 (k=144) = 54479161 (k=121)
12345654321 (k=444) = 4412944900 (k=364)
1234567654321 (k=1444) = 357449732641 (k=1093)
123456787654321 (k=4444) = 28953439105600 (k=3280)
102012022050220210201 (k=137227) = 12460125198224404009 (k=84022)

But while palindromes are fun, they’re not usually mathematically significant. However, this result using the square pyrmidals is certainly significant:

Previously Pre-Posted…

More posts about how squares aren’t so boring after all:

• Curvous Energy
• Back to Drac #1
• Back to Drac #2
• Square’s Flair