Category Archives: Triangles

Squaring the Triangle

by in Circles, Fractals, Geometry, Mathematics, Sierpiński triangle, Triangles and tagged , , , , , | Leave a comment

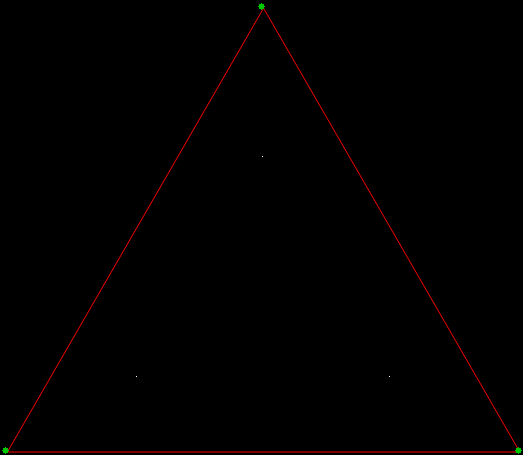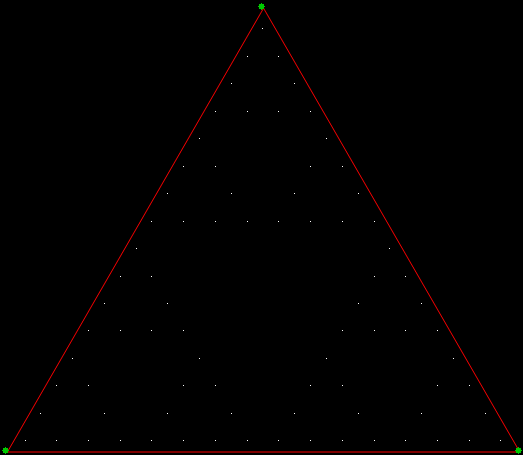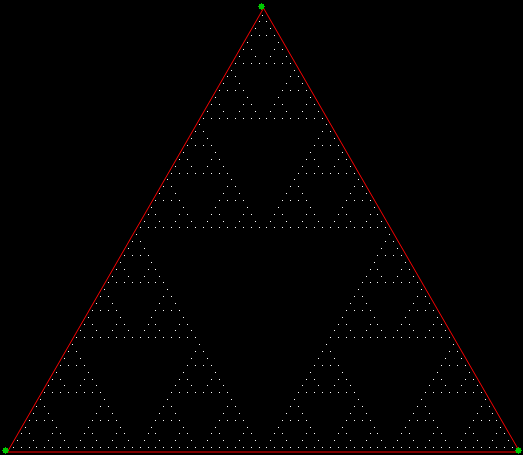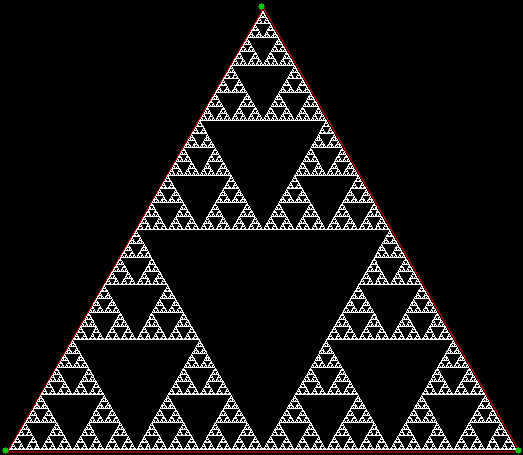
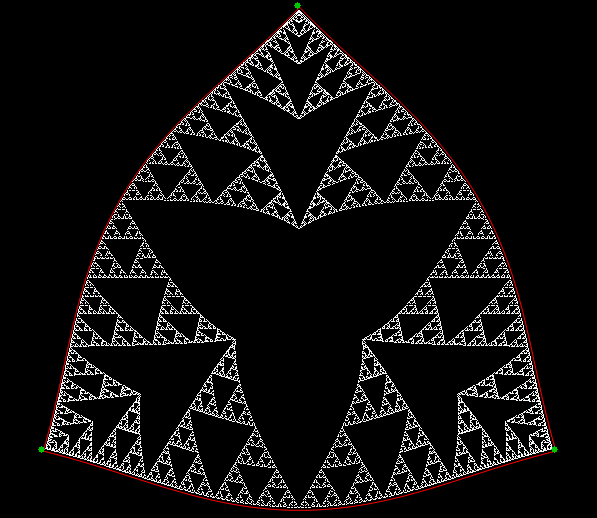
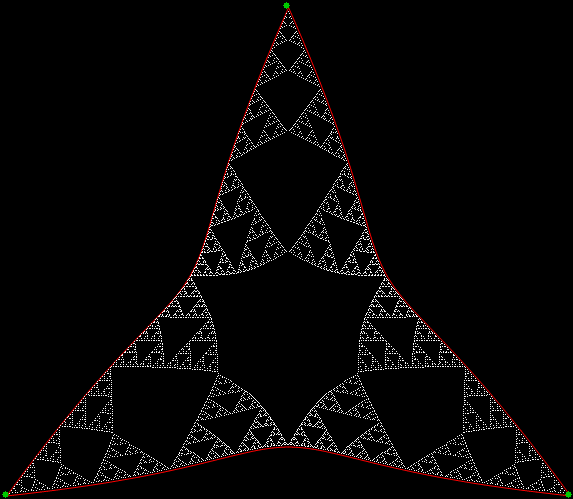
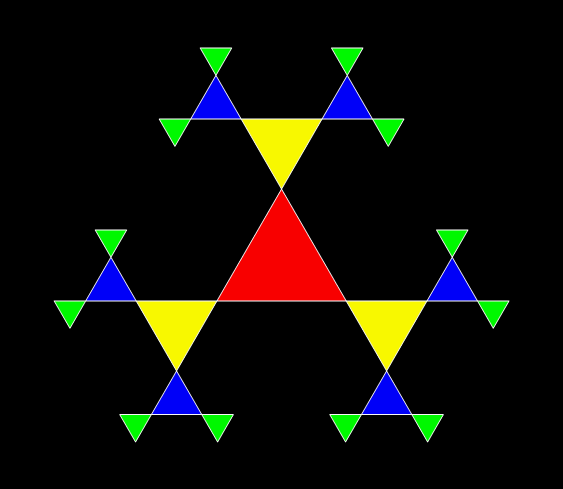
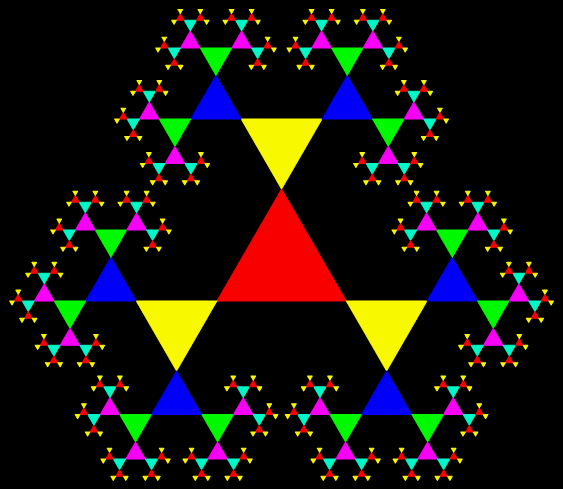
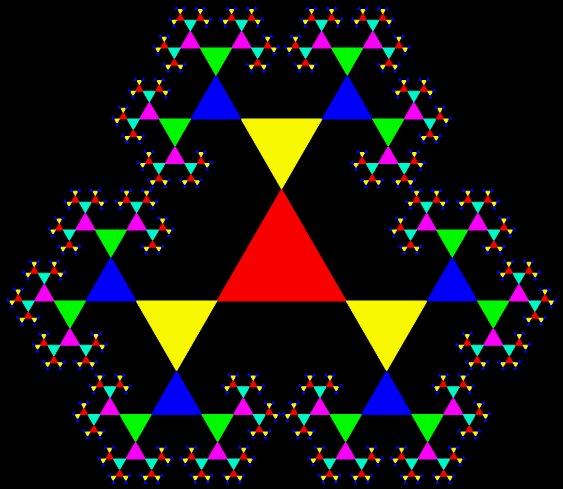
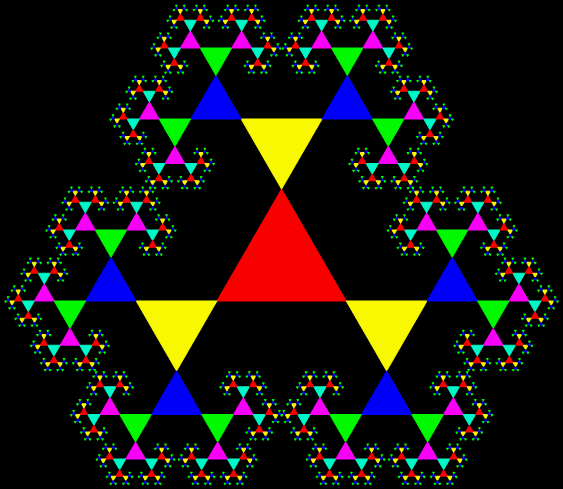
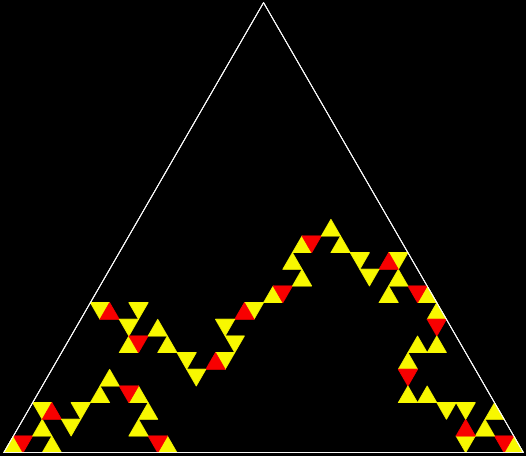
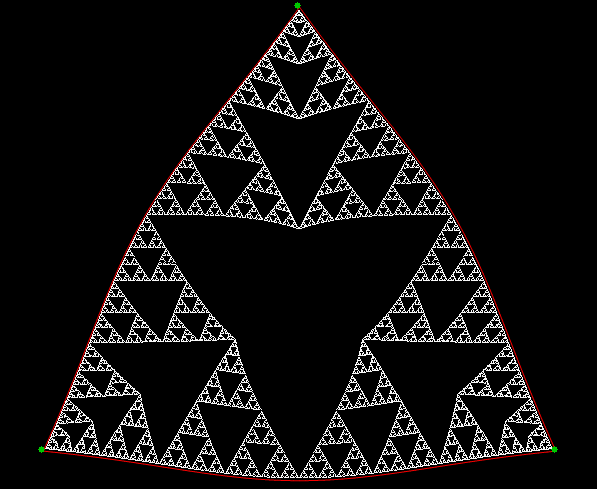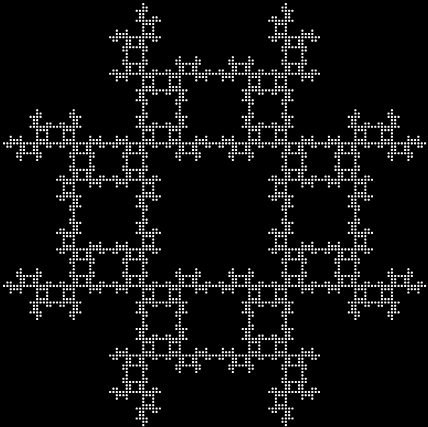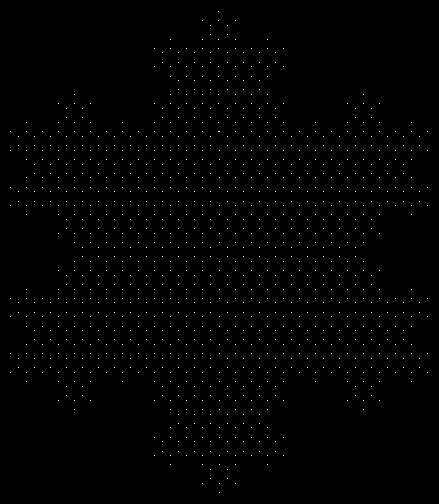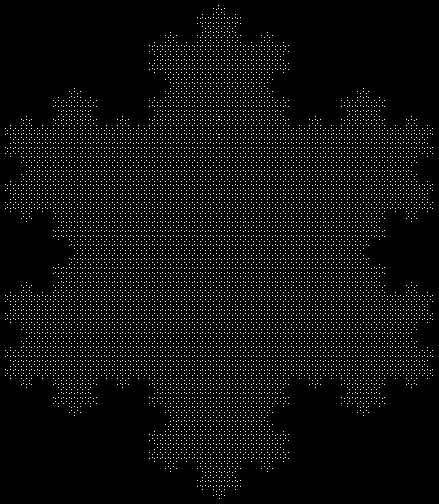It’s an interesting little exercise in elementary trigonometry to turn the Sierpiński triangle…

A Sierpiński triangle

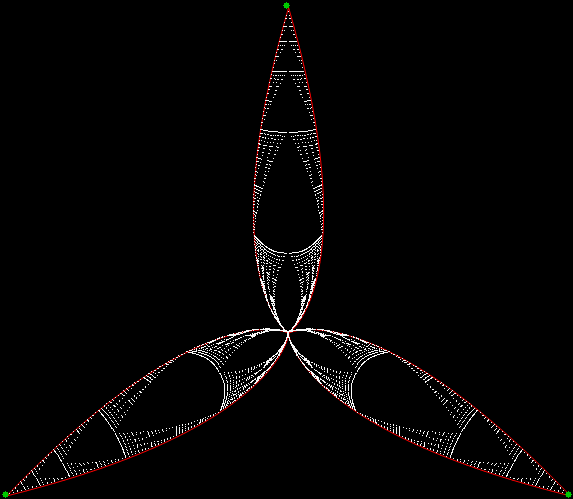
…into its circular equivalent:

A Sierpiński trisc

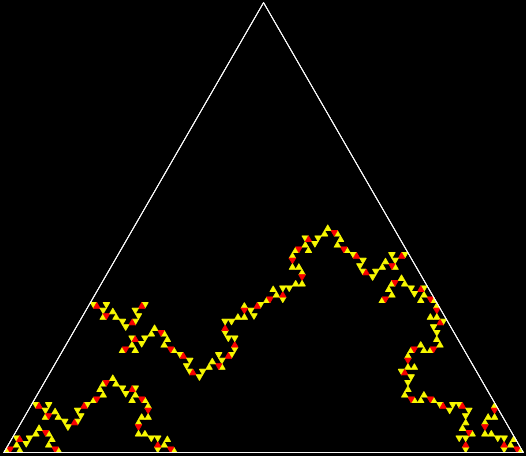
You could call that a trisc, because it’s a triangle turned into a disc. And here’s triangle-and-trisc in one image:

Sierpiński triangle + Sierpiński trisc

But what’s the square equivalent of a Sierpiński triangle? This is:

Square from Sierpiński triangle

You can do that directly, as it were:

Sierpiński triangle → square

Or you can convert the triangle into a disc, then the disc into a square, like this:

Sierpiński triangle → trisc → square

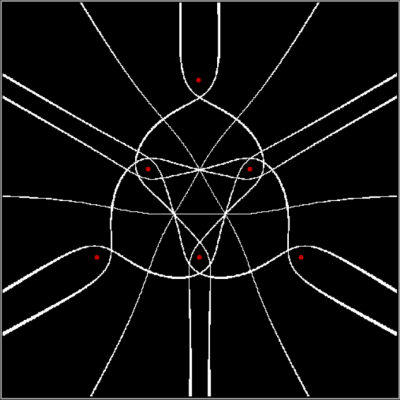
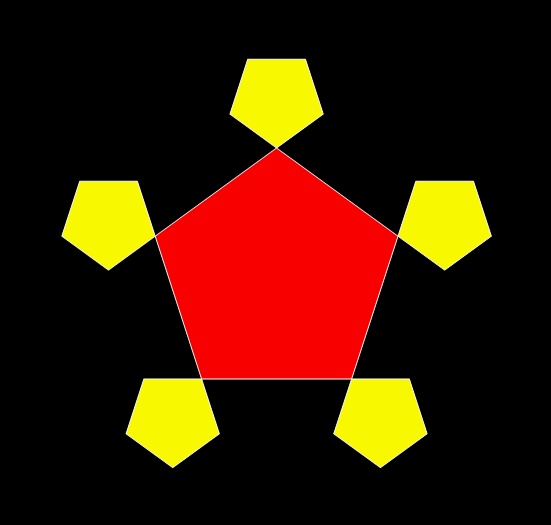
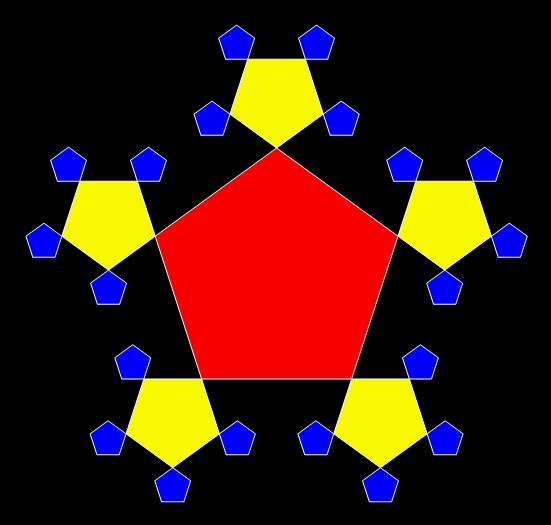
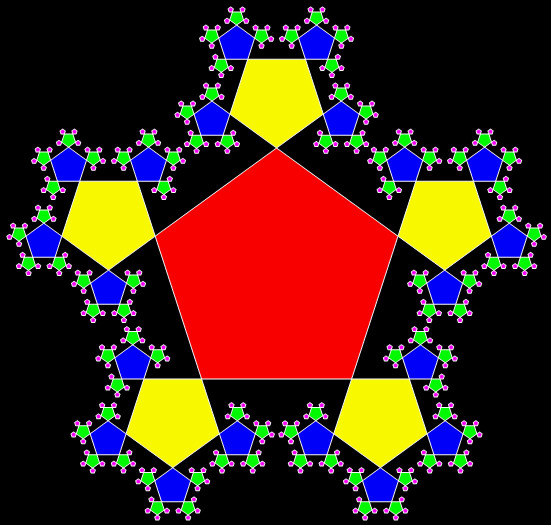
Now try converting the triangle into a pentagon:

Pentagon from Sierpiński triangle

Sierpiński triangle → pentagon

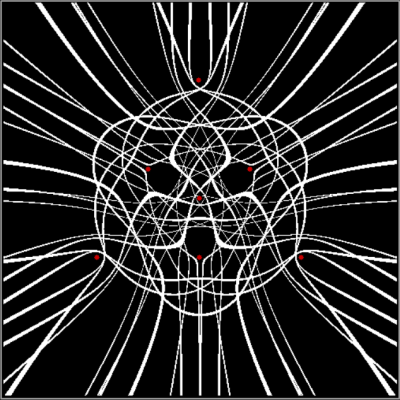
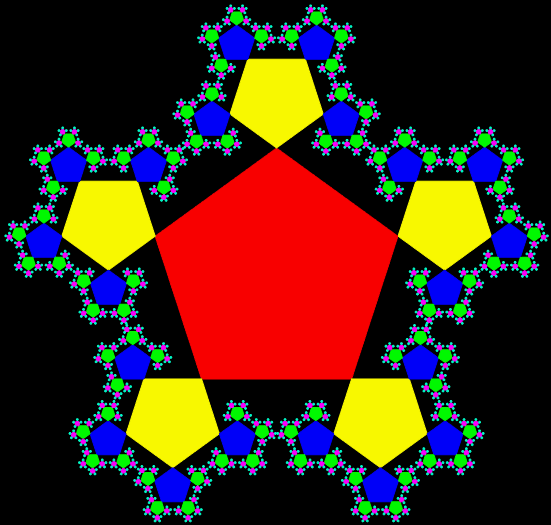
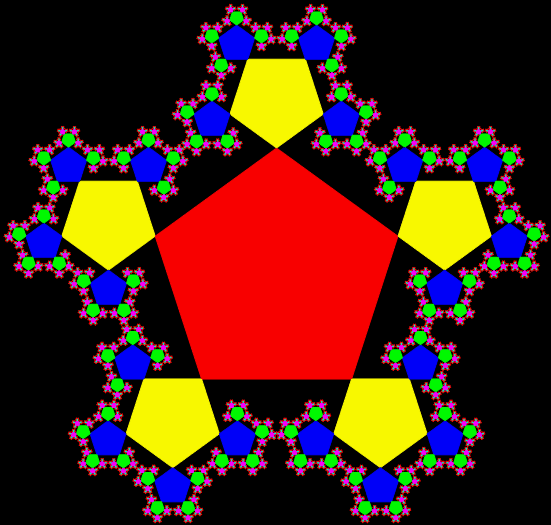
Sierpiński triangle → trisc → pentagon

And a hexagon:

Hexagon from Sierpiński triangle

Sierpiński triangle → hexagon

Sierpiński triangle → trisc → hexagon

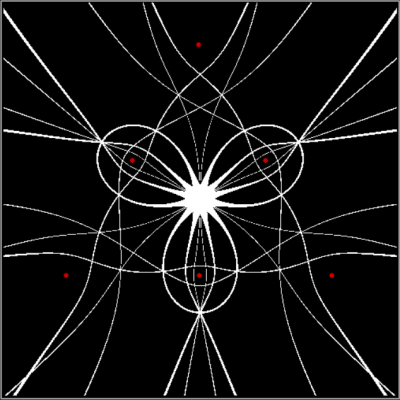
But you can also convert the Sierpiński trisc back into a Sierpiński triangle, then into a Sierpiński trisc again:

Sierpiński triangle → trisc → triangle → trisc

Sierpiński triangle → trisc → triangle → trisc (animated at Ezgif)

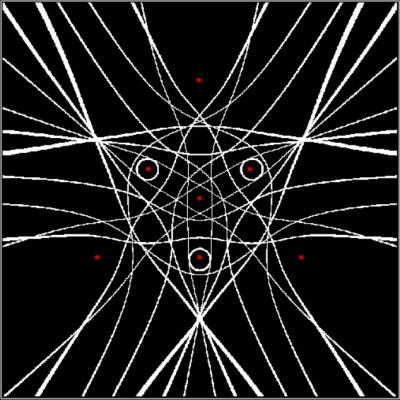
Sierpiński triangle → trisc → triangle → trisc (b&w)

Sierpiński triangle → trisc → triangle → trisc (b&w) (animated at Ezgif)

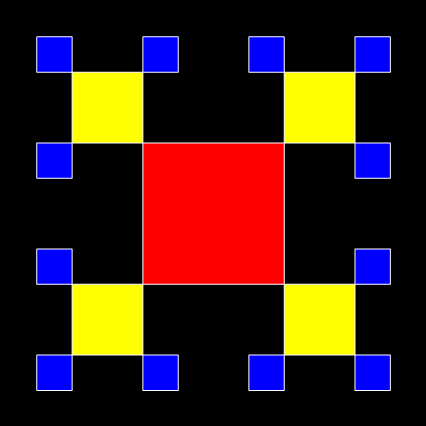
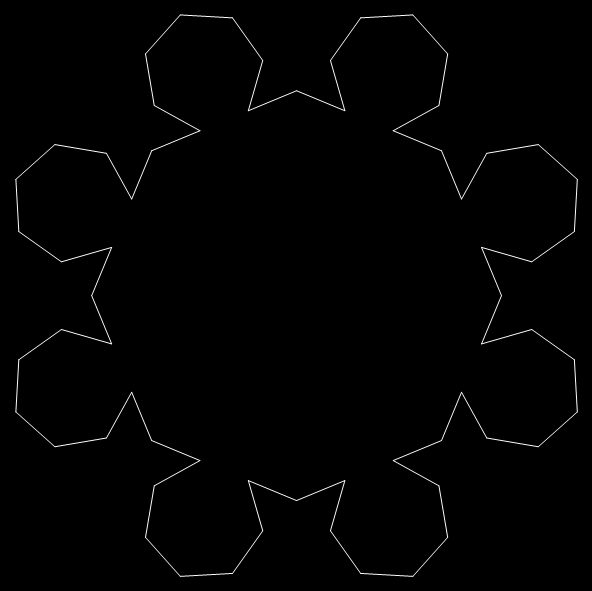
After triangles come squares. Here’s a shape called a T-square fractal:

T-square fractal

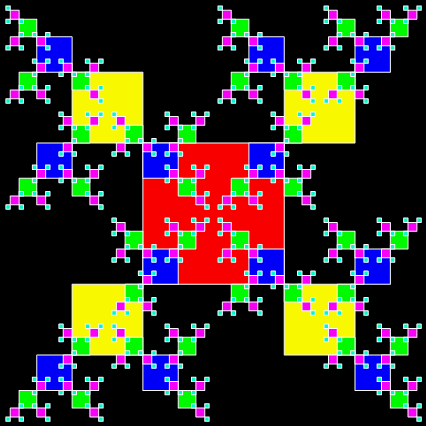
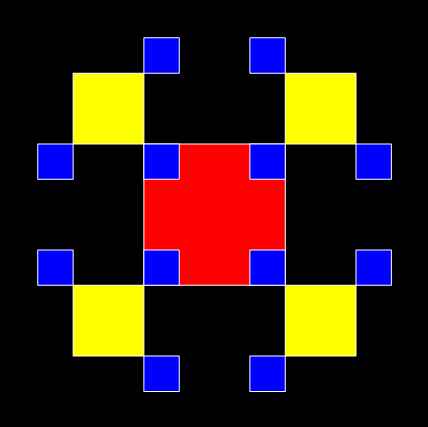
And here’s the circular equivalent of a T-square fractal:

T-square fractal → T-squisc

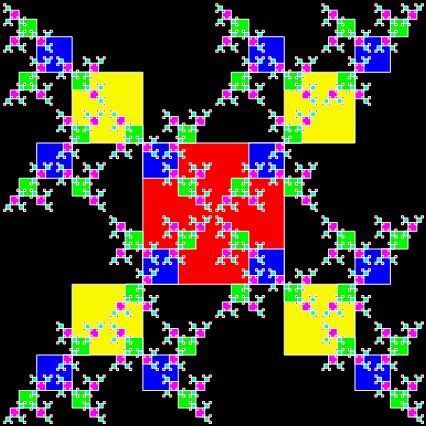
T-square fractal + T-squisc

If a disc from a triangle is a trisc, then a disc from a square is a squisc (it would be pentisc, hexisc, heptisc for pentagonal, hexagonal and heptagonal fractals). Here’s the octagonal equivalent of a T-square fractal:

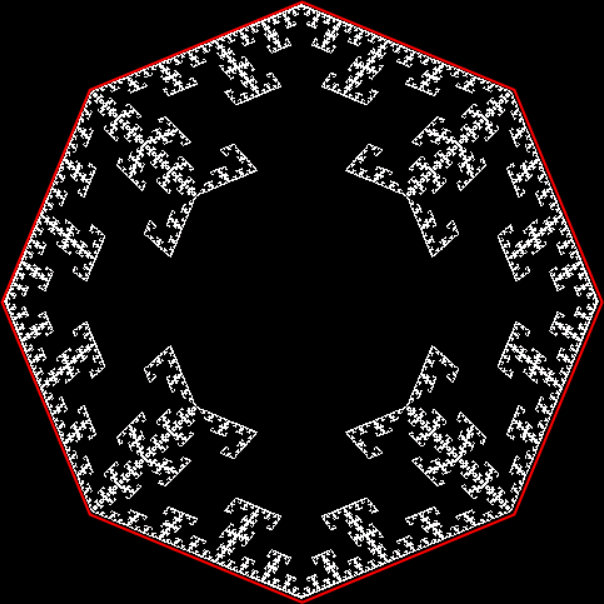
Octagon from T-square fractal

As with the Sierpiński trisc, you can use the T-squisc to create the T-octagon:

T-square fractal → T-squisc → T-octagon (color)

Or you can convert the T-square directly into the T-octagon:

T-square fractal to T-octagon fractal

But using the squisc makes for interesting multiple images:

T-square fractal → T-squisc → T-octagon (b&w)

T-square fractal → T-squisc → T-octagon → T-squisc

T-square fractal → T-squisc → T-octagon → T-squisc (animated at Ezgif)

The conversions from polygon to polygon look best when the number of sides in the higher polygon are a multiple of the number of sides in the lower, like this:

Sierpiński triangle → Sierpiński hexagon → Sierpiński nonagon

Points Pared

by in Geometry, Hexagons, Mathematics, Squares, Triangles and tagged , , , , , , | Leave a comment

There are an infinite number of points in the plane. And in part of the plane. So you have to pare points to create interesting shapes. And one way of paring them is by comparing them. The six red dots in the image below mark the three vertices of an equilateral triangle and the three mid-points of the sides. Now, test the other points in the surrounding plane and mark them in white if the average distance to (the centers of) any two of the red dots is equal to the average distance to (the centers of) the four other red dots:

Triangle + 1 side-point, sum(d1,d2)/2 = sum(d3,d4,d5,d6)/4

(click for larger)

Add a central red dot to the triangle and you get this pattern:

Triangle + 1 side-point + center, distfunc(2) = distfunc(5)

And so on:

v = 3 + sd = 2, distfunc(2) = distfunc(7)

v = 3 + sd = 2 + center, distfunc(2) = distfunc(7)

v = 3 + sd = 1, distfunc(3) = distfunc(3)

v = 3 + sd = 1 + center, distfunc(3) = distfunc(7)

v = 4 + center, distfunc(2) = distfunc(3)

v = 4 + sd = 1, distfunc(2) = distfunc(6)

v = 4 + sd = 1 + center, distfunc(2) = distfunc(7)

v = 4 + sd = 2, distfunc(2) = distfunc(10)

v = 4 + sd = 2, distfunc(2) = distfunc(10) (enlarged)

v = 4 + sd = 1, distfunc(3) = distfunc(5)

v = 4 + sd = 1, distfunc(4) = distfunc(4)

v = 5 + sd = 1, distfunc(2) = distfunc(8)

v = 5 + sd = 1, distfunc(2) = distfunc(8) (smaller scale)

v = 6 + sd = 1, distfunc(1) = distfunc(11)

v = 6 + sd = 1 + center, distfunc(1) = distfunc(12)

v = 6, distfunc(2) = distfunc(4)

v = 6 + center, distfunc(2) = distfunc(5)

v = 6, distfunc(3) = distfunc(3)

v = 6 + center, distfunc(3) = distfunc(4)

Mods and Clockers

by in Fractals, Geometry, Integer Sequences, Mathematics, Triangles and tagged , , , , , | Leave a comment

To understand clock-arithmetic, simply picture a clock-face with one hand and a big fat 0 in place of the 12. Now you can do some clock-arithmetic. For example, set the hour-hand to 5, then move on 4 hours. You’ve done this sum:

5 + 4 → 9

Now try 9 + 7. The hour-hand is already on 9, so move forward 7 hours:

9 + 7 → 4

Now try 3 + 8 + 1:

3 + 8 + 1 → 0

And 3 * 4:

4 * 3 = 4 + 4 + 4 → 0

That’s clock-arithmetic. But you’re not confined to 12-hour clocks. Here’s a 7-hour clock, where the 7 is replaced with a 0:

3 + 1 → 4
4 + 5 → 2
2 + 4 + 1 → 0
3 * 3 = 3 + 3 + 3 → 2

Another name for clock-arithmetic is modular arithmetic, because the clocks model the process of dividing a number by 12 or 7 and finding the remainder or residue — 12 or 7 is known as the modulus (and modulo is Latin for “by the modulus”).

5 + 4 = 9 → 9 / 12 = 0*12 + 9

(5 + 4) modulo 12 = 9

3 + 8 + 1 = 12 → 12 / 12 = 1*12 + 0

(3 + 8 + 1) modulo 12 = 0

19 / 12 = 1*12 + 7

19 mod 12 = 7

3 + 1 = 4 → 4 / 7 = 0*7 + 4

(3 + 1) mod 7 = 4

2 + 4 + 1 = 7 → 7 / 7 = 1*7 + 0

(2 + 4 + 1) mod 7 = 0

19 / 7 = 2*7 + 5

19 mod 7 = 5

Modular arithmetic can do wonderful things. One small but beautiful example is the way it can uncover hidden fractals in Pascal’s triangle:

Pascal’s Triangle (via Desmos)

How to create Pascal’s triangle (via Wikipedia)

If you color all numbers n mod 2 = 1 (i.e., odd numbers) in the triangle, they create the famous Sierpiński triangle:

The Sierpiński triangle in Pascal’s triangle (via Fractal Foundation)

↓

Pascal’s triangle, n mod 2 = 1 (click for larger)

The Sierpiński triangle appears like this for all n mod 4 = 2 in Pascal’s triangle:

Pascal’s triangle, n mod 4 = 2 (click for larger)

And so on:

Pascal’s triangle, n mod 8 = 4

Pascal’s triangle, n mod 16 = 8

Pascal’s triangle, n mod 32 = 16

Pascal’s triangle, n mod 64 = 32

Pascal’s triangle, n mod 128 = 64

Pascal’s triangle, n mod 256 = 128

Pascal’s triangle, n mod 2,4,8… = 1,2,4… (animated via EzGif)

Post-Performative Post-Scriptum

There’s no need to calculate Pascal’s triangle in full to find the fractals above. The 10th row of Pascal’s triangle is this:

1, 10, 45, 120, 210, 252, 210, 120, 45, 10, 1

The 20th row is this:

1, 20, 190, 1140, 4845, 15504, 38760, 77520, 125970, 167960, 184756, 167960, 125970, 77520, 38760, 15504, 4845, 1140, 190, 20, 1

And the 29th is this:

1, 29, 406, 3654, 23751, 118755, 475020, 1560780, 4292145, 10015005, 20030010, 34597290, 51895935, 67863915, 77558760, 77558760, 67863915, 51895935, 34597290, 20030010, 10015005, 4292145, 1560780, 475020, 118755, 23751, 3654, 406, 29, 1

But you don’t need to consider those ever-growing numbers in the triangle when you’re finding fractals with modular arithmetic. When the modulus is 2, you just work with 0 and 1, that is, you add the previous numbers in the triangle and find the sum modulo 2. When the modulus is 4, you just work with 0, 1, 2 and 3, adding the numbers and finding the sum modulo 4. When it’s 8, you just work with 0, 1, 2, 3, 4, 5, 6 and 7, finding the sum modulo 8. And so on.

Trigging Triangles

by in Fractals, Geometry, Mathematics, Triangles and tagged , , , , , , , , , , | Leave a comment

A fractal is a shape in which a part looks like the whole. Trees are fractals. And lungs. And clouds. But there are man-made fractals too and probably the most famous of them all is the Sierpiński triangle, invented by the Polish mathematician Wacław Sierpiński (1882-1969):

Sierpiński triangle

There are many ways to create a Sierpiński triangle, but one of the simplest is to trace all possible routes followed by a point jumping halfway towards the vertices of an equilateral triangle. If you mark the endpoint of the jumps, the Sierpiński triangle appears as the routes get longer and longer, like this:

Point jumping 1/2 way towards vertices of an equilateral triangle (animated)

Once you’ve created a Sierpiński triangle like that, you can play with it. For example, you can use simple trigonometry to stretch the triangle into a circle:

Sierpiński triangle to circle stage #1

Sierpiński triangle to circle #2

Sierpiński triangle to circle #3

Sierpiński triangle to circle #4

Sierpiński triangle to circle #5

Sierpiński triangle to circle #6

Sierpiński triangle to circle #7

Sierpiński triangle to circle #8

Sierpiński triangle to circle #9

Sierpiński triangle to circle #10

Sierpiński triangle to Sierpiński circle (animated)

But the trigging of the triangle can go further. You can expand the Sierpiński circle further, like this:

Sierpiński circle expanded

Or shrink the Sierpiński triangle like this:

Shrinking Sierpiński triangle stage #1

Shrinking Sierpiński triangle #2

Shrinking Sierpiński triangle #3

Shrinking Sierpiński triangle #4

Shrinking Sierpiński triangle #5

Shrinking Sierpiński triangle #6

Shrinking Sierpiński triangle (animated)

You can also create new shapes using the jumping-point technique. Suppose that, as the point is jumping, you adjust its position outwards into the circumscribed circle whenever it lands within the boundaries of the governing triangle. But if the point lands outside those boundaries, you leave it alone. Using this adapted technique, you get a shape like this:

Adjusted Sierpiński circle

And if the point is swung by 60° after it’s adjusted into the circle, you get a shape like this:

Adjusted Sierpiński circle (60° swing)

Here are some animated gifs showing these shapes rotating in a full circle at various speeds:

Adjusted Sierpiński circle (swinging animation) (fast)

Adjusted Sierpiński circle (swinging animation) (medium)

Adjusted Sierpiński circle (swinging animation) (slow)

Arty Fish Haul

by in Fractals, Mathematics, Triangles and tagged , , , , , , , , | Leave a comment

When is a fish a reptile? When it looks like this:

Fish from four isosceles right triangles

The fish-shape can be divided into eight identical sub-copies of itself. That is, it can be repeatedly tiled with copies of itself, so it’s an example of what geometry calls a rep-tile:

Fish divided into eight identical sub-copies

Fish divided again

Fish divided #4

Fish divided #5

Fish divided #6

Fish (animated rep-tiling)

Now suppose you divide the fish, then discard one of the sub-copies. And carry on dividing-and-discarding like that:

Fish discarding sub-copy 7 (#1)

Fish discarding sub-copy 7 (#2)

Fish discarding sub-copy 7 (#3)

Fish discarding sub-copy 7 (#4)

Fish discarding sub-copy 7 (#5)

Fish discarding sub-copy 7 (#6)

Fish discarding sub-copy 7 (#7)

Fish discarding sub-copy 7 (animated)

Here are more examples of the fish sub-dividing, then discarding sub-copies:

Fish discarding sub-copy #1

Fish discarding sub-copy #2

Fish discarding sub-copy #3

Fish discarding sub-copy #4

Fish discarding sub-copy #5

Fish discarding sub-copy #6

Fish discarding sub-copy #7

Fish discarding sub-copy #8

Fish discarding sub-copies (animated)

Now try a square divided into four copies of the fish, then sub-divided again and again:

Fish-square #1

Fish-square #2

Fish-square #3

Fish-square #4

Fish-square #5

Fish-square #6

Fish-square (animated)

The fish-square can be used to create more symmetrical patterns when the divide-and-discard rule is applied. Here’s the pattern created by dividing-and-discarded two of the sub-copies:

Fish-square divide-and-discard #1

Fish-square divide-and-discard #2

Fish-square divide-and-discard #3

Fish-square divide-and-discard #4

Fish-square divide-and-discard #5

Fish-square divide-and-discard #6

Fish-square divide-and-discard #7

Fish-square divide-and-discard #8 (delayed discard)

Fish-square divide-and-discard (animated)

Using simple trigonometry, you can convert the square pattern into a circular pattern:

↓

Circular version

Square to circle (animated)

Here are more examples of divide-and-discard fish-squares:

Fish-square divide-and-discard #1

Fish-square divide-and-discard #2

Fish-square divide-and-discard #3

Fish-square divide-and-discard #4

Fish-square divide-and-discard #5

Fish-square divide-and-discard #6

And more examples of fish-squares being converted into circles:

Fish-square to circle #1 (animated)

Fish-square to circle #2

Fish-square to circle #3

Fish-square to circle #4

Fish-square to circle #5

Fish-square to circle #6

Square Routes Re-Re-Re-Re-Re-Re-Revisited

by in Fractals, Geometry, Mathematics, Pentagons, Polygons, Squares, Triangles and tagged , , , , , , , , | Leave a comment

Suppose you trace all possible routes followed by a point inside a triangle jumping halfway towards one or another of the three vertices of the triangle. If you mark each jump, you get a famous geometrical shape called the Sierpiński triangle (or Sierpiński sieve).

Sierpiński triangle found by tracing all possible routes for a point jumping halfway towards the vertices of a triangle

The Sierpiński triangle is a fractal, because it contains copies of itself at smaller and smaller scales. Now try the same thing with a square. If you trace all possible routes followed by a point inside a square jumping halfway towards one or another of the four vertices of the square, you don’t get an obvious fractal. Instead, the interior of the square fills steadily (and will eventually be completely solid):

Routes of a point jumping halfway towards vertices of a square

Try a variant. If the point is banned from jumping towards the same vertex twice or more in a row, the routes trace out a fractal that looks like this:

Ban on choosing same vertex twice or more in a row

If the point is banned from jumping towards the vertex one place anti-clockwise of the vertex it’s just jumped towards, you get a fractal like this:

Ban on jumping towards vertex one place anti-clockwise of previously chosen vertex

And if the point can’t jump towards two places clockwise or anti-clockwise of the currently chosen vertex, this fractal appears (called a T-square fractal):

Ban on jumping towards the vertex diagonally opposite of the previously chosen vertex

That ban is equivalent to banning the point from jumping from the vertex diagonally opposite to the vertex it’s just jumped towards. Finally, here’s the fractal created when you ban the point from jumping towards the vertex one place clockwise of the vertex it’s just jumped towards:

Ban on jumping towards vertex one place clockwise of previously chosen vertex

As you can see, the fractal is a mirror-image of the one-place-anti-clockwise-ban fractal.

I discovered the ban-construction of those fractals more than twenty years ago. Then I found that I was re-discovering the same fractals when I looked at what first seemed like completely different ways of constructing fractals. There are lots of different routes to the same result. I’ve recently discovered yet another route. Let’s try what seems like an entirely different way of constructing fractals. Take a square and erect four new half-sized squares, sq1, sq2, sq3, sq4, on each corner. Then erect three more quarter-sized squares on the outward facing corners of sq1, sq2, sq3 and sq4. Carry on doing that and see what happens at the end when you remove all the previous stages of construction:

Animation of the new construction

Animation in black-and-white

It’s the T-square fractal again. Now try rotating the squares you add at stage 3 and see what happens (the rotation means that two new squares are added on adjacent outward-facing corners and one new square on the inward-facing corner):

Animation of the construction

It’s the one-place-clockwise-ban fractal again. Now try rotating the squares two places, so that two new squares are added on diagonally opposite outward-facing corners and one new square on the inward-facing corner:

Animation of the construction

It’s the same-vertex-ban fractal again. Finally, rotate squares one place more:

Animation of the construction

It’s the one-place-clockwise-ban fractal again. And this method isn’t confined to squares. Here’s what happens when you add 5/8th-sized triangles to the corners of triangles:

Animation of the construction

And here’s what happens when you add 5/13th-sized pentagons to the corners of pentagons:

Animation of the construction

Finally, here’s a variant on that pentagonal fractal (adding two rather than four pentagons at stage 3 and higher):

Animation of the construction

Previously pre-posted (please peruse):

• Square Routes
• Square Routes Revisited
• Square Routes Re-Revisited
• Square Routes Re-Re-Revisited
• Square Routes Re-Re-Re-Revisited
• Square Routes Re-Re-Re-Re-Revisited
• Square Routes Re-Re-Re-Re-Re-Revisited

The Hex Fractor #3

by in Fractals, Geometry, Mathematics, Triangles and tagged , , , , , , , , | Leave a comment

In “Diamonds to Dust”, I showed how the Mitsubishi logo could be turned into a fractal, like this:

The Mitsubishi diamonds (source)

↓

↓

Mitsubishi logo to fractal (animated)

Now I want to look at another famous symbol and its fractalization. Here’s the symbol, the hexagram:

Hexagram, a six-pointed star

The hexagram can be dissected into twelve equilateral triangles like this:

Hexagram dissected into 12 equilateral triangles

If each triangle in the dissection is replaced by a hexagram, then the hexagram is dissected again into twelve triangles, you get a famous fractal, the Koch snowflake:

The Koch snowflake

The Koch snowflake again

Hexagram to Koch snowflake (animated)

If you color the triangles, you get something like this:

Colored hexagram to fractal (animated)

Of course, this is a very inefficient way to create a Koch snowflake, because the interior hexagrams consume processing time while not contributing to the fractal boundary of the snowflake. But in a way you can fully fractalize the hexagram if you draw only the point at the center of each triangle and then color it according to how many times the pixel in question has been drawn on before. To see how this works, first look at what happens when the center-points are represented in white:

White center-points (animated)

And here’s the fully fractalized hexagram, with colored center-points:

Colored center-points (animated)

Previously Pre-Posted…

• The Hex Fractor #1 — hexagons and fractals
• The Hex Fractor #2 — hexagons and fractals again
• Diamonds to Dust — turning the Mitsubishi logo into a fractal

Trim Pickings

by in Fractals, Geometry, Mathematics, Rep-Tiles, Triangles and tagged , , , , , , | Leave a comment

Here is an equilateral triangle divided into nine smaller equilateral triangles:

Rep-9 equilateral triangle

The triangle is a rep-tile — it’s tiled with repeating copies of itself. In this case, it’s a rep-9 triangle. Each of the nine smaller triangles can obviously be divided in their turn:

Rep-81 equilateral triangle

Rep-729 equilateral triangle

Rep-729 equilateral triangle again

Rep-6561 equilateral triangle

Rep-9 triangle repeatedly subdividing (animated)

How try trimming the original rep-9 triangle, picking one of the trimmings, and repeating in finer detail. If you choose six triangles in this pattern, you can create a symmetrical braided fractal:

Triangular fractal stage 1

Triangular fractal #2

Triangular fractal #3

Triangular fractal #3 (cleaning up)

Triangular fractal #3 (cleaning up more)

Triangular fractal #4

Triangular fractal #5

Triangular fractal #6

Triangular fractal (animated)

But this fractal using a three-triangle trim-picking isn’t symmetrical:

Trim-picking #1

Trim-picking #2

Trim-picking #3

Trim-picking #4

Trim-picking #5

To make it symmetric, you have to delay the trim, using the full rep-9 trim for the first stage:

Delayed trim-picking #1

Delayed trim-picking #2

Delayed trim-picking #3

Delayed trim-picking #4

Delayed trim-picking #5

Delayed trim-picking #6 (with first two stages as rep-9)

Delayed trim-picking (animated)

Here are some more delayed trim-pickings used to created symmetrical patterns:

Polykoch (Kontinued)

by in Fractals, Geometry, Mathematics, Polygons, Squares, Triangles and tagged , , , , , , , , , , | Leave a comment

In “Polykoch!”, I looked at variants on the famous Koch snowflake, which is created by erecting new triangles on the sides of an equilaternal triangle, like this:

Koch snowflake #1

Koch snowflake #2

Koch snowflake #3

Koch snowflake #4

Koch snowflake #5

Koch snowflake #6

Koch snowflake #7

Koch snowflake (animated)

One variant is simple: the new triangles move inward rather than outward:

Inverted Koch snowflake #1

Inverted Koch snowflake #2

Inverted Koch snowflake #3

Inverted Koch snowflake #4

Inverted Koch snowflake #5

Inverted Koch snowflake #6

Inverted Koch snowflake #7

Inverted Koch snowflake (animated)

Or you can alternate between moving the new triangles inward and outward. When they always move outward and have sides 1/5 the length of the sides of the original triangle, the snowflake looks like this:

When they move inward, then always outward, the snowflake looks like this:

And so on:

Now here’s a Koch square with its new squares moving inward:

Inverted Koch square #1

Inverted Koch square #2

Inverted Koch square #3

Inverted Koch square #4

Inverted Koch square #5

Inverted Koch square #6

Inverted Koch square (animated)

And here’s a pentagon with squares moving inwards on its sides:

Pentagon with squares #1

Pentagon with squares #2

Pentagon with squares #3

Pentagon with squares #4

Pentagon with squares #5

Pentagon with squares #6

Pentagon with squares (animated)

And finally, an octagon with hexagons on its sides. First the hexagons move outward, then inward, then outward, then inward, then outward:

Octagon with hexagons #1

Octagon with hexagons #2

Octagon with hexagons #3

Octagon with hexagons #4

Octagon with hexagons #5

Octagon with hexagons (animated)

Polykoch!

by in Fractals, Geometry, φ, Mathematics, Pentagons, Phi, Squares, Triangles and tagged , , , , , , , , , | Leave a comment

This is how you form the famous Koch snowflake, in which at each stage you erect a new triangle on the middle of each line whose sides are 1/3 the length of the line:

Koch snowflake #1

Koch snowflake #2

Koch snowflake #3

Koch snowflake #4

Koch snowflake #5

Koch snowflake #6

Koch snowflake #7

Koch snowflake (animated)

Here’s a variant of the Koch snowflake, with new mid-triangles whose sides are 1/2 the length of the lines:

Koch snowflake (1/2 side) #1

Koch snowflake (1/2 side) #2

Stage #3

Stage #4

Stage #5

Stage #6

Stage #7

Stage #8

Koch snowflake (1/2 side) (animated)

But why stop at triangles? This is a Koch square, in which at each stage you erect a new 1/3 square on the middle of each line:

Koch square #1

Koch square #2

Koch square #3

Koch square #4

Koch square #5

Koch square #6

Koch square (animated)

And a Koch pentagon, in which at each stage you erect a pentagon on the middle of each line whose sides are 1 – (1/φ^2 * 2) = 0·236067977… the length of the line (I used 55/144 as an approximation of 1/φ^2):

Koch pentagon (side 55/144) #1

Koch pentagon #2

Koch pentagon #3

Koch pentagon #4

Koch pentagon #5

Koch pentagon #6

Koch pentagon (animated)

In this close-up, you can see how precisely the sprouting pentagons kiss at each stage:

Koch pentagon (close-up) #1

Koch pentagon (close-up) #2

Koch pentagon (close-up) #3

Koch pentagon (close-up) #4

Koch pentagon (close-up) #5

Koch pentagon (close-up) #6

Koch pentagon (close-up) (animated)