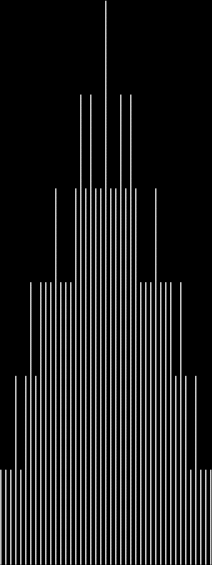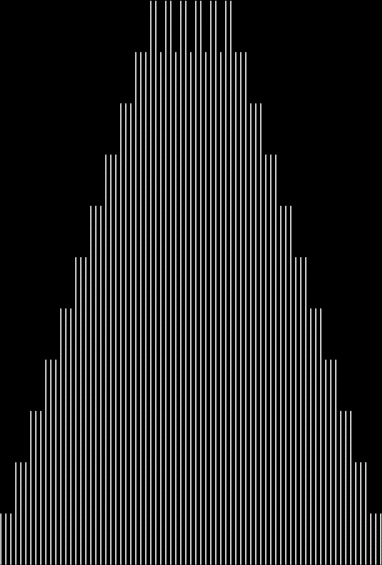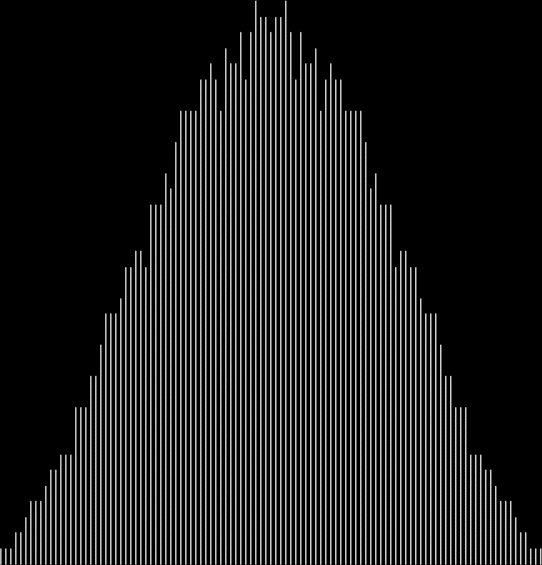Absolutely Sabulous

by in A.E. Housman, Literature, Poetry, The Sea and tagged , , , , , , , , , , | Leave a comment

Smooth between sea and land
Is laid the yellow sand,
And here through summer days
The seed of Adam plays.

Here the child comes to found
His unremaining mound,
And the grown lad to score
Two names upon the shore.

Here, on the level sand,
Between the sea and land,
What shall I build or write
Against the fall of night?

Tell me of runes to grave
That hold the bursting wave,
Or bastions to design
For longer date than mine.

Shall it be Troy or Rome
I fence against the foam,
Or my own name, to stay
When I depart for aye?

Nothing: too near at hand,
Planing the figure sand,
Effacing clean and fast
Cities not built to last
And charms devised in vain,
Pours the confounding main. — A.E. Housman, “XLV” of More Poems (1936)

Summer-Time Hues

by in Arithmetic, Mathematics | Leave a comment

sum(4,17) = 147 = 4 + 5 + 6 + 7 + 8 + 9 + 10 + 11 + 12 + 13 + 14 + 15 + 16 + 17
sum(1,20) = 210
sum(19,59) = 1599
sum(22,77) = 2772
sum(20,156) = 12056
sum(34,167) = 13467
sum(23,211) = 22113
sum(79,227) = 22797
sum(84,229) = 22849
sum(61,236) = 26136
sum(199,599) = 159999
sum(203,771) = 277103
sum(222,777) = 277722
sum(266,778) = 267786
sum(277,797) = 279777
sum(145,1520) = 1145520
sum(117,1522) = 1152217
sum(149,1525) = 1152549
sum(167,1527) = 1152767
sum(208,1568) = 1208568
sum(334,1667) = 1334667
sum(540,1836) = 1540836
sum(315,1990) = 1931590
sum(414,2062) = 2041462
sum(418,2063) = 2041863
sum(158,2083) = 2158083
sum(244,2132) = 2244132
sum(554,2139) = 2135549
sum(902,2347) = 2349027
sum(883,2558) = 2883558
sum(989,2637) = 2989637
sum(436,2963) = 4296336
sum(503,3303) = 5330303
sum(626,3586) = 6235866
sum(816,4183) = 8418316
sum(1075,4700) = 10470075
sum(1117,4922) = 11492217
sum(1306,5273) = 13052736
sum(1377,5382) = 13538277
sum(1420,5579) = 14557920
sum(1999,5999) = 15999999
sum(2727,7272) = 22727727
sum(2516,7528) = 25175286
sum(2625,7774) = 26777425
sum(2222,7777) = 27777222
sum(3765,9490) = 37949065
sum(535,10319) = 53103195
sum(1101,14973) = 111497301
sum(2088,15688) = 120885688
sum(3334,16667) = 133346667
sum(2603,19798) = 192603798
sum(3093,19893) = 193093893
sum(1162,20039) = 200116239
sum(1415,20095) = 200914155
sum(1563,20118) = 201156318
sum(2707,20294) = 202270794
sum(2518,20318) = 203251818
sum(2608,20333) = 203326083
sum(2895,20370) = 203289570
sum(3424,20552) = 205342452
sum(4255,20855) = 208425555
sum(4571,20971) = 209457171
sum(4613,21028) = 210461328
sum(4742,21259) = 214742259
sum(6318,21798) = 217631898
sum(6498,21943) = 219649843
sum(7080,22305) = 223708005
sum(7243,22358) = 223724358
sum(6833,22368) = 226833368
sum(7128,22473) = 227128473
sum(4523,22603) = 245232603
sum(4978,22898) = 249782898
sum(8339,23019) = 230183399
sum(8610,23191) = 231861091
sum(6013,23588) = 260133588
sum(9252,23652) = 236925252
sum(6488,23913) = 264883913
sum(8379,25254) = 283795254
sum(4012,28667) = 402866712
sum(4922,31762) = 492317622
sum(4998,31801) = 493180198
sum(5200,32675) = 520326750
sum(7707,40092) = 774009207
sum(7868,40431) = 786404318
sum(9325,44450) = 944450325
sum(11047,48287) = 1104828747
sum(14699,56100) = 1465610099
sum(16235,59860) = 1659860235
sum(19999,59999) = 1599999999
sum(17264,61239) = 1726123964
sum(17405,61605) = 1746160505
sum(18457,63782) = 1863782457
sum(25016,75028) = 2501750286
sum(28022,79942) = 2802799422
sum(37060,93740) = 3706937400
sum(7567,119567) = 7119567567
sum(9638,135513) = 9135513638
sum(15392,152607) = 11526075392
sum(17744,152880) = 11528807744
sum(12012,156387) = 12156387012
sum(20888,156888) = 12088856888
sum(30663,164538) = 13066364538
sum(33334,166667) = 13333466667
sum(36038,168838) = 13603868838

Aventurhyme

by in A.E. Housman, Literature, Poetry and tagged , , , , , , , , | Leave a comment

The Merry Guide

Once in the wind of morning
     I ranged the thymy wold;
The world-wide air was azure
     And all the brooks ran gold.

There through the dews beside me
     Behold a youth that trod,
With feathered cap on forehead,
     And poised a golden rod.

With mien to match the morning
     And gay delightful guise
And friendly brows and laughter
     He looked me in the eyes.

Oh whence, I asked, and whither?
     He smiled and would not say,
And looked at me and beckoned
      And laughed and led the way.

And with kind looks and laughter
     And nought to say beside
We two went on together,
     I and my happy guide.

Across the glittering pastures
     And empty upland still
And solitude of shepherds
     High in the folded hill,

By hanging woods and hamlets
     That gaze through orchards down
On many a windmill turning
     And far-discovered town,

With gay regards of promise
     And sure unslackened stride
And smiles and nothing spoken
     Led on my merry guide.

By blowing realms of woodland
     With sunstruck vanes afield
And cloud-led shadows sailing
     About the windy weald,

By valley-guarded granges
     And silver waters wide,
Content at heart I followed
     With my delightful guide.

And like the cloudy shadows
     Across the country blown
We two fare on for ever,
     But not we two alone.

With the great gale we journey
     That breathes from gardens thinned,
Borne in the drift of blossoms
      Whose petals throng the wind;

Buoyed on the heaven-heard whisper
     Of dancing leaflets whirled
From all the woods that autumn
     Bereaves in all the world.

And midst the fluttering legion
     Of all that ever died
I follow, and before us
     Goes the delightful guide,

With lips that brim with laughter
     But never once respond,
And feet that fly on feathers,
     And serpent-circled wand.

• A.E. Housman, A Shropshire Lad, XLII

An aventurine obelisk (Unlimited Crystals)

Factory Façades

by in Arithmetic, Mathematics and tagged , , , , , , | Leave a comment

Practically speaking, I’d never heard of them. Practical numbers, that is. They’re defined like this at the Online Encyclopedia of Integer Sequences:

A005153 Practical numbers: positive integers m such that every k <= sigma(m) is a sum of distinct divisors of m. Also called panarithmic numbers. […] Equivalently, positive integers m such that every number k <= m is a sum of distinct divisors of m. — A005153 at OEIS

In other words, if you take, say, divisors(12) = 1, 2, 3, 4, 6, you can find partial sums of those divisors that equal every number from 1 to 16, where 16 = 1+2+3+4+6. Here are all those sums, with c as the count of divisor-sums equalling a particular k (to simplify things, I’m excluding 12 as a divisor of 12):

1, 2, 3, 4, 6 = divisors(12)

01 = 1 (c=1)
02 = 2 (c=1)
03 = 1 + 2 = 3 (c=2)
04 = 1 + 3 = 4 (c=2)
05 = 2 + 3 = 1 + 4 (c=2)
06 = 1 + 2 + 3 = 2 + 4 = 6 (c=3)
07 = 1 + 2 + 4 = 3 + 4 = 1 + 6 (c=3)
08 = 1 + 3 + 4 = 2 + 6 (c=2)
09 = 2 + 3 + 4 = 1 + 2 + 6 = 3 + 6 (c=3)
10 = 1 + 2 + 3 + 4 = 1 + 3 + 6 = 4 + 6 (c=3)
11 = 2 + 3 + 6 = 1 + 4 + 6 (c=2)
12 = 1 + 2 + 3 + 6 = 2 + 4 + 6 (c=2)
13 = 1 + 2 + 4 + 6 = 3 + 4 + 6 (c=2)
14 = 1 + 3 + 4 + 6 (c=1)
15 = 2 + 3 + 4 + 6 (c=1)
16 = 1 + 2 + 3 + 4 + 6 (c=1)

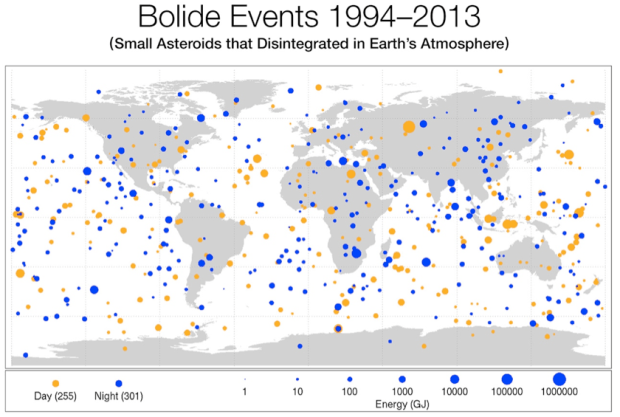
Learning about practical numbers inspired me to look at the graphs of the count of the divisor-sums for 12. If you include count(0) = 1 (there is one way of choosing divisors of 12 to equal 0, namely, by choosing none of the divisors), the graph looks like this:

counts of divisorsum(12) = k, where 12 = 2^2 * 3 → 1, 2, 3, 4, 6

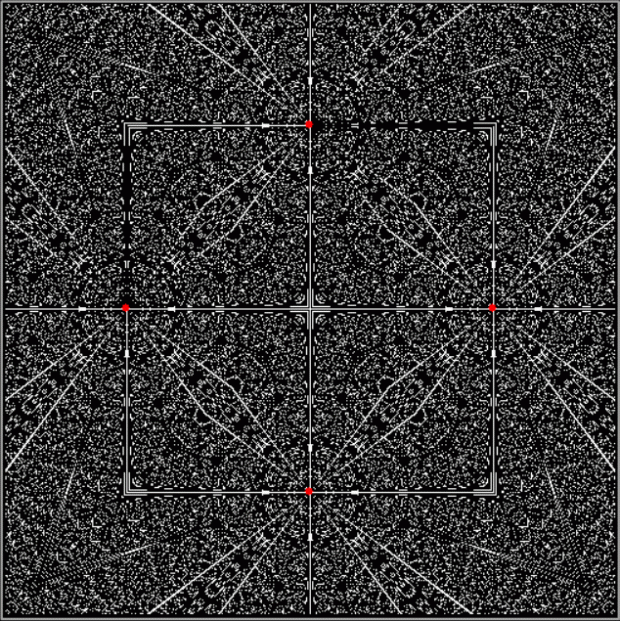
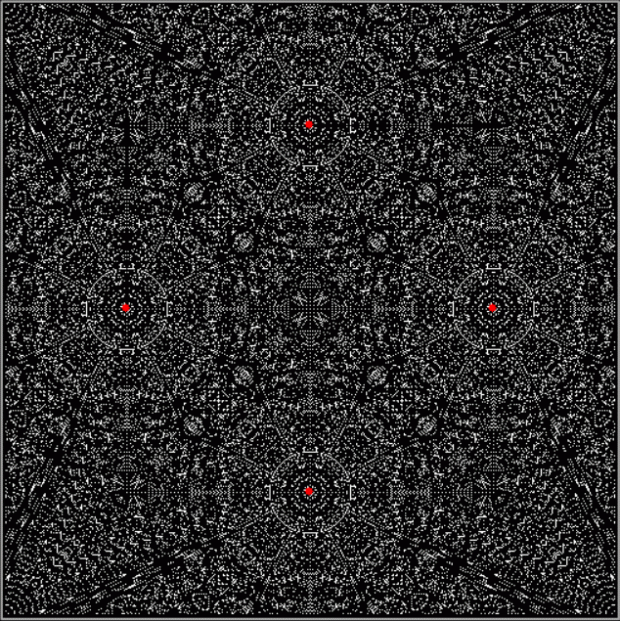
Here are some more graphs for partialsumcount(n), adjusted for a standardized y-max. They remind me variously of skyscrapers, pyramids, stupas, factories and factory façades, forts bristling with radar antennae, and the Houses of Parliament. All in an art-deco style:

18 = 2 * 3^2 → 1, 2, 3, 6, 9

24 = 2^3 * 3 → 1, 2, 3, 4, 6, 8, 12

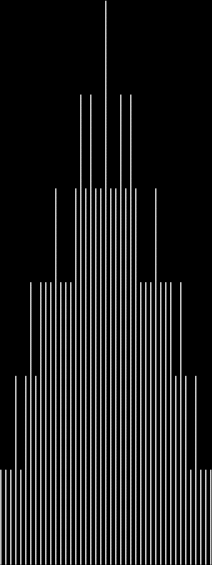
30 = 2 * 3 * 5 → 1, 2, 3, 5, 6, 10, 15

36 = 2^2 * 3^2 → 1, 2, 3, 4, 6, 9, 12, 18

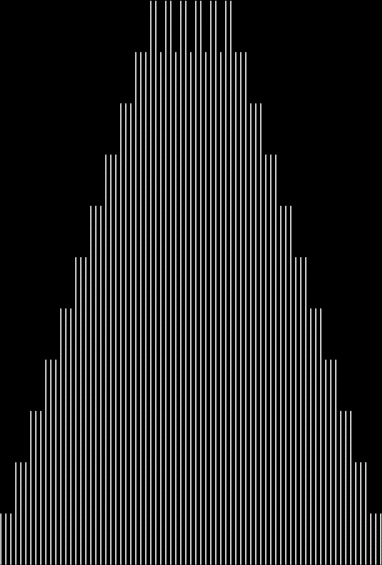
48 = 2^4 * 3 → 1, 2, 3, 4, 6, 8, 12, 16, 24

54 = 2 * 3^3 → 1, 2, 3, 6, 9, 18, 27

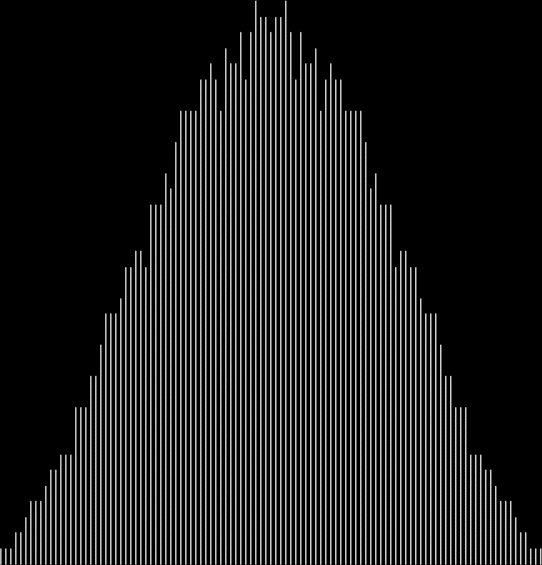
60 = 2^2 * 3 * 5 → 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30

72 = 2^3 * 3^2 → 1, 2, 3, 4, 6, 8, 9, 12, 18, 24, 36

88 = 2^3 * 11 → 1, 2, 4, 8, 11, 22, 44, 88

96 = 2^5 * 3 → 1, 2, 3, 4, 6, 8, 12, 16, 24, 32, 48

100 = 2^2 * 5^2 → 1, 2, 4, 5, 10, 20, 25, 50

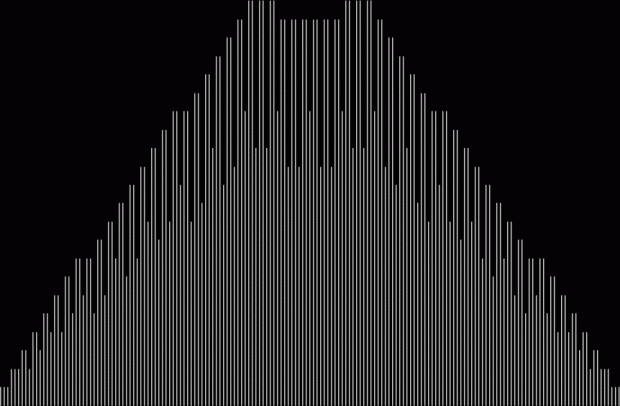
108 = 2^2 * 3^3 → 1, 2, 3, 4, 6, 9, 12, 18, 27, 36, 54

120 = 2^3 * 3 * 5 → 1, 2, 3, 4, 5, 6, 8, 10, 12, 15, 20, 24, 30, 40, 60

126 = 2 * 3^2 * 7 → 1, 2, 3, 6, 7, 9, 14, 18, 21, 42, 63

162 = 2 * 3^4 → 1, 2, 3, 6, 9, 18, 27, 54, 81

220 = 2^2 * 5 * 11 → 1, 2, 4, 5, 10, 11, 20, 22, 44, 55, 110

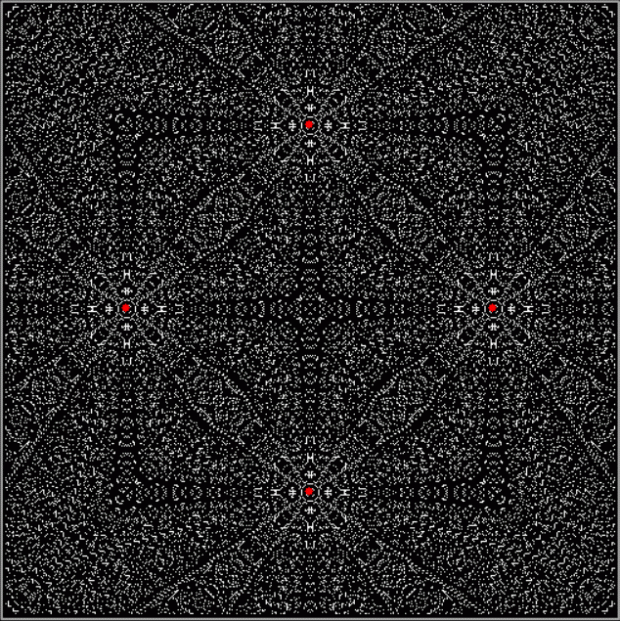
And what about im-practical numbers, where the partial sums of divisors(m) don’t equal every number 1..sigma(m)? There are interesting fractal patterns to be uncovered there, as you can see from the graph for 190 (because all divsumcount(k) = 1, the graph looks like a bar-code):

190 = 2 * 5 * 19 → 1, 2, 5, 10, 19, 38, 95

Pooh Pooh-Poohed

by in English Usage, Language and tagged , , , , , , , , | 2 Comments

A.A. Milne’s Winnie-the-Pooh (1926) is a core kiddy-culture classic. And I’ve always been a big fan. Especially of Eeyore. But it wasn’t till 2025 that I noticed a big bit of bad writing in the book. Or maybe it isn’t. Maybe the redundancy here is more natural English than the same passage with the redundancy removed. But I still think removing the redundancy makes it read better. See for yourself:

One day when he was out walking, he [Winnie-the-Pooh] came to an open place in the middle of the forest, and in the middle of this place was a large oak-tree, and, from the top of the tree, there came a loud buzzing-noise.

In this drawing, Winnie-the-Pooh is peering up. There are tiny things swarming around up there.

Winnie-the-Pooh sat down at the foot of the tree, put his head between his paws and began to think.

First of all he said to himself: “That buzzing-noise means something. You don’t get a buzzing-noise like that, just buzzing and buzzing, without its meaning something. If there’s a buzzing-noise, somebody’s making a buzzing-noise, and the only reason for making a buzzing-noise that I know of is because you’re a bee.”

Then he thought another long time, and said: “And the only reason for being a bee that I know of is making honey.”

And then he got up, and said: “And the only reason for making honey is so as I can eat it.” So he began to climb the tree. — Winnie-the-Pooh, chapter 1

↓

REMOVING

↓

REDUNDANCY

↓

One day when he was out walking, he came to an open place in the middle of the forest, and in the middle of this place was a large oak-tree, and, from the top of the tree, there came a loud buzzing.

In this drawing, Winnie-the-Pooh is peering up. There are tiny things swarming around up there.

Winnie-the-Pooh sat down at the foot of the tree, put his head between his paws and began to think.

First of all he said to himself: “That buzzing means something. You don’t get a buzzing like that, just buzzing and buzzing, without its meaning something. If there’s a buzzing, somebody’s making a buzzing, and the only reason for making a buzzing that I know of is because you’re a bee.”

Then he thought another long time, and said: “And the only reason for being a bee that I know of is making honey.”

And then he got up, and said: “And the only reason for making honey is so as I can eat it.” So he began to climb the tree. — Winnie-the-Pooh, chapter 1

Elsewhere Other-Accessible…

• Winnie-the-Pooh (1926) at Gutenberg

Previously Pre-Posted…

• Noise Annoys — discussion of the redundancy of “noise”
• Nice Noise — more discussion of the redundancy of “noise”

Weird Tails

by in Ancient Greek, French, Language, Latin, Linguistics and tagged , , , , , , , , , | Leave a comment

Squirrel

Meaning

One or other of various species of slender, graceful, agile rodents (characterized by a long bushy tail, furry coat, and bright eyes), belonging to the genus Sciurus, or to the widely-distributed sub-family Sciurina including this; esp. the common species Sciurus vulgaris, native to Britain, Europe, and parts of Asia.

Etymology

Anglo-Norman esquirel, Old French esquireul, escureul, ‑ol, etc. (modern French écureuil), = Provençal escurols, Spanish esquirol, medieval Latin (e)scurellus, scurellius, scuriolus, diminutives from popular Latin *scūrius, for Latin sciūrus, < Greek σκίουρος, apparently < σκιά shade + οὐρά tail.

• Oxford English Dictionary, entry for “Squirrel”.

Sorted for D’s nand Wizz

by in Geometry, Mathematics, Polygonal numbers, Squares, Triangular Numbers and tagged , , , , | Leave a comment

As I’ve pre-previously pointed out, there are an infinite number of points in the plane. And in part of the plane. So you have to pare points to create interesting shapes. One way of paring points is by comparing them. After you’ve compared them, you can sort them. For example, you can compare the distance from (x,y) to the four vertices of a square. Then you can sort the distances from nearest to furthest. Then you can mark (x,y) if the distance to, say, the nearest vertice from (x,y) is evenly divisible by 2 when measured in pixels or some other unit. When you do that, you might get an image like this (depending on the hardware and software you use):

Distance to nearest vertex is evenly divisible by 2, i.e. d mod 2 = 0 for v1 (vertices marked in red)

Or you can mark (x,y) if the distance to the nearest vertex is a triangular number:

is_triangular(d) for v1

Or a square number:

is_square(d) for v1

Or you can test the distance to the second-nearest vertex:

d mod 2 = 0 for v2

And the third-nearest (or second-furthest) vertex:

d mod 2 = 0 for v3

And furthest vertex:

d mod 2 = 0 for v4

Now try expanding or contracting the square:

d mod 2 = 0 for v1 on square * 2

d mod 2 = 0 for v1 on square * 3

d mod 2 = 0 for v1 on square * 0.5

d mod 2 = 0 for v1 on square * 1.5

d mod 2 = 0 for v1 on square * 5

d mod 2 = 0 for v1 on square * 20

d mod 2 = 0 for v1 on square * 100

Finally, here are some more mandala-like images created by using various d mod m on an expanded square (the images should be horizontally and vertically mirror-symmetrical, but my software introduced artefacts):

d mod 2 = 0 for v1 on square * 200
(open in separate window for better detail)

d mod 3 = 0 for v1 on square * 200

d mod 4 = 0 for v1 on square * 200

d mod 5 = 0 for v1 on square * 200

d mod 6 = 0 for v1 on square * 200

d mod 7 = 0 for p1 on square * 200

d mod 8 = 0 for p1 on square * 200

d mod 9 = 0 for p1 on square * 200

d mod 2..9 = 0 for p1 on square * 200 (animated at EZgif)

Post-Performative Post-Scriptum…

The title of this incendiary intervention is a paronomasia on “Sorted for E’s and Wizz”, a song offa of 1995 album Different Class by Sheffield Brit-popsters Pulp rebelliously referencing counter-cultural consumption of psychoactive drugs ecstasy and amphetamine. My program sorted distances, i.e. d’s, but not wizz, therefore it sorted d’s and-not wizz. In Boolean logic, nand means “and-not” (roughly speaking).

Previously Pre-Posted (Please Peruse)…

• Points Pared — an earlier look at points and polygons