Tag Archives: factors

Graph durch Euler

by in Arithmetic, Mathematics, Prime numbers and tagged , , , , , , , , , , , , , | Leave a comment

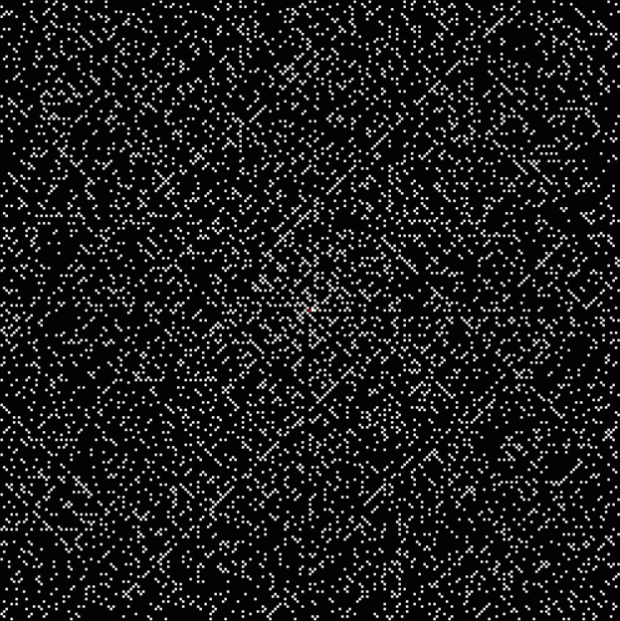
This is the famous Ulam spiral, in which prime numbers are represented on filled squares on a square spiral:

The Ulam spiral

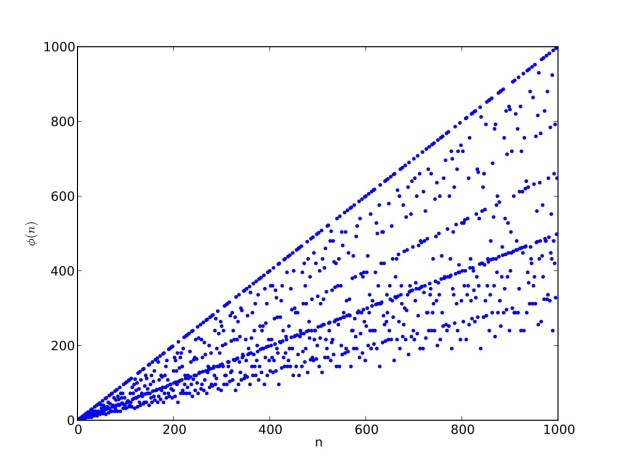
I like the way the spiral sits between chaos and calm. It’s not wholly random and it’s not wholly regular — it’s betwixt and between. You get a similar chaos-and-calm vibe from a graph for a function called Euler phi. And primes are at work there too. Here’s the graph from Wikipedia:

Graph of eulerphi(n) = φ(n) (see Euler’s totient function)

But what is the Euler phi function? For any integer n, eulerphi(n) gives you the count of numbers < n that are relatively prime to n. That is, the count of numbers < n that have no common factors with n other than one. You can see how eulerphi(n) works by considering whether you can simplify the fraction a/b, where a = 1..n-1 and b = n:

φ(6) = 2
1/6 (1)
2/6 → 1/3
3/6 → 1/2
4/6 → 2/3
5/6, ∴ φ(6) = 2

φ(7) = 6
1/7 (1)
2/7 (2)
3/7 (3)
4/7 (4)
5/7 (5)
6/7, ∴ φ(7) = 6

φ(12) = 4
1/12 (1)
2/12 → 1/6
3/12 → 1/4
4/12 → 1/3
5/12 (2)
6/12 → 1/2
7/12 (3)
8/12 → 2/3
9/12 → 3/4
10/12 → 5/6
11/12, ∴ φ(12) = 4

φ(13) = 12
1/13 (1)
2/13 (2)
3/13 (3)
4/13 (4)
5/13 (5)
6/13 (6)
7/13 (7)
8/13 (8)
9/13 (9)
10/13 (10)
11/13 (11)
12/13, ∴ φ(13) = 12

As you can see, eulerphi(n) = n-1 for primes. Now you know what the top line of the Eulerphi graph is. It’s the primes. Here’s a bigger version of the graph:

Graph of eulerphi(n) = φ(n)

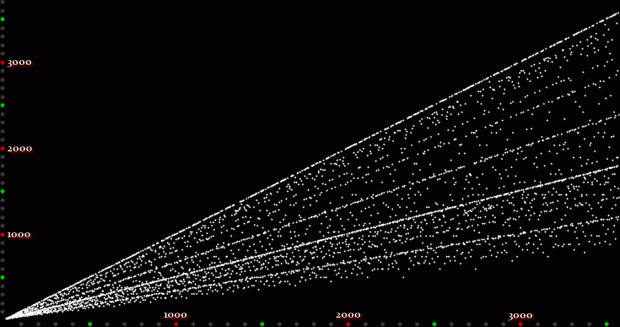
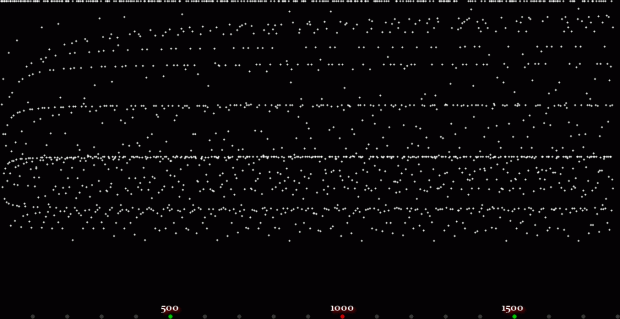
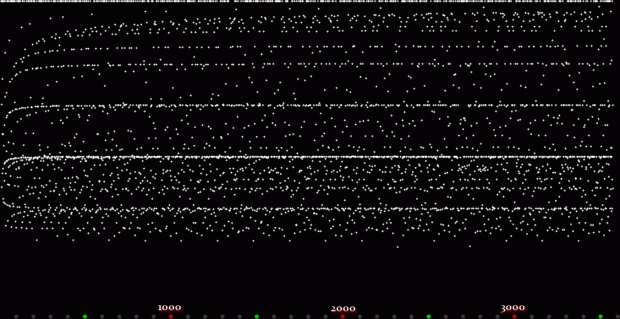
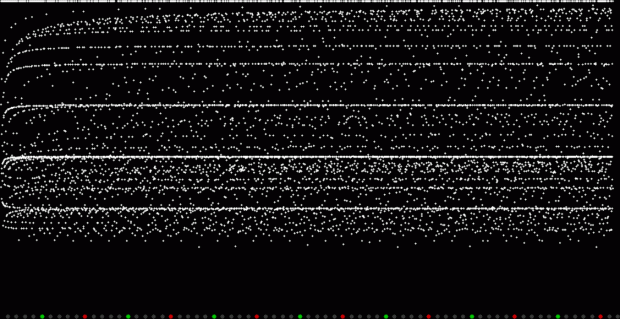
Unlike the Ulam spiral, however, the Eulerphi graph is cramped. But it’s easy to stretch it. You can represent φ(n) as a fraction between 0 and 1 like this: phifrac(n) = φ(n) / (n-1). Using phifrac(n), you can create Eulerphi bands, like this:

Eulerphi band, n <= 1781

Eulerphi band, n <= 3561

Eulerphi band, n <= 7121

Eulerphi band, n <= 14241

Or you can create Eulerphi discs, like this:

Eulerphi disc, n <= 1601

Eulerphi disc, n <= 3201

Eulerphi disc, n <= 6401

Eulerphi disc, n <= 12802

Eulerphi disc, n <= 25602

But what is the bottom line of the Eulerphi bands and inner ring of the Eulerphi discs, where φ(n) is smallest relative to n? Well, the top line or outer ring is the primes and the bottom line or inner ring is the primorials (and their multiples). The function primorial(n) is the multiple of the first n primes:

primorial(1) = 2
primorial(2) = 2*3 = 6
primorial(3) = 2*3*5 = 30
primorial(4) = 2*3*5*7 = 210
primorial(5) = 2*3*5*7*11 = 2310
primorial(6) = 2*3*5*7*11*13 = 30030
primorial(7) = 2*3*5*7*11*13*17 = 510510
primorial(8) = 2*3*5*7*11*13*17*19 = 9699690
primorial(9) = 2*3*5*7*11*13*17*19*23 = 223092870
primorial(10) = 2*3*5*7*11*13*17*19*23*29 = 6469693230

Here are the numbers returning record lows for φfrac(n) = φ(n) / (n-1):

φ(4) = 2 (2/3 = 0.666…)
4 = 2^2
φ(6) = 2 (2/5 = 0.4)
6 = 2.3
φ(12) = 4 (4/11 = 0.363636…)
12 = 2^2.3
[…]
φ(30) = 8 (8/29 = 0.275862…)
30 = 2.3.5
φ(60) = 16 (16/59 = 0.27118…)
60 = 2^2.3.5
[…]
φ(210) = 48 (48/209 = 0.229665…)
210 = 2.3.5.7
φ(420) = 96 (96/419 = 0.2291169…)
420 = 2^2.3.5.7
φ(630) = 144 (144/629 = 0.228934…)
630 = 2.3^2.5.7
[…]
φ(2310) = 480 (480/2309 = 0.2078822…)
2310 = 2.3.5.7.11
φ(4620) = 960 (960/4619 = 0.20783719…)
4620 = 2^2.3.5.7.11
[…]
30030 = 2.3.5.7.11.13
φ(60060) = 11520 (11520/60059 = 0.191811385…)
60060 = 2^2.3.5.7.11.13
φ(90090) = 17280 (17280/90089 = 0.1918103209…)
90090 = 2.3^2.5.7.11.13
[…]
φ(510510) = 92160 (92160/510509 = 0.18052571061…)
510510 = 2.3.5.7.11.13.17
φ(1021020) = 184320 (184320/1021019 = 0.18052553…)
1021020 = 2^2.3.5.7.11.13.17
φ(1531530) = 276480 (276480/1531529 = 0.180525474868579…)
1531530 = 2.3^2.5.7.11.13.17
φ(2042040) = 368640 (368640/2042039 = 0.18052544540040616…)
2042040 = 2^3.3.5.7.11.13.17

Triangular Squares

by in √2, Integer Sequences, Irrational numbers, Mathematics, Square root of 2, Square Roots, Squares, Triangular Numbers and tagged , , , , , , , , , , , , , | Leave a comment

The numbers that are both square and triangular are beautifully related to the best approximations to √2:

Number

Square Root

Factors of root
1 1 1
36 6 2 * 3
1225 35 5 * 7
41616 204 12 * 17

and so on.

In each case the factors of the root are the numerator and denominator of the next approximation to √2. — David Wells, The Penguin Dictionary of Curious and Interesting Mathematics (1986), entry for “36”.

Elsewhere other-accessible

• A001110 — Square triangular numbers: numbers that are both triangular and square

Factory Records

by in Base Behavior, Mathematics, Palindromic numbers, Prime numbers and tagged , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , | Leave a comment

The factors of n are those numbers that divide n without remainder. So the factors of 6 are 1, 2, 3 and 6. If the function s(n) is defined as “the sum of the factors of n, excluding n”, then s(6) = 1 + 2 + 3 = 6. This makes 6 a perfect number: its factors re-create it. 28 is another perfect number. The factors of 28 are 1, 2, 4, 7, 14 and 28, so s(28) = 1 + 2 + 4 + 7 + 14 = 28. Other perfect numbers are 496 and 8128. And they’re perfect in any base.

Amicable numbers are amicable in any base too. The factors of an amicable number sum to a second number whose factors sum to the first number. So s(220) = 284, s(284) = 220. That pair may have been known to Pythagoras (c.570-c.495 BC), but s(1184) = 1210, s(1210) = 1184 was discovered by an Italian schoolboy called Nicolò Paganini in 1866. There are also sociable chains, in which s(n), s(s(n)), s(s(s(n))) create a chain of numbers that leads back to n, like this:

12496 → 14288 → 15472 → 14536 → 14264 → 12496 (c=5)

Or this:

14316 → 19116 → 31704 → 47616 → 83328 → 177792 → 295488 → 629072 → 589786 → 294896 → 358336 → 418904 → 366556 → 274924 → 275444 → 243760 → 376736 → 381028 → 285778 → 152990 → 122410 → 97946 → 48976 → 45946 → 22976 → 22744 → 19916 → 17716 → 14316 (c=28)

Those sociable chains were discovered (and christened) in 1918 by the Belgian mathematician Paul Poulet (1887-1946). Other factor-sum patterns are dependant on the base they’re expressed in. For example, s(333) = 161. So both n and s(n) are palindromes in base-10. Here are more examples — the numbers in brackets are the prime factors of n and s(n):

333 (3^2, 37) → 161 (7, 23)
646 (2, 17, 19) → 434 (2, 7, 31)
656 (2^4, 41) → 646 (2, 17, 19)
979 (11, 89) → 101 (prime)
1001 (7, 11, 13) → 343 (7^3)
3553 (11, 17, 19) → 767 (13, 59)
10801 (7, 1543) → 1551 (3, 11, 47)
11111 (41, 271) → 313 (prime)
18581 (17, 1093) → 1111 (11, 101)
31713 (3, 11, 31^2) → 15951 (3, 13, 409)
34943 (83, 421) → 505 (5, 101)
48484 (2^2, 17, 23, 31) → 48284 (2^2, 12071)
57375 (3^3, 5^3, 17) → 54945 (3^3, 5, 11, 37)
95259 (3, 113, 281) → 33333 (3, 41, 271)
99099 (3^2, 7, 11^2, 13) → 94549 (7, 13, 1039)
158851 (7, 11, 2063) → 39293 (prime)
262262 (2, 7, 11, 13, 131) → 269962 (2, 7, 11, 1753)
569965 (5, 11, 43, 241) → 196691 (11, 17881)
1173711 (3, 7, 11, 5081) → 777777 (3, 7^2, 11, 13, 37)

Note how s(656) = 646 and s(646) = 434. There’s an even longer sequence in base-495:

33 → 55 → 77 → 99 → [17][17] → [19][19] → [21][21] → [43][43] → [45][45] → [111][111] → [193][193] → [195][195] → [477][477] (b=495) (c=13)
1488 (2^4, 3, 31) → 2480 (2^4, 5, 31) → 3472 (2^4, 7, 31) → 4464 (2^4, 3^2, 31) → 8432 (2^4, 17, 31) → 9424 (2^4, 19, 31) → 10416 (2^4, 3, 7, 31) → 21328 (2^4, 31, 43) → 22320 (2^4, 3^2, 5, 31) → 55056 (2^4, 3, 31, 37) → 95728 (2^4, 31, 193) → 96720 (2^4, 3, 5, 13, 31) → 236592 (2^4, 3^2, 31, 53)

I also tried looking for n whose s(n) mirrors n. But they’re hard to find in base-10. The first example is this:

498906 (2, 3^3, 9239) → 609894 (2, 3^2, 31, 1093)

498906 mirrors 609894, because the digits of each run in reverse to the digits of the other. Base-9 does better for mirror-sums, clocking up four in the same range of integers:

42 → 24 (base=9)
38 (2, 19) → 22 (2, 11)
402 → 204 (base=9)
326 (2, 163) → 166 (2, 83)
4002 → 2004 (base=9)
2918 (2, 1459) → 1462 (2, 17, 43)
5544 → 4455 (base=9)
4090 (2, 5, 409) → 3290 (2, 5, 7, 47)

Base-11 does better still, clocking up eight in the same range:

42 → 24 (base=11)
46 (2, 23) → 26 (2, 13)
2927 → 7292 (base=11)
3780 (2^2, 3^3, 5, 7) → 9660 (2^2, 3, 5, 7, 23)
4002 → 2004 (base=11)
5326 (2, 2663) → 2666 (2, 31, 43)
13772 → 27731 (base=11)
19560 (2^3, 3, 5, 163) → 39480 (2^3, 3, 5, 7, 47)
4[10]7[10]9 → 9[10]7[10]4 (base=11)
72840 (2^3, 3, 5, 607) → 146040 (2^3, 3, 5, 1217)
6929[10] → [10]9296 (base=11)
100176 (2^4, 3, 2087) → 158736 (2^4, 3, 3307)
171623 → 326171 (base=11)
265620 (2^2, 3, 5, 19, 233) → 520620 (2^2, 3, 5, 8677)
263702 → 207362 (base=11)
414790 (2, 5, 41479) → 331850 (2, 5^2, 6637)

Note that 42 mirrors its factor-sum in both base-9 and base-11. But s(42) = 24 in infinitely many bases, because when 42 = 2 x prime, s(42) = 1 + 2 + prime. So (prime-1) / 2 will give the base in which 24 = s(42). For example, 2 x 11 = 22 and 22 = 42 in base (11-1) / 2 or base-5. So s(42) = 1 + 2 + 11 = 14 = 2 x 5 + 4 = 24[b=5]. There are infinitely many primes, so infinitely many bases in which s(42) = 24.

Base-10 does better for mirror-sums when s(n) is re-defined to include n itself. So s(69) = 1 + 3 + 23 + 69 = 96. Here are the first examples of all-factor mirror-sums in base-10:

69 (3, 23) → 96 (2^5, 3)
276 (2^2, 3, 23) → 672 (2^5, 3, 7)
639 (3^2, 71) → 936 (2^3, 3^2, 13)
2556 (2^2, 3^2, 71) → 6552 (2^3, 3^2, 7, 13)

In the same range, base-9 now produces one mirror-sum, 13 → 31 = 12 (2^2, 3) → 28 (2^2, 7). Base-11 produces no mirror-sums in the same range. Base behaviour is eccentric, but that’s what makes it interesting.

Back to Bases

by in Mathematics and tagged , , , , , , , , , , , , , | Leave a comment

(N.B. I am not a mathematician and often make stupid mistakes in my recreational maths. Caveat lector.)

101 isn’t a number, it’s a label for a number. In fact, it’s a label for infinitely many numbers. In base 2, 1012 = 5; in base 3, 1013 = 10; 1014 = 17; 1015 = 26; and so on, for ever. In some bases, like 2 and 4, the number labelled 101 is prime. In other bases, it isn’t. But it is always a palindrome: that is, it’s the same read forward and back. But 101, the number itself, is a palindrome in only two bases: base 10 and base 100.1 Note that 100 = 101-1: with the exception of 2, all integers, or whole numbers, are palindromic in at least one base, the base that is one less than the integer itself. So 3 = 112; 4 = 113; 5 = 114; 101 = 11100; and so on.

Less trivial is the question of which integers set progressive records for palindromicity, or for the number of palindromes they create in bases less than the integers themselves. You might guess that the bigger the integer, the more palindromes it will create, but it isn’t as simple as that. Here is 10 represented in bases 2 through 9:

10102 | 1013* | 224* | 205 | 146 | 137 | 128 | 119*

10 is a palindrome in bases 3, 4, and 9. Now here is 30 represented in bases 2 through 29 (note that a number between square brackets represents a single digit in that base):2

111102 | 10103 | 1324 | 1105 | 506 | 427 | 368 | 339* | 30 | 2811 | 2612 | 2413 | 2214* | 2015 | 1[14]16 | 1[13]17 | 1[12]18 | 1[11]19 | 1[10]20 | 1921 | 1822 | 1723 | 1624 | 1525 | 1426 | 1327 | 1228
| 1129*

30, despite being three times bigger than 10, creates only three palindromes too: in bases 9, 14, and 29. Here is a graph showing the number of palindromes for each number from 3 to 100 (prime numbers are in red):

Graph of palindromes in various bases for n=3 to 100

The number of palindromes a number has is related to the number of factors, or divisors, it has. A prime number has only one factor,  itself (and 1), so primes tend to be less palindromic than composite numbers. Even large primes can have only one palindrome, in the base b=n-1 (55,440 has 119 factors and 61 palindromes; 65,381 has one factor and one palindrome, 1165380). Here is a graph showing the number of factors for each number from 3 to 100:

Graph of number of factors for n = 3 to 100

And here is an animated gif combining the two previous images:

Animated gif of number of palindromes and factors, n=3 to 100

Here is a graph indicating where palindromes appear when n, along the x-axis, is represented in the bases b=2 to n-1, along the y-axis:

Graph showing where palindromes occur in various bases for n = 3 to 1000

The red line are the palindromes in base b=n-1, which is “11” for every n>2. The lines below it arise because every sufficiently large n with divisor d can be represented in the form d·n1 + d. For example, 8 = 2·3 + 2, so 8 in base 3 = 223; 18 = 3·5 + 3, so 18 = 335; 32 = 4.7 + 4, so 32 = 447; 391 = 17·22 + 17, so 391 = [17][17]22.

And here, finally, is a table showing integers that set progressive records for palindromicity (p = number of palindromes, f = total number of factors, prime and non-prime):

n Prime Factors p f    n Prime Factors p f
3 3 1 1    2,520 23·32·5·7 25 47
5 5 2 1    3,600 24·32·52 26 44
10 2·5 3 3    5,040 24·32·5·7 30 59
21 3·7 4 3    7,560 23·33·5·7 32 63
36 22·32 5 8    9,240 23·3·5·7·11 35 63
60 22·3·5 6 11    10,080 25·32·5·7 36 71
80 24·5 7 9    12,600 23·32·52·7 38 71
120 23·3·5 8 15    15,120 24·33·5·7 40 79
180 22·32·5 9 17    18,480 24·3·5·7·11 43 79
252 22·32·7 11 17    25,200 24·32·52·7 47 89
300 22·3·52 13 17    27,720 23·32·5·7·11 49 95
720 24·32·5 16 29    36,960 25·3·5·7·11 50 95
1,080 23·33·5 17 31    41,580 22·33·5·7·11 51 95
1,440 25·32·5 18 35    45,360 24·34·5·7 52 99
1,680 24·3·5·7 20 39    50,400 25·32·52·7 54 107
2,160 24·33·5 21 39    55,440 24·32·5·7·11 61 119

Notes

1. That is, it’s only a palindrome in two bases less than 101. In higher bases, “101” is a single digit, so is trivially a palindrome (as the numbers 1 through 9 are in base 10).

2. In base b, there are b digits, including 0. So base 2 has two digits, 0 and 1; base 10 has ten digits, 0-9; base 16 has sixteen digits: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F.