Tag Archives: fractal animation

Trigging Triangles

by in Fractals, Geometry, Mathematics, Triangles and tagged , , , , , , , , , , | Leave a comment

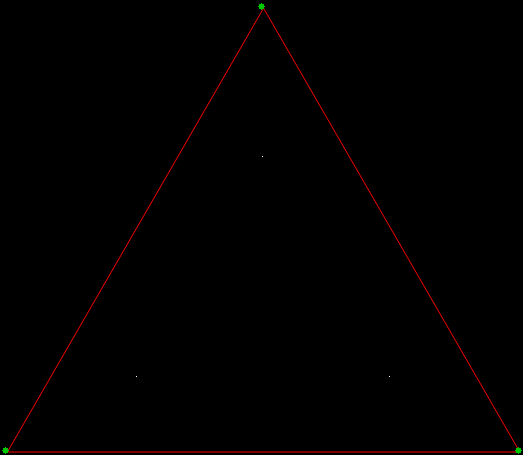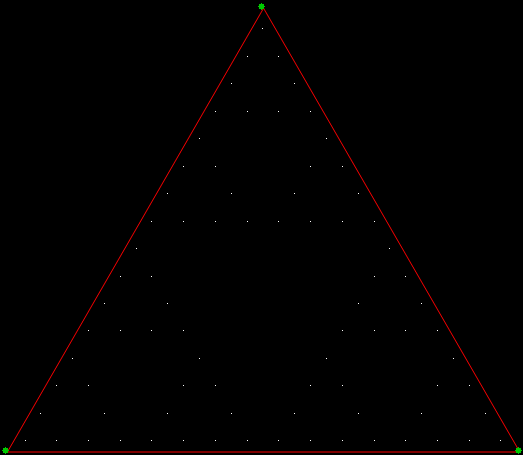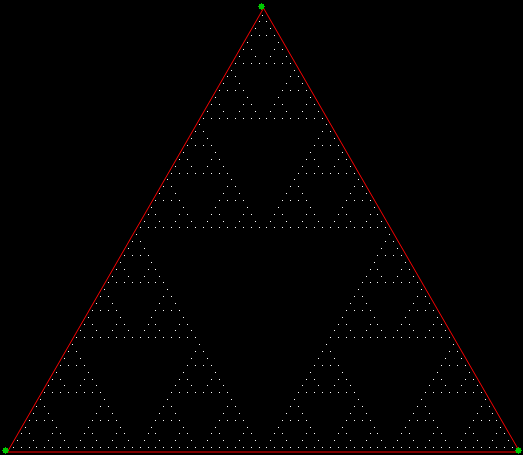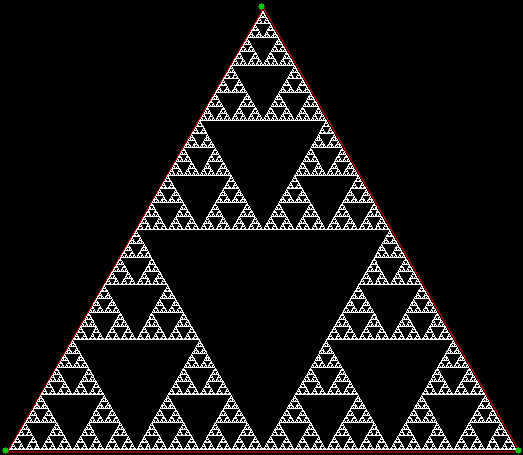
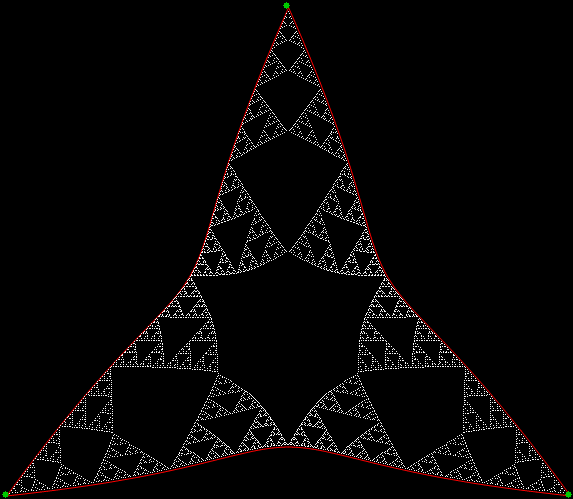
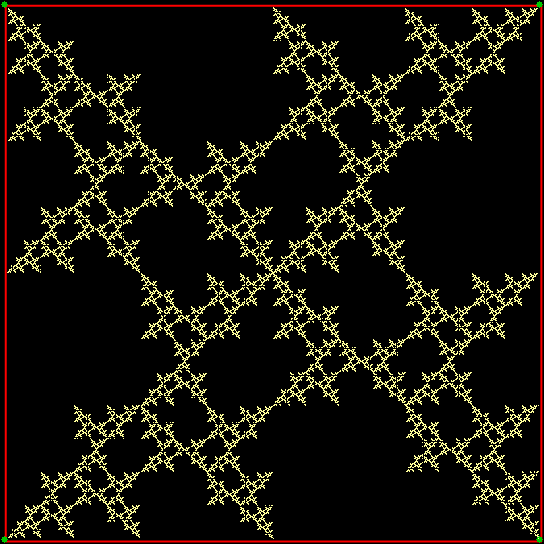
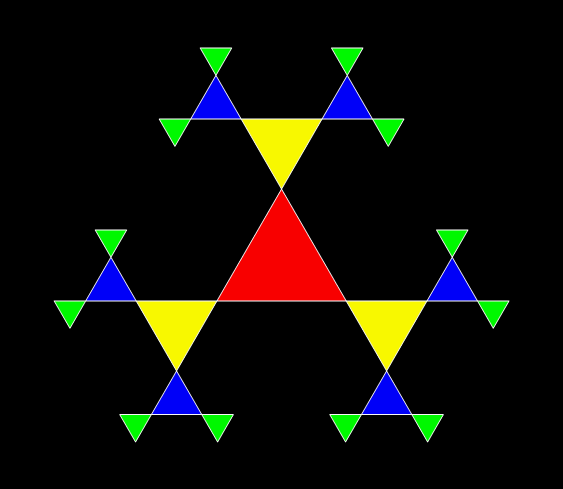
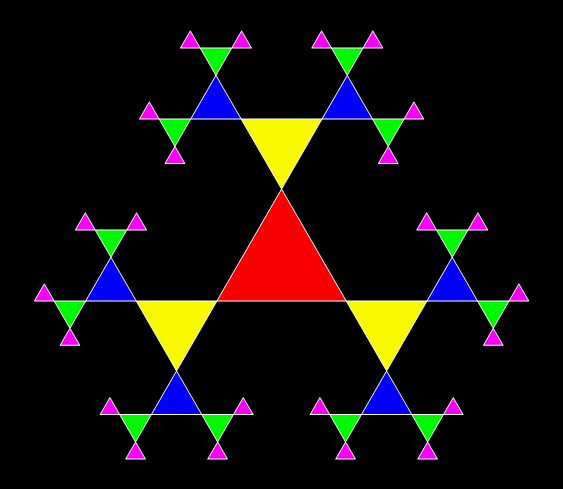
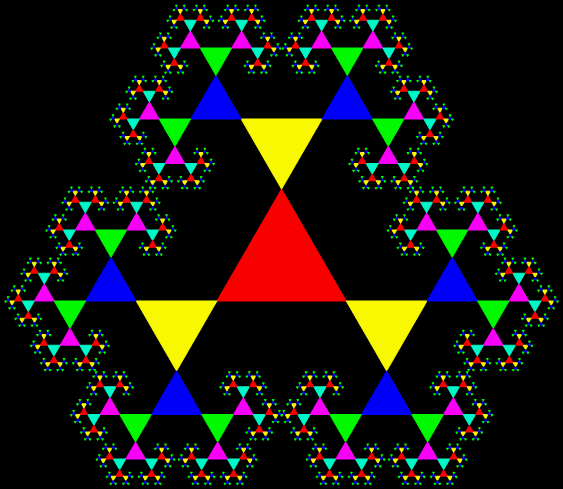
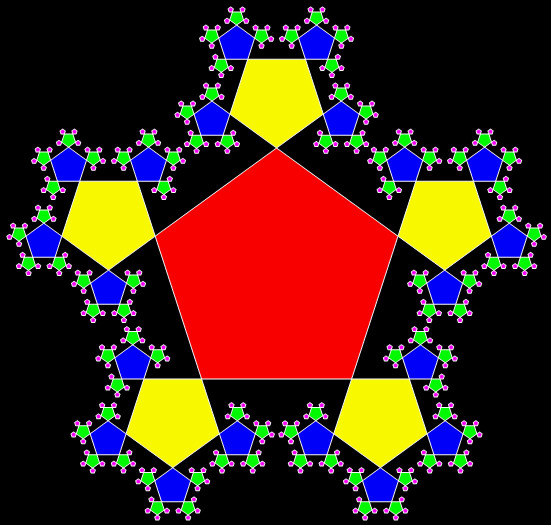
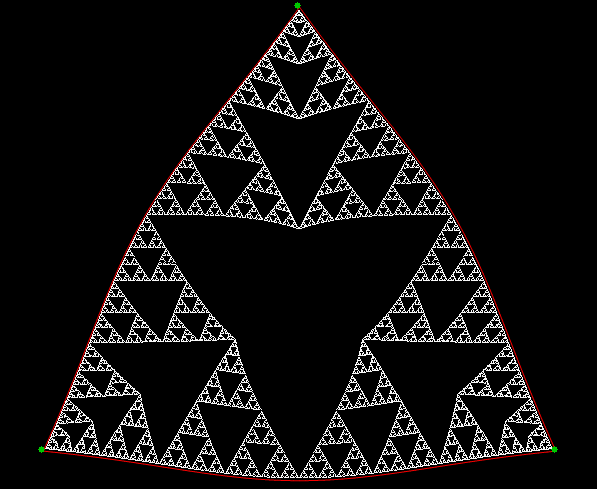A fractal is a shape in which a part looks like the whole. Trees are fractals. And lungs. And clouds. But there are man-made fractals too and probably the most famous of them all is the Sierpiński triangle, invented by the Polish mathematician Wacław Sierpiński (1882-1969):

Sierpiński triangle

There are many ways to create a Sierpiński triangle, but one of the simplest is to trace all possible routes followed by a point jumping halfway towards the vertices of an equilateral triangle. If you mark the endpoint of the jumps, the Sierpiński triangle appears as the routes get longer and longer, like this:

Point jumping 1/2 way towards vertices of an equilateral triangle (animated)

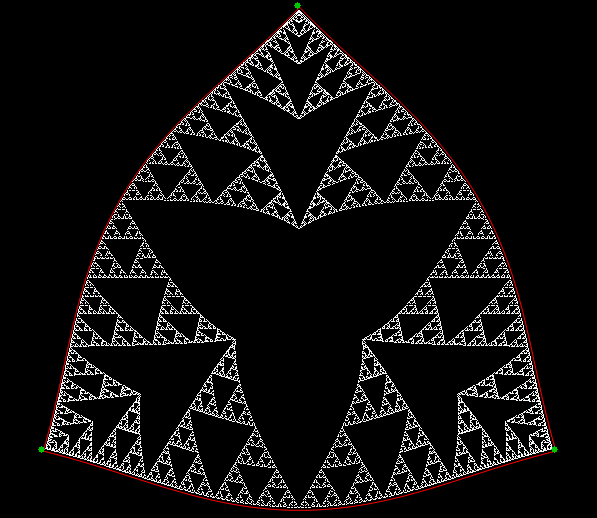
Once you’ve created a Sierpiński triangle like that, you can play with it. For example, you can use simple trigonometry to stretch the triangle into a circle:

Sierpiński triangle to circle stage #1

Sierpiński triangle to circle #2

Sierpiński triangle to circle #3

Sierpiński triangle to circle #4

Sierpiński triangle to circle #5

Sierpiński triangle to circle #6

Sierpiński triangle to circle #7

Sierpiński triangle to circle #8

Sierpiński triangle to circle #9

Sierpiński triangle to circle #10

Sierpiński triangle to Sierpiński circle (animated)

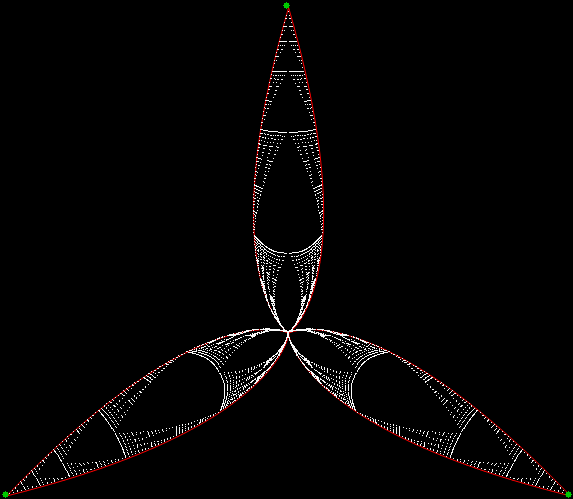
But the trigging of the triangle can go further. You can expand the Sierpiński circle further, like this:

Sierpiński circle expanded

Or shrink the Sierpiński triangle like this:

Shrinking Sierpiński triangle stage #1

Shrinking Sierpiński triangle #2

Shrinking Sierpiński triangle #3

Shrinking Sierpiński triangle #4

Shrinking Sierpiński triangle #5

Shrinking Sierpiński triangle #6

Shrinking Sierpiński triangle (animated)

You can also create new shapes using the jumping-point technique. Suppose that, as the point is jumping, you adjust its position outwards into the circumscribed circle whenever it lands within the boundaries of the governing triangle. But if the point lands outside those boundaries, you leave it alone. Using this adapted technique, you get a shape like this:

Adjusted Sierpiński circle

And if the point is swung by 60° after it’s adjusted into the circle, you get a shape like this:

Adjusted Sierpiński circle (60° swing)

Here are some animated gifs showing these shapes rotating in a full circle at various speeds:

Adjusted Sierpiński circle (swinging animation) (fast)

Adjusted Sierpiński circle (swinging animation) (medium)

Adjusted Sierpiński circle (swinging animation) (slow)

Arty Fish Haul

by in Fractals, Mathematics, Triangles and tagged , , , , , , , , | Leave a comment

When is a fish a reptile? When it looks like this:

Fish from four isosceles right triangles

The fish-shape can be divided into eight identical sub-copies of itself. That is, it can be repeatedly tiled with copies of itself, so it’s an example of what geometry calls a rep-tile:

Fish divided into eight identical sub-copies

Fish divided again

Fish divided #4

Fish divided #5

Fish divided #6

Fish (animated rep-tiling)

Now suppose you divide the fish, then discard one of the sub-copies. And carry on dividing-and-discarding like that:

Fish discarding sub-copy 7 (#1)

Fish discarding sub-copy 7 (#2)

Fish discarding sub-copy 7 (#3)

Fish discarding sub-copy 7 (#4)

Fish discarding sub-copy 7 (#5)

Fish discarding sub-copy 7 (#6)

Fish discarding sub-copy 7 (#7)

Fish discarding sub-copy 7 (animated)

Here are more examples of the fish sub-dividing, then discarding sub-copies:

Fish discarding sub-copy #1

Fish discarding sub-copy #2

Fish discarding sub-copy #3

Fish discarding sub-copy #4

Fish discarding sub-copy #5

Fish discarding sub-copy #6

Fish discarding sub-copy #7

Fish discarding sub-copy #8

Fish discarding sub-copies (animated)

Now try a square divided into four copies of the fish, then sub-divided again and again:

Fish-square #1

Fish-square #2

Fish-square #3

Fish-square #4

Fish-square #5

Fish-square #6

Fish-square (animated)

The fish-square can be used to create more symmetrical patterns when the divide-and-discard rule is applied. Here’s the pattern created by dividing-and-discarded two of the sub-copies:

Fish-square divide-and-discard #1

Fish-square divide-and-discard #2

Fish-square divide-and-discard #3

Fish-square divide-and-discard #4

Fish-square divide-and-discard #5

Fish-square divide-and-discard #6

Fish-square divide-and-discard #7

Fish-square divide-and-discard #8 (delayed discard)

Fish-square divide-and-discard (animated)

Using simple trigonometry, you can convert the square pattern into a circular pattern:

↓

Circular version

Square to circle (animated)

Here are more examples of divide-and-discard fish-squares:

Fish-square divide-and-discard #1

Fish-square divide-and-discard #2

Fish-square divide-and-discard #3

Fish-square divide-and-discard #4

Fish-square divide-and-discard #5

Fish-square divide-and-discard #6

And more examples of fish-squares being converted into circles:

Fish-square to circle #1 (animated)

Fish-square to circle #2

Fish-square to circle #3

Fish-square to circle #4

Fish-square to circle #5

Fish-square to circle #6

Square Routes Re-Re-Re-Re-Re-Re-Revisited

by in Fractals, Geometry, Mathematics, Pentagons, Polygons, Squares, Triangles and tagged , , , , , , , , | Leave a comment

Suppose you trace all possible routes followed by a point inside a triangle jumping halfway towards one or another of the three vertices of the triangle. If you mark each jump, you get a famous geometrical shape called the Sierpiński triangle (or Sierpiński sieve).

Sierpiński triangle found by tracing all possible routes for a point jumping halfway towards the vertices of a triangle

The Sierpiński triangle is a fractal, because it contains copies of itself at smaller and smaller scales. Now try the same thing with a square. If you trace all possible routes followed by a point inside a square jumping halfway towards one or another of the four vertices of the square, you don’t get an obvious fractal. Instead, the interior of the square fills steadily (and will eventually be completely solid):

Routes of a point jumping halfway towards vertices of a square

Try a variant. If the point is banned from jumping towards the same vertex twice or more in a row, the routes trace out a fractal that looks like this:

Ban on choosing same vertex twice or more in a row

If the point is banned from jumping towards the vertex one place anti-clockwise of the vertex it’s just jumped towards, you get a fractal like this:

Ban on jumping towards vertex one place anti-clockwise of previously chosen vertex

And if the point can’t jump towards two places clockwise or anti-clockwise of the currently chosen vertex, this fractal appears (called a T-square fractal):

Ban on jumping towards the vertex diagonally opposite of the previously chosen vertex

That ban is equivalent to banning the point from jumping from the vertex diagonally opposite to the vertex it’s just jumped towards. Finally, here’s the fractal created when you ban the point from jumping towards the vertex one place clockwise of the vertex it’s just jumped towards:

Ban on jumping towards vertex one place clockwise of previously chosen vertex

As you can see, the fractal is a mirror-image of the one-place-anti-clockwise-ban fractal.

I discovered the ban-construction of those fractals more than twenty years ago. Then I found that I was re-discovering the same fractals when I looked at what first seemed like completely different ways of constructing fractals. There are lots of different routes to the same result. I’ve recently discovered yet another route. Let’s try what seems like an entirely different way of constructing fractals. Take a square and erect four new half-sized squares, sq1, sq2, sq3, sq4, on each corner. Then erect three more quarter-sized squares on the outward facing corners of sq1, sq2, sq3 and sq4. Carry on doing that and see what happens at the end when you remove all the previous stages of construction:

Animation of the new construction

Animation in black-and-white

It’s the T-square fractal again. Now try rotating the squares you add at stage 3 and see what happens (the rotation means that two new squares are added on adjacent outward-facing corners and one new square on the inward-facing corner):

Animation of the construction

It’s the one-place-clockwise-ban fractal again. Now try rotating the squares two places, so that two new squares are added on diagonally opposite outward-facing corners and one new square on the inward-facing corner:

Animation of the construction

It’s the same-vertex-ban fractal again. Finally, rotate squares one place more:

Animation of the construction

It’s the one-place-clockwise-ban fractal again. And this method isn’t confined to squares. Here’s what happens when you add 5/8th-sized triangles to the corners of triangles:

Animation of the construction

And here’s what happens when you add 5/13th-sized pentagons to the corners of pentagons:

Animation of the construction

Finally, here’s a variant on that pentagonal fractal (adding two rather than four pentagons at stage 3 and higher):

Animation of the construction

Previously pre-posted (please peruse):

• Square Routes
• Square Routes Revisited
• Square Routes Re-Revisited
• Square Routes Re-Re-Revisited
• Square Routes Re-Re-Re-Revisited
• Square Routes Re-Re-Re-Re-Revisited
• Square Routes Re-Re-Re-Re-Re-Revisited