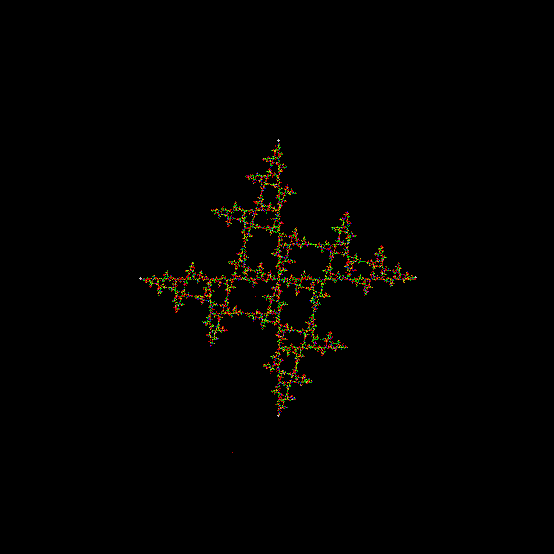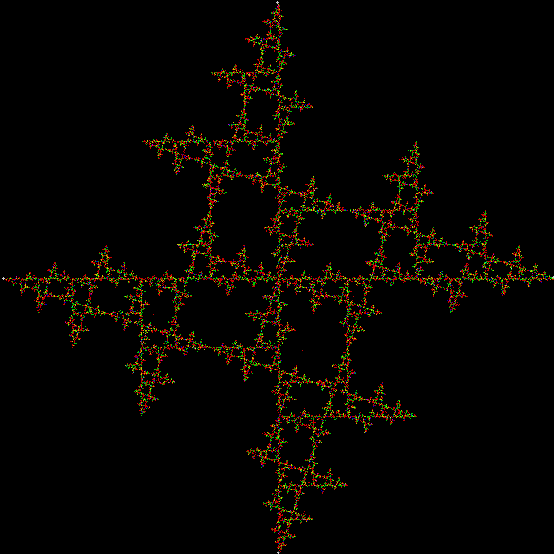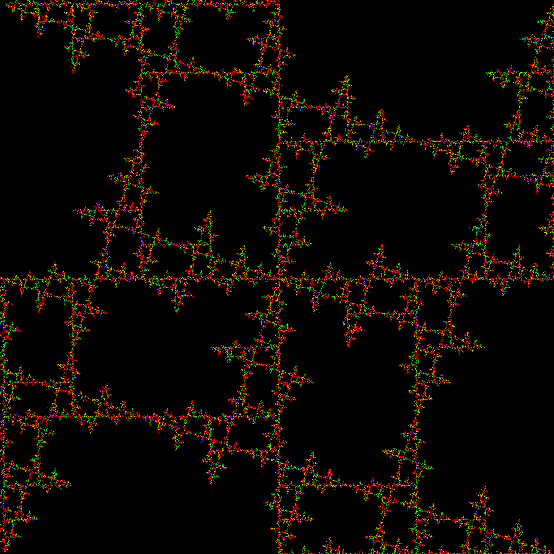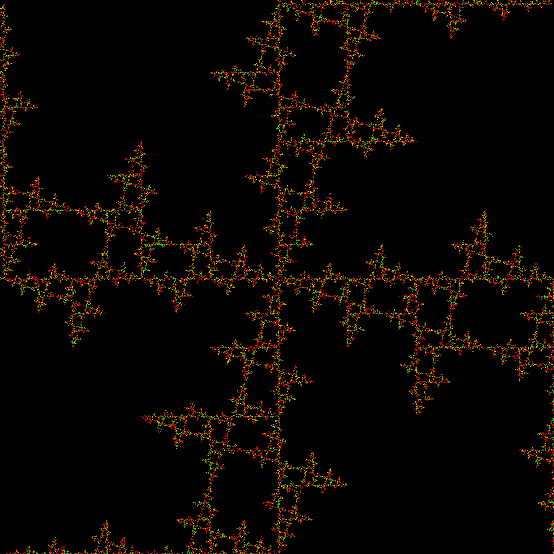
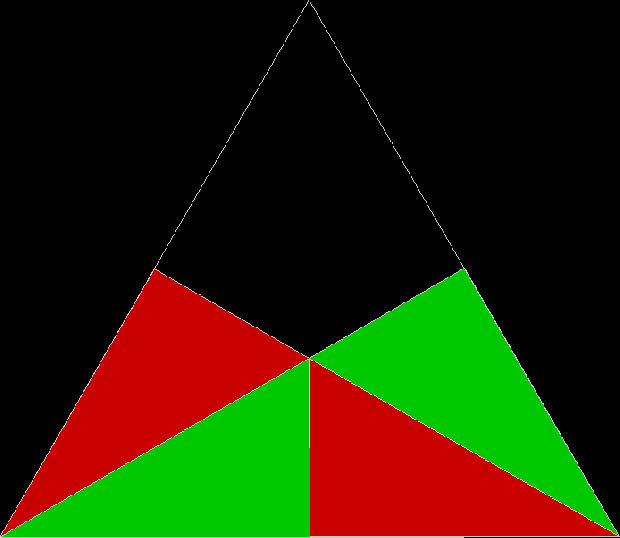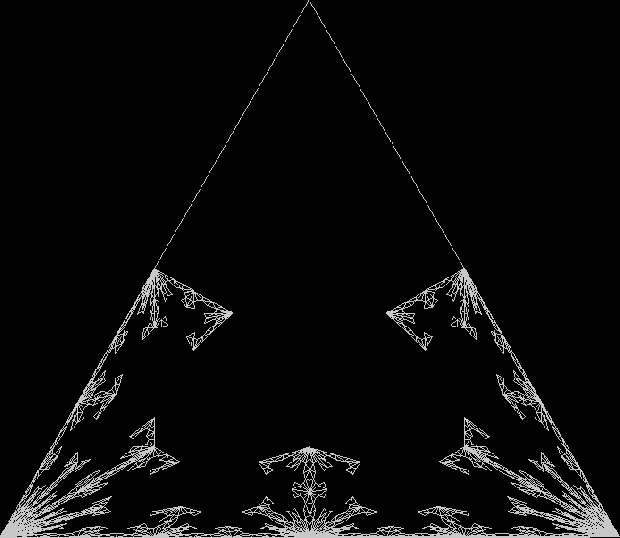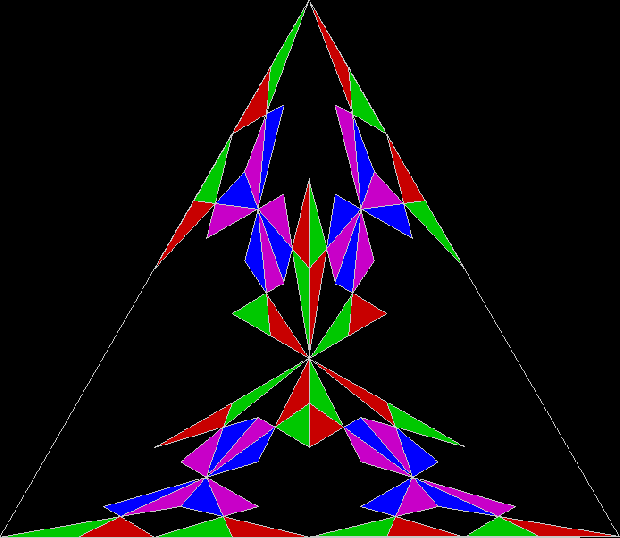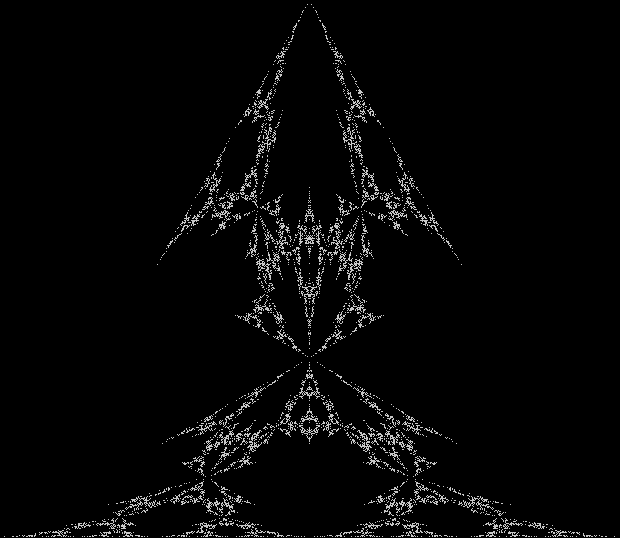
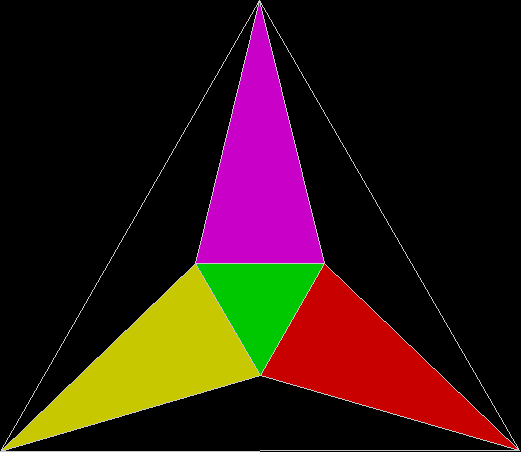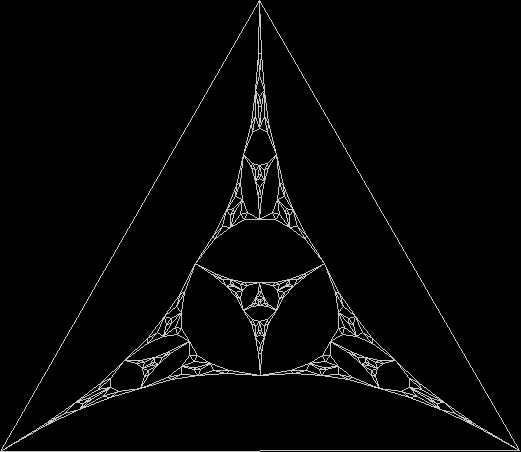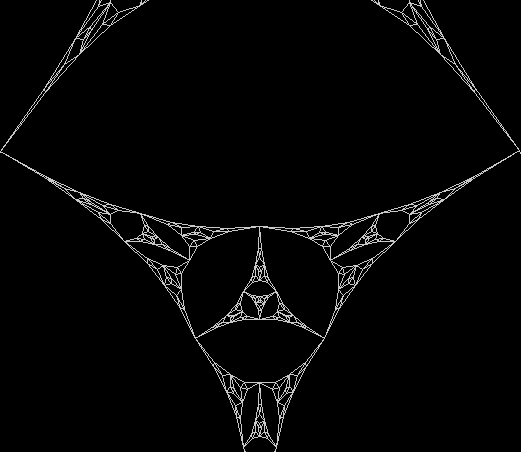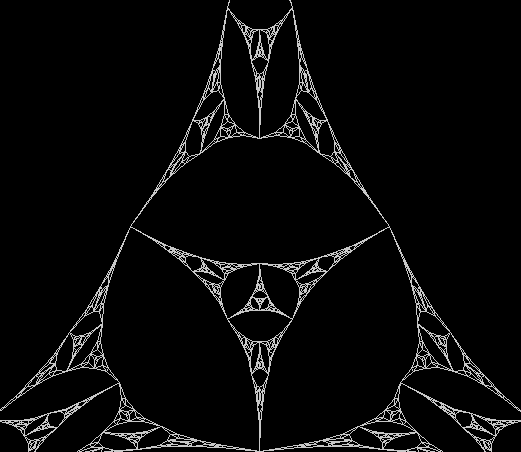
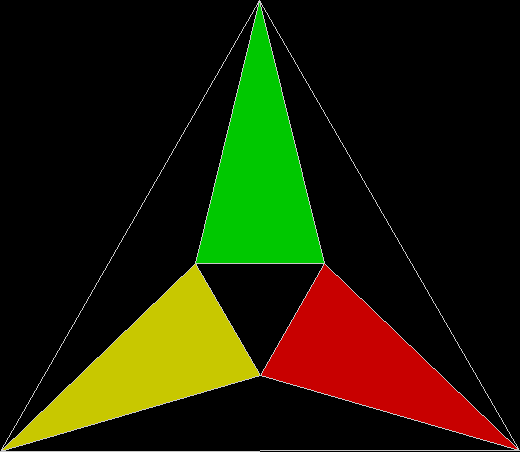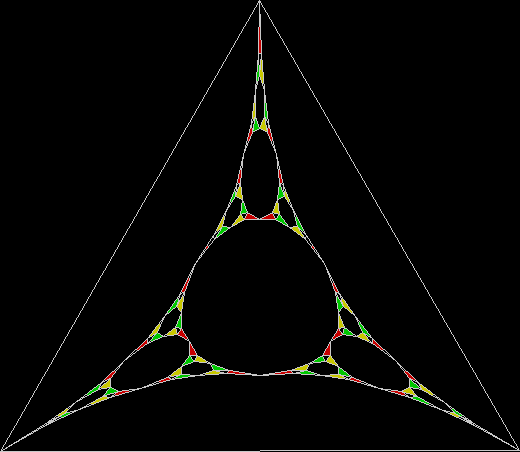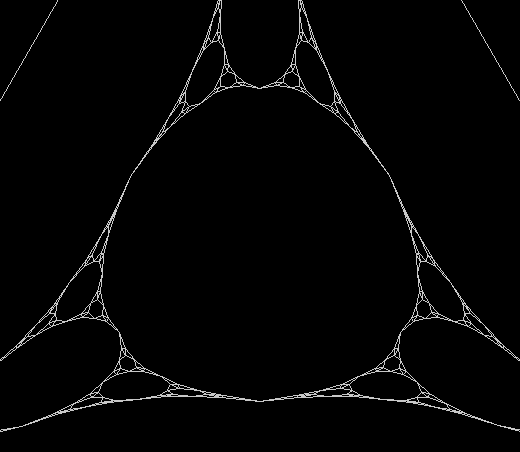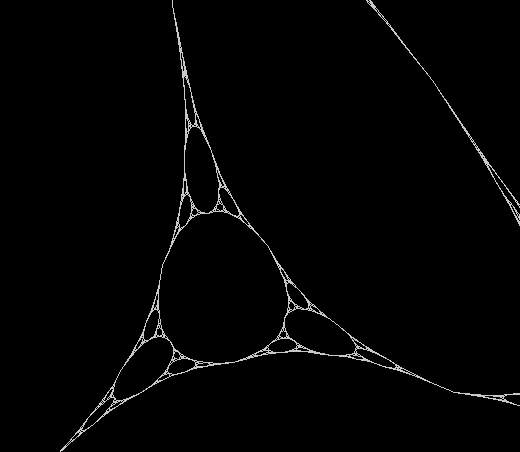
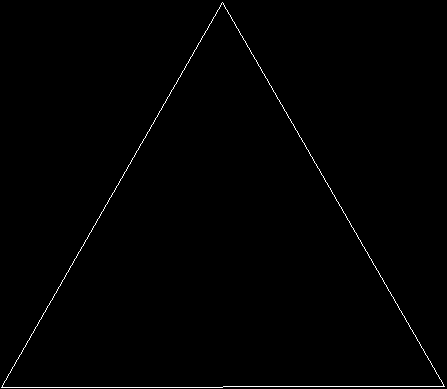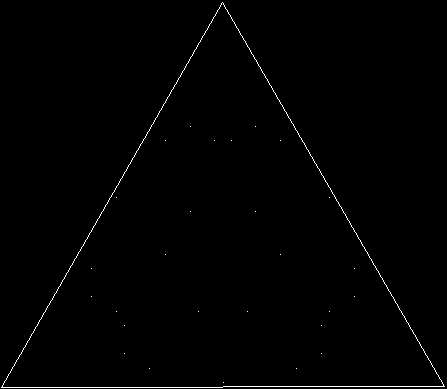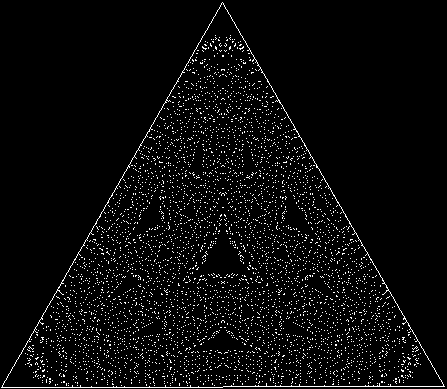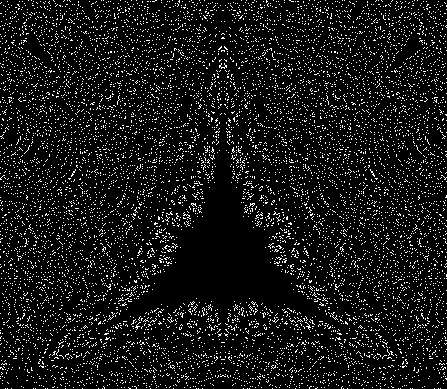
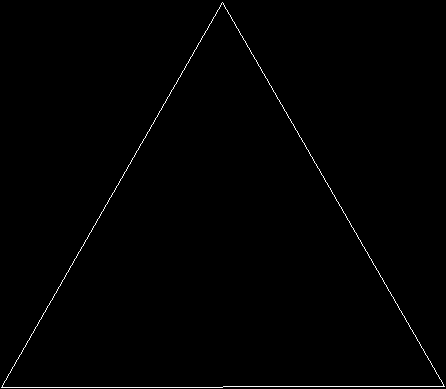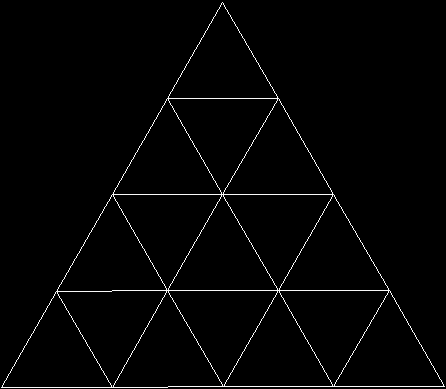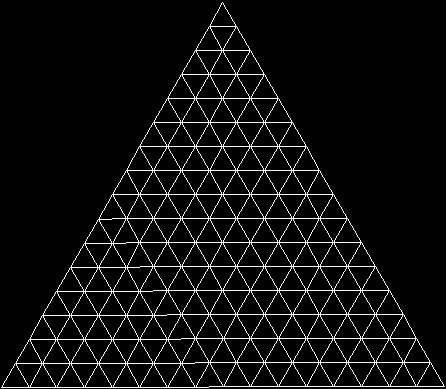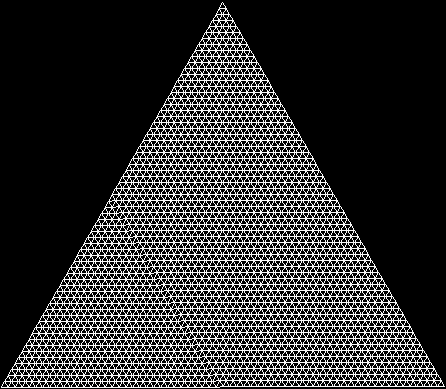
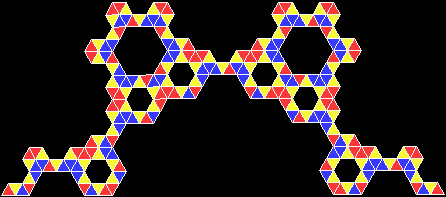
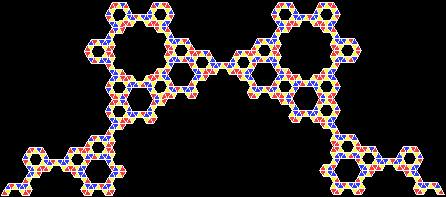
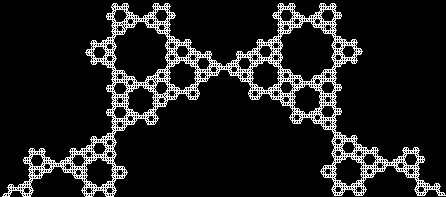
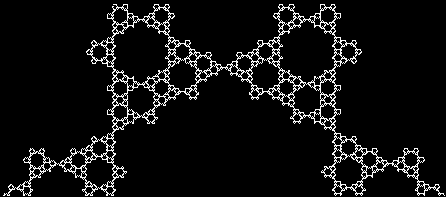
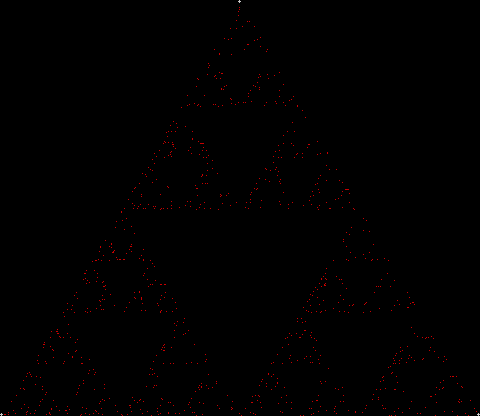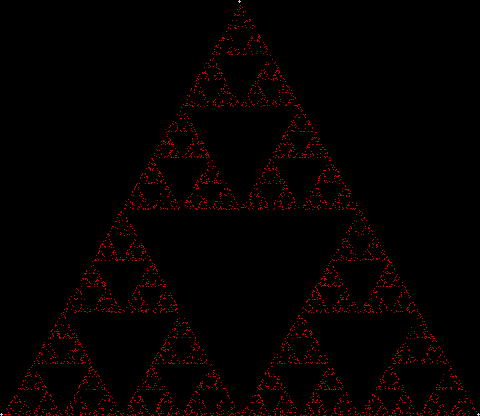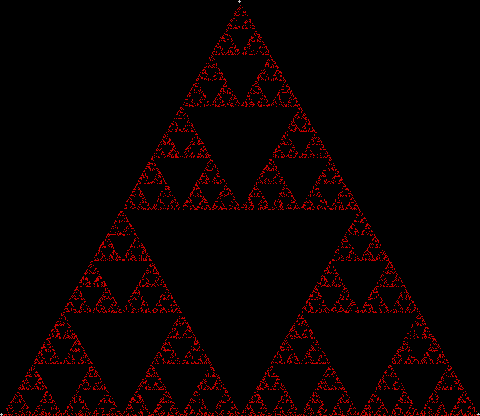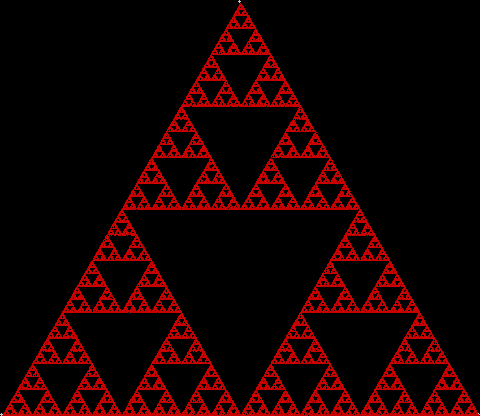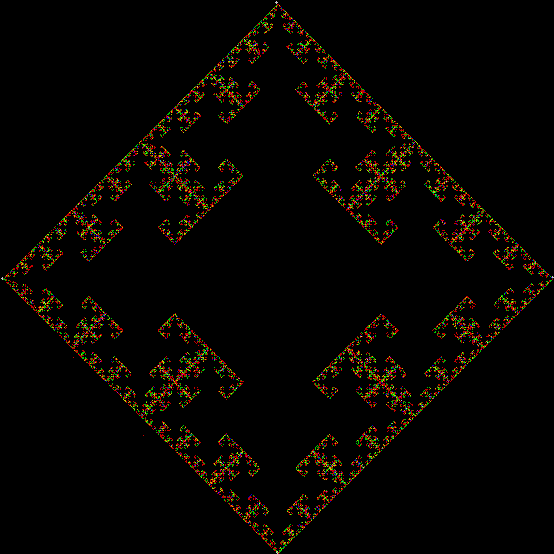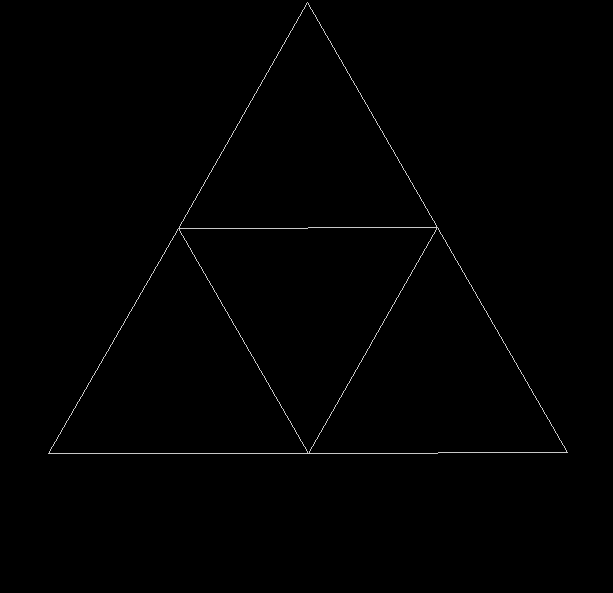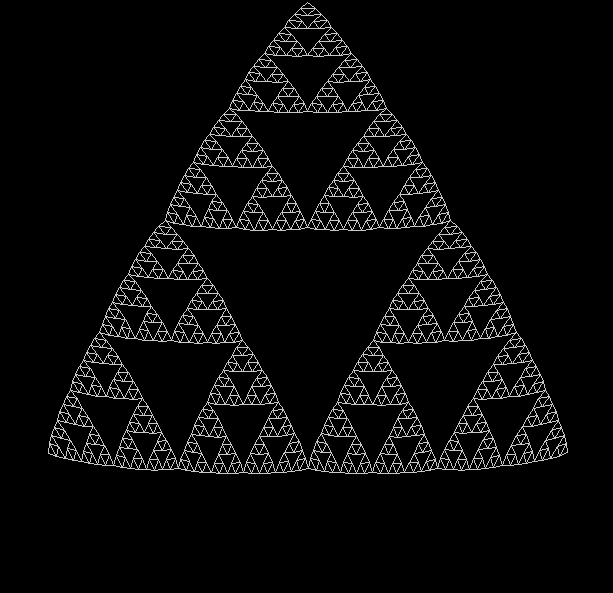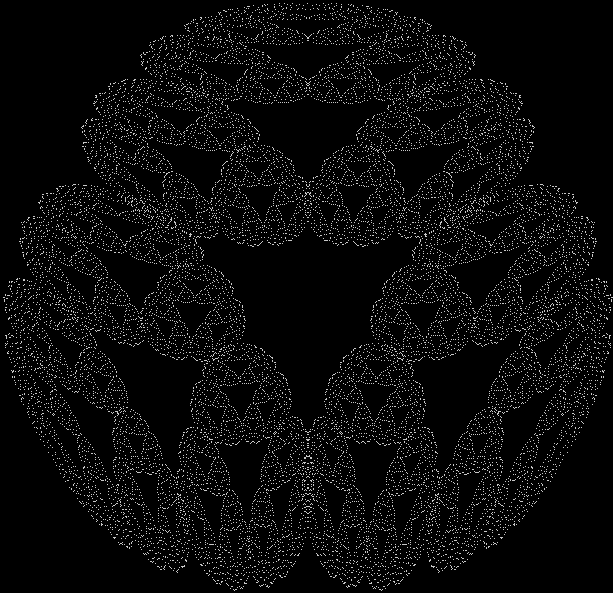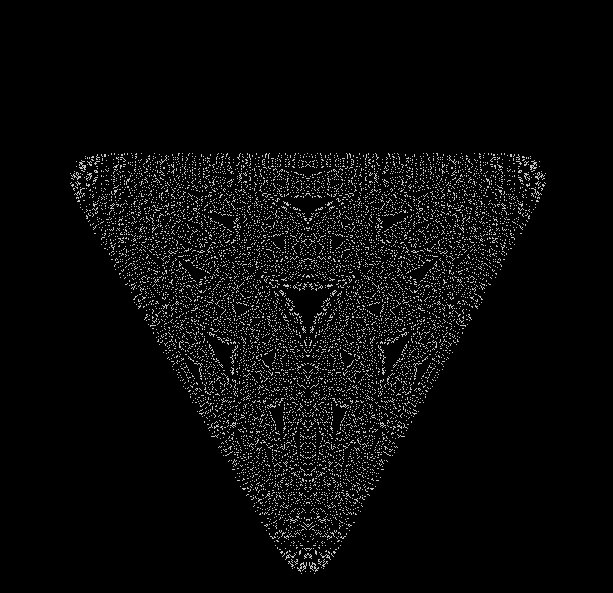To create a simple fractal, take an equilateral triangle and divide it into four more equilateral triangles. Remove the middle triangle. Repeat the process with each new triangle and go on repeating it. You’ll end up with a shape like this, which is known as the Sierpiński triangle, after the Polish mathematician Wacław Sierpiński (1882-1969):
But you can also create the Sierpiński triangle one pixel at a time. Choose any point inside an equilateral triangle. Pick a corner of the triangle at random and move half-way towards it. Mark this spot. Then pick a corner at random again and move half-way towards the corner. And repeat. The result looks like this:
A simple program to create the fractal looks like this:
initial()
repeat
fractal()
altervariables()
until falsefunction initial()
v = 3 [v for vertex]
r = 500
lm = 0.5
endfuncfunction fractal()
th = 2 * pi / v
[the following loop creates the corners of the triangle]
for l = 1 to v
x[l]=xcenter + sin(l*th) * r
y[l]=ycenter + cos(l*th) * r
next l
fx = xcenter
fy = ycenter
repeat
rv = random(v)
fx = fx + (x[rv]-fx) * lm
fy = fy + (y[rv]-fy) * lm
plot(fx,fy)
until keypressed
endfuncfunction altervariables()
[change v, lm, r etc]
endfunc
In this case, more is less. When v = 4 and the shape is a square, there is no fractal and plot(fx,fy) covers the entire square.
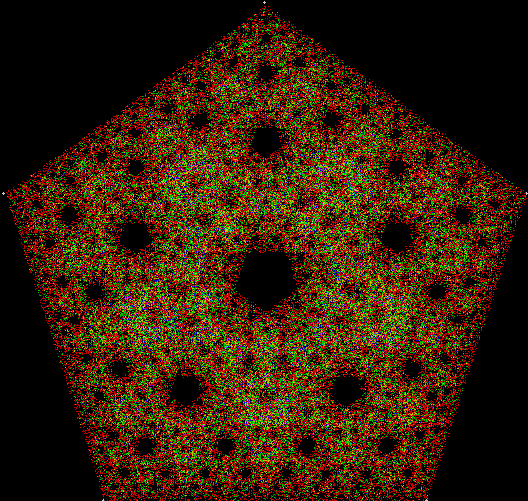
When v = 5 and the shape is a pentagon, this fractal appears:
But v = 4 produces a fractal if a simple change is made in the program. This time, a corner cannot be chosen twice in a row:
function initial()
v = 4
r = 500
lm = 0.5
ci = 1 [i.e, number of iterations since corner previously chosen]
endfuncfunction fractal()
th = 2 * pi / v
for l = 1 to v
x[l]=xcenter + sin(l*th) * r
y[l]=ycenter + cos(l*th) * r
chosen[l]=0
next l
fx = xcenter
fy = ycenter
repeat
repeat
rv = random(v)
until chosen[rv]=0
for l = 1 to v
if chosen[l]>0 then chosen[l] = chosen[l]-1
next l
chosen[rv] = ci
fx = fx + (x[rv]-fx) * lm
fy = fy + (y[rv]-fy) * lm
plot(fx,fy)
until keypressed
endfunc
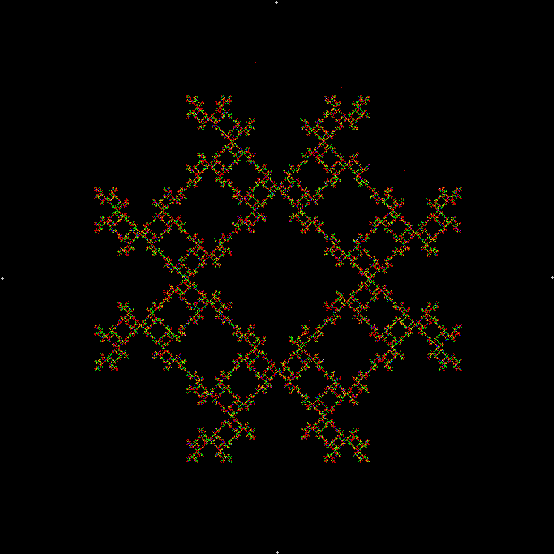
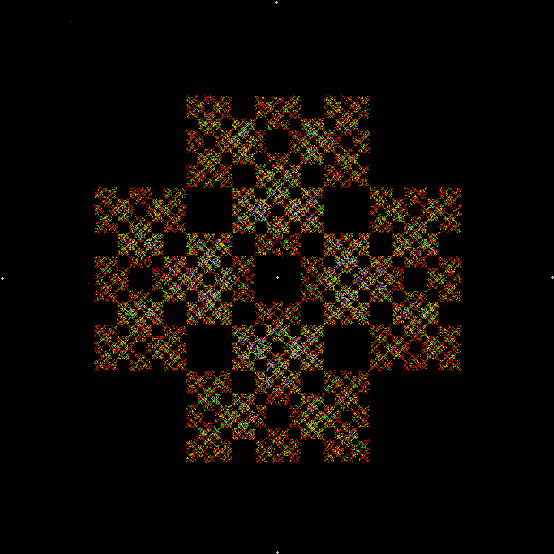
One can also disallow a corner if the corner next to it has been chosen previously, adjust the size of the movement towards the chosen corner, add a central point to the polygon, and so on. Here are more fractals created with such variations: