Author Archives: Krilling for Company

Look with Luther

by in Quotations, Translation and tagged , , , , | Leave a comment

Denn in der wahren Natur der Dinge ist, wenn wir recht bedenken, jeder grüne Baum viel herrlicher, als wenn er aus Gold und Silber wäre. — Martin Luther

• “For in the true nature of things, if we rightly consider, every green tree is far more glorious than if it were made of gold and silver.”

Post-Performative Post-Scriptum

I’ve tried to find where — and indeed if — Luther originally wrote this but can’t find anything but “Inspirational Quotes” pages. And some of those attribute it to Martin Luther King. It doesn’t sound like MLK to me and the German doesn’t look translated from English. It’s a good quote whoever first said it and whatever language it was first said in.

Fabulous Furry Fibonacci Fractal

by in Arithmetic, Fibonacci Sequence, Fractals, Integer Sequences, Mathematics and tagged , , , , , , , , | Leave a comment

At least, I think it’s a fractal. I came across it when I was counting the ways in which the integers can be the sum of distinct Fibonacci numbers. Here for reference is the Fibonacci sequence, the beautiful and endlessly fertile sequence that’s seeded with “1, 1” and continued by summing the two previous numbers:

1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946, 17711, 28657, 46368, 75025, 121393, 196418, 317811, 514229, 832040…

I noticed some interesting patterns in the distinct-fib-num-sum count for the integers:

1 = 1 (count=1)
2 = 2 (count=1)
3 = 1+2 = 3 (count=2)
4 = 1+3 (c=1)
5 = 2+3 = 5 (c=2)
6 = 1+2+3 = 1+5 (c=2)
7 = 2+5 (c=1)
8 = 1+2+5 = 3+5 = 8 (c=3)
9 = 1+3+5 = 1+8 (c=2)
10 = 2+3+5 = 2+8 (c=2)
11 = 1+2+3+5 = 1+2+8 = 3+8 (c=3)
12 = 1+3+8 (c=1)
13 = 2+3+8 = 5+8 = 13 (c=3)
14 = 1+2+3+8 = 1+5+8 = 1+13 (c=3)
15 = 2+5+8 = 2+13 (c=2)
16 = 1+2+5+8 = 3+5+8 = 1+2+13 = 3+13 (c=4)
17 = 1+3+5+8 = 1+3+13 (c=2)
18 = 2+3+5+8 = 2+3+13 = 5+13 (c=3)
19 = 1+2+3+5+8 = 1+2+3+13 = 1+5+13 (c=3)
20 = 2+5+13 (c=1)
21 = 1+2+5+13 = 3+5+13 = 8+13 = 21 (c=4)
22 = 1+3+5+13 = 1+8+13 = 1+21 (c=3)
23 = 2+3+5+13 = 2+8+13 = 2+21 (c=3)
24 = 1+2+3+5+13 = 1+2+8+13 = 3+8+13 = 1+2+21 = 3+21 (c=5)
25 = 1+3+8+13 = 1+3+21 (c=2)
26 = 2+3+8+13 = 5+8+13 = 2+3+21 = 5+21 (c=4)
27 = 1+2+3+8+13 = 1+5+8+13 = 1+2+3+21 = 1+5+21 (c=4)
28 = 2+5+8+13 = 2+5+21 (c=2)
29 = 1+2+5+8+13 = 3+5+8+13 = 1+2+5+21 = 3+5+21 = 8+21 (c=5)
30 = 1+3+5+8+13 = 1+3+5+21 = 1+8+21 (c=3)
31 = 2+3+5+8+13 = 2+3+5+21 = 2+8+21 (c=3)
32 = 1+2+3+5+8+13 = 1+2+3+5+21 = 1+2+8+21 = 3+8+21 (c=4)
33 = 1+3+8+21 (c=1)
34 = 2+3+8+21 = 5+8+21 = 13+21 = 34 (c=4)
35 = 1+2+3+8+21 = 1+5+8+21 = 1+13+21 = 1+34 (c=4)
36 = 2+5+8+21 = 2+13+21 = 2+34 (c=3)
37 = 1+2+5+8+21 = 3+5+8+21 = 1+2+13+21 = 3+13+21 = 1+2+34 = 3+34
(c=6)
38 = 1+3+5+8+21 = 1+3+13+21 = 1+3+34 (c=3)
39 = 2+3+5+8+21 = 2+3+13+21 = 5+13+21 = 2+3+34 = 5+34 (c=5)
40 = 1+2+3+5+8+21 = 1+2+3+13+21 = 1+5+13+21 = 1+2+3+34 = 1+5+34
(c=5)
41 = 2+5+13+21 = 2+5+34 (c=2)
42 = 1+2+5+13+21 = 3+5+13+21 = 8+13+21 = 1+2+5+34 = 3+5+34 = 8+3
4 (c=6)
43 = 1+3+5+13+21 = 1+8+13+21 = 1+3+5+34 = 1+8+34 (c=4)
44 = 2+3+5+13+21 = 2+8+13+21 = 2+3+5+34 = 2+8+34 (c=4)
45 = 1+2+3+5+13+21 = 1+2+8+13+21 = 3+8+13+21 = 1+2+3+5+34 = 1+2+
8+34 = 3+8+34 (c=6)
46 = 1+3+8+13+21 = 1+3+8+34 (c=2)
47 = 2+3+8+13+21 = 5+8+13+21 = 2+3+8+34 = 5+8+34 = 13+34 (c=5)
48 = 1+2+3+8+13+21 = 1+5+8+13+21 = 1+2+3+8+34 = 1+5+8+34 = 1+13+
34 (c=5)
49 = 2+5+8+13+21 = 2+5+8+34 = 2+13+34 (c=3)
50 = 1+2+5+8+13+21 = 3+5+8+13+21 = 1+2+5+8+34 = 3+5+8+34 = 1+2+1
3+34 = 3+13+34 (c=6)
51 = 1+3+5+8+13+21 = 1+3+5+8+34 = 1+3+13+34 (c=3)
52 = 2+3+5+8+13+21 = 2+3+5+8+34 = 2+3+13+34 = 5+13+34 (c=4)
53 = 1+2+3+5+8+13+21 = 1+2+3+5+8+34 = 1+2+3+13+34 = 1+5+13+34 (c=4)
54 = 2+5+13+34 (c=1)
55 = 1+2+5+13+34 = 3+5+13+34 = 8+13+34 = 21+34 = 55 (c=5)
56 = 1+3+5+13+34 = 1+8+13+34 = 1+21+34 = 1+55 (c=4)

The patterns are easier to see when the counts are set out like this:

1, 1, 2, 1, 2, 2, 1, 3, 2, 2, 3, 1, 3, 3, 2, 4, 2, 3, 3, 1, 4, 3, 3, 5, 2, 4, 4, 2, 5, 3, 3, 4, 1, 4, 4, 3, 6, 3, 5, 5, 2, 6, 4, 4, 6, 2, 5, 5, 3, 6, 3, 4, 4, 1, 5, 4, 4, 7, 3, 6, 6, 3, 8, 5, 5, 7, 2, 6, 6, 4, 8, 4, 6, 6, 2, 7, 5, 5, 8, 3, 6, 6, 3, 7, 4, 4, 5, 1, 5, 5, 4, 8, 4, 7, 7, 3, 9, 6, 6, 9, 3, 8, 8, 5, 10, 5, 7, 7, 2, 8, 6, 6, 10, 4, 8, 8, 4, 10, 6, 6, 8, 2, 7, 7, 5, 10, 5, 8, 8, 3, 9, 6, 6, 9, 3, 7, 7, 4, 8, 4, 5, 5, 1, 6, 5, 5, 9, 4, 8, 8… 1… — See A000119, Number of representations of n as a sum of distinct Fibonacci numbers, at the Online Encyclopedia of Integer Sequences (OEIS)

The numbers between each pair of 1s are symmetrical:

1, 2, 1,
1, 2, 2, 1,
1, 3, 2, 2, 3, 1,
1, 3, 3, 2, 4, 2, 3, 3, 1
1, 4, 3, 3, 5, 2, 4, 4, 2, 5, 3, 3, 4, 1

And when fibsumcount(n) = 1, then n = fib(i)-1, i.e. n is one less than a Fibonacci number:

1 = 1 (c=1)
2 = 2 (c=1)
4 = 1+3 (c=1)
7 = 2+5 (c=1)
12 = 1+3+8 (c=1)
20 = 2+5+13 (c=1)
33 = 1+3+8+21 (c=1)
54 = 2+5+13+34 (c=1)
88 = 1+3+8+21+55 (c=1)
143 = 2+5+13+34+89 (c=1)
232 = 1+3+8+21+55+144 (c=1)
376 = 2+5+13+34+89+233 (c=1)
609 = 1+3+8+21+55+144+377 (c=1)
986 = 2+5+13+34+89+233+610 (c=1)
1596 = 1+3+8+21+55+144+377+987 (c=1)
2583 = 2+5+13+34+89+233+610+1597 (c=1)
4180 = 1+3+8+21+55+144+377+987+2584 (c=1)
6764 = 2+5+13+34+89+233+610+1597+4181 (c=1)
10945 = 1+3+8+21+55+144+377+987+2584+6765 (c=1)
17710 = 2+5+13+34+89+233+610+1597+4181+10946 (c=1)
[…]

I also noticed a pattern relating to the maximum count reached in the numbers between the 1s. Suppose the function max(fib(i)-1..fib(i+1)-1) returns the highest count of ways to represent the numbers from fib(i)-1 to fib(i+1)-1. Notice how max() increases:

max(2..4) = 2
max(4..7) = 2
max(7..12) = 3
max(12..20) = 4
max(20..33) = 5
max(33..54) = 6
max(54..88) = 8
max(88..143) = 10
max(143..232) = 13
max(232..376) = 16
max(376..609) = 21
max(609..986) = 26
max(986..1596) = 34
max(1596..2583) = 42
max(2583..4180) = 55
max(4180..6764) = 68
[…]

The pattern is described like this at the Online Encyclopedia of Integer Sequences:

a(n) = 1 if and only if n+1 is a Fibonacci number. The length of such a quasi-period (from Fib(i)-1 to Fib(i+1)-1, inclusive) is a Fibonacci number + 1. The maximum value of a(n) within each subsequent quasi-period increases by a Fibonacci number. For example, from n = 143 to n = 232, the maximum is 13. From 232 to 376, the maximum is 16, an increase of 3. From 376 to 609, 21, an increase of 5. From 609 to 986, 26, increasing by 5 again. Each two subsequent maxima seem to increase by the same increment, the next Fibonacci number. – Kerry Mitchell, Nov 14 2009

The maxima of the quasi-periods are in A096748. – Max Barrentine, Sep 13 2015 — See commentary for A000119 at OEIS

Here is A096748:

1, 2, 2, 2, 3, 4, 5, 6, 8, 10, 13, 16, 21, 26, 34, 42, 55, 68, 89, 110, 144, 178, 233, 288, 377, 466, 610, 754, 987, 1220, 1597, 1974, 2584, 3194, 4181, 5168, 6765, 8362, 10946, 13530, 17711, 21892, 28657, 35422, 46368, 57314, 75025, 92736, 121393, 150050 — A096748, Expansion of (1+x)^2/(1-x^2-x^4), at OEIS

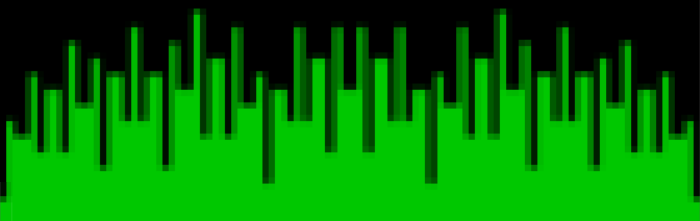
These maxima are the succesive highest points in a graph of A000119, Number of representations of n as a sum of distinct Fibonacci numbers:

Graph of count of ways in which 1,2,3… can be sum of distinct Fibonacci numbers

The graph looks like a furry caterpillar or similar and the symmetry of counts between the 1s is more obvious there:

fibsumcounts for 33..54

fibsumcounts for 54..88

fibsumcounts for 88..143

fibsumcounts for 143..232

fibsumcounts for 232..376

fibsumcounts for 376..609

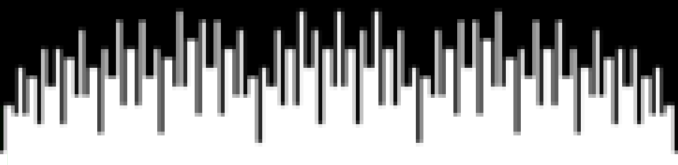
And the fractal nature of the counts is more obvious when the graph is rotated by 90° and then mirrored:

Rotated and mirrored graph of count of ways in which 1,2,3… can be sum of distinct Fibonacci numbers

The Fatal Factory

by in Arithmetic, Mathematics, Prime numbers, Puzzles, Squares and tagged , , , , , , , , , , , , , , , | Leave a comment

I can’t remember where I came across this clever little puzzle and what precise form it took, but here’s my version of it:

A famously eccentric inventor and recreational mathematician has invited you to tour the factory where his company manufactures locks, keys, safes, cash-boxes and so on. At the end of the tour he brings you to a conference room, pours you a glass of wine, and invites you to test your wits against a puzzle. He points out that a hundred numbered boxes have been set out on two long tables in the room. You sip your wine as you listen to him explain that each box is locked and contains a slip of paper bearing a number between 0 and 9. If you accept the challenge, the inventor will order a hundred workers to walk in turn past the boxes, using a master-key to unlock or lock the boxes like this:

The first worker will use the key on every box (boxes #1,2,3…), the second worker will use the key on every second box (boxes #2,4,6…), the third worker the key on every third box (boxes #3,6,9…), and so on.

Now, you can’t tell by simply looking at a box whether it’s unlocked or not, but it’s obvious that the first box will be unlocked when all that is over. Box #1 is originally locked and the master-key will be used on it just once. But how many other boxes will be unlocked? If you can choose nothing but the unlocked boxes, you get to keep the contents. Otherwise you get nothing. That is, if you choose one or more locked boxes, you get nothing.

And what good are the contents of the unlocked boxes? Well, if you take the numbered slips of paper they contain in order, they will give you the combination of a locked safe the inventor now points out in the wall behind you. The safe contains the antidote for the deadly but slow-acting poison he secretly slipped into the wine you have been sipping as you listened to him explain the details of the puzzle. So you have to choose all and only the unlocked boxes to save your life. Can you do it?

Solution

I’m sure there’s a simpler explanation of which boxes will be unlocked, but here’s my complicated one:

Whether box #n is locked or unlocked in the end depends on how many divisors the number n has. If it has an even number of divisors, it will be locked; if it has an odd number of divisors, it will be unlocked. Take box #12. The number 12 has six divisors: 1, 2, 3, 4, 6 and 12. So workers #1, #3 and #6 will unlock it with the master-key, but workers #2, #4 and #12 will lock it again. Worker #12 will be the final worker to use the master-key on the box, so it will be locked.

Now take box #16. The number #16 has five divisors: 1, 2, 4, 8 and 16. So workers #1, #4 and #16 will unlock the box with the master-key, while workers #2 and #8 will lock it. Worker #16 will be the final worker to use the master-key on the box, so it will be unlocked.

In other words, the puzzle reduces to this: Which numbers from 1 to 100 have an odd number of divisors? To work out the number of divisors n has, you add 1 to the exponent of each of its prime factors and multiply the results. For example, 24 has eight divisors thus:

• 24 = 2^3 * 3^1 → (3+1) * (1+1) = 4 * 2 = 8, so 24 has eight divisors: 1, 2, 3, 4, 6, 8, 12, 24

But 36 has nine divisors thus:

• 36 = 2^2 * 3^2 → (2+1) * (2+1) = 3 * 3 = 9, so 36 has nine divisors: 1, 2, 3, 4, 6, 9, 12, 18, 36

36 demonstrates that a number has to have only even exponents on its prime factors to have an odd number of divisors (the only number without prime factors is 1, which has one divisor, namely itself). Numbers with only even exponents on their prime factors are square numbers:

• 4 = 2^2 → (2+1) = 3, so 4 has three divisors: 1, 2, 4
• 9 = 3^2 → (2+1) = 3, so 9 has three divisors: 1, 3, 9
• 16 = 2^4 → (4+1) = 5, so 16 has five divisors: 1, 2, 4, 8, 16
• 25 = 5^2 → (2+1) = 3, so 25 has divisors: 1, 5, 25
• 36 = 2^2 * 3^2 → (2+1) * (2+1) = 3 * 3 = 9, so 36 has nine divisors: 1, 2, 3, 4, 6, 9, 12, 18, 36
• 49 = 7^2 → (2+1) = 3, so 49 has three divisors: 1, 7, 49
• 64 = 2^6 → (6+1) = 7, so 64 has seven divisors: 1, 2, 4, 8, 16, 32, 64
• 81 = 3^4 → (4+1) = 5, so 81 has five divisors: 1, 3, 9, 27, 81
• 100 = 2^2 * 5^2 → (2+1) * (2+1) = 3 * 3 = 9, so 100 has nine divisors: 1, 2, 4, 5, 10, 20, 25, 50, 100

So if you choose boxes #1, #4, #9, #16, #25, #36, #49, #64, #81 and #100, you’ll get the combination for the safe and save your life.

Appendix

Here’s the full description of what happens to the boxes:

• box #1 is unlocked by worker #1 and locked by no-one, therefore it’s unlocked
• box #2 is unlocked by worker #1 and locked by worker #2, therefore it’s locked
• box #3 is unlocked by worker #1 and locked by worker #3, therefore it’s locked
• box #4 is unlocked by workers #1 and #4, and locked by worker #2, therefore it’s unlocked
• box #5 is unlocked by worker #1 and locked by worker #5, therefore it’s locked
• box #6 is unlocked by workers #1 and #3, and locked by workers #2 and #6, therefore it’s locked
• box #7 is unlocked by worker #1 and locked by worker #7, therefore it’s locked
• box #8 is unlocked by workers #1 and #4, and locked by workers #2 and #8, therefore it’s locked
• box #9 is unlocked by workers #1 and #9, and locked by worker #3, therefore it’s unlocked
• box #10 is unlocked by workers #1 and #5, and locked by workers #2 and #10, therefore it’s locked
• box #11 is unlocked by worker #1 and locked by worker #11, therefore it’s locked
• box #12 is unlocked by workers #1, #3 and #6, and locked by workers #2, #4 and #12, therefore it’s locked
• box #13 is unlocked by worker #1 and locked by worker #13, therefore it’s locked
• box #14 is unlocked by workers #1 and #7, and locked by workers #2 and #14, therefore it’s locked
• box #15 is unlocked by workers #1 and #5, and locked by workers #3 and #15, therefore it’s locked
• box #16 is unlocked by workers #1, #4 and #16, and locked by workers #2 and #8, therefore it’s unlocked
• box #17 is unlocked by worker #1 and locked by worker #17, therefore it’s locked
• box #18 is unlocked by workers #1, #3 and #9, and locked by workers #2, #6 and #18, therefore it’s locked
• box #19 is unlocked by worker #1 and locked by worker #19, therefore it’s locked
• box #20 is unlocked by workers #1, #4 and #10, and locked by workers #2, #5 and #20, therefore it’s locked
• box #21 is unlocked by workers #1 and #7, and locked by workers #3 and #21, therefore it’s locked
• box #22 is unlocked by workers #1 and #11, and locked by workers #2 and #22, therefore it’s locked
• box #23 is unlocked by worker #1 and locked by worker #23, therefore it’s locked
• box #24 is unlocked by workers #1, #3, #6 and #12, and locked by workers #2, #4, #8 and #24, therefore it’s locked
• box #25 is unlocked by workers #1 and #25, and locked by worker #5, therefore it’s unlocked
• box #26 is unlocked by workers #1 and #13, and locked by workers #2 and #26, therefore it’s locked
• box #27 is unlocked by workers #1 and #9, and locked by workers #3 and #27, therefore it’s locked
• box #28 is unlocked by workers #1, #4 and #14, and locked by workers #2, #7 and #28, therefore it’s locked
• box #29 is unlocked by worker #1 and locked by worker #29, therefore it’s locked
• box #30 is unlocked by workers #1, #3, #6 and #15, and locked by workers #2, #5, #10 and #30, therefore it’s locked
• box #31 is unlocked by worker #1 and locked by worker #31, therefore it’s locked
• box #32 is unlocked by workers #1, #4 and #16, and locked by workers #2, #8 and #32, therefore it’s locked
• box #33 is unlocked by workers #1 and #11, and locked by workers #3 and #33, therefore it’s locked
• box #34 is unlocked by workers #1 and #17, and locked by workers #2 and #34, therefore it’s locked
• box #35 is unlocked by workers #1 and #7, and locked by workers #5 and #35, therefore it’s locked
• box #36 is unlocked by workers #1, #3, #6, #12 and #36, and locked by workers #2, #4, #9 and #18, therefore it’s unlocked
• box #37 is unlocked by worker #1 and locked by worker #37, therefore it’s locked
• box #38 is unlocked by workers #1 and #19, and locked by workers #2 and #38, therefore it’s locked
• box #39 is unlocked by workers #1 and #13, and locked by workers #3 and #39, therefore it’s locked
• box #40 is unlocked by workers #1, #4, #8 and #20, and locked by workers #2, #5, #10 and #40, therefore it’s locked
• box #41 is unlocked by worker #1 and locked by worker #41, therefore it’s locked
• box #42 is unlocked by workers #1, #3, #7 and #21, and locked by workers #2, #6, #14 and #42, therefore it’s locked
• box #43 is unlocked by worker #1 and locked by worker #43, therefore it’s locked
• box #44 is unlocked by workers #1, #4 and #22, and locked by workers #2, #11 and #44, therefore it’s locked
• box #45 is unlocked by workers #1, #5 and #15, and locked by workers #3, #9 and #45, therefore it’s locked
• box #46 is unlocked by workers #1 and #23, and locked by workers #2 and #46, therefore it’s locked
• box #47 is unlocked by worker #1 and locked by worker #47, therefore it’s locked
• box #48 is unlocked by workers #1, #3, #6, #12 and #24, and locked by workers #2, #4, #8, #16 and #48, therefore it’s locked
• box #49 is unlocked by workers #1 and #49, and locked by worker #7, therefore it’s unlocked
• box #50 is unlocked by workers #1, #5 and #25, and locked by workers #2, #10 and #50, therefore it’s locked
• box #51 is unlocked by workers #1 and #17, and locked by workers #3 and #51, therefore it’s locked
• box #52 is unlocked by workers #1, #4 and #26, and locked by workers #2, #13 and #52, therefore it’s locked
• box #53 is unlocked by worker #1 and locked by worker #53, therefore it’s locked
• box #54 is unlocked by workers #1, #3, #9 and #27, and locked by workers #2, #6, #18 and #54, therefore it’s locked
• box #55 is unlocked by workers #1 and #11, and locked by workers #5 and #55, therefore it’s locked
• box #56 is unlocked by workers #1, #4, #8 and #28, and locked by workers #2, #7, #14 and #56, therefore it’s locked
• box #57 is unlocked by workers #1 and #19, and locked by workers #3 and #57, therefore it’s locked
• box #58 is unlocked by workers #1 and #29, and locked by workers #2 and #58, therefore it’s locked
• box #59 is unlocked by worker #1 and locked by worker #59, therefore it’s locked
• box #60 is unlocked by workers #1, #3, #5, #10, #15 and #30, and locked by workers #2, #4, #6, #12, #20 and #60, therefore it’s locked
• box #61 is unlocked by worker #1 and locked by worker #61, therefore it’s locked
• box #62 is unlocked by workers #1 and #31, and locked by workers #2 and #62, therefore it’s locked
• box #63 is unlocked by workers #1, #7 and #21, and locked by workers #3, #9 and #63, therefore it’s locked
• box #64 is unlocked by workers #1, #4, #16 and #64, and locked by workers #2, #8 and #32, therefore it’s unlocked
• box #65 is unlocked by workers #1 and #13, and locked by workers #5 and #65, therefore it’s locked
• box #66 is unlocked by workers #1, #3, #11 and #33, and locked by workers #2, #6, #22 and #66, therefore it’s locked
• box #67 is unlocked by worker #1 and locked by worker #67, therefore it’s locked
• box #68 is unlocked by workers #1, #4 and #34, and locked by workers #2, #17 and #68, therefore it’s locked
• box #69 is unlocked by workers #1 and #23, and locked by workers #3 and #69, therefore it’s locked
• box #70 is unlocked by workers #1, #5, #10 and #35, and locked by workers #2, #7, #14 and #70, therefore it’s locked
• box #71 is unlocked by worker #1 and locked by worker #71, therefore it’s locked
• box #72 is unlocked by workers #1, #3, #6, #9, #18 and #36, and locked by workers #2, #4, #8, #12, #24 and #72, therefore it’s locked
• box #73 is unlocked by worker #1 and locked by worker #73, therefore it’s locked
• box #74 is unlocked by workers #1 and #37, and locked by workers #2 and #74, therefore it’s locked
• box #75 is unlocked by workers #1, #5 and #25, and locked by workers #3, #15 and #75, therefore it’s locked
• box #76 is unlocked by workers #1, #4 and #38, and locked by workers #2, #19 and #76, therefore it’s locked
• box #77 is unlocked by workers #1 and #11, and locked by workers #7 and #77, therefore it’s locked
• box #78 is unlocked by workers #1, #3, #13 and #39, and locked by workers #2, #6, #26 and #78, therefore it’s locked
• box #79 is unlocked by worker #1 and locked by worker #79, therefore it’s locked
• box #80 is unlocked by workers #1, #4, #8, #16 and #40, and locked by workers #2, #5, #10, #20 and #80, therefore it’s locked
• box #81 is unlocked by workers #1, #9 and #81, and locked by workers #3 and #27, therefore it’s unlocked
• box #82 is unlocked by workers #1 and #41, and locked by workers #2 and #82, therefore it’s locked
• box #83 is unlocked by worker #1 and locked by worker #83, therefore it’s locked
• box #84 is unlocked by workers #1, #3, #6, #12, #21 and #42, and locked by workers #2, #4, #7, #14, #28 and #84, therefore it’s locked
• box #85 is unlocked by workers #1 and #17, and locked by workers #5 and #85, therefore it’s locked
• box #86 is unlocked by workers #1 and #43, and locked by workers #2 and #86, therefore it’s locked
• box #87 is unlocked by workers #1 and #29, and locked by workers #3 and #87, therefore it’s locked
• box #88 is unlocked by workers #1, #4, #11 and #44, and locked by workers #2, #8, #22 and #88, therefore it’s locked
• box #89 is unlocked by worker #1 and locked by worker #89, therefore it’s locked
• box #90 is unlocked by workers #1, #3, #6, #10, #18 and #45, and locked by workers #2, #5, #9, #15, #30 and #90, therefore it’s locked
• box #91 is unlocked by workers #1 and #13, and locked by workers #7 and #91, therefore it’s locked
• box #92 is unlocked by workers #1, #4 and #46, and locked by workers #2, #23 and #92, therefore it’s locked
• box #93 is unlocked by workers #1 and #31, and locked by workers #3 and #93, therefore it’s locked
• box #94 is unlocked by workers #1 and #47, and locked by workers #2 and #94, therefore it’s locked
• box #95 is unlocked by workers #1 and #19, and locked by workers #5 and #95, therefore it’s locked
• box #96 is unlocked by workers #1, #3, #6, #12, #24 and #48, and locked by workers #2, #4, #8, #16, #32 and #96, therefore it’s locked
• box #97 is unlocked by worker #1 and locked by worker #97, therefore it’s locked
• box #98 is unlocked by workers #1, #7 and #49, and locked by workers #2, #14 and #98, therefore it’s locked
• box #99 is unlocked by workers #1, #9 and #33, and locked by workers #3, #11 and #99, therefore it’s locked
• box #100 is unlocked by workers #1, #4, #10, #25 and #100, and locked by workers #2, #5, #20 and #50, therefore it’s unlocked

Piles of Prime Pairs

by in Mathematics, Prime numbers and tagged , , , , | Leave a comment

A087641 Start of the first sequence of exactly n consecutive pairs of twin primes

29, 101, 5, 9419, 909287, 325267931, 678771479, 1107819732821, 170669145704411, 3324648277099157, 789795449254776509

Example: a(6)=325267931 is the starting point of the first occurrence of 6 consecutive pairs of twin primes: (325267931 325267933) (325267937 325267939) (325267949 325267951) (325267961 325267963) (325267979 325267981) (325267991 325267993).

• A087641 at the Encyclopedia of Integer Sequences

RubbuR

by in 2SLGBTQ+ Community Issues, Ancient Greek, Language and tagged , , , , , , , , , | Leave a comment

Etymology

From Middle French tribade, and its source, Latin tribad-, from Koine Greek τριβάς (tribás), from Ancient Greek τρίβω (tríbō, “to rub”).

磨鏡

Chinese: 磨 grindstone; to sharpen + to delay | 鏡 mirror; lens

trad. (磨鏡) 磨 鏡
simp. (磨镜) 磨 镜

Pronunciation

Mandarin

(Pinyin): mójìng
(Zhuyin): ㄇㄛˊ ㄐㄧㄥˋ

Southern Min (Hokkien, POJ): bôa-kiàⁿ

Middle Chinese: ma kjaengH

Old Chinese

(Baxter–Sagart): /*mˤaj C.qraŋʔ-s/
(Zhengzhang): /*maːl kraŋs/

Verb

磨鏡, to grind mirrors; 2. (now chiefly Xiamen Hokkien, euphemistic) to have lesbian sexual relations

• from tribade and 磨鏡 at Wiktionary

Abounding in Abundants

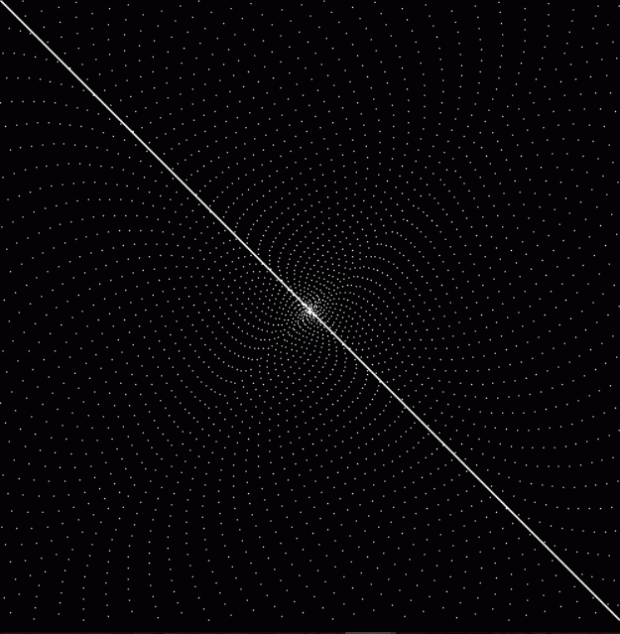
by in Arithmetic, Integer Sequences, Mathematics, Prime numbers and tagged , , , , , , , , , , , , , , , , | Leave a comment

This is the famous Ulam spiral, invented by the Jewish mathematician Stanisław Ulam (pronounced OO-lam) to represent prime numbers on a square grid:

The Ulam spiral of prime numbers

The red square represents 1, with 2 as the white block immediately to its right and 3 immediately above 2. Then 5 is the white block one space to the left of 3 and 7 the white block one space below 5. Then 11 is the white block right beside 2 and 13 the white block one space above 11. And so on. The primes aren’t regularly spaced on the spiral but patterns are nevertheless appearing. Here’s the Ulam spiral at higher resolutions:

The Ulam spiral x2

The Ulam spiral x4

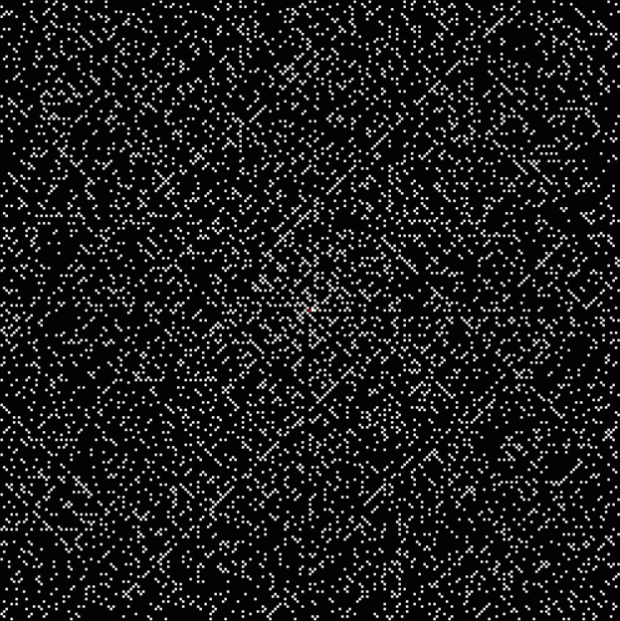
The primes are neither regular nor random in their distribution on the spiral. They stand tantalizingly betwixt and between. So the numbers represented on this Ulam-like spiral, which looks like an aerial view of a city designed by architects who occasionally get drunk:

Ulam-like spiral of abundant numbers

The distribution of abundant numbers is much more regular than the primes, but is far from wholly predictable. And what are abundant numbers? They’re numbers n such that sum(divisors(n)-n) > n. In other words, when you add the divisors of n less than n, the sum is greater than n. The first abundant number is 12:

12 is divisible by 1, 2, 3, 4, 6 → 1 + 2 + 3 + 4 + 6 = 16 > 12

The abundant numbers go like this:

12, 18, 20, 24, 30, 36, 40, 42, 48, 54, 56, 60, 66, 70, 72, 78, 80, 84, 88, 90, 96, 100, 102, 104, 108, 112, 114, 120, 126, 132, 138, 140, 144, 150, 156, 160, 162, 168, 174, 176, 180, 186, 192, 196, 198, 200, 204, 208, 210, 216, 220, 222, 224, 228, 234, 240, 246, 252, 258, 260, 264, 270… — A005101 at the Online Encyclopedia of Integer Sequences

Are all abundant numbers even? No, but the first odd abundant number takes a long time to arrive: it’s 45045. The abundance of 45045 was first discovered by the French mathematician Charles de Bovelles or Carolus Bovillus (c. 1475-1566), according to David Wells in his wonderful Penguin Dictionary of Curious and Interesting Numbers (1986):

45045 = 3^2 * 5 * 7 * 11 * 13 → 1 + 3 + 5 + 7 + 9 + 11 + 13 + 15 + 21 + 33 + 35 + 39 + 45 + 55 + 63 + 65 + 77 + 91 + 99 + 105 + 117 + 143 + 165 + 195 + 231 + 273 + 315 + 385 + 429 + 455 + 495 + 585 + 693 + 715 + 819 + 1001 + 1155 + 1287 + 1365 + 2145 + 3003 + 3465 + 4095 + 5005 + 6435 + 9009 + 15015 = 59787 > 45045

Here’s the spiral of abundant numbers at higher resolutions:

Abundant numbers x2

Abundant numbers x4

Negating the spiral of the abundant numbers — almost — is the spiral of the deficient numbers, where sum(divisors(n)-n) < n. Like most odd numbers, 15 is deficient:

15 = 3 * 5 → 1 + 3 + 5 = 9 < 15

Here’s the spiral of deficient numbers at various resolutions:

Deficient numbers on Ulam-like spiral

Deficient numbers x2

Deficient numbers x4

The spiral of deficient numbers doesn’t quite negate (reverse the colors of) the spiral of abundant numbers because of the very rare perfect numbers, where sum(divisors(n)-n) = n. That is, their factor-sums are exactly equal to themselves:

• 6 = 2 * 3 → 1 + 2 + 3 = 6
• 28 = 2^2 * 7 → 1 + 2 + 4 + 7 + 14 = 28
• 496 = 2^4 * 31 → 1 + 2 + 4 + 8 + 16 + 31 + 62 + 124 + 248 = 496

Now let’s try numbers n such than sum(divisors(n)) mod 2 = 1 (“n mod 2″ gives the remainder when n is divided by 2, i.e. n mod 2 is either 0 or 1). For example:

• 4 = 2^2 → 1 + 2 + 4 = 7 → 7 mod 2 = 1
• 18 = 2 * 3^2 → 1 + 2 + 3 + 6 + 9 + 18 = 39 → 39 mod 2 = 1
• 72 = 2^3 * 3^2 → 1 + 2 + 3 + 4 + 6 + 8 + 9 + 12 + 18 + 24 + 36 + 72 = 195 → 195 mod 2 = 1

Here are spirals for these numbers:

Ulam-like spiral for n such than sum(divisors(n)) mod 2 = 1

sum(divisors(n)) mod 2 = 1 x2

sum(divisors(n)) mod 2 = 1 x4

sum(divisors(n)) mod 2 = 1 x8

sum(divisors(n)) mod 2 = 1 x16