Category Archives: Fibonacci Sequence

Sequence Unfurls…

by in Arithmetic, Egyptian Fractions, Fibonacci Sequence, Integer Sequences, Mathematics and tagged , , , , | Leave a comment

The Fibonacci sequence is beautiful like clockwork. There’s a perfectly clear, rigorously defined mechanism ticking out an entirely predictable result for ever:

0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946, 17711, 28657, 46368, 75025, 121393, 196418, 317811, 514229, 832040, 1346269, 2178309, 3524578, 5702887, 9227465, 14930352, 24157817, 39088169, 63245986, 102334155, … — A000045 at the Online Encyclopedia of Integer Sequences (OEIS)

And there’s a formula to calculate any term in the sequence without calculating all the terms that precede it:

Binet’s formula for Fn, the n-th Fibonacci number

But I also like sequences that you might call definitely arbitrary. That is, there’s a perfectly clear, rigorously defined mechanism, but the results seem arbitrary — not predictable at all:

6, 15, 5, 22, 6, 3, 30, 9, 7, 2, 45, 15, 6, 5, 1, 36, 14, 6, 5, 3, 1, 62, 22, 16, 6, 5, 3, 2, 69, 21, 15, 4, 9, 5, 2, 1, 84, 30, 15, 9, 6, 7, 2, 2, 1, 56, 22, 13, 7, 3, 5, 2, 0, 0, 0, 142, 45, 22, 15, 12, 6, 9, 5, 3, 1, 2, 53, 17, 8, 4, 5, 1, 6, 3, 1, 1, 1, 0, 124, 36, 27, 14, 18, 6, 6, 5, 2, 3, 1, 1, 0, … A349083 at OEIS

What’s the formula there? That sequence is defined at the OEIS as “The number of three-term Egyptian fractions of rational numbers x/y, 0 < x/y < 1, ordered as below. The sequence is the number of (p,q,r) such that x/y = 1/p + 1/q + 1/r where p, q, and r are integers with p < q < r.” For example: “The sixth rational number is 3/4 [and] 3/4 = 1/2 + 1/5 + 1/20 = 1/2 + 1/6 + 1/12 = 1/3 + 1/4 + 1/5, so a(6)=3.”

Phascinating Phibonacci Phact Phor Phiday

by in Arithmetic, Fibonacci Sequence, Integer Sequences, φ, Mathematics, Phi and tagged , , , , , , , , | Leave a comment

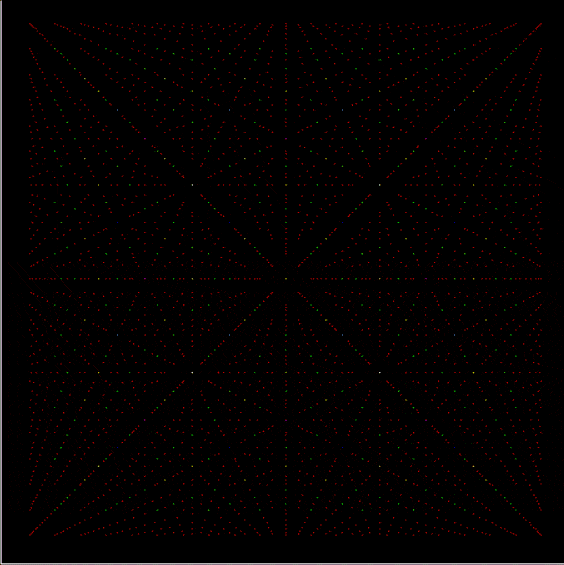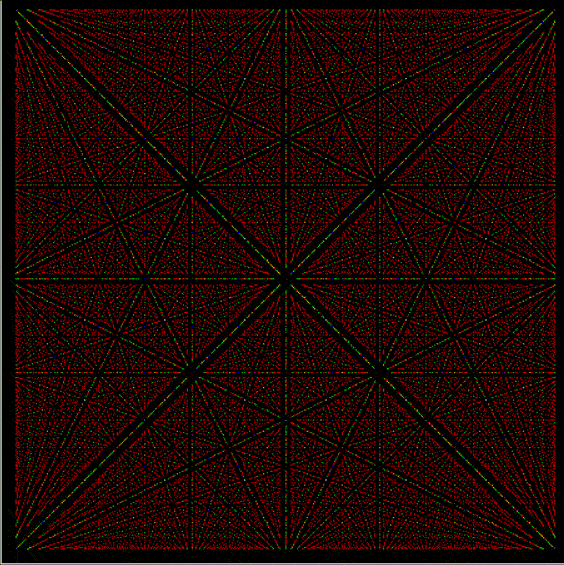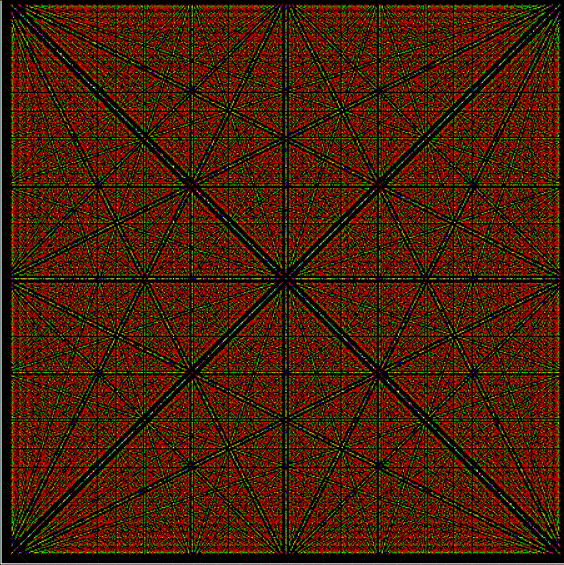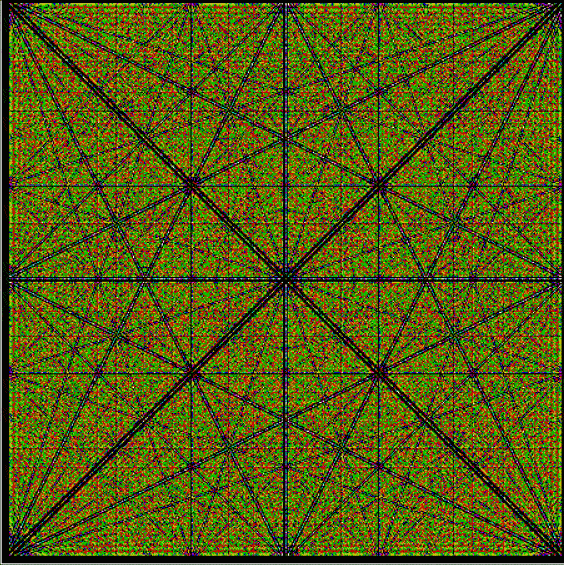
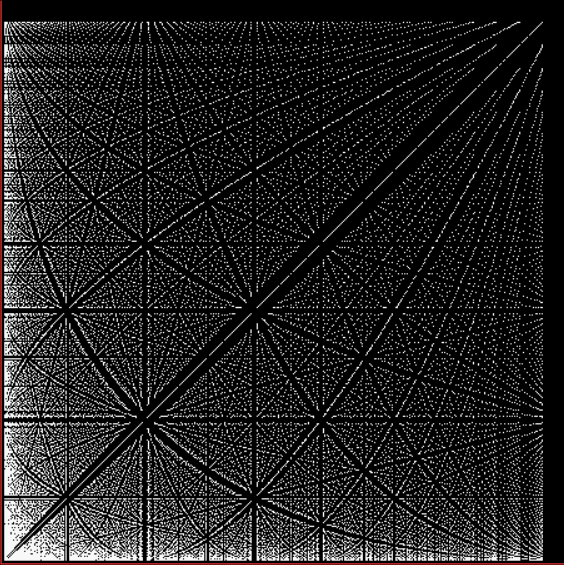
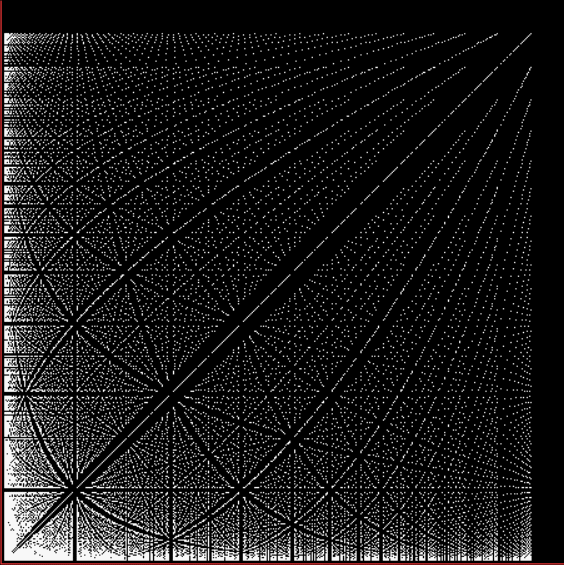
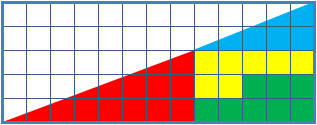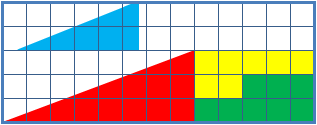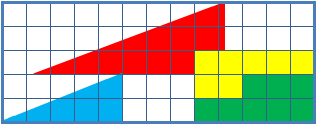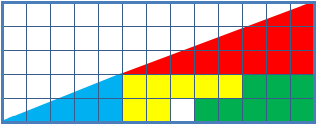
Phiday falls on the 11th, 12th and 23rd of each month, because 11, 12 and 23 represent entries in the famous Fibonacci sequence:

1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946, 17711, 28657, 46368, 75025, 121393, 196418, 317811, 514229, 832040, 1346269, 2178309, 3524578, 5702887, 9227465, 14930352, 24157817, 39088169, 63245986, 102334155, 165580141, 267914296, 433494437, 701408733, 1134903170, 1836311903, 2971215073, 4807526976, 7778742049, 12586269025, 20365011074, 32951280099, 53316291173, 86267571272, 139583862445, 225851433717, 365435296162, 591286729879, 956722026041, 1548008755920, 2504730781961, 4052739537881, 6557470319842, 10610209857723, 17167680177565, 27777890035288, 44945570212853, 72723460248141, 117669030460994, 190392490709135, 308061521170129, 498454011879264, 806515533049393, 1304969544928657, …

Successive entries in the Fibonacci sequence provide better and better approximations to the golden ratio or φ = 1.61803398874989484820458683…

2 = 2/1
1.5 = 3/2
1.6 = 5/3
1.6 = 8/5
1.625 = 13/8
1.6153846… = 21/13
1.619047619… = 34/21
1.6176470588235294117647… = 55/34
1.618… = 89/55
1.617977528… = 144/89
1.61805… = 233/144
1.618025751… = 377/233
1.618037135… = 610/377
1.618032786… = 987/610
1.618034447… = 1597/987
1.618033813… = 2584/1597
1.618034055… = 4181/2584
1.618033963… = 6765/4181
1.618033998… = 10946/6765
1.618033985… = 17711/10946

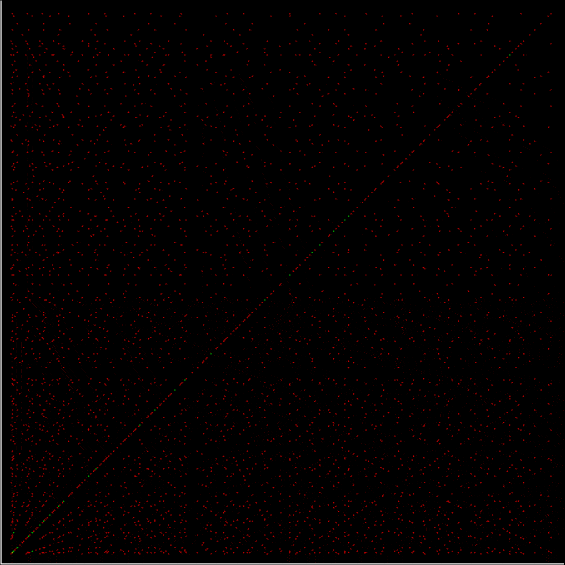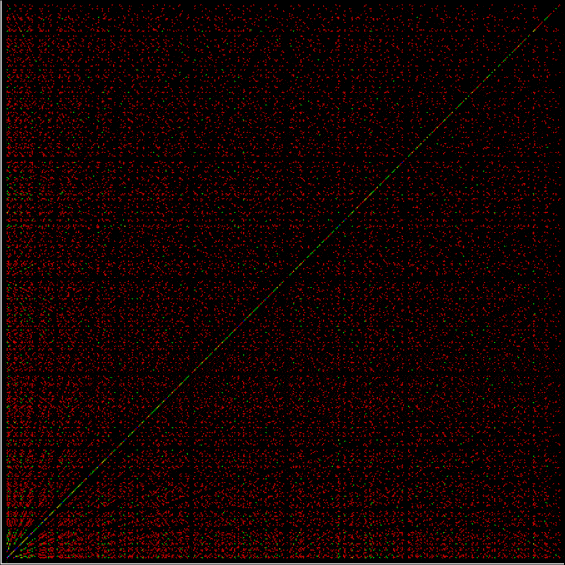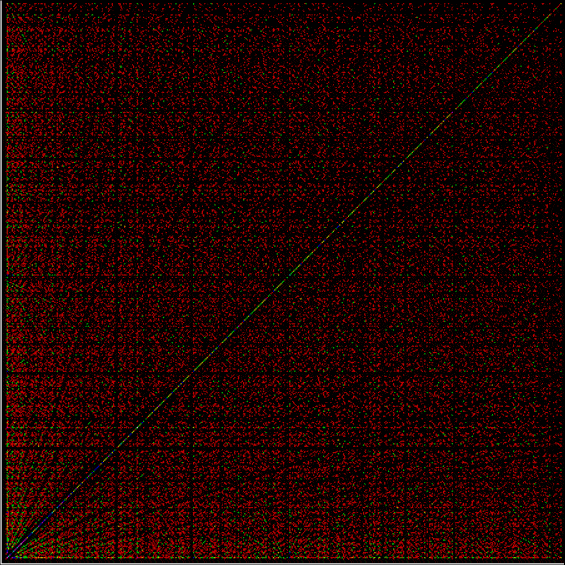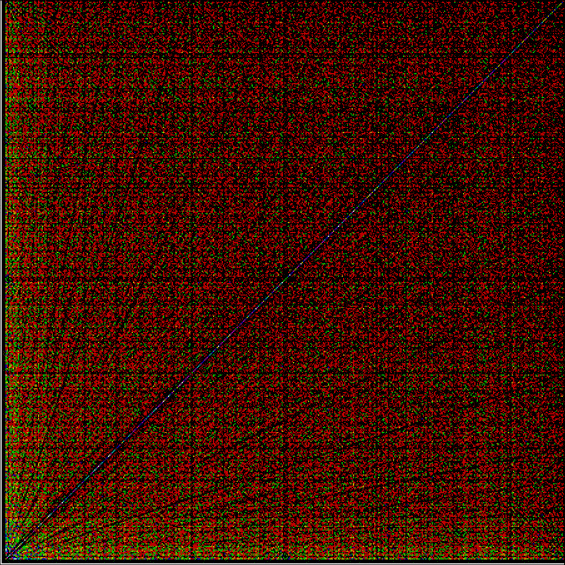
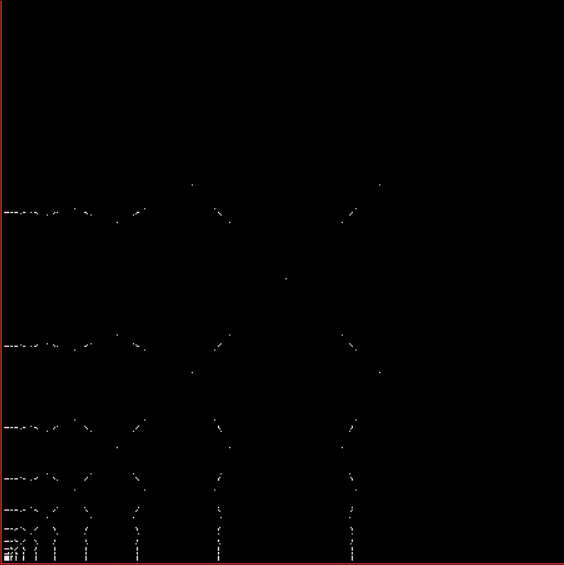
Today is 23rd June, so here’s a Fascinating Fibonacci Fact for Phiday. First, list the rational fractions < 1 in simplified form and mark the Fibonacci fractions:

1/2, 1/3, 2/3, 1/4, 3/4, 1/5, 2/5, 3/5, 4/5, 1/6, 5/6, 1/7, 2/7, 3/7, 4/7, 5/7, 6/7, 1/8, 3/8, 5/8, 7/8, 1/9, 2/9, 4/9, 5/9, 7/9, 8/9, 1/10, 3/10, 7/10, 9/10, 1/11, 2/11, 3/11, 4/11, 5/11, 6/11, 7/11, 8/11, 9/11, 10/11, 1/12, 5/12, 7/12, 11/12, 1/13, 2/13, 3/13, 4/13, 5/13, 6/13, 7/13, 8/13, 9/13, 10/13, 11/13, 12/13, 1/14, 3/14, 5/14, 9/14, 11/14, 13/14, 1/15, 2/15, 4/15, 7/15, 8/15, 11/15, 13/15, 14/15, 1/16, 3/16, 5/16, 7/16, 9/16, 11/16, 13/16, 15/16, 1/17, 2/17, 3/17, 4/17, 5/17, 6/17, 7/17, 8/17, 9/17, 10/17, 11/17, 12/17, 13/17, 14/17, 15/17, 16/17, 1/18, 5/18, 7/18, 11/18, 13/18, 17/18, 1/19, 2/19, 3/19, 4/19, 5/19, 6/19, 7/19, 8/19, 9/19, 10/19, 11/19, 12/19, 13/19, 14/19, 15/19, 16/19, 17/19, 18/19, 1/20, 3/20, 7/20, 9/20, 11/20, 13/20, 17/20, 19/20, 1/21, 2/21, 4/21, 5/21, 8/21, 10/21, 11/21, 13/21, 16/21, 17/21, 19/21, 20/21, 1/22, 3/22, 5/22, 7/22, 9/22, 13/22, 15/22, 17/22, 19/22, 21/22, 1/23, 2/23, 3/23, 4/23, 5/23, 6/23, 7/23, 8/23, 9/23, 10/23, 11/23, 12/23, 13/23, 14/23, 15/23, 16/23, 17/23, 18/23, 19/23, 20/23, 21/23, 22/23…

Next, record the positions in the fraction list of the FibFracs, i.e. pos(fibonacci(i)/fibonacci(i+1)) = pos(fibfrac(i)):

1, 3, 8, 20, 53, 135, 353, 924, 2422, 6311, 16529, 43229, 113066, 296173, 775286, 2029661, 5313844, 13911391, 36419909, 95348490, 249624578, 653521015, 1710943906, 4479312193, 11726939926, 30701521655, 80377560978, 210431191133, 550915866198, 1442316294349, 3776032465954, 9885782372588, 25881314454327, 67758160822605, 177393168080718, 464421339906882, 1215870841639593, …

What do you get when you divide pos(fibfrac(i+1)) by pos(fibfrac(i))?

pos(1/2) = 1
pos(2/3) = 3 (3/1 = 3)
pos(3/5) = 8 (8/3 = 2.6…)
pos(5/8) = 20 (20/8 = 2.5)
pos(8/13) = 53 (53/20 = 2.65)
pos(13/21) = 135 (2.5471698113207…)
pos(21/34) = 353 (2.6148…)
pos(34/55) = 924 (2.617563739376770538243626062…)
pos(55/89) = 2422 (2.621…)
pos(89/144) = 6311 (2.605697770437654830718414533…)
pos(144/233) = 16529 (2.619077800665504674378070037…)
pos(233/377) = 43229 (2.615342730957710690301893642…)
pos(377/610) = 113066 (2.615512734506928219482291980…)
pos(610/987) = 296173 (2.619470044045071020465922559…)
pos(987/1597) = 775286 (2.617679531895209894217231145…)
pos(1597/2584) = 2029661 (2.617951310871084993150914630…)
pos(2584/4181) = 5313844 (2.618094351716863062353762525…)
pos(4181/6765) = 13911391 (2.617952465296309037299551888…)
pos(6765/10946) = 36419909 (2.617991903182075753603647543…)
pos(10946/17711) = 95348490 (2.618032076906068051954770123…)
pos(17711/28657) = 249624578 (2.618023400265699016313735016…)
pos(28657/46368) = 653521015 (2.618015502463863954934758067…)
pos(46368/75025) = 1710943906 (2.618039614227248683043497844…)
pos(75025/121393) = 4479312193 (2.618035680358535377956453004…)
pos(121393/196418) = 11726939926 (2.618022459860278821159630657…)
pos(196418/317811) = 30701521655 (2.618033506501651708043379296…)
pos(317811/514229) = 80377560978 (2.618031831816708695313688353…)
pos(514229/832040) = 210431191133 (2.618034045479393794998913484…)
pos(832040/1346269) = 550915866198 (2.618033302153394031845776103…)
pos(1346269/2178309) = 1442316294349 (2.618033683260502304564996035…)
pos(2178309/3524578) = 3776032465954 (2.618033562227999267671331082…)
pos(3524578/5702887) = 9885782372588 (2.618034262608066669117450079…)
pos(5702887/9227465) = 25881314454327 (2.618034008728793003503058474…)
pos(9227465/14930352) = 67758160822605 (2.618033985181798482654668954…)
pos(14930352/24157817) = 177393168080718 (2.618033989221521810752093192…)
pos(24157817/39088169) = 464421339906882 (2.618033969017113072183685603…)
pos(39088169/63245986) = 1215870841639593 (2.618033964338027806153843993…)
[…]

In other words, pos(fibfrac(i+1)) / pos(fibfrac(i)) → φ^2 = 2.61803398874989484820458683… = φ + 1

Previously Pre-Posted (Please Peruse)

• Friday is Φiday

The Bellissima Curve

by in Arithmetic, Fibonacci Sequence, Geometry, Mathematics and tagged , , , , , , | Leave a comment

The bell curve is a shape that appears when you make a graph by counting all possible sums of a range of integers like 1, 2, 3, 4, 5, 6, 7, 8, 9, 10. The smallest sum you can get is 1; the largest is 55 = 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10. But there’s only one sum of 1 and only one sum of 55. Other sums are more common:

• 10 = 1 + 2 + 3 + 4
• 10 = 1 + 2 + 7
• 10 = 1 + 3 + 6
• 10 = 1 + 4 + 5
• 10 = 2 + 3 + 5
• 10 = 2 + 8
• 10 = 3 + 7
• 10 = 4 + 6
• 10 = 10

So there are nine sums of 10. If you graph count-sums with a bigger set of consecutive integers from 1, 2, 3…, you get this shape:

Bell curve from sum-counts with 1, 2, 3, 4, 5, 6, 7, 8, 9, 10…
(open in separate window for full-sized image)

It’s a bell curve. Et c’est une belle curve, a “beautiful curve” in French. But I’ve found what I call bellissime curve — Italian for “most beautiful curves” — by sampling different sets of integers. With the set (1, 3, 5, 7, 9, 11, 13, 15, 17, 19…), you get what you could call a slightly wrinkled bell curve:

Wrinkled bell-curve from sum-counts with 1, 3, 5, 7, 9, 11, 13, 15, 17, 19…
(open in separate window for full-sized image)

After that, as you leave bigger gaps in the sampled sets, the curves start to overlap and add extra beauty:

Overlapping bell curves from sum-counts with 1, 4, 7, 10, 13, 16, 19, 22, 25, 28…

Bellissima curves from sum-counts with 1, 5, 9, 13, 17, 21, 25, 29, 33, 37…

Bellissima curves from sum-counts with 1, 6, 11, 16, 21, 26, 31, 36, 41, 46…

Bellissima curves from sum-counts with 1, 7, 13, 19, 25, 31, 37, 43, 49, 55…

With the set (3, 6, 9, 15, 18, 21…), the bell is back:

Bell curve from sum-counts with 3, 6, 9, 15, 18, 21…

But with (4, 7, 10, 13, 6, 19…), separated by the same distance, you get this:

Bell curve from sum-counts with 4, 7, 10, 13, 6, 19…

When you sample the Fibonacci numbers, (1, 2, 3, 5, 8…), you get this graph:

Caterpillar curve from sum-counts of Fibonacci numbers 1, 2, 3, 5, 8, 13, 21, 34, 55, 89…

When you sample a restricted set of Fibonaccis, (1, 3, 8, 21, 55…), you get this, where each vertical line represents a count of one:

Golden gaps from sum-counts of restricted Fibonacci numbers 1, 3, 8, 21, 55, 144…

That restricted Fibonacci graph is strangely attractive, because it has golden gaps (verb sap!).

Friday is Φiday

by in Arithmetic, Fibonacci Sequence, Integer Sequences, φ, Mathematics, Phi and tagged , , , , , | Leave a comment

The 11th, 12th and 23rd day of a month can be called a φ-day (pronounced fy-day). Why so? Because those numbers are consecutive entries in the famous Fibonacci sequence, which offers better and better approximations to a mathematical constant called φ = (√5 + 1) / 2 = 1.6180339887498948…:

1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946, 17711, …

Each number after the second is the sum of the preceding two (so 11, 12, 23… could be the start of a similar sequence). When you divide fib(i) by fib(i-1), you get these approximations to φ:

2 = 2/1
1.5 = 3/2
1.6 = 5/3
1.6 = 8/5
1.625 = 13/8
1.6153846… = 21/13
1.619047619… = 34/21
1.6176470588235294117647… = 55/34
1.618… = 89/55
1.617977528… = 144/89
1.61805… = 233/144
1.618025751… = 377/233
1.618037135… = 610/377
1.618032786… = 987/610
1.618034447… = 1597/987
1.618033813… = 2584/1597
1.618034055… = 4181/2584
1.618033963… = 6765/4181
1.618033998… = 10946/6765
1.618033985… = 17711/10946

Today is the 23rd and not just a φ-day but a Friday (or φriday). So here’s one of the interesting results I’ve recently found while playing with the Fibonacci sequence. As any recreational mathematician kno, you can also find the Fibonacci sequence — and φ — with this little algorithm:

f = 0
LOOP
f = 1 / (f + 1)
print(f)
goto LOOP

The algorithm returns these values:

1, 1/2, 2/3, 3/5, 5/8, 8/13, 13/21, 21/34, 34/55, 55/89, 89/144, 144/233, 233/377, 377/610, 610/987, 987/1597, 1597/2584, 2584/4181, 4181/6765, 6765/10946, 10946/17711, …

I was playing with that algorithm and got an unexpected result with a simple adaptation of it:

f = 0
LOOP
f = 1 / (3 – f)
print(f)
goto LOOP

The values of f generated by this adapted algorithm are:

1/3, 3/8, 8/21, 21/55, 55/144, 144/377, 377/987, 987/2584, 2584/6765, 6765/17711, 17711/46368, 46368/121393, 121393/317811, 317811/832040, 832040/2178309, 2178309/5702887, 5702887/14930352, 14930352/39088169, 39088169/102334155, 102334155/267914296, …

The numerator and denominator in each fraction are next-but-one Fibonacci numbers, beautifully generated at each step:

3 – 0 = 3 → 1/3
3 – 1/3 = (3*3)/3 – 1/3 = 9/3 – 1/3 = (9-1) / 3 = 8 / 3 → 1/(8/3) = 3/8
3 – 3/8 = (3*8)/3 – 3/8 = 24/8 – 3/8 = (24-3) / 8 = 21/8 → 1/(21/8) = 8/21
3 – 8/21 = (3*21)/21 – 8/21 = 63/21 – 8/21 = (63-8)/21 = 55/21 → 1/(55/21) = 21/55
3 – 21/55 = (3*55)/55 – 21/55 = 165/55 – 21/55 = (165-21)/55 = 144/55 → 1/(144/55) = 55/144
3 – 55/144 = (3*144)/144 – 55/144 = (432-55)/144 = 377/144 → 1/(377/144) = 144/377
3 – 144/377 = (3*377)/377 – 144/377 = (1131-144)/377 = 987/377 → 1/(987/377) = 377/987
[…]

If you reverse numerator and denominator, the limit of the fraction is φ^2 = 2.6180339887498948… = φ+1:

3 = 3/1
2.6 = 8/3
2.625 = 21/8
2.6190476190476190476190476… = 55/21
2.6181818181818181818181818… = 144/55
2.6180555555555555555555555… = 377/144
2.6180371352785145888594164… = 987/377
2.6180344478216818642350557… = 2584/987
2.6180340557275541795665634… = 6765/2584
2.6180339985218033998521803… = 17711/6765
2.6180339901755970865563773… = 46368/17711
2.6180339889579020013802622… = 121393/46368
2.6180339887802426828565073… = 317811/121393
2.6180339887543225376088304… = 832040/317811
2.6180339887505408393827219… = 2178309/832040
2.6180339887499890970472967… = 5702887/2178309
2.6180339887499085989254214… = 14930352/5702887
2.6180339887498968544077192… = 39088169/14930352
2.6180339887498951409056791… = 102334155/39088169
2.6180339887498948909091006… = 267914296/102334155

The Call of CFulhu

by in Arithmetic, √2, Continued Fractions, Fibonacci Sequence, H.P. Lovecraft, Integer Sequences, φ, Mathematics, Phi, Square root of 2 and tagged , , , , , | Leave a comment

“The most merciful thing in the world, I think, is the inability of the human mind to correlate all its contents.” So said HPL in “The Call of Cthulhu” (1926). But I’d still like to correlate the contents of mine a bit better. For example, I knew that φ, the golden ratio, is the most irrational of all numbers, in that it is the slowest to be approximated with rational fractions. And I also knew that continued fractions, or CFs, were a way of representing both rationals and irrationals as a string of numbers, like this:

contfrac(10/7) = [1; 2, 3]
10/7 = 1 + 1/(2 + 1/3)
10/7 = 1.428571428571…

contfrac(3/5) = [0; 1, 1, 2]
4/5 = 0 + 1/(1 + 1/(1 + 1/2))
4/5 = 0.8

contfrac(11/8) = [1; 2, 1, 2]
11/8 = 1 + 1/(2 + 1/(1 + 1/2))
11/8 = 1.375

contfrac(4/7) = [0; 1, 1, 3]
4/7 = 0 + 1/(1 + 1/(1 + 1/3))
4/7 = 0.57142857142…

contfrac(17/19) = [0; 1, 8, 2]
17/19 = 0 + 1/(1 + 1/(8 + 1/2))
17/19 = 0.8947368421052…

contfrac(8/25) = [0; 3, 8]
8/25 = 0 + 1/(3 + 1/8)
8/25 = 0.32

contfrac(√2) = [1; 2, 2, 2, 2, 2, 2, 2…] = [1; 2]

√2 = 1 + 1/(2 + 1/(2 + 1/(2 + 1/(2 + 1/(2 + 1/(2 + 1/2 + …))))))

√2 = 1.41421356237309504…

contfrac(φ) = [1; 1, 1, 1, 1, 1, 1, 1, 1…]

φ = 1/(1 + 1/(1 + 1/(1 + 1/(1 + 1/(1 + 1/(1 + 1/(1 + 1/1 + …)))))))

φ = 1.6180339887498948…

But I didn’t correlate those two contents of my mind: the maximal irrationality of φ and the way continued fractions work.

That’s why I was surprised when I was looking at the continued fractions of 2..(n-1) / n for 3,4,5,6,7… That is, I was looking at the continued fractions of 2/3, 3/4, 2/5, 3/5, 4/5, 5/6, 2/7, 3/7… (skipping fractions like 2/4, 2/6, 3/6 etc, because they’re reducible: 2/4 = ½, 2/6 = 1/3, 3/6 = ½ etc). I wondered which fractions set successive records for the length of their continued fractions as one worked through ½, 2/3, 3/4, 2/5, 3/5, 4/5, 5/6, 2/7, 3/7… And because I hadn’t correlated the contents of my mind, I was surprised at the result. I shouldn’t have been, of course:

contfrac(1/2) = [0; 2] (cfl=1)
1/2 = 0 + 1/2
1/2 = 0.5

contfrac(2/3) = [0; 1, 2] (cfl=2)
2/3 = 0 + 1/(1 + 1/2)
2/3 = 0.666666666…

contfrac(3/5) = [0; 1, 1, 2] (cfl=3)
3/5 = 0 + 1/(1 + 1/(1 + 1/2))
3/5 = 0.6

contfrac(5/8) = [0; 1, 1, 1, 2] (cfl=4)
5/8 = 0 + 1/(1 + 1/(1 + 1/(1 + 1/2)))
5/8 = 0.625

contfrac(8/13) = [0; 1, 1, 1, 1, 2] (cfl=5)
8/13 = 0 + 1/(1 + 1/(1 + 1/(1 + 1/(1 + 1/2))))
8/13 = 0.615384615…

contfrac(13/21) = [0; 1, 1, 1, 1, 1, 2] (cfl=6)
13/21 = 0 + 1/(1 + 1/(1 + 1/(1 + 1/(1 + 1/(1 + 1/2)))))
13/21 = 0.619047619…

contfrac(21/34) = [0; 1, 1, 1, 1, 1, 1, 2] (cfl=7)
21/34 = 0 + 1/(1 + 1/(1 + 1/(1 + 1/(1 + 1/(1 + 1/(1 + 1/2))))))
21/34 = 0.617647059…

contfrac(34/55) = [0; 1, 1, 1, 1, 1, 1, 1, 2] (cfl=8)
contfrac(55/89) = [0; 1, 1, 1, 1, 1, 1, 1, 1, 2] (cfl=9)
contfrac(89/144) = [0; 1, 1, 1, 1, 1, 1, 1, 1, 1, 2] (cfl=10)
contfrac(144/233) = [0; 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 2] (cfl=11)
contfrac(233/377) = [0; 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 2] (cfl=12)
contfrac(377/610) = [0; 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 2] (cfl=13)
contfrac(610/987) = [0; 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 2] (cfl=14)
contfrac(987/1597) = [0; 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 2] (cfl=15)
contfrac(1597/2584) = [0; 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 2] (cfl=16)
contfrac(2584/4181) = [0; 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 2] (cfl=17)
contfrac(4181/6765) = [0; 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 2] (cfl=18)
[…]

Which n1/n2 set records for the length of their continued fractions (with n2 > n1)? It’s the successive Fibonacci fractions, fib(i)/fib(i+1), of course. I didn’t anticipate that answer because I didn’t understand φ and continued fractions properly. And I still don’t, because I’ve been surprised again today looking at palindromic CFs like these:

contfrac(2/5) = [0; 2, 2] (cfl=2)
2/5 = 0 + 1/(2 + 1/2)
2/5 = 0.4

contfrac(3/8) = [0; 2, 1, 2] (cfl=3)
3/8 = 0 + 1/(2 + 1/(1 + 1/2))
3/8 = 0.375

contfrac(3/10) = [0; 3, 3] (cfl=2)
3/10 = 0 + 1/(3 + 1/3)
3/10 = 0.3

contfrac(5/12) = [0; 2, 2, 2] (cfl=3)
5/12 = 0 + 1/(2 + 1/(2 + 1/2))
5/12 = 0.416666666…

contfrac(5/13) = [0; 2, 1, 1, 2] (cfl=4)
5/13 = 0 + 1/(2 + 1/(1 + 1/(1 + 1/2)))
5/13 = 0.384615384…

contfrac(4/15) = [0; 3, 1, 3] (cfl=3)
4/15 = 0 + 1/(3 + 1/(1 + 1/3))
4/15 = 0.266666666…

contfrac(7/16) = [0; 2, 3, 2] (cfl=3)
7/16 = 0 + 1/(2 + 1/(3 + 1/2))
7/16 = 0.4375

contfrac(4/17) = [0; 4, 4] (cfl=2)
4/17 = 0 + 1/(4 + 1/4)
4/17 = 0.235294117…

Again, I wondered which of these fractions set successive records for the length of their palindromic continued fractions. Here’s the answer:

contfrac(1/2) = [0; 2] (cfl=1)
1/2 = 0 + 1/2
1/2 = 0.5

contfrac(2/5) = [0; 2, 2] (cfl=2)
2/5 = 0 + 1/(2 + 1/2)
2/5 = 0.4

contfrac(3/8) = [0; 2, 1, 2] (cfl=3)
3/8 = 0 + 1/(2 + 1/(1 + 1/2))
3/8 = 0.375

contfrac(5/13) = [0; 2, 1, 1, 2] (cfl=4)
5/13 = 0 + 1/(2 + 1/(1 + 1/(1 + 1/2)))
5/13 = 0.384615384…

contfrac(8/21) = [0; 2, 1, 1, 1, 2] (cfl=5)
8/21 = 0 + 1/(2 + 1/(1 + 1/(1 + 1/(1 + 1/2))))
8/21 = 0.380952380…

contfrac(13/34) = [0; 2, 1, 1, 1, 1, 2] (cfl=6)
13/34 = 0 + 1/(2 + 1/(1 + 1/(1 + 1/(
1 + 1/(1 + 1/2)))))
13/34 = 0.382352941..

contfrac(21/55) = [0; 2, 1, 1, 1, 1, 1, 2] (cfl=7)
21/55 = 0 + 1/(2 + 1/(1 + 1/(1 + 1/(1 + 1/(1 + 1/(1 + 1/2))))))
21/55 = 0.381818181…

contfrac(34/89) = [0; 2, 1, 1, 1, 1, 1, 1, 2] (cfl=8)
contfrac(55/144) = [0; 2, 1, 1, 1, 1, 1, 1, 1, 2] (cfl=9)
contfrac(89/233) = [0; 2, 1, 1, 1, 1, 1, 1, 1, 1, 2] (cfl=10)
contfrac(144/377) = [0; 2, 1, 1, 1, 1, 1, 1, 1, 1, 1, 2] (cfl=11)
contfrac(233/610) = [0; 2, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 2] (cfl=12)
contfrac(377/987) = [0; 2, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 2] (cfl=13)
contfrac(610/1597) = [0; 2, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 2] (cfl=14)
contfrac(987/2584) = [0; 2, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 2] (cfl=15)
contfrac(1597/4181) = [0; 2, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 2] (cfl=16)
contfrac(2584/6765) = [0; 2, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 2] (cfl=17)
[…]

Now it’s the successive Fibonacci skip-one fractions, fib(i)/fib(i+2), that set records for the length of their palindromic continued fractions. But I think you’d have to be very good at maths not to be surprised by that result.

After that, I continued to be compelled by the Call of CFulhu and started to look at the CFs of Fibonacci skip-n fractions in general. That’s contfrac(fib(i)/fib(i+n)) for n = 1,2,3,… And I’ve found more interesting patterns, as I’ll describe in a follow-up post.

Fract-L Geometry

by in Arithmetic, Fibonacci Sequence, Geometry, Mathematics, Triangular Numbers and tagged , , , , , , , | Leave a comment

Suppose you set up an L, i.e. a vertical and horizontal line, representing the x,y coordinates between 0 and 1. Next, find the fractional pairs x = 1/2, 1/3, 2/3, 1/4, 2/4…, y = 1/2, 1/3, 2/3, 1/4, 2/4… and mark the point (x,y). That is, find the point, say, 1/5 of the way along the x-line, then the points 1/5, 2/5, 3/5 and 4/5 along the y-line, marking the points (1/5, 1/5), (1/5, 2/5), (1/5, 3/5), (1/5, 4/5). Then find (2/5, 1/5), (2/5, 2/5), (2/5, 3/5), (2/5, 4/5) and so on. Some interesting patterns appear in what I call a Frac-L (pronounced “frackle”) or Fract-L:

Frac-L for 1/2 to 21/22

Frac-L for 1/2 to 48/49

Frac-L for 1/2 to 75/76

Frac-L for 1/2 to 102/103

Frac-L for 1/2 to 102/103 (animated)

If the (x,y) point is first red, then becomes different colors as it is repeatedly found, you get these patterns:

Frac-L for 1/2 to 48/49 (color)

Frac-L for 1/2 to 75/79 (color)

Frac-L for 1/2 to 102/103 (color) (animated)

Now try polygonal numbers. The triangular numbers are 1, 3, 6, 10, 15, 21, 28, 36, 45, 55, 66, 78…, so you’re finding the fractional pairs, say, (1/21, 1/21), (1/21, 3/21, (1/21, 6/21), (1/21, 10/21), (1/21, 15/21), then (3/21, 1/21), (3/21, 3/21, (3/21, 6/21), (3/21, 10/21), (3/21, 15/21), and so on:

Frac-L for triangular fractions

The frac-L for square numbers (1, 4, 9, 16, 25, 36, 49, 64, 81, 100…) is almost identical:

Frac-L for square fractions, e.g. (1/16, 1/16), (1/16, 4/16), (1/16, 9/16)…

So is the frac-L for pentagonal numbers (1, 5, 12, 22, 35, 51, 70, 92, 117, 145, 176, 210, 247, 287, 330…):

Frac-L for pentagonal fractions, e.g. (1/35, 5/35), (1/35, 12/35), (1/35,22/35)…

Here are frac-Ls for tetrahedral and square-pyramidal numbers:

Frac-L for tetrahedral fractions

Frac-L for square pyramidal fractions

But what about prime numbers (skipping 2)? Here the fractional pairs are, say, (1/17, 1/17), (1/17, 3/17), (1/17, 5/17), (1/17, 7/17), (1/17, 11/17), (1/17, 13/17), then (3/17, 1/17), (3/17, 3/17), (3/17, 5/17), (3/17, 7/17), (3/17, 11/17), (3/17, 13/17), and so on:

Frac-L for 1/3 to 73/79 (prime fractions)

Frac-L for 1/3 to 223/227

Frac-L for 1/3 to 307/331

Frac-L for 1/3 to 307/331 (animated)

Frac-L for 1/3 to 73/79 (color) (prime fractions)

Frac-L for 1/3 to 223/227 (color)

Frac-L for 1/3 to 307/331 (color)

Frac-L for 1/3 to 307/331 (color) (animated)

And finally (for now), a frac-L for Fibonnaci numbers, where the fractional pairs are, say, (1/13, /13), (1/13, 2/13), (1/13, 3/13), (1/13, 5/13), (1/13, 8/13), then (2/13, /13), (2/13, 2/13), (2/13, 3/13), (2/13, 5/13), (2/13, 8/13), and so on:

Frac-L for Fibonacci fractions to 14930352/2178309 = fibonacci(36)/fibonacci(37)

Fabulous Furry Fibonacci Fractal

by in Arithmetic, Fibonacci Sequence, Fractals, Integer Sequences, Mathematics and tagged , , , , , , , , | Leave a comment

At least, I think it’s a fractal. I came across it when I was counting the ways in which the integers can be the sum of distinct Fibonacci numbers. Here for reference is the Fibonacci sequence, the beautiful and endlessly fertile sequence that’s seeded with “1, 1” and continued by summing the two previous numbers:

1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946, 17711, 28657, 46368, 75025, 121393, 196418, 317811, 514229, 832040…

I noticed some interesting patterns in the distinct-fib-num-sum count for the integers:

1 = 1 (count=1)
2 = 2 (count=1)
3 = 1+2 = 3 (count=2)
4 = 1+3 (c=1)
5 = 2+3 = 5 (c=2)
6 = 1+2+3 = 1+5 (c=2)
7 = 2+5 (c=1)
8 = 1+2+5 = 3+5 = 8 (c=3)
9 = 1+3+5 = 1+8 (c=2)
10 = 2+3+5 = 2+8 (c=2)
11 = 1+2+3+5 = 1+2+8 = 3+8 (c=3)
12 = 1+3+8 (c=1)
13 = 2+3+8 = 5+8 = 13 (c=3)
14 = 1+2+3+8 = 1+5+8 = 1+13 (c=3)
15 = 2+5+8 = 2+13 (c=2)
16 = 1+2+5+8 = 3+5+8 = 1+2+13 = 3+13 (c=4)
17 = 1+3+5+8 = 1+3+13 (c=2)
18 = 2+3+5+8 = 2+3+13 = 5+13 (c=3)
19 = 1+2+3+5+8 = 1+2+3+13 = 1+5+13 (c=3)
20 = 2+5+13 (c=1)
21 = 1+2+5+13 = 3+5+13 = 8+13 = 21 (c=4)
22 = 1+3+5+13 = 1+8+13 = 1+21 (c=3)
23 = 2+3+5+13 = 2+8+13 = 2+21 (c=3)
24 = 1+2+3+5+13 = 1+2+8+13 = 3+8+13 = 1+2+21 = 3+21 (c=5)
25 = 1+3+8+13 = 1+3+21 (c=2)
26 = 2+3+8+13 = 5+8+13 = 2+3+21 = 5+21 (c=4)
27 = 1+2+3+8+13 = 1+5+8+13 = 1+2+3+21 = 1+5+21 (c=4)
28 = 2+5+8+13 = 2+5+21 (c=2)
29 = 1+2+5+8+13 = 3+5+8+13 = 1+2+5+21 = 3+5+21 = 8+21 (c=5)
30 = 1+3+5+8+13 = 1+3+5+21 = 1+8+21 (c=3)
31 = 2+3+5+8+13 = 2+3+5+21 = 2+8+21 (c=3)
32 = 1+2+3+5+8+13 = 1+2+3+5+21 = 1+2+8+21 = 3+8+21 (c=4)
33 = 1+3+8+21 (c=1)
34 = 2+3+8+21 = 5+8+21 = 13+21 = 34 (c=4)
35 = 1+2+3+8+21 = 1+5+8+21 = 1+13+21 = 1+34 (c=4)
36 = 2+5+8+21 = 2+13+21 = 2+34 (c=3)
37 = 1+2+5+8+21 = 3+5+8+21 = 1+2+13+21 = 3+13+21 = 1+2+34 = 3+34
(c=6)
38 = 1+3+5+8+21 = 1+3+13+21 = 1+3+34 (c=3)
39 = 2+3+5+8+21 = 2+3+13+21 = 5+13+21 = 2+3+34 = 5+34 (c=5)
40 = 1+2+3+5+8+21 = 1+2+3+13+21 = 1+5+13+21 = 1+2+3+34 = 1+5+34
(c=5)
41 = 2+5+13+21 = 2+5+34 (c=2)
42 = 1+2+5+13+21 = 3+5+13+21 = 8+13+21 = 1+2+5+34 = 3+5+34 = 8+3
4 (c=6)
43 = 1+3+5+13+21 = 1+8+13+21 = 1+3+5+34 = 1+8+34 (c=4)
44 = 2+3+5+13+21 = 2+8+13+21 = 2+3+5+34 = 2+8+34 (c=4)
45 = 1+2+3+5+13+21 = 1+2+8+13+21 = 3+8+13+21 = 1+2+3+5+34 = 1+2+
8+34 = 3+8+34 (c=6)
46 = 1+3+8+13+21 = 1+3+8+34 (c=2)
47 = 2+3+8+13+21 = 5+8+13+21 = 2+3+8+34 = 5+8+34 = 13+34 (c=5)
48 = 1+2+3+8+13+21 = 1+5+8+13+21 = 1+2+3+8+34 = 1+5+8+34 = 1+13+
34 (c=5)
49 = 2+5+8+13+21 = 2+5+8+34 = 2+13+34 (c=3)
50 = 1+2+5+8+13+21 = 3+5+8+13+21 = 1+2+5+8+34 = 3+5+8+34 = 1+2+1
3+34 = 3+13+34 (c=6)
51 = 1+3+5+8+13+21 = 1+3+5+8+34 = 1+3+13+34 (c=3)
52 = 2+3+5+8+13+21 = 2+3+5+8+34 = 2+3+13+34 = 5+13+34 (c=4)
53 = 1+2+3+5+8+13+21 = 1+2+3+5+8+34 = 1+2+3+13+34 = 1+5+13+34 (c=4)
54 = 2+5+13+34 (c=1)
55 = 1+2+5+13+34 = 3+5+13+34 = 8+13+34 = 21+34 = 55 (c=5)
56 = 1+3+5+13+34 = 1+8+13+34 = 1+21+34 = 1+55 (c=4)

The patterns are easier to see when the counts are set out like this:

1, 1, 2, 1, 2, 2, 1, 3, 2, 2, 3, 1, 3, 3, 2, 4, 2, 3, 3, 1, 4, 3, 3, 5, 2, 4, 4, 2, 5, 3, 3, 4, 1, 4, 4, 3, 6, 3, 5, 5, 2, 6, 4, 4, 6, 2, 5, 5, 3, 6, 3, 4, 4, 1, 5, 4, 4, 7, 3, 6, 6, 3, 8, 5, 5, 7, 2, 6, 6, 4, 8, 4, 6, 6, 2, 7, 5, 5, 8, 3, 6, 6, 3, 7, 4, 4, 5, 1, 5, 5, 4, 8, 4, 7, 7, 3, 9, 6, 6, 9, 3, 8, 8, 5, 10, 5, 7, 7, 2, 8, 6, 6, 10, 4, 8, 8, 4, 10, 6, 6, 8, 2, 7, 7, 5, 10, 5, 8, 8, 3, 9, 6, 6, 9, 3, 7, 7, 4, 8, 4, 5, 5, 1, 6, 5, 5, 9, 4, 8, 8… 1… — See A000119, Number of representations of n as a sum of distinct Fibonacci numbers, at the Online Encyclopedia of Integer Sequences (OEIS)

The numbers between each pair of 1s are symmetrical:

1, 2, 1,
1, 2, 2, 1,
1, 3, 2, 2, 3, 1,
1, 3, 3, 2, 4, 2, 3, 3, 1
1, 4, 3, 3, 5, 2, 4, 4, 2, 5, 3, 3, 4, 1

And when fibsumcount(n) = 1, then n = fib(i)-1, i.e. n is one less than a Fibonacci number:

1 = 1 (c=1)
2 = 2 (c=1)
4 = 1+3 (c=1)
7 = 2+5 (c=1)
12 = 1+3+8 (c=1)
20 = 2+5+13 (c=1)
33 = 1+3+8+21 (c=1)
54 = 2+5+13+34 (c=1)
88 = 1+3+8+21+55 (c=1)
143 = 2+5+13+34+89 (c=1)
232 = 1+3+8+21+55+144 (c=1)
376 = 2+5+13+34+89+233 (c=1)
609 = 1+3+8+21+55+144+377 (c=1)
986 = 2+5+13+34+89+233+610 (c=1)
1596 = 1+3+8+21+55+144+377+987 (c=1)
2583 = 2+5+13+34+89+233+610+1597 (c=1)
4180 = 1+3+8+21+55+144+377+987+2584 (c=1)
6764 = 2+5+13+34+89+233+610+1597+4181 (c=1)
10945 = 1+3+8+21+55+144+377+987+2584+6765 (c=1)
17710 = 2+5+13+34+89+233+610+1597+4181+10946 (c=1)
[…]

I also noticed a pattern relating to the maximum count reached in the numbers between the 1s. Suppose the function max(fib(i)-1..fib(i+1)-1) returns the highest count of ways to represent the numbers from fib(i)-1 to fib(i+1)-1. Notice how max() increases:

max(2..4) = 2
max(4..7) = 2
max(7..12) = 3
max(12..20) = 4
max(20..33) = 5
max(33..54) = 6
max(54..88) = 8
max(88..143) = 10
max(143..232) = 13
max(232..376) = 16
max(376..609) = 21
max(609..986) = 26
max(986..1596) = 34
max(1596..2583) = 42
max(2583..4180) = 55
max(4180..6764) = 68
[…]

The pattern is described like this at the Online Encyclopedia of Integer Sequences:

a(n) = 1 if and only if n+1 is a Fibonacci number. The length of such a quasi-period (from Fib(i)-1 to Fib(i+1)-1, inclusive) is a Fibonacci number + 1. The maximum value of a(n) within each subsequent quasi-period increases by a Fibonacci number. For example, from n = 143 to n = 232, the maximum is 13. From 232 to 376, the maximum is 16, an increase of 3. From 376 to 609, 21, an increase of 5. From 609 to 986, 26, increasing by 5 again. Each two subsequent maxima seem to increase by the same increment, the next Fibonacci number. – Kerry Mitchell, Nov 14 2009

The maxima of the quasi-periods are in A096748. – Max Barrentine, Sep 13 2015 — See commentary for A000119 at OEIS

Here is A096748:

1, 2, 2, 2, 3, 4, 5, 6, 8, 10, 13, 16, 21, 26, 34, 42, 55, 68, 89, 110, 144, 178, 233, 288, 377, 466, 610, 754, 987, 1220, 1597, 1974, 2584, 3194, 4181, 5168, 6765, 8362, 10946, 13530, 17711, 21892, 28657, 35422, 46368, 57314, 75025, 92736, 121393, 150050 — A096748, Expansion of (1+x)^2/(1-x^2-x^4), at OEIS

These maxima are the succesive highest points in a graph of A000119, Number of representations of n as a sum of distinct Fibonacci numbers:

Graph of count of ways in which 1,2,3… can be sum of distinct Fibonacci numbers

The graph looks like a furry caterpillar or similar and the symmetry of counts between the 1s is more obvious there:

fibsumcounts for 33..54

fibsumcounts for 54..88

fibsumcounts for 88..143

fibsumcounts for 143..232

fibsumcounts for 232..376

fibsumcounts for 376..609

And the fractal nature of the counts is more obvious when the graph is rotated by 90° and then mirrored:

Rotated and mirrored graph of count of ways in which 1,2,3… can be sum of distinct Fibonacci numbers

Fib and Let Eye

by in Entomology, Fibonacci Sequence, Flowers, Mathematics, Natural History and tagged , , , , , , , , | Leave a comment

An ox-eye daisy (Leucanthemum sp.) with a harlequin ladybird, Harmonia axyridis, sitting at its center

Peri-Performative Post-Scriptum…

The title of this incendiary intervention refers to

1) The Fibonacci sequence present in the beautiful interlocking curves at the heart of the

2) daisy, whose name comes from Anglo-Saxon dæges ēage, meaning “day’s eye”.

3) The eye-like appearance of the daisy, with the ladybird like a slightly off-centered pupil

Bi-Bell Basics

by in Arithmetic, Base Behavior, Binary numbers, Blancmange Curves, Fibonacci Sequence, Fractals, Geometry, Mathematics, Powers and tagged , , , , , , , , , , , , , , , , , | Leave a comment

Here’s what you might call a Sisyphean sequence. It struggles upward, then slips back, over and over again:

1, 1, 2, 1, 2, 2, 3, 1, 2, 2, 3, 2, 3, 3, 4, 1, 2, 2, 3, 2, 3, 3, 4, 2, 3, 3, 4, 3, 4, 4, 5, 1, 2, 2, 3, 2, 3, 3, 4, 2, 3, 3, 4, 3, 4, 4, 5, 2, 3, 3, 4, 3, 4, 4, 5, 3, 4, 4, 5, 4, 5, 5, 6, 1, 2, 2, 3, 2, 3, 3, 4, 2, 3, 3, 4, 3, 4, 4, 5, 2, 3, 3, 4, 3, 4, 4, 5, 3, 4, 4, 5, 4, 5, 5, 6, 2, 3, 3, 4, 3, 4, 4, 5, 3, 4, 4, 5, 4, 5, 5, 6, 3, 4, 4, 5, 4, 5, 5, 6, 4, 5, 5, 6, 5, 6, 6, 7, 1, 2, 2, 3, 2, 3, 3, 4, 2...


The struggle goes on for ever. Every time it reaches a new maximum, it will fall back to 1 at the next step. And in fact 1, 2, 3 and all other integers occur infinitely often in the sequence, because it represents the digit-sums of binary numbers:

1 ← 1
1 = 1+0 ← 10 in binary = 2 in base ten
2 = 1+1 ← 11 = 3
1 = 1+0+0 ← 100 = 4
2 = 1+0+1 ← 101 = 5
2 = 1+1+0 ← 110 = 6
3 = 1+1+1 ← 111 = 7
1 = 1+0+0+0 ← 1000 = 8
2 = 1+0+0+1 ← 1001 = 9
2 = 1+0+1+0 ← 1010 = 10
3 = 1+0+1+1 ← 1011 = 11
2 = 1+1+0+0 ← 1100 = 12
3 = 1+1+0+1 ← 1101 = 13
3 = 1+1+1+0 ← 1110 = 14
4 = 1+1+1+1 ← 1111 = 15
1 = 1+0+0+0+0 ← 10000 = 16
2 = 1+0+0+0+1 ← 10001 = 17
2 = 1+0+0+1+0 ← 10010 = 18
3 = 1+0+0+1+1 ← 10011 = 19
2 = 1+0+1+0+0 ← 10100 = 20


Now here’s a related sequence in which all integers do not occur infinitely often:

1, 2, 3, 3, 4, 5, 6, 4, 5, 6, 7, 7, 8, 9, 10, 5, 6, 7, 8, 8, 9, 10, 11, 9, 10, 11, 12, 12, 13, 14, 15, 6, 7, 8, 9, 9, 10, 11, 12, 10, 11, 12, 13, 13, 14, 15, 16, 11, 12, 13, 14, 14, 15, 16, 17, 15, 16, 17, 18, 18, 19, 20, 21, 7, 8, 9, 10, 10, 11, 12, 13, 11, 12, 13, 14, 14, 15, 16, 17, 12, 13, 14, 15, 15, 16, 17, 18, 16, 17, 18, 19, 19, 20, 21, 22, 13, 14, 15, 16, 16, 17, 18, 19, 17, 18, 19, 20, 20, 21, 22, 23, 18, 19, 20, 21, 21, 22, 23, 24, 22, 23, 24, 25, 25, 26, 27, 28, 8, 9, 10, 11, 11, 12, 13, 14, 12, 13, 14, 15, 15...


The sequence represents the sum of the values of occupied columns in the binary numbers, reading from right to left:

10 in binary = 2 in base ten
21 (column values from right to left)
2*1 + 1*0 = 2

11 = 3
21
2*1 + 1*1 = 3

100 = 4
321 (column values from right to left)
3*1 + 2*0 + 1*0 = 3

101 = 5
321
3*1 + 2*0 + 1*1 = 4

110 = 6
321
3*1 + 2*1 + 1*0 = 5

111 = 7
321
3*1 + 2*1 + 1*1 = 6

1000 = 8
4321
4*1 + 3*0 + 2*0 + 1*0 = 4

1001 = 9
4321
4*1 + 3*0 + 2*0 + 1*1 = 5

1010 = 10
4321
4*1 + 3*0 + 2*1 + 1*0 = 6

1011 = 11
4321
4*1 + 3*0 + 2*1 + 1*1 = 7

1100 = 12
4321
4*1 + 3*1 + 2*0 + 1*0 = 7

1101 = 13
4321
4*1 + 3*1 + 2*0 + 1*1 = 8

1110 = 14
4321
4*1 + 3*1 + 2*1 + 1*0 = 9

1111 = 15
4321
4*1 + 3*1 + 2*1 + 1*1 = 10

10000 = 16
54321
5*1 + 4*0 + 3*0 + 2*0 + 1*0 = 5


In that sequence, although no number occurs infinitely often, some numbers occur more often than others. If you represent the count of sums up to a certain digit-length as a graph, you get a famous shape:

Bell curve formed by the count of column-sums in base 2

Bi-bell curves for 1 to 16 binary digits (animated)

In “Pi in the Bi”, I looked at that way of forming the bell curve and called it the bi-bell curve. Now I want to go further. Suppose that you assign varying values to the columns and try other bases. For example, what happens if you assign the values 2^p + 1 to the columns, reading from right to left, then use base 3 to generate the sums? These are the values of 2^p + 1:

2, 3, 5, 9, 17, 33, 65, 129, 257, 513, 1025...


And here’s an example of how you generate a column-sum in base 3:

2102 in base 3 = 65 in base ten
9532 (column values from right to left)
2*9 + 1*5 + 0*3 + 2*2 = 27


The graphs for these column-sums using base 3 look like this as the digit-length rises. They’re no longer bell-curves (and please note that widths and heights have been normalized so that all graphs fit the same space):

Graph for the count of column-sums in base 3 using 2^p + 1 (digit-length <= 7)

(width and height are normalized)

Graph for base 3 and 2^p + 1 (dl<=8)

Graph for base 3 and 2^p + 1 (dl<=9)

Graph for base 3 and 2^p + 1 (dl<=10)

Graph for base 3 and 2^p + 1 (dl<=11)

Graph for base 3 and 2^p + 1 (dl<=12)

Graph for base 3 and 2^p + 1 (animated)

Now try base 3 and column-values of 2^p + 2 = 3, 4, 6, 10, 18, 34, 66, 130, 258, 514, 1026…

Graph for base 3 and 2^p + 2 (dl<=7)

Graph for base 3 and 2^p + 2 (dl<=8)

Graph for base 3 and 2^p + 2 (dl<=9)

Graph for base 3 and 2^p + 2 (dl<=10)

Graph for base 3 and 2^p + 2 (animated)

Now try base 5 and 2^p + 1 for the columns. The original bell curve has become like a fractal called the blancmange curve:

Graph for base 5 and 2^p + 1 (dl<=7)

Graph for base 5 and 2^p + 1 (dl<=8)

Graph for base 5 and 2^p + 1 (dl<=9)

Graph for base 5 and 2^p + 1 (dl<=10)

Graph for base 5 and 2^p + 1 (animated)

And finally, return to base 2 and try the Fibonacci numbers for the columns:

Graph for base 2 and Fibonacci numbers = 1,1,2,3,5… (dl<=7)

Graph for base 2 and Fibonacci numbers (dl<=9)

Graph for base 2 and Fibonacci numbers (dl<=11)

Graph for base 2 and Fibonacci numbers (dl<=13)

Graph for base 2 and Fibonacci numbers (dl<=15)

Graph for base 2 and Fibonacci numbers (animated)

Previously Pre-Posted…

• Pi in the Bi — bell curves generated by binary digits