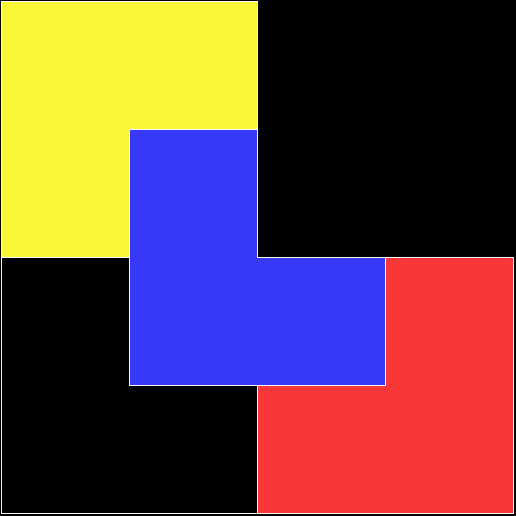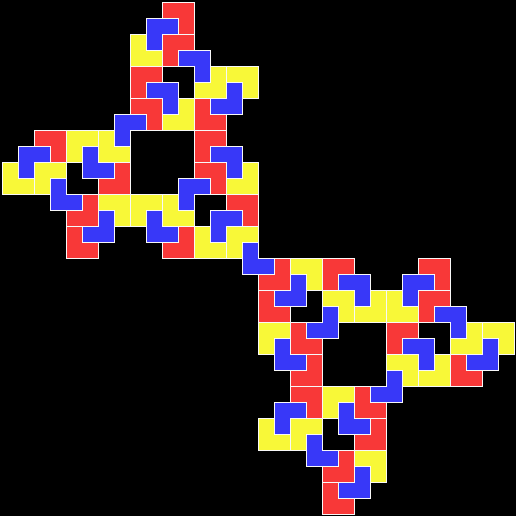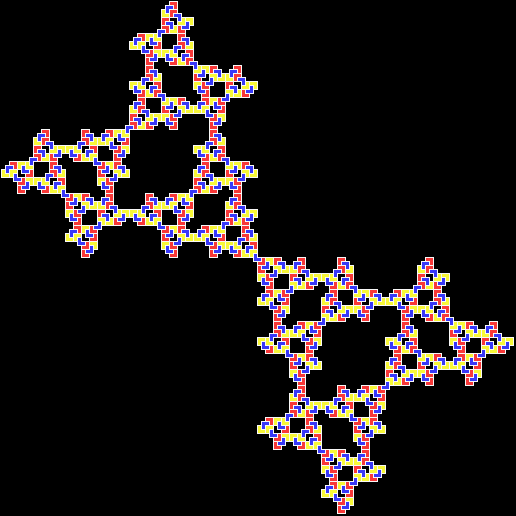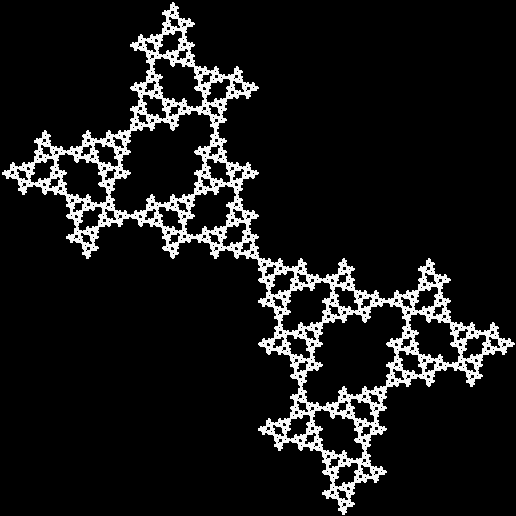Category Archives: Fractals
Curious Cuneus
Monteverde’s Mathemorphosis
Here are some fractals based on the Angelo di Monteverde or Angelo della Resurrezione carved by the Italian sculptor Giulio Monteverde (1837-1917) for the monumental cemetery of Staglieno in Genoa.
Jug is the Drug
In “The Gems of Rebbuqqa”, I interrogated notions around the concept of priestesses who permanently juggle three giant eye-like gems, a ruby, a sapphire, and an emerald, atop a sandstone altar. In “The Schismatarch” (forthcoming), I will interrogate notions around the concept of a Himalayan sect that believes this universe is one of three juggled by a god called Nganāma. Each of these universes contains a smaller Nganāma who juggles three dwarf universes; et sic ad infinitum. Moreover, the Nganāma juggling our universe sits in a larger universe, one of three juggled by a giant Nganāma in a larger universe still, which is one of three on a higher plane; et sic ad infinitum. The cosmology of the Nganāma-sect is fractal: ut supra, sic infra: as above, so below. Here are some animated gifs inspired by these two stories and based on juggled eye-gem fractals.

Rep-Tiles Revisited
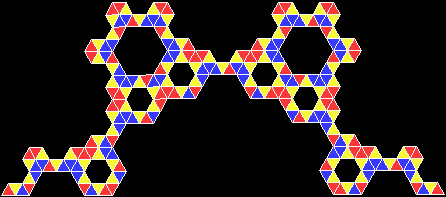
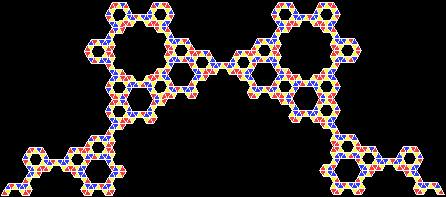
A Feast of Fractiles
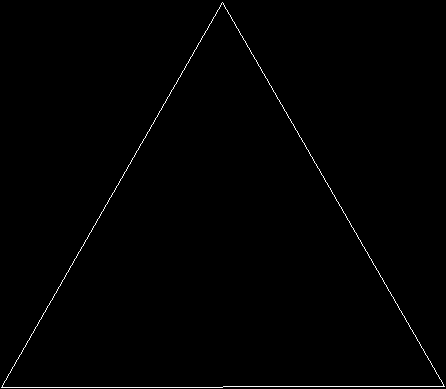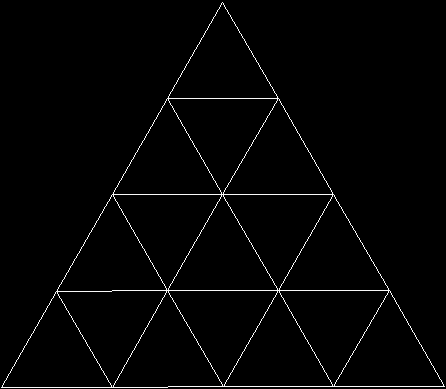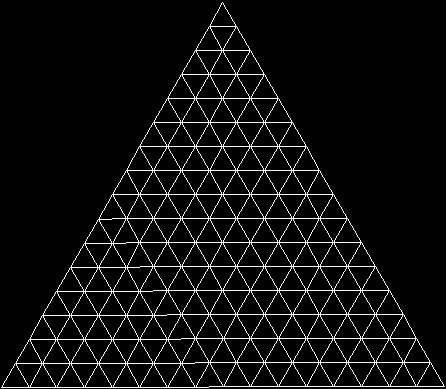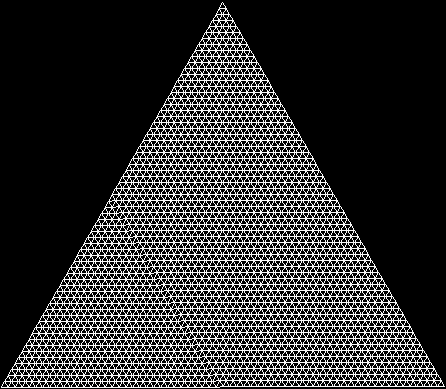
A rep-tile is a shape that can be divided into copies of itself. One of the simplest rep-tiles is the equilateral triangle, which can be divided into four copies of itself, like this:
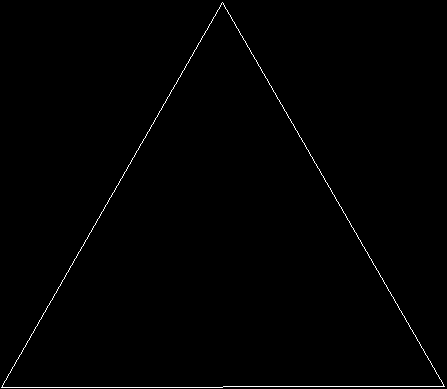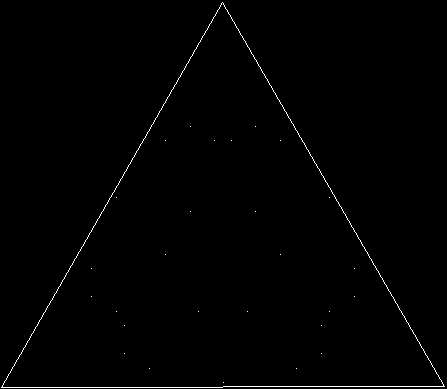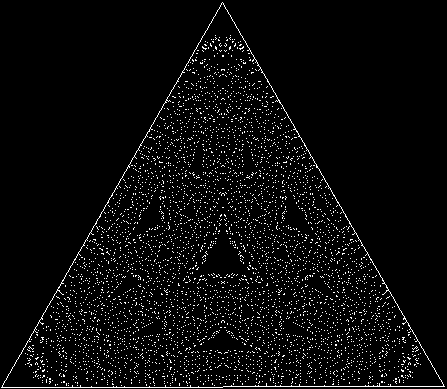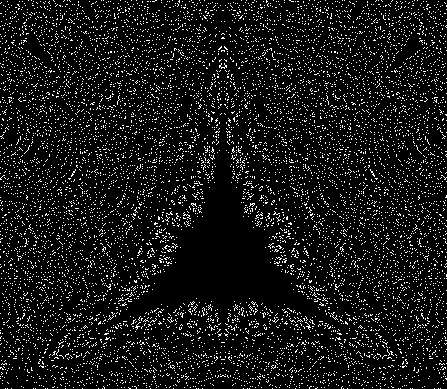
If, on the other hand, the triangle is subdivided and then one of the copies is discarded, many interesting fractals can be made from this very simple shape:
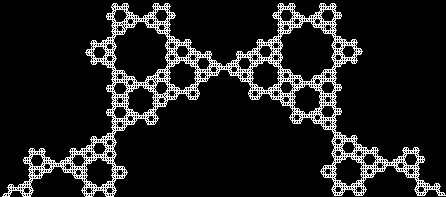
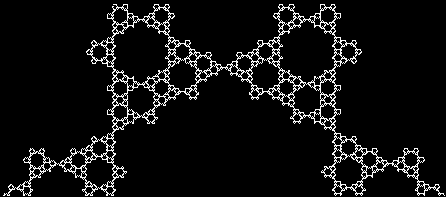
This sequence illustrates how a more complex fractal is created:
And here is the sequence in a single animated gif: