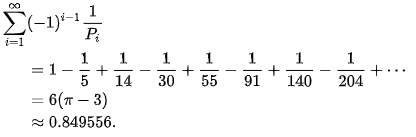Matching Fractions

Sunday, 29th Jun, 2025 by Krilling for Company in Arithmetic, Base Behavior, Mathematics and tagged base 10, base 11, base 12, base 8, base 9, decimal fractions, fractions, matching digits, octal, recreational math, recreational mathematics, recreational maths | Leave a comment

0.1666… = 1/6
0.0273972… = 2/73
0.0379746… = 3/79
0.0016181229… = 1/618
0.0027322404… = 2/732 → 1/366
0.0058548009… = 5/854
0.01393354769… = 13/933
0.07598784194… = 75/987 → 25/329
0.08998988877… = 89/989
0.141993957703… = 141/993 → 47/331
0.0005854115443… = 5/8541
0.00129282482223… = 12/9282 → 2/1547
0.00349722279366… = 34/9722 → 17/4861
0.013599274705349… = 135/9927 → 15/1103
0.0000273205382146… = 2/73205

0.0465103… = 4/65 in base 8 = 4/53 in base 10
0.13735223… = 13/73 in b8 = 11/59 in b10
0.0036256353… = 3/625 → 1/207 in b8 = 3/405 → 1/135 in b10
0.01172160236… = 11/721 → 3/233 in b8 = 9/465 → 3/155 in b10
0.01272533117… = 12/725 in b8 = 10/469 in b10
0.03175523464… = 31/755 in b8 = 25/493 in b10
0.06776766655… = 67/767 in b8 = 55/503 in b10
0.251775771755… = 251/775 in b8 = 169/509 in b10
0.0003625152504… = 3/6251 in b8 = 3/3241 in b10
0.00137303402723… = 13/7303 in b8 = 11/3779 in b10
0.00267525714052… = 26/7525 in b8 = 22/3925 in b10
0.035777577356673… = 357/7757 in b8 = 239/4079 in b10

0.3763… = 3/7 in b9 = 3/7 in b10
0.0155187… = 1/55 in b9 = 1/50 in b10
0.0371482… = 3/71 in b9 = 3/64 in b10
0.0474627… = 4/74 in b9 = 4/67 in b10
0.43878684… = 43/87 in b9 = 39/79 in b10
0.07887877766… = 78/878 in b9 = 71/719 in b10
0.01708848667… = 17/0884 → 4/221 in b9 = 16/724 → 4/181 in b10
0.170884866767… = 170/884 → 40/221 in b9 = 144/724 → 36/181 in b10

0.2828… = 2/8 → 1/4 in b11 = 2/8 → 1/4 in b10
0.4986… = 4/9 in b11 = 4/9 in b10
0.54A9A8A6… = 54/A9 in b11 = 59/119 in b10
0.0010A17039… = 1/A17 in b11 = 1/1228 in b10
0.010A170392A… = 10/A17 in b11 = 11/1228 in b10
0.01AA5854872… = 1A/A58 in b11 = 21/1273 in b10
0.027A716A416… = 27/A71 in b11 = 29/1288 in b10
0.032A78032A7… = 32/A78 → 1/34 in b11 = 35/1295 → 1/37 in b10
0.0190AA5A829… = 19/0AA5 → 4/221 in b11 = 20/1325 → 4/265 in b10
0.190AA5A829… = 190/AA5 → 40/221 in b11 = 220/1325 → 44/265 in b10

0.23B7A334… = 23/B7 in b12 = 27/139 in b10
0.075BA597224… = 75/BA5 in b12 = 89/1709 in b10
0.0ABBABAAA99… = AB/BAB in b12 = 131/1715 in b10
0.185BB5B859B4… = 185/BB5 in b12 = 245/1721 in b10

Pyramidic Palindromes

Tuesday, 17th Oct, 2023 by Krilling for Company in Base Behavior, Integer Sequences, π, Mathematics, Palindromic numbers, Pi, Powers, Squares and tagged base 10, base 9, cannonballs, cubic pyramidal numbers, East Sussex, palindromes, pi, pile of cannonballs, Rye Castle, square pyramidal numbers, sum of cubes, sum of squares | Leave a comment

As I’ve said before on Overlord of the Über-Feral: squares are boring. As I’ve shown before on Overlord of the Über-Feral: squares are not so boring after all.

Take A000330 at the Online Encyclopedia of Integer Sequences:

1, 5, 14, 30, 55, 91, 140, 204, 285, 385, 506, 650, 819, 1015, 1240, 1496, 1785, 2109, 2470, 2870, 3311, 3795, 4324, 4900, 5525, 6201, 6930, 7714, 8555, 9455, 10416, 11440, 12529, 13685, 14910, 16206, 17575, 19019, 20540, 22140, 23821, 25585, 27434, 29370… — A000330 at OEIS

The sequence shows the square pyramidal numbers, formed by summing the squares of integers:

• 1 = 1^2
• 5 = 1^2 + 2^2 = 1 + 4
• 14 = 1^2 + 2^2 + 3^2 = 1 + 4 + 9
• 30 = 1^2 + 2^2 + 3^2 + 4^2 = 1 + 4 + 9 + 16

[…]

You can see the pyramidality of the square pyramidals when you pile up oranges or cannonballs:

Square pyramid of 91 cannonballs at Rye Castle, East Sussex (Wikipedia)

I looked for palindromes in the square pyramidals. These are the only ones I could find:

1 (k=1)
5 (k=2)
55 (k=5)
1992991 (k=181)

The only ones in base 10, that is. When I looked in base 9 = 3^2, I got a burst of pyramidic palindromes like this:

1 (k=1)
5 (k=2)
33 (k=4) = 30 in base 10 (k=4)
111 (k=6) = 91 in b10 (k=6)
122221 (k=66) = 73810 in b10 (k=60)
123333321 (k=666) = 54406261 in b10 (k=546)
123444444321 (k=6,666) = 39710600020 in b10 (k=4920)
123455555554321 (k=66,666) = 28952950120831 in b10 (k=44286)
123456666666654321 (k=666,666) = 21107018371978630 in b10 (k=398580)
123456777777777654321 (k=6,666,666) = 15387042129569911801 in b10 (k=3587226)
123456788888888887654321 (k=66,666,666) = 11217155797104231969640 in b10 (k=32285040)

The palindromic pattern from 6[…]6 ends with 66,666,666, because 8 is the highest digit in base 9. When you look at the 666,666,666th square pyramidal in base 9, you’ll find it’s not a perfect palindrome:

123456801111111111087654321 (k=666,666,666) = 8177306744945450299267171 in b10 (k=290565366)

But the pattern of pyramidic palindromes is good while it lasts. I can’t find any other base yielding a pattern like that. And base 9 yields another burst of pyramidic palindromes in a related sequence, A000537 at the OEIS:

1, 9, 36, 100, 225, 441, 784, 1296, 2025, 3025, 4356, 6084, 8281, 11025, 14400, 18496, 23409, 29241, 36100, 44100, 53361, 64009, 76176, 90000, 105625, 123201, 142884, 164836, 189225, 216225, 246016, 278784, 314721, 354025, 396900, 443556, 494209, 549081… — A000537 at OEIS

The sequence is what you might call the cubic pyramidal numbers, that is, the sum of the cubes of integers:

• 1 = 1^2
• 9 = 1^2 + 2^3 = 1 + 8
• 36 = 1^3 + 2^3 + 3^3 = 1 + 8 + 27
• 100 = 1^3 + 2^3 + 3^3 + 4^3 = 1 + 8 + 27 + 64

[…]

I looked for palindromes there in base 9:

1 (k=1) = 1 (k=1)
121 (k=4) = 100 in base 10 (k=4)
12321 (k=14) = 8281 (k=13)
1234321 (k=44) = 672400 (k=40)
123454321 (k=144) = 54479161 (k=121)
12345654321 (k=444) = 4412944900 (k=364)
1234567654321 (k=1444) = 357449732641 (k=1093)
123456787654321 (k=4444) = 28953439105600 (k=3280)
102012022050220210201 (k=137227) = 12460125198224404009 (k=84022)

But while palindromes are fun, they’re not usually mathematically significant. However, this result using the square pyrmidals is certainly significant:

Previously Pre-Posted…

More posts about how squares aren’t so boring after all:

• Curvous Energy
• Back to Drac #1
• Back to Drac #2
• Square’s Flair

Nuts for Numbers

Friday, 22nd Sep, 2023 by Krilling for Company in Arithmetic, Base Behavior, Integer Sequences, Mathematics and tagged 210, 2772, Arithmetic, base 10, base 8, base 9, integer sums, Mr Logic, Mr Logic and nuts, nuts, nutty numbers, nutty sums, palindromes, recreational math, recreational mathematics, recreational maths, summing integers, sums of consecutive integers, Viz, Viz comic | Leave a comment

I was looking at palindromes created by sums of consecutive integers. And I came across this beautiful result:

2772 = sum(22..77)

2772 = 22 + 23 + 24 + 25 + 26 + 27 + 28 + 29 + 30 + 31 + 32 + 33 + 34 + 35 + 36 + 37 + 38 + 39 + 40 + 41 + 42 + 43 + 44 + 45 + 46 + 47 + 48 + 49 + 50 + 51 + 52 + 53 + 54 + 55 + 56 + 57 + 58 + 59 + 60 + 61 + 62 + 63 + 64 + 65 + 66 + 67 + 68 + 69 + 70 + 71 + 72 + 73 + 74 + 75 + 76 + 77

You could call 2772 a nutty sum, because 77 is held inside 22 like a kernel inside a nutshell. Here some more nutty sums, sum(n₁..n₂), where n₂ is a kernel in the shell of n₁:

1599 = sum(19..59)
2772 = sum(22..77)
22113 = sum(23..211)
159999 = sum(199..599)
277103 = sum(203..771)
277722 = sum(222..777)
267786 = sum(266..778)
279777 = sum(277..797)
1152217 = sum(117..1522)
1152549 = sum(149..1525)
1152767 = sum(167..1527)
4296336 = sum(436..2963)
5330303 = sum(503..3303)
6235866 = sum(626..3586)
8418316 = sum(816..4183)
10470075 = sum(1075..4700)
11492217 = sum(1117..4922)
13052736 = sum(1306..5273)
13538277 = sum(1377..5382)
14557920 = sum(1420..5579)
15999999 = sum(1999..5999)
25175286 = sum(2516..7528)
26777425 = sum(2625..7774)
27777222 = sum(2222..7777)
37949065 = sum(3765..9490)
53103195 = sum(535..10319)
111497301 = sum(1101..14973)

Of course, you can go the other way and find nutty sums where sum(n₁..n₂) produces n₁ as a kernel inside the shell of n₂:

147 = sum(4..17)
210 = sum(1..20)
12056 = sum(20..156)
13467 = sum(34..167)
22797 = sum(79..227)
22849 = sum(84..229)
26136 = sum(61..236)
1145520 = sum(145..1520)
1208568 = sum(208..1568)
1334667 = sum(334..1667)
1540836 = sum(540..1836)
1931590 = sum(315..1990)
2041462 = sum(414..2062)
2041863 = sum(418..2063)
2158083 = sum(158..2083)
2244132 = sum(244..2132)
2135549 = sum(554..2139)
2349027 = sum(902..2347)
2883558 = sum(883..2558)
2989637 = sum(989..2637)

When you look at nutty sums in other bases, you’ll find that the number “210” is always triangular and always a nutty sum in bases > 2:

210 = sum(1..20) in b3 → 21 = sum(1..6) in b10
210 = sum(1..20) in b4 → 36 = sum(1..8) in b10
210 = sum(1..20) in b5 → 55 = sum(1..10) in b10
210 = sum(1..20) in b6 → 78 = sum(1..12) in b10
210 = sum(1..20) in b7 → 105 = sum(1..14) in b10
210 = sum(1..20) in b8 → 136 = sum(1..16) in b10
210 = sum(1..20) in b9 → 171 = sum(1..18) in b10
210 = sum(1..20) in b10
210 = sum(1..20) in b11 → 253 = sum(1..22) in b10
210 = sum(1..20) in b12 → 300 = sum(1..24) in b10
210 = sum(1..20) in b13 → 351 = sum(1..26) in b10
210 = sum(1..20) in b14 → 406 = sum(1..28) in b10
210 = sum(1..20) in b15 → 465 = sum(1..30) in b10
210 = sum(1..20) in b16 → 528 = sum(1..32) in b10
210 = sum(1..20) in b17 → 595 = sum(1..34) in b10
210 = sum(1..20) in b18 → 666 = sum(1..36) in b10
210 = sum(1..20) in b19 → 741 = sum(1..38) in b10
210 = sum(1..20) in b20 → 820 = sum(1..40) in b10
[…]

Why is 210 always a nutty sum like that? Because the formula for sum(n₁..n₂) is (n₁*n₂) * (n₂-n₁+1) / 2. In all bases > 2, the sum of 1 to 20 (where 20 = 2 * b) is therefore:

(1+20) * (20-1+1) / 2 = 21 * 20 / 2 = 21 * 10 = 210

And here are nutty sums of both kinds (n₁ inside n₂ and n₂ inside n₁) for base 8:

210 = sum(1..20) in b8 → 136 = sum(1..16) in b10
12653 = sum(26..153) → 5547 = sum(22..107)
23711 = sum(71..231) → 10185 = sum(57..153)
2022323 = sum(223..2023) → 533715 = sum(147..1043)
2032472 = sum(247..2032) → 537914 = sum(167..1050)
2271564 = sum(715..2264) → 619380 = sum(461..1204)
2307422 = sum(742..2302) → 626450 = sum(482..1218)
125265253 = sum(2526..15253) → 22375083 = sum(1366..6827)

3246710 = sum(310..2467) in b8 → 871880 = sum(200..1335)
in b10
5326512 = sum(512..3265) → 1420618 = sum(330..1717)
15540671 = sum(1571..5406) → 3588537 = sum(889..2822)
21625720 = sum(2120..6257) → 4664272 = sum(1104..3247)

And for base 9:

125 = sum(2..15) in b9 → 104 = sum(2..14) in b10
210 = sum(1..20) → 171 = sum(1..18)
12858 = sum(28..158) → 8720 = sum(26..134)
1128462 = sum(128..1462) → 609824 = sum(107..1109)
1288588 = sum(288..1588) → 708344 = sum(242..1214)
1475745 = sum(475..1745) → 817817 = sum(392..1337)
2010707 = sum(107..2007) → 1070017 = sum(88..1465)
2034446 = sum(344..2046) → 1085847 = sum(283..1500)
2040258 = sum(402..2058) → 1089341 = sum(326..1511)
2063410 = sum(341..2060) → 1104768 = sum(280..1512)
2215115 = sum(215..2115) → 1191281 = sum(176..1553)
2255505 = sum(555..2205) → 1217840 = sum(455..1625)
2475275 = sum(475..2275) → 1348880 = sum(392..1688)
2735455 = sum(735..2455) → 1499927 = sum(599..1832)

1555 = sum(15..55) in b9 → 1184 = sum(14..50) in b10
155858 = sum(158..558) → 96200 = sum(134..458)
1148181 = sum(181..1481) → 622720 = sum(154..1126)
2211313 = sum(213..2113) → 1188525 = sum(174..1551)
2211747 = sum(247..2117) → 1188880 = sum(205..1555)
6358585 = sum(685..3585) → 3404912 = sum(563..2669)
7037453 = sum(703..3745) → 3745245 = sum(570..2795)
7385484 = sum(784..3854) → 3953767 = sum(643..2884)
13518167 = sum(1367..5181) → 6685072 = sum(1033..3799)
15588588 = sum(1588..5588) → 7794224 = sum(1214..4130)
17603404 = sum(1704..6034) → 8859865 = sum(1300..4405)
26750767 = sum(2667..7507) → 13201360 = sum(2005..5515)

Post-Performative Post-Scriptum…

Viz ’s Mr Logic would be a fan of nutty sums. And unlike real nuts, they wouldn’t prove fatal:

Mr Logic Goes Nuts (strip from Viz comic)

(click for full-size)

Palindrought

Tuesday, 17th Aug, 2021 by Krilling for Company in Base Behavior, Integer Sequences, Mathematics, Palindromic numbers and tagged base 10, base 9, Integer Sequences, integers, math, mathematics, maths, palindromes, palindromic numbers, recreational math, recreational mathematics, recreational maths, Square Numbers, sums of palindromes, Triangular Numbers | Leave a comment

The alchemists dreamed of turning dross into gold. In mathematics, you can actually do that, metaphorically speaking. If palindromes are gold and non-palindromes are dross, here is dross turning into gold:

22 = 10 + 12 222 = 10 + 12 + 13 + 14 + 15 + 16 + 17 + 18 + 19 + 20 + 23 + 24 484 = 10 + 12 + 13 + 14 + 15 + 16 + 17 + 18 + 19 + 20 + 21 + 23 + 24 + 25 + 26 + 27 + 28 + 29 + 30 + 31 + 32 + 34 555 = 10 + 12 + 13 + 14 + 15 + 16 + 17 + 18 + 19 + 20 + 21 + 23 + 24 + 25 + 26 + 27 + 28 + 29 + 30 + 31 + 32 + 34 + 35 + 36 2002 = nonpalsum(10,67) 36863 = nonpalsum(10,286) 45954 = nonpalsum(10,319) 80908 = nonpalsum(10,423) 113311 = nonpalsum(10,501) 161161 = nonpalsum(10,598) 949949 = nonpalsum(10,1417) 8422248 = nonpalsum(10,4136) 13022031 = nonpalsum(10,5138) 14166141 = nonpalsum(10,5358) 16644661 = nonpalsum(10,5806) 49900994 = nonpalsum(10,10045) 464939464 = nonpalsum(10,30649) 523434325 = nonpalsum(10,32519) 576656675 = nonpalsum(10,34132) 602959206 = nonpalsum(10,34902) [...]

The palindromes don’t seem to stop arriving. But something unexpected happens when you try to turn gold into gold. If you sum palindromes to get palindromes, you’re soon hit by what you might call a palindrought, where no palindromes appear:

1 = 1 3 = 1 + 2 6 = 1 + 2 + 3 111 = 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 11 + 22 + 33 353 = 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 11 + 22 + 33 + 44 + 55 + 66 + 77 7557 = 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 11 + 22 + 33 + 44 + 55 + 66 + 77 + 88 + 99 + 101 + 111 + 121 + 131 + 141 + 151 + 161 + 171 + 181 + 191 + 202 + 212 + 222 + 232 + 242 + 252 + 262 + 272 + 282 + 292 + 303 + 313 + 323 + 333 + 343 + 353 + 363 + 373 + 383 2376732 = palsum(1,21512)

That’s sequence A046488 at the OEIS. And I suspect that the sequence is complete and that the palindrought never ends. For some evidence of that, here’s an interesting pattern that emerges if you look at palsums of 1 to repdigits 9[…]9:

50045040 = palsum(1,99999) 50045045040 = palsum(1,9999999) 50045045045040 = palsum(1,999999999) 50045045045045040 = palsum(1,99999999999) 50045045045045045040 = palsum(1,9999999999999) 50045045045045045045040 = palsum(1,999999999999999) 50045045045045045045045040 = palsum(1,99999999999999999) 50045045045045045045045045040 = palsum(1,9999999999999999999) 50045045045045045045045045045040 = palsum(1,999999999999999999999)

As the sums get bigger, the carries will stop sweeping long enough and the sums may fall into semi-regular patterns of non-palindromic numbers like 50045040. If you try higher bases like base 909, you get more palindromes by summing palindromes, but a palindrought arrives in the end there too:

1 = palsum(1) 3 = palsum(1,2) 6 = palsum(1,3) A = palsum(1,4) [...] 66 = palsum(1,[104]) (palindromes = 43) LL = palsum(1,[195]) (44) [37][37] = palsum(1,[259]) (45) [73][73] = palsum(1,[364]) (46) [114][114] = palsum(1,[455]) (47) [172][172] = palsum(1,[559]) (48) [369][369] = palsum(1,[819]) (49) 6[466]6 = palsum(1,[104][104]) (50) L[496]L = palsum(1,[195][195]) (51) [37][528][37] = palsum(1,[259][259]) (52) [73][600][73] = palsum(1,[364][364]) (53) [114][682][114] = palsum(1,[455][455]) (54) [172][798][172] = palsum(1,[559][559]) (55) [291][126][291] = palsum(1,[726][726]) (56) [334][212][334] = palsum(1,[778][778]) (57) [201][774][830][774][201] = palsum(1,[605][707][605]) (58) [206][708][568][708][206] = palsum(1,[613][115][613]) (59) [456][456][569][569][456][456] = palsum(1,11[455]11) (60) 22[456][454][456]22 = palsum(1,21012) (61)

Note the palindrome for palsum(1,21012). All odd bases higher than 3 seem to produce a palindrome for 1 to 21012 in that base (21012 in base 5 = 1382 in base 10, 2012 in base 7 = 5154 in base 10, and so on):

2242422 = palsum(1,21012) (base=5) 2253522 = palsum(1,21012) (b=7) 2275722 = palsum(1,21012) (b=11) 2286822 = palsum(1,21012) (b=13) 2297922 = palsum(1,21012) (b=15) 22A8A22 = palsum(1,21012) (b=17) 22B9B22 = palsum(1,21012) (b=19) 22CAC22 = palsum(1,21012) (b=21) 22DBD22 = palsum(1,21012) (b=23)

And here’s another interesting pattern created by summing squares in base 9 (where 17 = 16 in base 10, 40 = 36 in base 10, and so on):

1 = squaresum(1) 5 = squaresum(1,4) 33 = squaresum(1,17) 111 = squaresum(1,40) 122221 = squaresum(1,4840) 123333321 = squaresum(1,503840) 123444444321 = squaresum(1,50483840) 123455555554321 = squaresum(1,5050383840) 123456666666654321 = squaresum(1,505048383840) 123456777777777654321 = squaresum(1,50505038383840) 123456788888888887654321 = squaresum(1,5050504838383840)

Then a palindrought strikes again. But you don’t get a palindrought in the triangular numbers, or numbers created by summing the integers, palindromic and non-palindromic alike:

1 = 1 3 = 1 + 2 6 = 1 + 2 + 3 55 = 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 66 = 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 + 11 171 = 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 + 11 + 12 + 13 + 14 + 15 + 16 + 17 + 18 595 = 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 + 11 + 12 + 13 + 14 + 15 + 16 + 17 + 18 + 19 + 20 + 21 + 22 + 23 + 24 + 25 + 26 + 27 + 28 + 29 + 30 + 31 + 32 + 33 + 34 666 = 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 + 11 + 12 + 13 + 14 + 15 + 16 + 17 + 18 + 19 + 20 + 21 + 22 + 23 + 24 + 25 + 26 + 27 + 28 + 29 + 30 + 31 + 32 + 33 + 34 + 35 + 36 3003 = palsum(1,77) 5995 = palsum(1,109) 8778 = palsum(1,132) 15051 = palsum(1,173) 66066 = palsum(1,363) 617716 = palsum(1,1111) 828828 = palsum(1,1287) 1269621 = palsum(1,1593) 1680861 = palsum(1,1833) 3544453 = palsum(1,2662) 5073705 = palsum(1,3185) 5676765 = palsum(1,3369) 6295926 = palsum(1,3548) 35133153 = palsum(1,8382) 61477416 = palsum(1,11088) 178727871 = palsum(1,18906) 1264114621 = palsum(1,50281) 1634004361 = palsum(1,57166) 5289009825 = palsum(1,102849) 6172882716 = palsum(1,111111) 13953435931 = palsum(1,167053) 16048884061 = palsum(1,179158) 30416261403 = palsum(1,246642) 57003930075 = palsum(1,337650) 58574547585 = palsum(1,342270) 66771917766 = palsum(1,365436) 87350505378 = palsum(1,417972) [...]

If 617716 = palsum(1,1111) and 6172882716 = palsum(1,111111), what is palsum(1,11111111)? Try it for yourself — there’s an easy formula for the triangular numbers.

Can You Dij It? #1

Monday, 29th Feb, 2016 by Krilling for Company in Base Behavior, Binary numbers, Integer Sequences, Mathematics and tagged almost natural numbers, assembly language, base 10, base 9, binary, computers, decimal, digits, drugs, electronics, Integer Sequences, Language, machine code, math, mathemagic, mathemagick, mathematics, maths, natural languages, numbers, OEIS, Online Encyclopedia of Integer Sequences, reality, recreational math, recreational mathematics, recreational maths, water | 2 Comments

The most powerful drug in the world is water. The second most powerful is language. But everyone’s on them, so nobody realizes how powerful they are. Well, you could stop drinking water. Then you’d soon realize its hold on the body and the brain.

But you can’t stop using language. Try it. No, the best way to realize the power of language is to learn a new one. Each is a feast with different flavours. New alphabets are good too. The Devanagari alphabet is one of the strongest, but if you want it in refined form, try the phonetic alphabet. It will transform the way you see the world. That’s because it will make you conscious of what you’re already subconsciously aware of.

But “language” is a bigger category that it used to be. Nowadays we have computer languages too. Learning one is another way of transforming the way you see the world. And like natural languages – French, Georgian, Tagalog – they come in different flavours. Pascal is not like Basic is not like C is not like Prolog. But all of them seem to put you in touch with some deeper aspect of reality. Computer languages are like mathemagick: a way to give commands to something immaterial and alter the world by the application of will.

That feeling is at its strongest when you program with machine code, the raw instructions used by the electronics of a computer. At its most fundamental, machine code is simply a series of binary numbers controlling how a computer processes other binary numbers. You can memorize and use those code-numbers, but it’s easier to use something like assembly language, which makes machine-code friendlier for human beings. But it still looks very odd to the uninitiated:

setupnum:
xor ax,ax
xor bp,bp
mov cx,20
clearloop:
mov [di+bp],ax
add bp,2
loop clearloop
ret

That’s almost at the binary bedrock. And machine code is fast. If a fast higher-level language like C feels like flying a Messerschmitt 262, which was a jet-plane, machine-code feels like flying a Messerschmitt 163, which was a rocket-plane. A very fast and very dangerous rocket-plane.

I’m not good at programming languages, least of all machine code, but they are fun to use, quite apart from the way they make you feel as though you’re in touch with a deeper aspect of reality. They do that because the world is mathematics at its most fundamental level, I think, and computer languages are a form of mathematics.

Their mathematical nature is disguised in a lot of what they’re used for, but I like to use them for recreational mathematics. Machine-code is useful when you need a lot of power and speed. For example, look at these digits:

1, 2, 3, 4, 5, 6, 7, 8, 9, 1*, 0*, 1, 1, 1, 2, 1, 3, 1, 4, 1, 5, 1, 6, 1, 7, 1, 8, 1, 9, 2, 0, 2, 1, 2, 2, 2, 3, 2, 4, 2, 5, 2, 6, 2, 7, 2, 8, 2, 9, 3, 0, 3, 1, 3, 2, 3, 3, 3, 4, 3, 5, 3, 6*, 3*, 7, 3, 8, 3, 9, 4, 0, 4, 1, 4, 2, 4…

They’re what the Online Encyclopedia of Integer Sequences (OEIS) calls “the almost natural numbers” (sequence A007376) and you generate them by writing the standard integers – 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13… – and then separating each digit with a comma: 1, 2, 3, 4, 5, 6, 7, 8, 9, 1, 0, 1, 1, 1, 2, 1, 3… The commas give them some interesting twists. In a list of the standard integers, the 1st entry is 1, the 10th entry is 10, the 213rd entry is 213, the 987,009,381th entry is 987,009,381, and so on.

But that doesn’t work with the almost natural numbers. The 10th entry is 1, not 10, and the 11th entry is 0, not 11. But the 10th entry does begin the sequence (1, 0). I wondered whether that happened again. It does. The 63rd entry in the almost natural numbers begins the sequence (6, 3) – see the asterisks in the sequence above.

This happens again at the 3105th entry, which begins the sequence (3, 1, 0, 5). After that the gaps get bigger, which is where machine code comes in. An ordinary computer-language takes a long time to reach the 89,012,345,679th entry in the almost natural numbers. Machine code is much quicker, which is why I know that the 89,012,345,679th entry begins the sequence (8, 9, 0, 1, 2, 3, 4, 5, 6, 7, 9):

1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 63, 3105, 43108, 77781, 367573, 13859021, 77911127, 911360799, 35924813703, 74075186297, 89012345679…

And an ordinary computer-language might give you the impression that base 9 doesn’t have numbers like these (apart from the trivial 1, 2, 3, 4, 5, 6, 7, 8, 10…). But it does. 63 in base 10 is a low-hanging fruit: you could find it working by hand. In base 9, the fruit are much higher-hanging. But machine code plucks them with almost ridiculous ease:

1, 2, 3, 4, 5, 6, 7, 8, 10, 570086565, 655267526, 2615038272, 4581347024, 5307541865, 7273850617, 7801234568…

Narcischism

Thursday, 9th Apr, 2015 by Krilling for Company in Binary numbers, Mathematics, Narcissistic numbers and tagged addition, Arithmetic, base 10, base 2, base 4, base 5, base 6, base 7, base 8, base 9, binary, binary numbers, digits, integers, math, mathematics, maths, narcischism, narcischist, narcischistic numbers, narcissistic numbers, numbers, recreational math, recreational mathematics, recreational maths, split bit digits, split bits, splitting digits, splitting numbers | Leave a comment

What have bits to do with splits? A lot. Suppose you take the digits 12345, split them in all possible ways, then sum the results, like this:

12345 → (1234 + 5) + (123 + 45) + (123 + 4 + 5) + (12 + 345) + (12 + 34 + 5) + (12 + 3 + 45) + (12 + 3 + 4 + 5) + (1 + 2345) + (1 + 234 + 5) + (1 + 23 + 45) + (1 + 23 + 4 + 5) + (1 + 2 + 345) + (1 + 2 + 34 + 5) + (1 + 2 + 3 + 45) + (1 + 2 + 3 + 4 + 5) = 5175.

That’s a sum in base 10, but base 2 is at work below the surface, because each set of numbers is the answer to a series of binary questions: split or not? There are four possible places to split the digits 12345: after the 1, after the 2, after the 3 and after the 4. In (1 + 2 + 3 + 4 + 5), the binary question “Split or not?” is answered SPLIT every time. In (1234 + 5) and (1 + 2345) it’s answered SPLIT only once.

So the splits are governed by a four-digit binary number ranging from 0001 to 1111. When the binary digit is 1, split; when the binary digit is 0, don’t split. In binary, 0001 to 1111 = 01 to 15 in base 10 = 2^4-1. That’s for a five-digit number, so the four-digit 1234 will have 2^3-1 = 7 sets of sums:

1234 → (123 + 4) + (12 + 34) + (12 + 3 + 4) + (1 + 234) + (1 + 23 + 4) + 110 (1 + 2 + 34) + (1 + 2 + 3 + 4) = 502.

And the six-digit number 123456 will have 2^5-1 = 31 sets of sums. By now, an exciting question may have occurred to some readers. Does any number in base 10 equal the sum of all possible numbers formed by splitting its digits?

The exciting answer is: 0. In other words: No. To see why not, examine a quick way of summing the split-bits of 123,456,789, with nine digits. The long way is to find all possible sets of split-bits. There are 2^8-1 = 255 of them. The quick way is to sum these equations:

1 * 128 + 10 * 64 + 100 * 32 + 1000 * 16 + 10000 * 8 + 100000 * 4 + 1000000 * 2 + 10000000 * 1
2 * 128 + 20 * 64 + 200 * 32 + 2000 * 16 + 20000 * 8 + 200000 * 4 + 2000000 * 2 + 20000000 * 1
3 * 128 + 30 * 64 + 300 * 32 + 3000 * 16 + 30000 * 8 + 300000 * 4 + 3000000 * 3
4 * 128 + 40 * 64 + 400 * 32 + 4000 * 16 + 40000 * 8 + 400000 * 7
5 * 128 + 50 * 64 + 500 * 32 + 5000 * 16 + 50000 * 15
6 * 128 + 60 * 64 + 600 * 32 + 6000 * 31
7 * 128 + 70 * 64 + 700 * 63
8 * 128 + 80 * 127
9 * 255

Sum = 52,322,283.

52,322,283 has eight digits. If you use the same formula for the nine-digit number 999,999,999, the sum is 265,621,761, which has nine digits but is far smaller than 999,999,999. If you adapt the formula for the twenty-digit 19,999,999,999,999,999,999 (starting with 1), the split-bit sum is 16,562,499,999,987,400,705. In base 10, as far as I can see, numbers increase too fast and digit-lengths too slowly for the binary governing the split-sums to keep up. That’s also true in base 9 and base 8:

Num = 18,888,888,888,888,888,888 (b=9)
Sum = 16,714,201,578,038,328,760

Num = 17,777,777,777,777,777,777 (b=8)
Sum = 17,070,707,070,625,000,001

So what about base 7? Do the numbers increase slowly enough and the digit-lengths fast enough for the binary to keep up? The answer is: 1. In base 7, this twenty-digit number is actually smaller than its split-bit sum:

Num = 16,666,666,666,666,666,666 (b=7)
Sum = 20,363,036,303,404,141,363

And if you search below that, you can find a number that is equal to its split-bit sum:

166512 → (1 + 6 + 6 + 5 + 1 + 2) + (16 + 6 + 5 + 1 + 2) + (1 + 66 + 5 + 1 + 2) + (166 + 5 + 1 + 2) + (1 + 6 + 65 + 1 + 2) + (16 + 65 + 1 + 2) + (1 + 665 + 1 + 2) + (1665 + 1 + 2) + (1 + 6 + 6 + 51 + 2) + (16 + 6 + 51 + 2) + (1 + 66 + 51 + 2) + (166 + 51 + 2) + (1 + 6 + 651 + 2) + (16 + 651 + 2) + (1 + 6651 + 2) + (16651 + 2) + (1 + 6 + 6 + 5 + 12) + (16 + 6 + 5 + 12) + (1 + 66 + 5 + 12) + (166 + 5 + 12) + (1 + 6 + 65 + 12) + (16 + 65 + 12) + (1 + 665 + 12) + (1665 + 12) + (1 + 6 + 6 + 512) + (16 + 6 + 512) + (1 + 66 + 512) + (166 + 512) + (1 + 6 + 6512) + (16 + 6512) + (1 + 66512) = 166512_[b=7] = 33525_[b=10].

So 33525 in base 7 is what might be called a narcischist: it can gaze into the split-bits of its own digits and see itself gazing back. In base 6, 1940 is a narcischist:

12552 → (1 + 2 + 5 + 5 + 2) + (12 + 5 + 5 + 2) + (1 + 25 + 5 + 2) + (125 + 5 + 2) + (1 + 2 + 55 + 2) + (12 + 55 + 2) + (1 + 255 + 2) + (1255 + 2) + (1 + 2 + 5+ 52) + (12 + 5 + 52) + (1 + 25 + 52) + (125 + 52) + (1 + 2 + 552) + (12 + 552) + (1 + 2552) = 12552_[b=6] = 1940_[b=10].

In base 5, 4074 is a narcischist:

112244 → (1 + 1 + 2 + 2 + 4 + 4) + (11 + 2 + 2 + 4 + 4) + (1 + 12 + 2 + 4 + 4) + (112 + 2 + 4 + 4) + (1 + 1 + 22 + 4 + 4) + (11 + 22 + 4 + 4) + (1 + 122 + 4 + 4) + (1122 + 4 + 4) + (1 + 1 + 2 + 24 + 4) + (11 + 2 + 24 + 4) + (1 + 12 + 24 + 4) + (112 + 24 + 4) + (1 + 1 + 224 + 4) + (11 + 224 + 4) + (1 + 1224 + 4) + (11224 + 4) + (1 + 1 + 2 + 2 + 44) + (11 + 2 + 2 + 44) + (1 + 12 + 2 + 44) + (112 + 2 + 44) + (1 + 1 + 22 + 44) + (11 + 22 + 44) + (1 + 122 + 44) + (1122 + 44) + (1 + 1 + 2 + 244) + (11 + 2 + 244) + (1 + 12 + 244) + (112 + 244) + (1 + 1 + 2244) + (11 + 2244) + (1 + 12244) = 112244_[b=5] = 4074.

And in base 4, 27 is:

123 → (1 + 2 + 3) + (12 + 3) + (1 + 23) = 123_[b=4] = 27.

And in base 3, 13 and 26 are:

111 → (1 + 1 + 1) + (11 + 1) + (1 + 11) = 111_[b=3] = 13.

222 → (2 + 2 + 2) + (22 + 2) + (2 + 22) = 222_[b=3] = 26.

There are many more narcischists in all these bases, even if you exclude numbers with zeroes in them, like these in base 4:

1022 → (1 + 0 + 2 + 2) + (10 + 2 + 2) + (1 + 02 + 2) + (102 + 2) + (1 + 0 + 22) + (10 + 22) + (1 + 022) = 1022_[b=4] = 74.

1030 → (1 + 0 + 3 + 0) + (10 + 3 + 0) + (1 + 03 + 0) + (103 + 0) + (1 + 0 + 30) + (10 + 30) + (1 + 030) = 1030_[b=4] = 76.

1120 → (1 + 1 + 2 + 0) + (11 + 2 + 0) + (1 + 12 + 0) + (112 + 0) + (1 + 1 + 20) + (11 + 20) + (1 + 120) = 1120_[b=4] = 88.

Magistra Rules the Waves

Monday, 30th Mar, 2015 by Krilling for Company in Base Behavior, Binary numbers, Digit-sums, Integer Sequences, Magistra Mundi, Mathematics and tagged base 10, base 13, base 16, base 17, base 2, base 25, base 33, base 49, base 9, digit sum, digit sums, integer patterns, Integer Sequences, integer spirals, integers, math, mathematics, maths, number patterns, primes, randomness, recreational math, recreational mathematics, recreational maths, regularity, spiral of integers, Square Numbers, Squares, Ulam Spirals | Leave a comment

One of my favourite integer sequences has the simple formula n(i) = n(i-1) + digitsum(n(i-1)). If it’s seeded with 1, its first few terms go like this:

n(1) = 1
n(2) = n(1) + digitsum(n(1)) = 1 + digitsum(1) = 2
n(3) = 2 + digitsum(2) = 4
n(4) = 4 + digitsum(4) = 8
n(5) = 8 + digitsum(8) = 16
n(6) = 16 + digitsum(16) = 16 + 1+6 = 16 + 7 = 23
n(7) = 23 + digitsum(23) = 23 + 2+3 = 23 + 5 = 28
n(8) = 28 + digitsum(28) = 28 + 2+8 = 28 + 10 = 38

As a sequence, it looks like this:

1, 2, 4, 8, 16, 23, 28, 38, 49, 62, 70, 77, 91, 101, 103, 107, 115, 122, 127, 137, 148, 161, 169, 185, 199, 218, 229, 242, 250, 257, 271, 281, 292, 305, 313, 320, 325, 335, 346, 359, 376, 392, 406, 416, 427, 440, 448, 464, 478, 497, 517, 530, 538, 554, 568, 587, 607, 620, 628, 644, 658, 677, 697, 719, 736, 752, 766, 785, 805, 818, 835, 851, 865, 884, 904, 917, 934, 950, 964, 983, 1003…

Given a number at random, is there a quick way to say whether it appears in the sequence seeded with 1? Not that I know, with one exception. If the number is divisible by 3, it doesn’t appear, at least in base 10. In base 2, that rule doesn’t apply:

n(1) = 1
n(2) = 1 + digitsum(1) = 10 = 1 + 1 = 2
n(3) = 10 + digitsum(10) = 10 + 1 = 11 = 2 + 1 = 3
n(4) = 11 + digitsum(11) = 11 + 1+1 = 101 = 3 + 2 = 5
n(5) = 101 + digitsum(101) = 101 + 1+0+1 = 111 = 5 + 2 = 7
n(6) = 111 + digitsum(111) = 111 + 11 = 1010 = 7 + 3 = 10
n(7) = 1010 + digitsum(1010) = 1010 + 10 = 1100 = 10 + 2 = 12
n(8) = 1100 + digitsum(1100) = 1100 + 10 = 1110 = 12 + 2 = 14

1, 2, 3, 5, 7, 10, 12, 14, 17, 19, 22, 25, 28, 31, 36, 38, 41, 44, 47, 52, 55, 60, 64, 65, 67, 70, 73, 76, 79, 84, 87, 92, 96, 98, 101, 105, 109, 114, 118, 123, 129, 131, 134, 137, 140, 143, 148, 151, 156, 160, 162, 165, 169, 173, 178, 182, 187, 193, 196, 199, 204, 208, 211, 216, 220, 225, 229, 234, 239, 246, 252, 258, 260, 262, 265, 268, 271, 276, 279, 284, 288, 290, 293, 297, 301, 306, 310, 315, 321, 324, 327, 332, 336, 339, 344, 348, 353, 357, 362, 367, 374…

What patterns are there in these sequences? It’s easier to check when they’re represented graphically, so I converted them into patterns à la the Ulam spiral, where n is represented as a dot on a spiral of integers. This is the spiral for base 10:

Base 10

And these are the spirals for bases 2 and 3:

Base 2

Base 3

These sequences look fairly random to me: there are no obvious patterns in the jumps from n(i) to n(i+1), i.e. in the values for digitsum(n(i)). Now try the spirals for bases 9 and 33:

Base 9

Base 33

Patterns have appeared: there is some regularity in the jumps. You can see these regularities more clearly if you represent digitsum(n(i)) as a graph, with n(i) on the x axis and digitsum(n(i)) on the y axis. If the graph starts with n(i) = 1 on the lower left and proceeds left-right, left-right up the screen, it looks like this in base 10:

Base 10 (click to enlarge)

Here are bases 2 and 3:

Base 2

Base 3

The jumps seem fairly random. Now try bases 9, 13, 16, 17, 25, 33 and 49:

Base 9

Base 13

Base 16

Base 17

Base 25

Base 33

Base 49

In some bases, the formula n(i) = n(i-1) + digitsum(n(i-1)) generates mild randomness. In others, it generates strong regularity, like waves rolling ashore under a steady wind. I don’t understand why, but regularity seems to occur in bases that are one more than a power of 2 and also in some bases that are primes or squares.

Elsewhere other-posted:

• Mathematica Magistra Mundi

Reverssum

Wednesday, 26th Feb, 2014 by Krilling for Company in Base Behavior, Digit-sums, Mathematics and tagged Arithmetic, arithmetical, base 10, base 11, base 12, base 33, base 34, base 35, base 6, base 7, base 9, Base Behavior, base behaviour, base-dependent integer sequences, digit sum, digit sums, integer, integer bases, Integer Sequences, integers, math, mathematics, maths, number reversals, number sums, recreational math, recreational mathematics, recreational maths, repeating integer sequences, repeating sequences, reversed integers, reversing numbers | Leave a comment

Here’s a simple sequence. What’s the next number?

1, 2, 4, 8, 16, 68, 100, ?

The rule I’m using is this: Reverse the number, then add the sum of the digits. So 1 doubles till it becomes 16. Then 16 becomes 61 + 6 + 1 = 68. Then 68 becomes 86 + 8 + 6 = 100. Then 100 becomes 001 + 1 = 2. And the sequence falls into a loop.

Reversing the number means that small numbers can get big and big numbers can get small, but the second tendency is stronger for the first few seeds:

• 1 → 2 → 4 → 8 → 16 → 68 → 100 → 2
• 2 → 4 → 8 → 16 → 68 → 100 → 2
• 3 → 6 → 12 → 24 → 48 → 96 → 84 → 60 → 12
• 4 → 8 → 16 → 68 → 100 → 2 → 4
• 5 → 10 → 2 → 4 → 8 → 16 → 68 → 100 → 2
• 6 → 12 → 24 → 48 → 96 → 84 → 60 → 12
• 7 → 14 → 46 → 74 → 58 → 98 → 106 → 608 → 820 → 38 → 94 → 62 → 34 → 50 → 10 → 2 → 4 → 8 → 16 → 68 → 100 → 2
• 8 → 16 → 68 → 100 → 2 → 4 → 8
• 9 → 18 → 90 → 18
• 10 → 2 → 4 → 8 → 16 → 68 → 100 → 2

An 11-seed is a little more interesting:

11 → 13 → 35 → 61 → 23 → 37 → 83 → 49 → 107 → 709 → 923 → 343 → 353 → 364 → 476 → 691 → 212 → 217 → 722 → 238 → 845 → 565 → 581 → 199 → 1010 → 103 → 305 → 511 → 122 → 226 → 632 → 247 → 755 → 574 → 491 → 208 → 812 → 229 → 935 → 556 → 671 → 190 → 101 → 103 (11 leads to an 18-loop from 103 at step 26; total steps = 44)

Now try some higher bases:

• 1 → 2 → 4 → 8 → 15 → 57 → 86 → 80 → 15 (base=11)
• 1 → 2 → 4 → 8 → 14 → 46 → 72 → 34 → 4A → B6 → 84 → 58 → 96 → 80 → 14 (base=12)
• 1 → 2 → 4 → 8 → 13 → 35 → 5B → C8 → A6 → 80 → 13 (base=13)
• 1 → 2 → 4 → 8 → 12 → 24 → 48 → 92 → 36 → 6C → DA → C8 → A4 → 5A → B6 → 80 → 12 (base=14)
• 1 → 2 → 4 → 8 → 11 → 13 → 35 → 5B → C6 → 80 → 11 (base=15)
• 1 → 2 → 4 → 8 → 10 → 2 (base=16)

Does the 1-seed always create a short sequence? No, it gets pretty long in base-19 and base-20:

• 1 → 2 → 4 → 8 → [16] → 1D → DF → [17]3 → 4[18] → 107 → 709 → 914 → 424 → 42E → E35 → 54[17] → [17]5C → C7D → D96 → 6B3 → 3C7 → 7D6 → 6EE → E[16]2 → 2[18]8 → 90B → B1A → A2E → E3[17] → [17]5A → A7B → B90 → AC→ DD → F1 → 2C → C[16] → [18]2 → 40 → 8 (base=19)
• 1 → 2 → 4 → 8 → [16] → 1C → CE → F[18] → 108 → 80A → A16 → 627 → 731 → 13[18] → [18]43 → 363 → 36F → F77 → 794 → 4A7 → 7B5 → 5CA → ADC → CF5 → 5[17]4 → 4[18]B → B[19][17] → [18]1[18] → [18]3F → F5E → E79 → 994 → 4AB → BB9 → 9D2 → 2ED → DFB → B[17]C → C[19]B → C1E → E2[19] → [19]49 → 96B → B7F → F94 → 4B3 → 3C2 → 2D0 → D[17] → [19]3 → 51 → 1B → BD → EF → [17]3 → 4[17] → [18]5 → 71 → 1F → F[17] → [19]7 → 95 → 63 → 3F → [16]1 → 2D → D[17] (base=20)

Then it settles down again:

• 1 → 2 → 4 → 8 → [16] → 1B → BD → EE → [16]0 → 1B (base=21)
• 1 → 2 → 4 → 8 → [16] → 1A → AC → DA → BE → FE → [16]0 → 1A (base=22)
• 1 → 2 → 4 → 8 → [16] → 19 → 9B → C6 → 77 → 7[21] → [22]C → EA → BF → [16]E → [16]0 → 19 (base=23)

Base-33 is also short:

1 → 2 → 4 → 8 → [16] → [32] → 1[31] → [32]0 → 1[31] (base=33)

And so is base-35:

1 → 2 → 4 → 8 → [16] → [32] → 1[29] → [29][31] → [33][19] → [21]F → [16][22] → [23][19] → [20][30] → [32]0 → 1[29] (base=35)

So what about base-34?

1 → 2 → 4 → 8 → [16] → [32] → 1[30] → [30][32] → 10[24] → [24]0[26] → [26]26 → 63[26] → [26]47 → 75[29] → [29]6E → E8A → A9C → CA7 → 7B7 → 7B[32] → [32]C[23] → [23]E[31] → [31][16][23] → [23][18][33] → [33][20][29] → [29][23]D → D[25][26] → [26][27]9 → 9[29][20] → [20][30][33] → [33][33]1 → 21[32] → [32]23 → 341 → 14B → B4[17] → [17]59 → 96E → E74 → 485 → 58[21] → [21]95 → 5A[22] → [22]B8 → 8C[29] → [29]D[23] → [23]F[26] → [26][17][19] → [19][19][20] → [20][21]9 → 9[23]2 → 2[24]9 → 9[25]3 → 3[26]C → C[27]A → A[28][27] → [27][30]7 → 7[32][23] → [24]01 → 11F → F1[18] → [18]2F → F3[19] → [19]4[18] → [18]5[26] → [26]6[33] → [33]8[23] → [23]A[29] → [29]C[17] → [17]E[19] → [19]F[33] → [33][17][18] → [18][19][33] → [33][21][20] → [20][24]5 → 5[26]1 → 1[27]3 → 3[27][32] → [32][28][31] → [31][31][21] → [22]0C → C1[22] → [22]2D → D3[25] → [25]4[20] → [20]66 → 67[18] → [18]83 → 39D → D9[28] → [28]A[29] → [29]C[27] → [27]E[29] → [29][16][29] → [29][19]1 → 1[21]A → A[21][33] → [33][23]6 → 6[25][27] → [27][26][30] → [30][29]8 → 8[31][29] → [29][33]8 → 91[31] → [31]2[16] → [16]4C → C5E → E69 → 979 → 980 → 8[26] → [27]8 → 9[28] → [29]C → E2 → 2[30] → [31]0 → 1[28] → [28][30] → [32][18] → [20]E → F[20] → [21][16] → [17][24] → [25][24] → [26]6 → 7[24] → [25]4 → 5[20] → [20][30] → [32]2 → 3[32] → [33]4 → 62 → 2E → E[18] → [19]C → D[16] → [17]8 → 98 → 8[26] (1 leads to a 30-loop from 8[26] / 298 in base-34 at step 111; total steps = 141)

An alternative rule is to add the digit-sum first and then reverse the result. Now 8 becomes 8 + 8 = 16 and 16 becomes 61. Then 61 becomes 61 + 6 + 1 = 68 and 68 becomes 86. Then 86 becomes 86 + 8 + 6 = 100 and 100 becomes 001 = 1:

• 1 → 2 → 4 → 8 → 61 → 86 → 1
• 2 → 4 → 8 → 61 → 86 → 1 → 2
• 3 → 6 → 21 → 42 → 84 → 69 → 48 → 6
• 4 → 8 → 61 → 86 → 1 → 2 → 4
• 5 → 1 → 2 → 4 → 8 → 62 → 7 → 48 → 6 → 27 → 63 → 27
• 6 → 21 → 42 → 84 → 69 → 48 → 6
• 7 → 41 → 64 → 47 → 85 → 89 → 601 → 806 → 28 → 83 → 49 → 26 → 43 → 5 → 6 → 27 → 63 → 27
• 8 → 61 → 86 → 1 → 2 → 4 → 8
• 9 → 81 → 9
• 10 → 11 → 31 → 53 → 16 → 32 → 73 → 38 → 94 → 701 → 907 → 329 → 343 → 353 → 463 → 674 → 196 → 212 → 712 → 227 → 832 → 548 → 565 → 185 → 991 → 101 → 301 → 503 → 115 → 221 → 622 → 236 → 742 → 557 → 475 → 194→ 802 → 218 → 922 → 539 → 655 → 176 → 91 → 102 → 501 → 705 → 717 → 237 → 942 → 759 → 87 → 208 → 812 → 328 → 143 → 151 → 851 → 568 → 785 → 508 → 125 → 331 → 833 → 748 → 767 → 787 → 908 → 529 → 545 → 955 → 479 → 994 → 6102 → 1116 → 5211 → 225 → 432 → 144 → 351 → 63 → 27 → 63

Block and Goal

Thursday, 13th Feb, 2014 by Krilling for Company in Base Behavior, Mathematics and tagged 123456789, 987654321, Arithmetic, base 10, base 11, base 12, base 13, base 17, base 9, base-dependent integer sequences, block of integers, even numbers, formula for 100, integer bases, Integer Sequences, integers, math, mathematics, maths, number sums, odd and even, odd numbers, parity, plus and minus, powers of n, recreational math, recreational mathematics, recreational maths, sum of integers | Leave a comment

123456789. How many ways are there to insert + and – between the numbers and create a formula for 100? With pen and ink it takes a long time to answer. With programming, the answer will flash up in an instant:

01. 1 + 2 + 3 - 4 + 5 + 6 + 78 + 9 = 100
02. 1 + 2 + 34 - 5 + 67 - 8 + 9 = 100
03. 1 + 23 - 4 + 5 + 6 + 78 - 9 = 100
04. 1 + 23 - 4 + 56 + 7 + 8 + 9 = 100
05. 12 - 3 - 4 + 5 - 6 + 7 + 89 = 100
06. 12 + 3 + 4 + 5 - 6 - 7 + 89 = 100
07. 12 + 3 - 4 + 5 + 67 + 8 + 9 = 100
08. 123 - 4 - 5 - 6 - 7 + 8 - 9 = 100
09. 123 + 4 - 5 + 67 - 89 = 100
10. 123 + 45 - 67 + 8 - 9 = 100
11. 123 - 45 - 67 + 89 = 100

And the beauty of programming is that you can easily generalize the problem to other bases. In base b, how many ways are there to insert + and – in the block [12345…b-1] to create a formula for b^2? When b = 10, the answer is 11. When b = 11, it’s 42. Here are two of those formulae in base-11:

123 - 45 + 6 + 7 - 8 + 9 + A = 100_[b=11]
146 - 49 + 6 + 7 - 8 + 9 + 10 = 121

123 + 45 + 6 + 7 - 89 + A = 100_[b=11]
146 + 49 + 6 + 7 - 97 + 10 = 121

When b = 12, it’s 51. Here are two of the formulae:

123 + 4 + 5 + 67 - 8 - 9A + B = 100_[b=12]
171 + 4 + 5 + 79 - 8 - 118 + 11 = 144

123 + 4 + 56 + 7 - 89 - A + B = 100_[b=12]
171 + 4 + 66 + 7 - 105 - 10 + 11 = 144

So that’s 11 formulae in base-10, 42 in base-11 and 51 in base-12. So what about base-13? The answer may be surprising: in base-13, there are no +/- formulae for 13^2 = 169 using the numbers 1 to 12. Nor are there any formulae in base-9 for 9^2 = 81 using the numbers 1 to 8. If you reverse the block, 987654321, the same thing happens. Base-10 has 15 formulae, base-11 has 54 and base-12 has 42. Here are some examples:

9 - 8 + 7 + 65 - 4 + 32 - 1 = 100
98 - 76 + 54 + 3 + 21 = 100

A9 + 87 - 65 + 4 - 3 - 21 = 100_[b=11]
119 + 95 - 71 + 4 - 3 - 23 = 121

BA - 98 + 76 - 5 - 4 + 32 - 1 = 100_[b=12]
142 - 116 + 90 - 5 - 4 + 38 - 1 = 144

But base-9 and base-13 again have no formulae. What’s going on? Is it a coincidence that 9 and 13 are each one more than a multiple of 4? No. Base-17 also has no formulae for b^2 = 13^2 = 169. Here is the list of formulae for bases-7 thru 17:

1, 2, 0, 11, 42, 51, 0, 292, 1344, 1571, 0 (block = 12345...)
3, 2, 0, 15, 54, 42, 0, 317, 1430, 1499, 0 (block = ...54321)

To understand what’s going on, consider any sequence of consecutive integers starting at 1. The number of odd integers in the sequence must always be greater than or equal to the number of even integers:

1, 2 (1 odd : 1 even)
1, 2, 3 (2 odds : 1 even)
1, 2, 3, 4 (2 : 2)
1, 2, 3, 4, 5 (3 : 2)
1, 2, 3, 4, 5, 6 (3 : 3)
1, 2, 3, 4, 5, 6, 7 (4 : 3)
1, 2, 3, 4, 5, 6, 7, 8 (4 : 4)

The odd numbers in a sequence determine the parity of the sum, that is, whether it is odd or even. For example:

1 + 2 = 3 (1 odd number)
1 + 2 + 3 = 6 (2 odd numbers)
1 + 2 + 3 + 4 = 10 (2 odd numbers)
1 + 2 + 3 + 4 + 5 = 15 (3 odd numbers)
1 + 2 + 3 + 4 + 5 + 6 = 21 (3 odd numbers)
1 + 2 + 3 + 4 + 5 + 6 + 7 = 28 (4 odd numbers)

If there is an even number of odd numbers, the sum will be even; if there is an odd number, the sum will be odd. Consider sequences that end in a multiple of 4:

1, 2, 3, 4 → 2 odds : 2 evens
1, 2, 3, 4, 5, 6, 7, 8 → 4 : 4
1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12 → 6 : 6

Such sequences always contain an even number of odd numbers. Now, consider these formulae in base-10:

1. 12 + 3 + 4 + 56 + 7 + 8 + 9 = 99
2. 123 - 45 - 67 + 89 = 100
3. 123 + 4 + 56 + 7 - 89 = 101

They can be re-written like this:

1. 1×10^1 + 2×10^0 + 3×10^0 + 4×10^0 + 5×10^1 + 6×10^0 + 7×10^0 + 8×10^0 + 9×10^0 = 99

2. 1×10^2 + 2×10^1 + 3×10^0 – 4×10^1 – 5×10^0 – 6×10^1 – 7×10^0 + 8×10^1 + 9×10^0 = 100

3. 1×10^2 + 2×10^1 + 3×10^0 + 4×10^0 + 5×10^1 + 6×10^1 + 7×10^0 – 8×10^1 – 9×10^0 = 101

In general, the base-10 formulae will take this form:

1×10^a +/- 2×10^b +/- 3×10^c +/– 4×10^d +/– 5×10^e +/– 6×10^f +/– 7×10^g +/– 8×10^h +/– 9×10^i = 100

It’s important to note that the exponent of 10, or the power to which it is raised, determines whether an odd number remains odd or becomes even. For example, 3×10^0 = 3×1 = 3, whereas 3×10^1 = 3×10 = 30 and 3×10^2 = 3×100 = 300. Therefore the number of odd numbers in a base-10 formula can vary and so can the parity of the sum. Now consider base-9. When you’re trying to find a block-formula for 9^2 = 81, the formula will have to take this form:

1×9^a +/- 2×9^b +/- 3×9^c +/- 4×9^d +/- 5×9^e +/- 6×9^f +/- 7×9^g +/- 8×9^h = 81

But no such formula exists for 81 (with standard exponents). It’s now possible to see why this is so. Unlike base-10, the odd numbers in the formula will remain odd what the power of 9. For example, 3×9^0 = 3×1 = 3, 3×9^1 = 3×9 = 27 and 3×9^2 = 3×81 = 243. Therefore base-9 formulae will always contain four odd numbers and will always produce an even number. Odd numbers in base-2 always end in 1, even numbers always end in 0. Therefore, to determine the parity of a sum of integers, convert the integers to base-2, discard all but the final digit of each integer, then sum the 1s. In a base-9 formula, these are the four possible results:

1 + 1 + 1 + 1 = 4
1 + 1 + 1 - 1 = 2
1 + 1 - 1 - 1 = 0
1 - 1 - 1 - 1 = -2

The sum represents the parity of the answer, which is always even. Similar reasoning applies to base-13, base-17 and all other base-[b=4n+1].

Persist List

Friday, 31st Jan, 2014 by Krilling for Company in Base Behavior, Mathematics, Narcissistic numbers and tagged Arithmetic, arithmetical, base 10, base 108, base 11, base 12, base 27, base 9, Base Behavior, base behaviour, integer, integers, math, mathematics, maths, multiplicative persistence, narcissistic multiplicative persistence sums, narcissistic number, narcissistic numbers, recreational math, recreational mathematics, recreational maths, sum of integers, sum of products | 1 Comment

Multiplicative persistence is a complex term but a simple concept. Take a number, multiply its digits, repeat. Sooner or later the result is a single digit:

25 → 2 x 5 = 10 → 1 x 0 = 0 (mp=2)
39 → 3 x 9 = 27 → 2 x 7 = 14 → 1 x 4 = 4 (mp=3)

So 25 has a multiplicative persistence of 2 and 39 a multiplicative persistence of 3. Each is the smallest number with that m.p. in base-10. Further records are set by these numbers:

77 → 49 → 36 → 18 → 8 (mp=4)
679 → 378 → 168 → 48 → 32 → 6 (mp=5)
6788 → 2688 → 768 → 336 → 54 → 20 → 0 (mp=6)
68889 → 27648 → 2688 → 768 → 336 → 54 → 20 → 0 (mp=7)
2677889 → 338688 → 27648 → 2688 → 768 → 336 → 54 → 20 → 0 (mp=8)
26888999 → 4478976 → 338688 → 27648 → 2688 → 768 → 336 → 54 → 20 → 0 (mp=9)
3778888999 → 438939648 → 4478976 → 338688 → 27648 → 2688 → 768 → 336 → 54 → 20 → 0 (mp=10)

Now here’s base-9:

25_[b=9] → 11 → 1 (mp=2)
38_[b=9] → 26 → 13 → 3 (mp=3)
57_[b=9] → 38 → 26 → 13 → 3 (mp=4)
477_[b=9] → 237 → 46 → 26 → 13 → 3 (mp=5)
45788_[b=9] → 13255 → 176 → 46 → 26 → 13 → 3 (mp=6)
2577777_[b=9] → 275484 → 13255 → 176 → 46 → 26 → 13 → 3 (mp=7)

And base-11:

26_[b=11] → 11 → 1 (mp=2)
3A_[b=11] → 28 → 15 → 5 (mp=3)
69_[b=11] → 4A → 37 → 1A → A (=10_b=10) (mp=4)
269_[b=11] → 99 → 74 → 26 → 11 → 1 (mp=5)
3579_[b=11] → 78A → 46A → 1A9 → 82 → 15 → 5 (mp=6)
26778_[b=11] → 3597 → 78A → 46A → 1A9 → 82 → 15 → 5 (mp=7)
47788A_[b=11] → 86277 → 3597 → 78A → 46A → 1A9 → 82 → 15 → 5 (mp=8)
67899AAA_[b=11] → 143A9869 → 299596 → 2A954 → 2783 → 286 → 88 → 59 → 41 → 4 (mp=9)
77777889999_[b=11] → 2AA174996A → 143A9869 → 299596 → 2A954 → 2783 → 286 → 88 → 59 → 41 → 4 (mp=10)

I was also interested in the narcissism of multiplicative persistence. That is, are any numbers equal to the sum of the numbers created while calculating their multiplicative persistence? Yes:

86 = (8 x 6 = 48) + (4 x 8 = 32) + (3 x 2 = 6)

I haven’t found any more in base-10 (apart from the trivial 0 to 9) and can’t prove that this is the only one. Base-9 offers this:

78_[b=9] = 62 + 13 + 3

I can’t find any at all in base-11, but here are base-12 and base-27:

57_[b=12] = 2B + 1A + A
A8_[b=12] = 68 + 40 + 0

4[23]_[b=27] = 3B + 16 + 6
7[24]_[b=27] = 66 + 19 + 9
A[18]_[b=27] = 6[18] + 40 + 0
[26][24]_[b=27] = [23]3 + 2F + 13 + 3
[26][23][26]_[b=27] = [21]8[23] + 583 + 4C + 1[21] + [21]

But the richest base I’ve found so far is base-108, with fourteen narcissistic multiplicative-persistence sums:

4[92]_[b=108] = 3[44] + 1[24] + [24]
5[63]_[b=108] = 2[99] + 1[90] + [90]
7[96]_[b=108] = 6[24] + 1[36] + [36]
A[72]_[b=108] = 6[72] + 40 + 0
[19][81]_[b=108] = E[27] + 3[54] + 1[54] + [54]
[26][96]_[b=108] = [23]C + 2[60] + 1C + C
[35][81]_[b=108] = [26][27] + 6[54] + 30 + 0
[37][55]_[b=108] = [18][91] + F[18] + 2[54] + 10 + 0
[73][60]_[b=108] = [40][60] + [22][24] + 4[96] + 3[60] + 1[72] + [72]
[107][66]_[b=108] = [65][42] + [25][30] + 6[102] + 5[72] + 3[36] + 10 + 0
[71][84]_[b=108] = [55][24] + C[24] + 2[72] + 1[36] + [36]
[107][99]_[b=108] = [98]9 + 8[18] + 1[36] + [36]
5[92][96]_[b=108] = 3[84][96] + 280 + 0
8[107][100]_[b=108] = 7[36][64] + 1[41][36] + D[72] + 8[72] + 5[36] + 1[72] + [72]

Update (10/ii/14): The best now is base-180 with eighteen multiplicative-persistence sums.

5[105]_[b=180] = 2[165] + 1[150] + [150]
7[118]_[b=180] = 4[106] + 2[64] + [128]
7[160]_[b=180] = 6[40] + 1[60] + [60]
8[108]_[b=180] = 4[144] + 3[36] + [108]
A[120]_[b=180] = 6[120] + 40 + 0 (s=5)
[19][135]_[b=180] = E[45] + 3[90] + 1[90] + [90]
[21][108]_[b=180] = C[108] + 7[36] + 1[72] + [72]
[26][160]_[b=180] = [23][20] + 2[100] + 1[20] + [20]
[31][98]_[b=180] = [16][158] + E8 + [112]
[35][135]_[b=180] = [26][45] + 6[90] + 30 + 0 (s=10)
[44][96]_[b=180] = [23][84] + A[132] + 7[60] + 2[60] + [120]
[71][140]_[b=180] = [55][40] + C[40] + 2[120] + 1[60] + [60]
[73][100]_[b=180] = [40][100] + [22][40] + 4[160] + 3[100] + 1[120] + [120]
[107][110]_[b=180] = [65][70] + [25][50] + 6[170] + 5[120] + 3[60] + 10 + 0
[107][165]_[b=180] = [98]F + 8[30] + 1[60] + [60] (s=15)
[172][132]_[b=180] = [126][24] + [16][144] + C[144] + 9[108] + 5[72] + 20 + 0
5[173][145]_[b=180] = 3[156][145] + 2[17]0 + 0
E[170][120]_[b=180] = 8[146][120] + 4[58][120] + [154][120] + [102][120] + [68]0 + 0

Overlord In Terms of Core Issues Around Maximal Engagement with Key Notions of the Über-Feral

მეფე (2) • მსოფლიოს (3) • მათემატიკა (5) •

Tag Archives: base 9