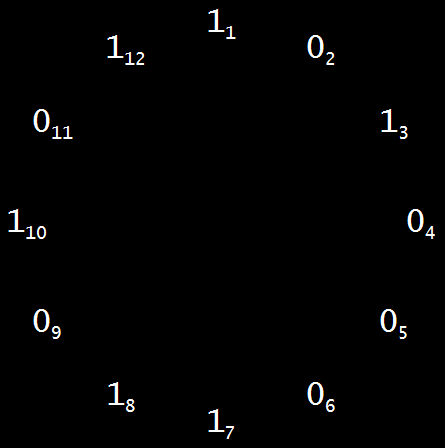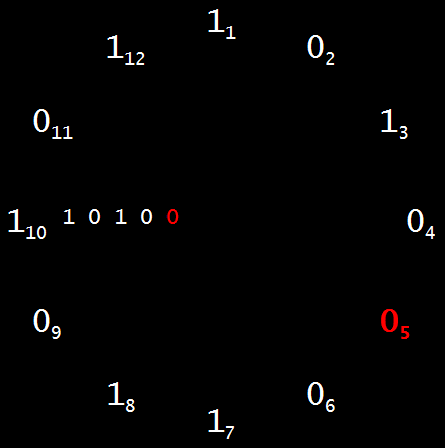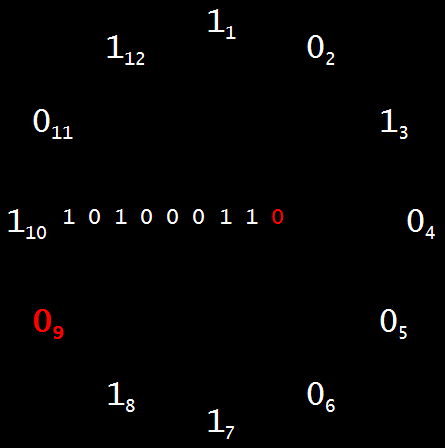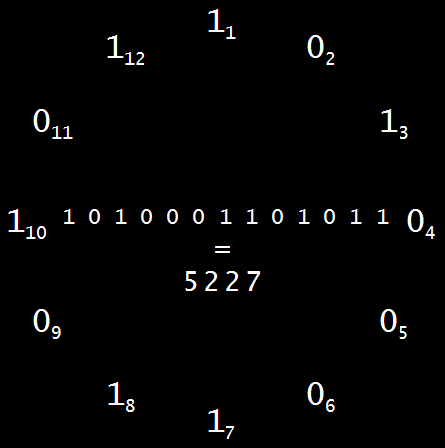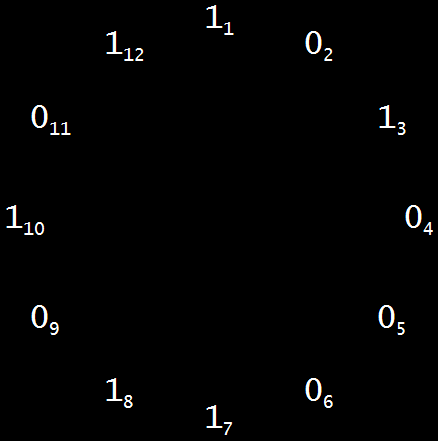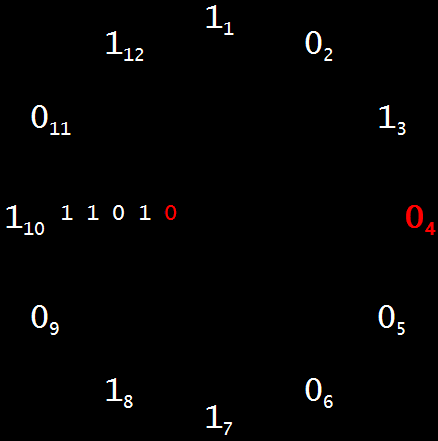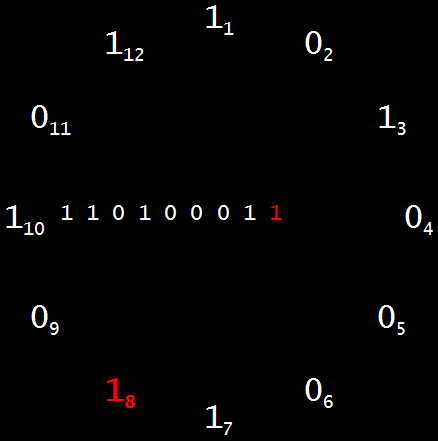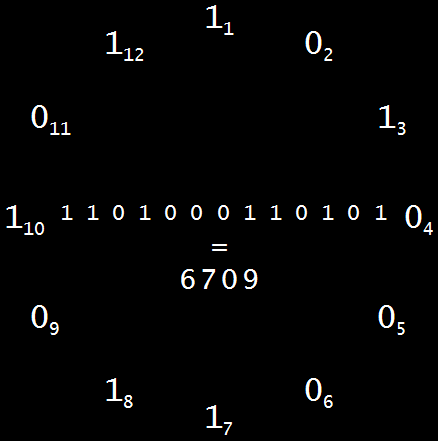Tag Archives: binary

Spijit

by in Base Behavior, Mathematics, Ulam Spirals and tagged , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , | Leave a comment

The only two digits found in all standard bases are 1 and 0. But they behave quite differently. Suppose you take the integers 1 to 100 and compare the number of 1s and 0s in the representation of each integer, n, in bases 2 to n-1. For example, 10 would look like this:

1010 in base 2
101 in base 3
22 in base 4
20 in base 5
14 in base 6
13 in base 7
12 in base 8
11 in base 9

So there are nine 1s and four 0s. If you check 1 to 100 using this all-base function, the count of 1s goes like this:

1, 1, 2, 3, 5, 5, 8, 5, 9, 9, 11, 10, 15, 12, 14, 13, 15, 12, 17, 14, 20, 19, 20, 15, 23, 19, 22, 22, 25, 24, 31, 21, 25, 24, 24, 27, 33, 27, 31, 29, 34, 29, 36, 30, 34, 35, 34, 30, 40, 33, 36, 35, 38, 34, 42, 37, 43, 40, 41, 37, 48, 39, 42, 42, 44, 43, 48, 43, 47, 46, 51, 42, 53, 44, 48, 50, 51, 50, 55, 48, 59, 55, 55, 54, 64, 57, 57, 55, 60, 57, 68, 60, 64, 63, 64, 59, 68, 58, 61, 63.

And the count of 0s goes like this:

0, 1, 0, 2, 1, 2, 0, 4, 4, 4, 2, 5, 1, 2, 2, 7, 4, 8, 4, 7, 4, 3, 1, 8, 4, 4, 6, 8, 4, 7, 1, 10, 8, 7, 7, 12, 5, 6, 5, 10, 4, 8, 2, 6, 7, 4, 2, 12, 6, 9, 7, 8, 4, 11, 6, 10, 5, 4, 2, 12, 2, 3, 5, 14, 11, 13, 7, 10, 8, 11, 5, 17, 7, 8, 10, 10, 8, 10, 4, 13, 12, 10, 8, 16, 8, 7, 7, 12, 6, 14, 6, 8, 5, 4, 4, 16, 6, 10, 11, 15.

The bigger the numbers get, the bigger the discrepancies get. Sometimes the discrepancy is dramatic. For example, suppose you represented the prime 1014719 in bases 2 to 1014718. How 0s would there be? And how many 1s? There are exactly nine zeroes:

1014719 = 11110111101110111111 in base 2 = 1220112221012 in base 3 = 40B27B in base 12 = 1509CE in base 15 = 10[670] in base 1007.

But there are 507723 ones. The same procedure applied to the next integer, 1014720, yields 126 zeroes and 507713 ones. However, there is a way to see that 1s and 0s in the all-base representation are behaving in a similar way. To do this, imagine listing the individual digits of n in bases 2 to n-1 (or just base 2, if n <= 3). When the digits aren’t individual they look like this:

1 = 1 in base 2
2 = 10 in base 2
3 = 11 in base 2
4 = 100 in base 2; 11 in base 3
5 = 101 in base 2; 12 in base 3; 11 in base 4
6 = 110 in base 2; 20 in base 3; 12 in base 4; 11 in base 5
7 = 111 in base 2; 21 in base 3; 13 in base 4; 12 in base 5; 11 in base 6
8 = 1000 in base 2; 22 in base 3; 20 in base 4; 13 in base 5; 12 in base 6; 11 in base 7
9 = 1001 in base 2; 100 in base 3; 21 in base 4; 14 in base 5; 13 in base 6; 12 in base 7; 11 in base 8
10 = 1010 in base 2; 101 in base 3; 22 in base 4; 20 in base 5; 14 in base 6; 13 in base 7; 12 in base 8; 11 in base 9

So the list would look like this:

1, 1, 0, 1, 1, 1, 0, 0, 1, 1, 1, 0, 1, 1, 2, 1, 1, 1, 1, 0, 2, 0, 1, 2, 1, 1, 1, 1, 1, 2, 1, 1, 3, 1, 2, 1, 1, 1, 0, 0, 0, 2, 2, 2, 0, 1, 3, 1, 2, 1, 1, 1, 0, 0, 1, 1, 0, 0, 2, 1, 1, 4, 1, 3, 1, 2, 1, 1, 1, 0, 1, 0, 1, 0, 1, 2, 2, 2, 0, 1, 4, 1, 3, 1, 2, 1, 1

Suppose that these digits are compared against the squares of a counter-clockwise spiral on a rectangular grid. If the spiral digit is equal to 1, the square is filled in; if the spijit is not equal to 1, the square is left blank. The 1-spiral looks like this:
1spiral
Now try zero. If the spijit is equal to 0, the square is filled in; if not, the square is left blank. The 0-spiral looks like this:
0spiral
And here’s an animated gif of the n-spiral for n = 0..9:
animspiral

N-route

by in Binary numbers, Digit-sums, Geometry, Mathematics and tagged , , , , , , , , , , , , , , , , , , | Leave a comment

In maths, one thing leads to another. I wondered whether, in a spiral of integers, any number was equal to the digit-sum of the numbers on the route traced by moving to the origin first horizontally, then vertically. To illustrate the procedure, here is a 9×9 integer spiral containing 81 numbers:

| 65 | 64 | 63 | 62 | 61 | 60 | 59 | 58 | 57 |
| 66 | 37 | 36 | 35 | 34 | 33 | 32 | 31 | 56 |
| 67 | 38 | 17 | 16 | 15 | 14 | 13 | 30 | 55 |
| 68 | 39 | 18 | 05 | 04 | 03 | 12 | 29 | 54 |
| 69 | 40 | 19 | 06 | 01 | 02 | 11 | 28 | 53 |
| 70 | 41 | 20 | 07 | 08 | 09 | 10 | 27 | 52 |
| 71 | 42 | 21 | 22 | 23 | 24 | 25 | 26 | 51 |
| 72 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 |
| 73 | 74 | 75 | 76 | 77 | 78 | 79 | 80 | 81 |

Take the number 21, which is three places across and up from the bottom left corner of the spiral. The route to the origin contains the numbers 21, 22, 23, 8 and 1, because first you move right two places, then up two places. And 21 is what I call a route number, because 21 = 3 + 4 + 5 + 8 + 1 = digitsum(21) + digitsum(22) + digitsum(23) + digitsum(8) + digitsum(1). Beside the trivial case of 1, there are two more route numbers in the spiral:

58 = 13 + 14 + 6 + 7 + 7 + 6 + 4 + 1 = digitsum(58) + digitsum(59) + digitsum(60) + digitsum(61) + digitsum(34) + digitsum(15) + digitsum(4) + digitsum(1).

74 = 11 + 12 + 13 + 14 + 10 + 5 + 8 + 1 = digitsum(74) + digitsum(75) + digitsum(76) + digitsum(77) + digitsum(46) + digitsum(23) + digitsum(8) + digitsum(1).

Then I wondered about other possible routes to the origin. Think of the origin as one corner of a rectangle and the number being tested as the diagonal corner. Suppose that you always move away from the starting corner, that is, you always move up or right (or up and left, and so on, depending on where the corners lie). In a x by y rectangle, how many routes are there between the diagonal corners under those conditions?

It’s an interesting question, but first I’ve looked at the simpler case of an n by n square. You can encode each route as a binary number, with 0 representing a vertical move and 1 representing a horizontal move. The problem then becomes equivalent to finding the number of distinct ways you can arrange equal numbers of 1s and 0s. If you use this method, you’ll discover that there are two routes across the 2×2 square, corresponding to the binary numbers 01 and 10:

2x2

Across the 3×3 square, there are six routes, corresponding to the binary numbers 0011, 0101, 0110, 1001, 1010 and 1100:

3x3

Across the 4×4 square, there are twenty routes:
4x4

(Please open in new window if it fails to animate)

(Please open in new window if it fails to animate)

Across the 5×5 square, there are 70 routes:

5x5

(Please open in new window etc)

(Please open in new window etc)

Across the 6×6 and 7×7 squares, there are 252 and 924 routes:

6x6

7x7

After that, the routes quickly increase in number. This is the list for n = 1 to 14:

1, 2, 6, 20, 70, 252, 924, 3432, 12870, 48620, 184756, 705432, 2704156, 10400600… (see A000984 at the Online Encyclopedia of Integer Sequences)

After that you can vary the conditions. What if you can move not just vertically and horizontally, but diagonally, i.e. vertically and horizontally at the same time? Now you can encode the route with a ternary number, or number in base 3, with 0 representing a vertical move, 1 a horizontal move and 2 a diagonal move. As before, there is one route across a 1×1 square, but there are three across a 2×2, corresponding to the ternary numbers 01, 2 and 10:

3x3t

There are 13 routes across a 3×3 square, corresponding to the ternary numbers 0011, 201, 021, 22, 0101, 210, 1001, 120, 012, 102, 0110, 1010, 1100:

4x4t

And what about cubes, hypercubes and higher?

He Say, He Sigh, He Sow #20

by in Binary numbers, Geometry, π, Mathematics, Pi, Quotations and tagged , , , , , , , , , , , , , , , , , , , , , | 6 Comments

“In 1997, Fabrice Bellard announced that the trillionth digit of π, in binary notation, is 1.” — Ian Stewart, The Great Mathematical Problems (2013).

Prime Climb Time

by in Base Behavior, Binary numbers, Digit-sums, Mathematics, Prime numbers and tagged , , , , , , , , , , , , , , , , , , , , , , | Leave a comment

The third prime is equal to the sum of the first and second primes: 2 + 3 = 5. After that, for obvious reasons, the prime-sum climbs much more rapidly than the primes themselves:

2, 3, 05, 07, 11, 13, 17, 19, 023, 029...
2, 5, 10, 17, 28, 41, 58, 77, 100, 129...

But what if you use digit-sum(p1..pn), i.e., the sum of the digits of the primes from the first to the nth? For example, the digit-sum(p1..p5) = 2 + 3 + 5 + 7 + 1+1 = 19, whereas the sum(p1..p5) = 2 + 3 + 5 + 7 + 11 = 28. Using the digit-sums of the primes, the comparison now looks like this:

2, 3, 05, 07, 11, 13, 17, 19, 23, 29...
2, 5, 10, 17, 19, 23, 31, 41, 46, 57...

The sum climbs more slowly, but still too fast. So what about a different base? In base-2, the digit-sum(p1..p3) = (1+0) + (1+1) + (1+0+1) = 1 + 2 + 2 = 5. The comparison looks like this:

2, 3, 05, 07, 11, 13, 17, 19, 23, 29...
1, 3, 05, 08, 11, 14, 16, 19, 23, 27...

For primes 3, 5, 11, 19, and 23, p = digit-sum(primes <= p) in base-2. But the cumulative digit-sum soon begins to climb too slowly:

2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97, 101, 103, 107, 109, 113, 127, 131, 137, 139, 149, 151, 157, 163, 167, 173, 179, 181, 191, 193, 197, 199, 211, 223, 227, 229, 233, 239, 241, 251, 257, 263, 269, 271...

1, 3, 5, 8, 11, 14, 16, 19, 23, 27, 32, 35, 38, 42, 47, 51, 56, 61, 64, 68, 71, 76, 80, 84, 87, 091, 096, 101, 106, 110, 117, 120, 123, 127, 131, 136, 141, 145, 150, 155, 160, 165, 172, 175, 179, 184, 189, 196, 201, 206, 211, 218, 223, 230, 232, 236, 240, 245...

So what about base-3?

2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59...
2, 3, 6, 9, 12, 15, 20, 23, 28, 31, 34, 37, 42, 47, 52, 59, 64...

In base-3, for p = 2, 3 and 37, p = digit-sum(primes <= p), while for p = 23, 31, 47 and 59, p = digit-sum(primes < p), like this:

2 = 2.
3 = 2 + (1+0).
37 = 2 + (1+0) + (1+2) + (2+1) + (1+0+2) + (1+1+1) + (1+2+2) + (2+0+1) + (2+1+2) + (1+0+0+2) + (1+0+1+1) + (1+1+0+1) = 2 + 1 + 3 + 3 + 3 + 3 + 5 + 3 + 5 + 3 + 3 + 3.

23 = 2 + (1+0) + (1+2) + (2+1) + (1+0+2) + (1+1+1) + (1+2+2) + (2+0+1) = 2 + 1 + 3 + 3 + 3 + 3 + 5 + 3.
31 = 2 + (1+0) + (1+2) + (2+1) + (1+0+2) + (1+1+1) + (1+2+2) + (2+0+1) + (2+1+2) + (1+0+0+2) = 2 + 1 + 3 + 3 + 3 + 3 + 5 + 3 + 5 + 3.
47 = 2 + (1+0) + (1+2) + (2+1) + (1+0+2) + (1+1+1) + (1+2+2) + (2+0+1) + (2+1+2) + (1+0+0+2) + (1+0+1+1) + (1+1+0+1) + (1+1+1+2) + (1+1+2+1) = 2 + 1 + 3 + 3 + 3 + 3 + 5 + 3 + 5 + 3 + 3 + 3 + 5 + 5.
59 = 2 + (1+0) + (1+2) + (2+1) + (1+0+2) + (1+1+1) + (1+2+2) + (2+0+1) + (2+1+2) + (1+0+0+2) + (1+0+1+1) + (1+1+0+1) + (1+1+1+2) + (1+1+2+1) + (1+2+0+2) + (1+2+2+2) = 2 + 1 + 3 + 3 + 3 + 3 + 5 + 3 + 5 + 3 + 3 + 3 + 5 + 5 + 5 + 7.

This carries on for a long time. For these primes, p = digit-sum(primes < p):

23, 31, 47, 59, 695689, 698471, 883517, 992609, 992737, 993037, 1314239, 1324361, 1324571, 1326511, 1327289, 1766291, 3174029

And for these primes, p = digit-sum(primes <= p):

3, 37, 695663, 695881, 1308731, 1308757, 1313153, 1314301, 1326097, 1766227, 3204779, 14328191

Now try the cumulative digit-sum in base-4:

2, 3, 5, 07, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59...
2, 5, 7, 11, 16, 20, 22, 26, 31, 36, 43, 47, 52, 59, 67, 72, 80...

The sum of digits climbs too fast. Base-3 is the Goldilocks base, climbing neither too slowly, like base-2, nor too fast, like all bases greater than 3.

Clock around the Rock

by in Art, Binary numbers, Mathematics, Palindromic numbers, Prime numbers and tagged , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , | Leave a comment

If you like minimalism, you should like binary. There is unsurpassable simplicity and elegance in the idea that any number can be reduced to a series of 1’s and 0’s. It’s unsurpassable because you can’t get any simpler: unless you use finger-counting, two symbols are the minimum possible. But with those two – a stark 1 and 0, true and false, yin and yang, sun and moon, black and white – you can conquer any number you please. 2 = 10[2]. 5 = 101. 100 = 1100100. 666 = 1010011010. 2013 = 11111011101. 9^9 = 387420489 = 10111000101111001000101001001. You can also perform any mathematics you please, from counting sheep to modelling the evolution of the universe.

Yin and Yang symbol

1 + 0 = ∞

But one disadvantage of binary, from the human point of view, is that numbers get long quickly: every doubling in size adds an extra digit. You can overcome that disadvantage using octal or hexadecimal, which compress blocks of binary into single digits, but those number systems need more symbols: eight and sixteen, as their names suggest. There’s an elegance there too, but binary goes masked, hiding its minimalist appeal beneath apparent complexity. It doesn’t need to wear a mask for computers, but human beings can appreciate bare binary too, even with our weak memories and easily tiring nervous systems. I especially like minimalist binary when it’s put to work on those most maximalist of numbers: the primes. You can compare integers, or whole numbers, to minerals. Some are like mica or shale, breaking readily into smaller parts, but primes are like granite or some other ultra-hard, resistant rock. In other words, some integers are easy to divide by other integers and some, like the primes, are not. Compare 256 with 257. 256 = 2^8, so it’s divisible by 128, 64, 32, 16, 8, 4, 2 and 1. 257 is a prime, so it’s divisible by nothing but itself and 1. Powers of two are easy to calculate and, in binary, very easy to represent:

2^0 = 1 = 1
2^1 = 2 = 10[2]
2^2 = 4 = 100
2^3 = 8 = 1000
2^4 = 16 = 10000
2^5 = 32 = 100000
2^6 = 64 = 1000000
2^7 = 128 = 10000000
2^8 = 256 = 100000000

Primes are the opposite: hard to calculate and usually hard to represent, whatever the base:

02 = 000010[2]
03 = 000011
05 = 000101
07 = 000111
11 = 001011
13 = 001101
17 = 010001
19 = 010011
23 = 010111
29 = 011101
31 = 011111
37 = 100101
41 = 101001
43 = 101011

Maximalist numbers, minimalist base: it’s a potent combination. But “brimes”, or binary primes, nearly all have one thing in common. Apart from 2, a special case, each brime must begin and end with 1. For the digits in-between, the God of Mathematics seems to be tossing a coin, putting 1 for heads, 0 for tails. But sometimes the coin will come up all heads or all tails: 127 = 1111111[2] and 257 = 100000001, for example. Brimes like that have a stark simplicity amid the jumble of 83 = 1010011[2], 113 = 1110001, 239 = 11101111, 251 = 11111011, 277 = 100010101, and so on. Brimes like 127 and 257 are also palindromes, or the same reading in both directions. But less simple brimes can be palindromes too:

73 = 1001001
107 = 1101011
313 = 100111001
443 = 110111011
1193 = 10010101001
1453 = 10110101101
1571 = 11000100011
1619 = 11001010011
1787 = 11011111011
1831 = 11100100111
1879 = 11101010111

But, whether they’re palindromes or not, all brimes except 2 begin and end with 1, so they can be represented as rings, like this:

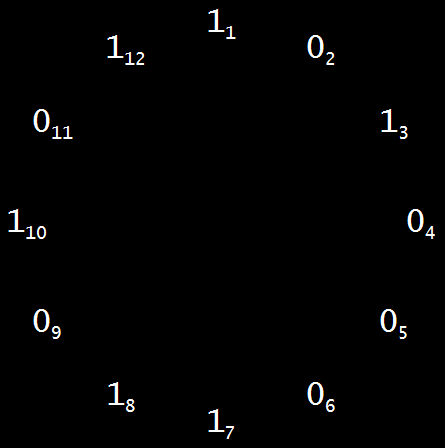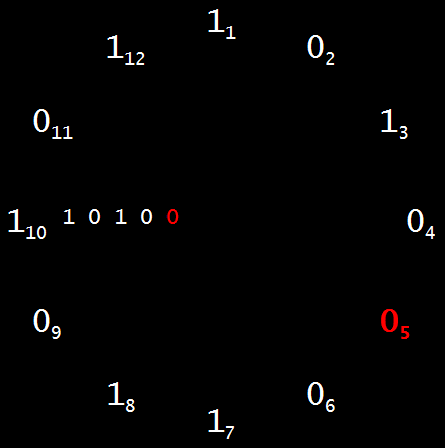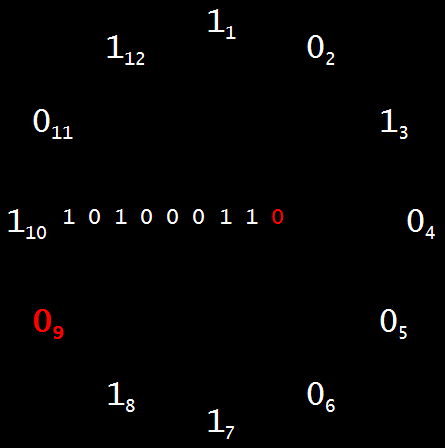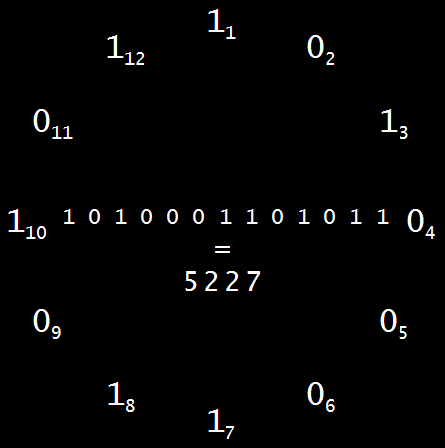
Ouroboros5227

Those twelve bits, or binary digits, actually represent the thirteen bits of 5227 = 1,010,001,101,011. Start at twelve o’clock (digit 1 of the prime) and count clockwise, adding 1’s and 0’s till you reach 12 o’clock again and add the final 1. Then you’ve clocked around the rock and created the granite of 5227, which can’t be divided by any integers but itself and 1. Another way to see the brime-ring is as an Ouroboros (pronounced “or-ROB-or-us”), a serpent or dragon biting its own tail, like this:

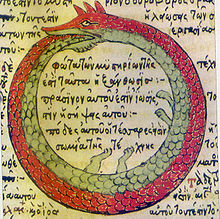
Alchemical Ouroboros

Alchemical Ouroboros (1478)

Dragon Ouroboros

Another alchemical Ouroboros (1599)

But you don’t have to start clocking around the rock at midday or midnight. Take the Ouroboprime of 5227 and start at eleven o’clock (digit 12 of the prime), adding 1’s and 0’s as you move clockwise. When you’ve clocked around the rock, you’ll have created the granite of 6709, another prime:

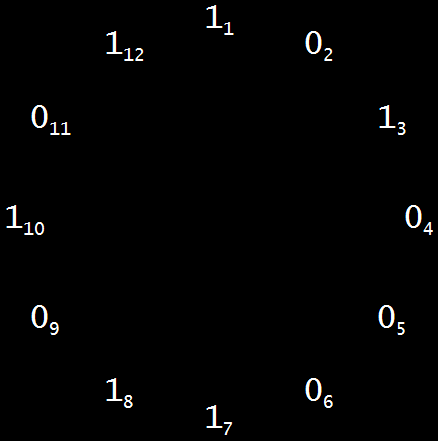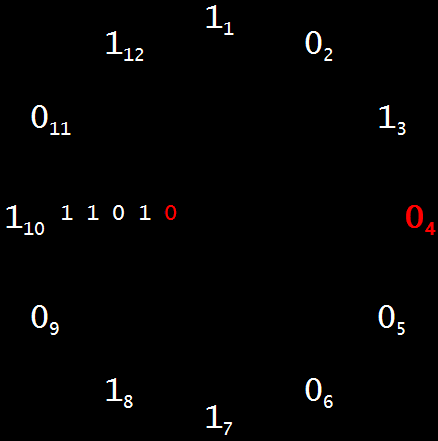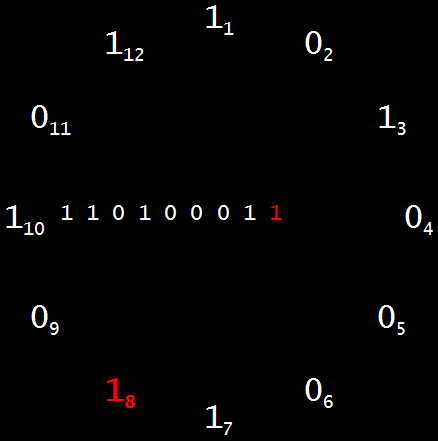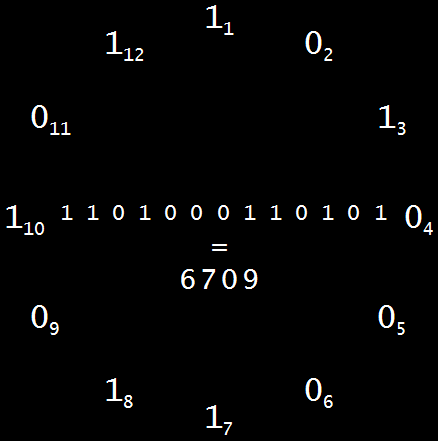
Ouroboros6709

Other Ouroboprimes produce brimes both clockwise and anti-clockwise, like 47 = 101,111.

Clockwise

101,111 = 47
111,011 = 59
111,101 = 61

Anti-Clockwise

111,101 = 61
111,011 = 59
101,111 = 47

If you demand the clock-rocked brime produce distinct primes, you sometimes get more in one direction than the other. Here is 151 = 10,010,111:

Clockwise

10,010,111 = 151
11,100,101 = 229

Anti-Clockwise

11,101,001 = 233
11,010,011 = 211
10,100,111 = 167
10,011,101 = 157

The most productive brime I’ve discovered so far is 2,326,439 = 1,000,110,111,111,110,100,111[2], which produces fifteen distinct primes:

Clockwise (7 brimes)

1,000,110,111,111,110,100,111 = 2326439
1,100,011,011,111,111,010,011 = 3260371
1,110,100,111,000,110,111,111 = 3830207
1,111,101,001,110,001,101,111 = 4103279
1,111,110,100,111,000,110,111 = 4148791
1,111,111,010,011,100,011,011 = 4171547
1,101,111,111,101,001,110,001 = 3668593

Anti-Clockwise (8 brimes)

1,110,010,111,111,110,110,001 = 3768241
1,100,101,111,111,101,100,011 = 3342179
1,111,111,011,000,111,001,011 = 4174283
1,111,110,110,001,110,010,111 = 4154263
1,111,101,100,011,100,101,111 = 4114223
1,111,011,000,111,001,011,111 = 4034143
1,110,110,001,110,010,111,111 = 3873983
1,000,111,001,011,111,111,011 = 2332667

Appendix: Deciminimalist Primes

Some primes in base ten use only the two most basic symbols too. That is, primes like 11[10], 101[10], 10111[10] and 1011001[10] are composed of only 1’s and 0’s. Furthermore, when these numbers are read as binary instead, they are still prime: 11[2] = 3, 101[2] = 5, 10111[2] = 23 and 1011001[2] = 89. Here is an incomplete list of these deciminimalist primes:

11[10] = 1,011[2]; 11[2] = 3[10] is also prime.

101[10] = 1,100,101[2]; 101[2] = 5[10] is also prime.

10,111[10] = 10,011,101,111,111[2]; 10,111[2] = 23[10] is also prime.

101,111[10] = 11,000,101,011,110,111[2]; 101,111[2] = 47[10] is also prime.

1,011,001[10] = 11,110,110,110,100,111,001[2]; 1,011,001[2] = 89[10] is also prime.

1,100,101[10] = 100,001,100,100,101,000,101[2]; 1,100,101[2] = 101[10] is also prime.

10,010,101[10] = 100,110,001,011,110,111,110,101[2]; 10,010,101[2] = 149[10] is also prime.

10,011,101[10] = 100,110,001,100,000,111,011,101[2]; 10,011,101[2] = 157[10] is also prime.

10,100,011[10] = 100,110,100,001,110,100,101,011[2]; 10,100,011[2] = 163[10] is also prime.

10,101,101[10] = 100,110,100,010,000,101,101,101[2]; 10,101,101[2] = 173[10] is also prime.

10,110,011[10] = 100,110,100,100,010,000,111,011[2]; 10,110,011[2] = 179[10] is also prime.

10,111,001[10] = 100,110,100,100,100,000,011,001[2].

11,000,111[10] = 101,001,111,101,100,100,101,111[2]; 11,000,111[2] = 199[10] is also prime.

11,100,101[10] = 101,010,010,101,111,111,000,101[2]; 11,100,101[2] = 229[10] is also prime.

11,110,111[10] = 101,010,011,000,011,011,011,111[2].

11,111,101[10] = 101,010,011,000,101,010,111,101[2].

100,011,001[10] = 101,111,101,100,000,101,111,111,001[2]; 100,011,001[2] = 281[10] is also prime.

100,100,111[10] = 101,111,101,110,110,100,000,001,111[2].

100,111,001[10] = 101,111,101,111,001,001,010,011,001[2]; 100,111,001[2] = 313[10] is also prime.

101,001,001[10] = 110,000,001,010,010,011,100,101,001[2].

101,001,011[10] = 110,000,001,010,010,011,100,110,011[2]; 101,001,011[2] = 331[10] is also prime.

101,001,101[10] = 110,000,001,010,010,011,110,001,101[2].

101,100,011[10] = 110,000,001,101,010,100,111,101,011[2].

101,101,001[10] = 110,000,001,101,010,110,111,001,001[2].

101,101,111[10] = 110,000,001,101,010,111,000,110,111[2]; 101,101,111[2] = 367[10] is also prime.

101,110,111[10] = 110,000,001,101,101,000,101,011,111[2].

101,111,011[10] = 110,000,001,101,101,010,011,100,011[2]; 101,111,011[2] = 379[10] is also prime.

101,111,111[10] = 110,000,001,101,101,010,101,000,111[2]; 101,111,111[2] = 383[10] is also prime.

110,010,101[10] = 110,100,011,101,001,111,011,110,101[2].

110,100,101[10] = 110,100,011,111,111,111,010,000,101[2]; 110,100,101[2] = 421[10] is also prime.

110,101,001[10] = 110,100,100,000,000,001,000,001,001[2].

110,110,001[10] = 110,100,100,000,010,010,100,110,001[2]; 110,110,001[2] = 433[10] is also prime.

110,111,011[10] = 110,100,100,000,010,100,100,100,011[2]; 110,111,011[2] = 443[10] is also prime.

Watch this Sbase

by in Mathematics and tagged , , , , , , , , , , , | Leave a comment

In standard notation, there are two ways to represent 2: 10, in base 2, and 2 in every other base. Accordingly, there are three ways to represent 3: 11 in base 2, 10 in base 3, and 3 in every other base. There are four ways to represent 4, five ways to represent 5, and so on. Now, suppose you sum all the digits of all the representations of n in the bases 2 to n, like this:

Σ(2) = 1+02 = 1
Σ(3) = 1+12 + 1+03 = 3 (+2)
Σ(4) = 1+0+02 + 1+13 + 1+04 = 4 (+1)
Σ(5) = 1+0+12 + 1+23 + 1+14 + 1+05 = 8 (+4)
Σ(6) = 1+1+02 + 2+03 + 1+24 + 1+15 + 1+06 = 10 (+2)
Σ(7) = 1+1+12 + 2+13 + 1+34 + 1+25 + 1+16 + 1+07 = 16 (+6)
Σ(8) = 1+0+0+02 + 2+23 + 2+04 + 1+35 + 1+26 + 1+17 + 1+08 = 17 (+1)
Σ(9) = 1+0+0+12 + 1+0+03 + 2+14 + 1+45 + 1+36 + 1+27 + 1+18 + 1+09 = 21 (+4)
Σ(10) = 1+0+1+02 + 1+0+13 + 2+24 + 2+05 + 1+46 + 1+37 + 1+28 + 1+19 + 1+010 = 25 (+4)

It seems reasonable to suppose that as n increases, so the all-digit-sum of n increases. But that isn’t always the case: occasionally it decreases. Here are the sums for n=11..100 (with prime factors when the sum is composite):

Σ(11) = 35 = 5·7 (+10)
Σ(12) = 34 = 2·17 (-1)
Σ(13) = 46 = 2·23 (+12)
Σ(14) = 52 = 22·13 (+6)
Σ(15) = 60 = 22·3·5 (+8)
Σ(16) = 58 = 2·29 (-2)
Σ(17) = 74 = 2·37 (+16)
Σ(18) = 73 (-1)
Σ(19) = 91 = 7·13 (+18)
Σ(20) = 92 = 22·23 (+1)
Σ(21) = 104 = 23·13 (+12)
Σ(22) = 114 = 2·3·19 (+10)
Σ(23) = 136 = 23·17 (+22)
Σ(24) = 128 = 27 (-8)
Σ(25) = 144 = 24·32 (+16)
Σ(26) = 156 = 22·3·13 (+12)
Σ(27) = 168 = 23·3·7 (+12)
Σ(28) = 171 = 32·19 (+3)
Σ(29) = 199 (+28)
Σ(30) = 193 (-6)
Σ(31) = 223 (+30)
Σ(32) = 221 = 13·17 (-2)
Σ(33) = 241 (+20)
Σ(34) = 257 (+16)
Σ(35) = 281 (+24)
Σ(36) = 261 = 32·29 (-20)
Σ(37) = 297 = 33·11 (+36)
Σ(38) = 315 = 32·5·7 (+18)
Σ(39) = 339 = 3·113 (+24)
Σ(40) = 333 = 32·37 (-6)
Σ(41) = 373 (+40)
Σ(42) = 367 (-6)
Σ(43) = 409 (+42)
Σ(44) = 416 = 25·13 (+7)
Σ(45) = 430 = 2·5·43 (+14)
Σ(46) = 452 = 22·113 (+22)
Σ(47) = 498 = 2·3·83 (+46)
Σ(48) = 472 = 23·59 (-26)
Σ(49) = 508 = 22·127 (+36)
Σ(50) = 515 = 5·103 (+7)
Σ(51) = 547 (+32)
Σ(52) = 556 = 22·139 (+9)
Σ(53) = 608 = 25·19 (+52)
Σ(54) = 598 = 2·13·23 (-10)
Σ(55) = 638 = 2·11·29 (+40)
Σ(56) = 634 = 2·317 (-4)
Σ(57) = 670 = 2·5·67 (+36)
Σ(58) = 698 = 2·349 (+28)
Σ(59) = 756 = 22·33·7 (+58)
Σ(60) = 717 = 3·239 (-39)
Σ(61) = 777 = 3·7·37 (+60)
Σ(62) = 807 = 3·269 (+30)
Σ(63) = 831 = 3·277 (+24)
Σ(64) = 819 = 32·7·13 (-12)
Σ(65) = 867 = 3·172 (+48)
Σ(66) = 861 = 3·7·41 (-6)
Σ(67) = 927 = 32·103 (+66)
Σ(68) = 940 = 22·5·47 (+13)
Σ(69) = 984 = 23·3·41 (+44)
Σ(70) = 986 = 2·17·29 (+2)
Σ(71) = 1056 = 25·3·11 (+70)
Σ(72) = 1006 = 2·503 (-50)
Σ(73) = 1078 = 2·72·11 (+72)
Σ(74) = 1114 = 2·557 (+36)
Σ(75) = 1140 = 22·3·5·19 (+26)
Σ(76) = 1155 = 3·5·7·11 (+15)
Σ(77) = 1215 = 35·5 (+60)
Σ(78) = 1209 = 3·13·31 (-6)
Σ(79) = 1287 = 32·11·13 (+78)
Σ(80) = 1263 = 3·421 (-24)
Σ(81) = 1293 = 3·431 (+30)
Σ(82) = 1333 = 31·43 (+40)
Σ(83) = 1415 = 5·283 (+82)
Σ(84) = 1368 = 23·32·19 (-47)
Σ(85) = 1432 = 23·179 (+64)
Σ(86) = 1474 = 2·11·67 (+42)
Σ(87) = 1530 = 2·32·5·17 (+56)
Σ(88) = 1530 = 2·32·5·17 (=)
Σ(89) = 1618 = 2·809 (+88)
Σ(90) = 1572 = 22·3·131 (-46)
Σ(91) = 1644 = 22·3·137 (+72)
Σ(92) = 1663 (+19)
Σ(93) = 1723 (+60)
Σ(94) = 1769 = 29·61 (+46)
Σ(95) = 1841 = 7·263 (+72)
Σ(96) = 1784 = 23·223 (-57)
Σ(97) = 1880 = 23·5·47 (+96)
Σ(98) = 1903 = 11·173 (+23)
Σ(99) = 1947 = 3·11·59 (+44)
Σ(100) = 1923 = 3·641 (-24)

The sum usually increases, occasionally decreases. In one case, when 87 = n = 88, it stays the same. This also happens when 463 = n = 464, where Σ(463) = Σ(464) = 39,375. Does it happen again? I don’t know. The ratio of sum-ups to sum-downs seems to tend towards 3:1. Is that the exact ratio at infinity? I don’t know. Watch this sbase.