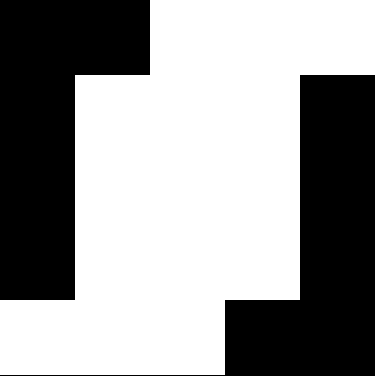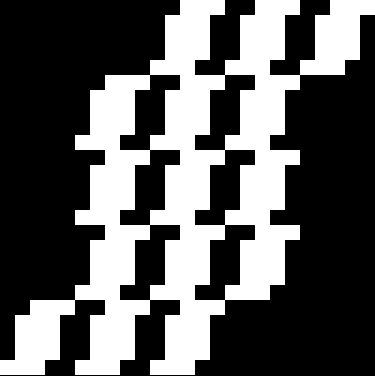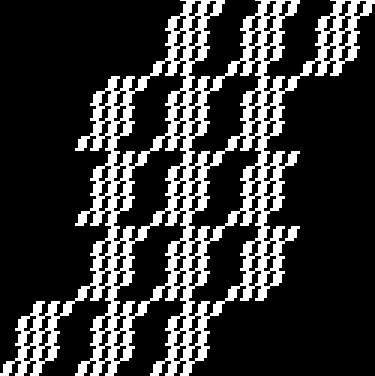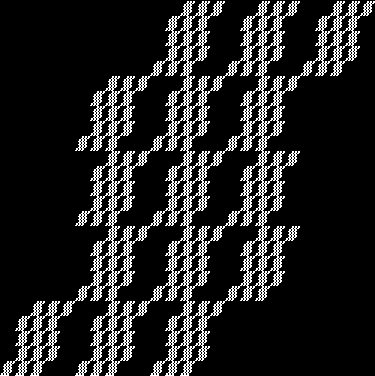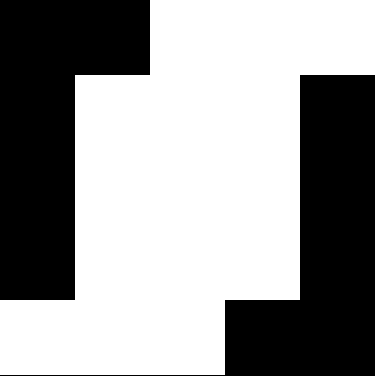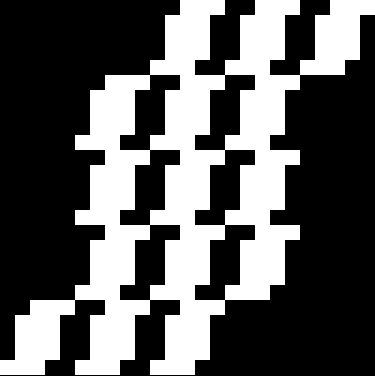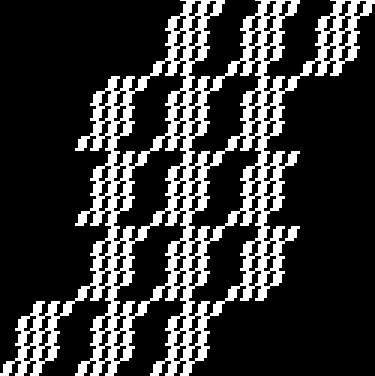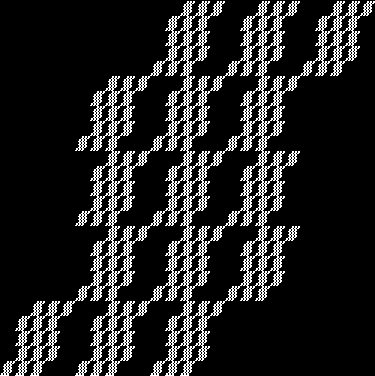In “M.I.P. Trip”, I looked at fractals like this, in which a square is divided repeatedly into a pattern of smaller squares:
As you can see, the sub-squares appear within the bounds of the original square. But what if some of the sub-squares appear beyond the bounds of the original square? Then a new family of fractals is born, the over-fractals:
The Latin phrase multum in parvo means “much in little”. It’s a good way of describing the construction of fractals, where the application of very simple rules can produce great complexity and beauty. For example, what could be simpler than dividing a square into smaller squares and discarding some of the smaller squares?
Yet repeated applications of divide-and-discard can produce complexity out of even a 2×2 square. Divide a square into four squares, discard one of the squares, then repeat with the smaller squares, like this:
Increase the sides of the square by a little and you increase the number of fractals by a lot. A 3×3 square yields these fractals:
And the 4×4 and 5×5 fractals yield more:
A regular hexagon can be divided into six equilateral triangles. An equilateral triangle can be divided into three more equilateral triangles and a regular hexagon. If you discard the three triangles and repeat, you create a fractal, like this:
Adjusting the sides of the internal hexagon creates new fractals:
Discarding a hexagon after each subdivision creates new shapes:
And you can start with another regular polygon, divide it into triangles, then proceed with the hexagons:
Overlord In Terms of Core Issues Around Maximal Engagement with Key Notions of the Über-Feral 