Tag Archives: mathematics

Thrice Dice Twice

by in Mathematics, Probability, Randomness and tagged , , , , , , , , , , , , , , , | Leave a comment

A once very difficult but now very simple problem in probability from Ian Stewart’s Do Dice Play God? (2019):

For three dice [Girolamo] Cardano solved a long-standing conundrum [in the sixteenth century]. Gamblers had long known from experience that when throwing three dice, a total of 10 is more likely than 9. This puzzled them, however, because there are six ways to get a total of 10:

1+4+5; 1+3+6; 2+4+4; 2+2+6; 2+3+5; 3+3+4

But also six ways to get a total of 9:

1+2+6; 1+3+5; 1+4+4; 2+2+5; 2+3+4; 3+3+3

So why does 10 occur more often?

To see the answer, imagine throwing three dice of different colors: red, blue and yellow. How many ways can you get 9 and how many ways can you get 10?

Roll Total=9 Dice #1 (Red) Dice #2 (Blue) Dice #3 (Yellow)
01 9 = 1 2 6
02 9 = 1 3 5
03 9 = 1 4 4
04 9 = 1 5 3
05 9 = 1 6 2
06 9 = 2 1 6
07 9 = 2 2 5
08 9 = 2 3 4
09 9 = 2 4 3
10 9 = 2 5 2
11 9 = 2 6 1
12 9 = 3 1 5
13 9 = 3 2 4
14 9 = 3 3 3
15 9 = 3 4 2
16 9 = 3 5 1
17 9 = 4 1 4
18 9 = 4 2 3
19 9 = 4 3 2
20 9 = 4 4 1
21 9 = 5 1 3
22 9 = 5 2 2
23 9 = 5 3 1
24 9 = 6 1 2
25 9 = 6 2 1
Roll Total=10 Dice #1 (Red) Dice #2 (Blue) Dice #3 (Yellow)
01 10 = 1 3 6
02 10 = 1 4 5
03 10 = 1 5 4
04 10 = 1 6 3
05 10 = 2 2 6
06 10 = 2 3 5
07 10 = 2 4 4
08 10 = 2 5 3
09 10 = 2 6 2
10 10 = 3 1 6
11 10 = 3 2 5
12 10 = 3 3 4
13 10 = 3 4 3
14 10 = 3 5 2
15 10 = 3 6 1
16 10 = 4 1 5
17 10 = 4 2 4
18 10 = 4 3 3
19 10 = 4 4 2
20 10 = 4 5 1
21 10 = 5 1 4
22 10 = 5 2 3
23 10 = 5 3 2
24 10 = 5 4 1
25 10 = 6 1 3
26 10 = 6 2 2
27 10 = 6 3 1

Back to Drac’ #2

by in Dragon Curves, Fractals, Geometry, Mathematics and tagged , , , , , , , , , , , , , , , | Leave a comment

Boring, dull, staid, stiff, everyday, ordinary, unimaginative, unexceptional, crashingly conventional — the only interesting thing about squares is the number of ways you can say how uninteresting they are. Unlike triangles, which vary endlessly and entertainingly, squares are square in every sense of the word.

And they don’t get any better if you tilt them, as here:

Sub-squares from gray square (with corner-numbers)

Nothing interesting can emerge from that set of squares. Or can it? As I showed in Curvous Energy, it can. Suppose that the gray square is dividing into the colored squares like a kind of amoeba. And suppose that the colored squares divide in their turn. So square divides into sub-squares and sub-squares divide into sub-sub-squares. And so on. And all the squares keep the same relative orientation.

What happens if the gray square divides into sub-squares sq2 and sq9? And then sq2 and sq9 each divide into their own sq2 and sq9? And so on. Something very unsquare-like happens:

Square-split stage #1

Stage #2

Square-split #3

Square-split #4

Square-split #5

Square-split #6

Square-split #7

Square-split #8

Square-split #9

Square-split #10

Square-split #11

Square-split #12

Square-split #13

Square-split #14

Square-split #15

Square-split #16

Square-split (animated)

The square-split creates a beautiful fractal known as a dragon-curve:

Dragon-curve

Dragon-curve (red)

And dragon-curves, at various angles and in various sizes, emerge from every other possible pair of sub-squares:

Lots of dragon-curves

And you get other fractals if you manipulate the sub-squares, so that the corners are rotated or reverse-rotated:

Rotation = 1,2 (sub-square #1 unchanged, in sub-square #2 corner 1 becomes corner 2, 2 → 3, 3 → 4, 4 → 1)

rot = 1,2 (animated)

rot = 1,2 (colored)

rot = 1,5 (in sub-square #2 corner 1 stays the same, 4 → 2, 3 stays the same, 2 → 4)

rot = 1,5 (anim)

rot = 4,7 (sub-square #2 flipped and rotated)

rot = 4,7 (anim)

rot = 4,7 (col)

rot = 4,8

rot = 4,8 (anim)

rot = 4,8 (col)

sub-squares = 2,8; rot = 5,6

sub-squares = 2,8; rot = 5,6 (anim)

sub-squares = 2,8; rot = 5,6 (col)

Another kind of dragon-curve — rot = 3,2

rot = 3,2 (anim)

rot = 3,2 (col)

sub-squares = 4,5; rot = 3,9

sub-squares = 4,5; rot = 3,9 (anim)

sub-squares = 4,5; rot = 3,9 (col)

Elsewhere other-accessible…

• Curvous Energy — a first look at dragon-curves
• Back to Drac’ — a second look at dragon-curves

Rollercoaster Rules

by in Digit-sums, Integer Sequences, Mathematics, Repdigits and tagged , , , , , , , , , , , , , , , , , , | Leave a comment

n += digsum(n). It’s one of my favorite integer sequences — a rollercoaster to infinity. It works like this: you take a number, sum its digits, add the sum to the original number, and repeat:


1 → 2 → 4 → 8 → 16 → 23 → 28 → 38 → 49 → 62 → 70 → 77 → 91 → 101 → 103 → 107 → 115 → 122 → 127 → 137 → 148 → 161 → 169 → 185 → 199 → 218 → 229 → 242 → 250 → 257 → 271 → 281 → 292 → 305 → 313 → 320 → 325 → 335 → 346 → 359 → 376 → 392 → 406 → 416 → 427 → 440 → 448 → 464 → 478 → 497 → 517 → 530 → 538 → 554 → 568 → 587 → 607 → 620 → 628 → 644 → 658 → 677 → 697 → 719 → 736 → 752 → 766 → 785 → 805 → 818 → 835 → 851 → 865 → 884 → 904 → 917 → 934 → 950 → 964 → 983 → 1003 → 1007 → 1015 → 1022 → 1027 → 1037 → 1048 → 1061 → 1069 → 1085 → 1099 → 1118 → 1129 → 1142 → 1150 → 1157 → 1171 → 1181 → 1192 → 1205 → ...

I call it a rollercoaster to infinity because the digit-sum constantly rises and falls as n gets bigger and bigger. The most dramatic falls are when n gets one digit longer (except on the first occasion):


... → 8 (digit-sum=8) → 16 (digit-sum=7) → ...
... → 91 (ds=10) → 101 (ds=2) → ...
... → 983 (ds=20) → 1003 (ds=4) → ...
... → 9968 (ds=32) → 10000 (ds=1) → ...
... → 99973 (ds=37) → 100010 (ds=2) → ...
... → 999959 (ds=50) → 1000009 (ds=10) → ...
... → 9999953 (ds=53) → 10000006 (ds=7) → ...
... → 99999976 (ds=67) → 100000043 (ds=8) → ...
... → 999999980 (ds=71) → 1000000051 (ds=7) → ...
... → 9999999962 (ds=80) → 10000000042 (ds=7) → ...
... → 99999999968 (ds=95) → 100000000063 (ds=10) → ...
... → 999999999992 (ds=101) → 1000000000093 (ds=13) → ...

Look at 9968 → 10000, when the digit-sum goes from 32 to 1. That’s only the second time that digsum(n) = 1 in the sequence. Does it happen again? I don’t know.

And here’s something else I don’t know. Suppose you introduce a rule for the rollercoaster of n += digsum(n). You buy a ticket with a number on it: 1, 2, 3, 4, 5… Then you get on the rollercoaster powered by with that number. Now here’s the rule: Your ride on the rollercoaster ends when n += digsum(n) yields a rep-digit, i.e., a number whose digits are all the same. Here are the first few rides on the rollercoaster:


1 → 2 → 4 → 8 → 16 → 23 → 28 → 38 → 49 → 62 → 70 → 77
2 → 4 → 8 → 16 → 23 → 28 → 38 → 49 → 62 → 70 → 77
3 → 6 → 12 → 15 → 21 → 24 → 30 → 33
4 → 8 → 16 → 23 → 28 → 38 → 49 → 62 → 70 → 77
5 → 10 → 11
6 → 12 → 15 → 21 → 24 → 30 → 33
7 → 14 → 19 → 29 → 40 → 44
8 → 16 → 23 → 28 → 38 → 49 → 62 → 70 → 77
9 → 18 → 27 → 36 → 45 → 54 → 63 → 72 → 81 → 90 → 99
10 → 11
11 → 13 → 17 → 25 → 32 → 37 → 47 → 58 → 71 → 79 → 95 → 109 → 119 → 130 → 134 → 142 → 149 → 163 → 173 → 184 → 197 → 214 → 221 → 226 → 236 → 247 → 260 → 268 → 284 → 298 → 317 → 328 → 341 → 349 → 365 → 379 → 398 → 418 → 431 → 439 → 455 → 469 → 488 → 508 → 521 → 529 → 545 → 559 → 578 → 598 → 620 → 628 → 644 → 658 → 677 → 697 → 719 → 736 → 752 → 766 → 785 → 805 → 818 → 835 → 851 → 865 → 884 → 904 → 917 → 934 → 950 → 964 → 983 → 1003 → 1007 → 1015 → 1022 → 1027 → 1037 → 1048 → 1061 → 1069 → 1085 → 1099 → 1118 → 1129 → 1142 → 1150 → 1157 → 1171 → 1181 → 1192 → 1205 → 1213 → 1220 → 1225 → 1235 → 1246 → 1259 → 1276 → 1292 → 1306 → 1316 → 1327 → 1340 → 1348 → 1364 → 1378 → 1397 → 1417 → 1430 → 1438 → 1454 → 1468 → 1487 → 1507 → 1520 → 1528 → 1544 → 1558 → 1577 → 1597 → 1619 → 1636 → 1652 → 1666 → 1685 → 1705 → 1718 → 1735 → 1751 → 1765 → 1784 → 1804 → 1817 → 1834 → 1850 → 1864 → 1883 → 1903 → 1916 → 1933 → 1949 → 1972 → 1991 → 2011 → 2015 → 2023 → 2030 → 2035 → 2045 → 2056 → 2069 → 2086 → 2102 → 2107 → 2117 → 2128 → 2141 → 2149 → 2165 → 2179 → 2198 → 2218 → 2231 → 2239 → 2255 → 2269 → 2288 → 2308 → 2321 → 2329 → 2345 → 2359 → 2378 → 2398 → 2420 → 2428 → 2444 → 2458 → 2477 → 2497 → 2519 → 2536 → 2552 → 2566 → 2585 → 2605 → 2618 → 2635 → 2651 → 2665 → 2684 → 2704 → 2717 → 2734 → 2750 → 2764 → 2783 → 2803 → 2816 → 2833 → 2849 → 2872 → 2891 → 2911 → 2924 → 2941 → 2957 → 2980 → 2999 → 3028 → 3041 → 3049 → 3065 → 3079 → 3098 → 3118 → 3131 → 3139 → 3155 → 3169 → 3188 → 3208 → 3221 → 3229 → 3245 → 3259 → 3278 → 3298 → 3320 → 3328 → 3344 → 3358 → 3377 → 3397 → 3419 → 3436 → 3452 → 3466 → 3485 → 3505 → 3518 → 3535 → 3551 → 3565 → 3584 → 3604 → 3617 → 3634 → 3650 → 3664 → 3683 → 3703 → 3716 → 3733 → 3749 → 3772 → 3791 → 3811 → 3824 → 3841 → 3857 → 3880 → 3899 → 3928 → 3950 → 3967 → 3992 → 4015 → 4025 → 4036 → 4049 → 4066 → 4082 → 4096 → 4115 → 4126 → 4139 → 4156 → 4172 → 4186 → 4205 → 4216 → 4229 → 4246 → 4262 → 4276 → 4295 → 4315 → 4328 → 4345 → 4361 → 4375 → 4394 → 4414 → 4427 → 4444

The 11-ticket is much better value than the tickets for 1..10. Bigger numbers behave like this:


1252 → 4444
1253 → 4444
1254 → 888888
1255 → 4444
1256 → 4444
1257 → 888888
1258 → 4444
1259 → 4444
1260 → 9999
1261 → 4444
1262 → 4444
1263 → 888888
1264 → 4444
1265 → 4444
1266 → 888888
1267 → 4444
1268 → 4444
1269 → 9999
1270 → 4444
1271 → 4444
1272 → 888888
1273 → 4444
1274 → 4444

Then all at once, a number-ticket turns golden and the rollercoaster-ride doesn’t end. So far, at least. I’ve tried, but I haven’t been able to find a rep-digit for 3515 and 3529 = 3515+digsum(3515) and so on:


3509 → 4444
3510 → 9999
3511 → 4444
3512 → 4444
3513 → 888888
3514 → 4444
3515 → ?
3516 → 888888
3517 → 4444
3518 → 4444
3519 → 9999
3520 → 4444
3521 → 4444
3522 → 888888
3523 → 4444
3524 → 4444
3525 → 888888
3526 → 4444
3527 → 4444
3528 → 9999
3529 → ?
3530 → 4444
3531 → 888888
3532 → 4444

Does 3515 ever yield a rep-digit for n += digsum(n)? It’s hard to believe it doesn’t, but I’ve no idea how to prove that it does. Except by simply riding the rollercoaster. And if the ride with the 3515-ticket never reaches a rep-digit, the rollercoaster will never let you know. How could it?

But here’s an example in base 23 of how a ticket for n+1 can give you a dramatically longer ride than a ticket for n and n+2:


MI → EEE (524 → 7742)
MJ → EEE (525 → 7742)
MK → 444 (526 → 2212)
ML → 444 (527 → 2212)
MM → MMMMMM (528 → 148035888)
100 → 444 (529 → 2212)
101 → 444 (530 → 2212)
102 → EEE (531 → 7742)
103 → 444 (532 → 2212)
104 → 444 (533 → 2212)
105 → EEE (534 → 7742)
106 → EEE (535 → 7742)
107 → 444 (536 → 2212)
108 → EEE (537 → 7742)
109 → 444 (538 → 2212)
10A → MMMMMM (539 → 148035888)
10B → EEE (540 → 7742)
10C → EEE (541 → 7742)
10D → EEE (542 → 7742)
10E → EEE (543 → 7742)
10F → 444 (544 → 2212)
10G → EEE (545 → 7742)
10H → EEE (546 → 7742)
10I → EEE (547 → 7742)
10J → 444 (548 → 2212)
10K → 444 (549 → 2212)
10L → MMMMMM (550 → 148035888)
10M → EEE (551 → 7742)
110 → EEE (552 → 7742)

More Mythical Mathicality

by in Art, Fractals, Mathematics, Post-Weird and tagged , , , , , , , | Leave a comment

In a prev-previous post, I looked at this interesting fractal image on the front cover of a Ray Bradbury book:

Cover of Ray Bradbury’s I Sing the Body Electric (1969)

It seems obvious that the image is created from photographs: only the body of the centaur is drawn by hand. And here’s my attempt at extending the fractality of the image:

Further fractality for the centaur
Elsewhere other-accessible

• Mythical Mathical — Man-Horse! — the pre-previous post about the fractal centaur

Think Inc #2

by in Chaos Game, Fractals, Geometry, Mathematics, Squares and tagged , , , , , , , , , , , , , , | Leave a comment

In a pre-previous post called “Think Inc”, I looked at the fractals created by a point first jumping halfway towards the vertex of a square, then using a set of increments to decide which vertex to jump towards next. For example, if the inc-set was [0, 1, 3], the point would jump next towards the same vertex, v[i]+0, or the vertex immediately clockwise, v[i]+1, or the vertex immediately anti-clockwise, v[i]+3. And it would trace all possible routes using that inc-set. Then I added refinements to the process like giving the point extra jumping-targets half-way along each side.

Here are some more variations on the inc-set theme using two and three extra jumping-targets along each side of the square. First of all, try two extra jumping-targets along each side and a set of three increments:

inc = 0, 1, 6

inc = 0, 2, 6

inc = 0, 2, 8

inc = 0, 3, 6

inc = 0, 3, 9

inc = 0, 4, 8

inc = 0, 5, 6

inc = 0, 5, 7

inc = 1, 6, 11

inc = 2, 6, 10

inc = 3, 6, 9

Now try two extra jumping-targets along each side and a set of four increments:

inc = 0, 1, 6, 11

inc = 0, 2, 8, 10

inc = 0, 3, 7, 9

inc = 0, 4, 8, 10

inc = 0, 5, 6, 7

inc = 0, 5, 7, 8

inc = 1, 6, 7, 9

inc = 1, 4, 6, 11

inc = 1, 5, 7, 11

inc = 2, 4, 8, 10

inc = 3, 5, 7, 9

And finally, three extra jumping-targets along each side and a set of three increments:

inc = 0, 3, 13

inc = 0, 4, 8

inc = 0, 4, 12

inc = 0, 5, 11

inc = 0, 6, 9

inc = 0, 7, 9

Previously Pre-Posted

• Think Inc — an earlier look at inc-set fractals

Mythical Mathical — Man-Horse!

by in Art, Fractals, Mathematics and tagged , , , , , , , , , | 1 Comment
Cover of Ray Bradbury’s I Sing the Body Electric (1969), published by Corgi in 1972

That’s a striking cover — and more than that. The blog where I found the cover says this: “This very odd cover clearly features a heavily rouged glam rock centaur with a rather natty feather-cut hairstyle flexing his biceps, his forearms transmogrifying into miniature bicep flexing glam rock figures. I think I’m slowly losing the plot here.”

Losing the plot? No, losing the mathical in the mythical. The artist has started to make the centaur into a fractal. Or rather, the artist has started to make more explicit what is already there in the human body. As I wrote pre-previously:

Fingers are fractal. Where a tree has a trunk, branches and twigs, a human being has a torso, arms and fingers. And human beings move in fractal ways. We use our legs to move large distances, then reach out with our arms over smaller distances, then move our fingers over smaller distances still. We’re fractal beings, inside and out, brains and blood-vessels, fingers and toes. — “Fingering the Frigit”

Here’s my attempt at extending the fractality of the centaur:

Further fractality for the centaur

Elsewhere Other-Accessible

• More Mythical Mathicality

Sliv and Let Tri

by in Integer Sequences, Mathematics and tagged , , , , , , , , , , , , , , , , , , , | Leave a comment
“Fluvius, planus et altus, in quo et agnus ambulet et elephas natet,” wrote Pope Gregory the Great (540-604). “There’s a river, wide and deep, where a lamb may wade and an elephant swim.” He was talking about the Word of God, but you can easily apply his words to mathematics. However, in the river of mathematics, the very shallow and the very deep are often a single step apart.

Here’s a good example. Take the integer 2. How many different ways can it be represented as an sum of separate integers? Easy. First of all it can be represented as itself: 2 = 2. Next, it can be represented as 2 = 1 + 1. And that’s it. There are two partitions of 2, as mathematicians say:

2 = 2 = 1+1 (p=2)


Now try 3, 4, 5, 6:

3 = 3 = 1+2 = 1+1+1 (p=3)
4 = 4 = 1+3 = 2+2 = 1+1+2 = 1+1+1+1 (p=5)
5 = 5 = 1+4 = 2+3 = 1+1+3 = 1+2+2 = 1+1+1+2 = 1+1+1+1+1 (p=7)
6 = 6 = 1+5 = 2+4 = 3+3 = 1+1+4 = 1+2+3 = 2+2+2 = 1+1+1+3 = 1+1+2+2 = 1+1+1+1+2 = 1+1+1+1+1+1 (p=11)


So the partitions of 2, 3, 4, 5, 6 are 2, 3, 5, 7, 11. That’s interesting — the partition-counts are the prime numbers in sequence. So you might conjecture that p(7) = 13 and p(8) = 17. Alas, you’d be wrong. Here are the partitions of n = 1..10:

1 = 1 (p=1)
2 = 2 = 1+1 (p=2)
3 = 3 = 1+2 = 1+1+1 (p=3)
4 = 4 = 1+3 = 2+2 = 1+1+2 = 1+1+1+1 (p=5)
5 = 5 = 1+4 = 2+3 = 1+1+3 = 1+2+2 = 1+1+1+2 = 1+1+1+1+1 (p=7)
6 = 6 = 1+5 = 2+4 = 3+3 = 1+1+4 = 1+2+3 = 2+2+2 = 1+1+1+3 = 1+1+2+2 = 1+1+1+1+2 = 1+1+1+1+1+1 (p=11)
7 = 7 = 1+6 = 2+5 = 3+4 = 1+1+5 = 1+2+4 = 1+3+3 = 2+2+3 = 1+1+1+4 = 1+1+2+3 = 1+2+2+2 = 1+1+1+1+3 = 1+1+1+2+2 = 1+1+1+1+1+2 = 1+1+1+1+1+1+1 (p=15)
8 = 8 = 1+7 = 2+6 = 3+5 = 4+4 = 1+1+6 = 1+2+5 = 1+3+4 = 2+2+4 = 2+3+3 = 1+1+1+5 = 1+1+2+4 = 1+1+3+3 = 1+2+2+3 = 2+2+2+2 = 1+1+1+1+4 = 1+1+1+2+3 = 1+1+2+2+2 = 1+1+1+1+1+3 = 1+1+1+1+2+2 = 1+1+1+1+1+1+2 = 1+1+1+1+1+1+1+1 (p=22)
9 = 9 = 1+8 = 2+7 = 3+6 = 4+5 = 1+1+7 = 1+2+6 = 1+3+5 = 1+4+4 = 2+2+5 = 2+3+4 = 3+3+3 = 1+1+1+6 = 1+1+2+5 = 1+1+3+4 = 1+2+2+4 = 1+2+3+3 = 2+2+2+3 = 1+1+1+1+5 = 1+1+1+2+4 = 1+1+1+3+3 = 1+1+2+2+3 = 1+2+2+2+2 = 1+1+1+1+1+4 = 1+1+1+1+2+3 = 1+1+1+2+2+2 = 1+1+1+1+1+1+3 = 1+1+1+1+1+2+2 = 1+1+1+1+1+1+1+2 = 1+1+1+1+1+1+1+1+1 (p=30)
10 = 10 = 1+9 = 2+8 = 3+7 = 4+6 = 5+5 = 1+1+8 = 1+2+7 = 1+3+6 = 1+4+5 = 2+2+6 = 2+3+5 = 2+4+4 = 3+3+4 = 1+1+1+7 = 1+1+2+6 = 1+1+3+5 = 1+1+4+4 = 1+2+2+5 = 1+2+3+4 = 1+3+3+3 = 2+2+2+4 = 2+2+3+3 = 1+1+1+1+6 = 1+1+1+2+5 = 1+1+1+3+4 = 1+1+2+2+4 = 1+1+2+3+3 = 1+2+2+2+3 = 2+2+2+2+2 = 1+1+1+1+1+5 = 1+1+1+1+2+4 = 1+1+1+1+3+3 = 1+1+1+2+2+3 = 1+1+2+2+2+2 = 1+1+1+1+1+1+4 = 1+1+1+1+1+2+3 = 1+1+1+1+2+2+2 = 1+1+1+1+1+1+1+3 = 1+1+1+1+1+1+2+2 = 1+1+1+1+1+1+1+1+2 = 1+1+1+1+1+1+1+1+1+1 (p=42)


It’s very simple to understand what a partition is, but very difficult to say how many partitions, p(n), a particular number will have. Here’s a partition: 11 = 4 + 3 + 2 + 2. But what is p(11)? Is there a formula for the sequence of p(n)?

1, 2, 3, 5, 7, 11, 15, 22, 30, 42, 56, 77, 101, 135, 176, 231, 297, 385, 490, 627, 792, 1002, 1255, 1575, 1958, 2436, 3010, 3718, 4565, 5604, 6842, 8349, 10143, 12310, 14883, 17977, 21637, 26015, 3118 5, 37338, 44583, 53174, 63261... (A000041 at the OEIS)

Yes, there is a formula, but it is very difficult to understand the Partition function that supplies it. So that part of the river of mathematics is very deep. But a step away the river of mathematics is very shallow. Here’s another question: If you multiply the numbers in a partition of n, what’s the largest possible product? Try using the partitions of 5:

4 = 1 * 4
6 = 2 * 3
3 = 1 * 1 * 3
4 = 1 * 2 * 2
2 = 1 * 1 * 1 * 2
1 = 1 * 1 * 1 * 1 * 1

The largest product is 6 = 2 * 3. So the answer is easy for n = 5, but I assumed that as n got bigger, the largest product got more interesting, using a subtler and subtler mix of prime factors. I was wrong. You don’t have to struggle to find a formula for what you might call the maximum multiplicity of the partitions of n:

1 = 1 (n=1)
2 = 2 (n=2)
3 = 3 (n=3)
4 = 2 * 2 (n=4)
6 = 2 * 3 (n=5)
9 = 3 * 3 (n=6)
12 = 2 * 2 * 3 (n=7)
18 = 2 * 3 * 3 (n=8)
27 = 3 * 3 * 3 (n=9)
36 = 2 * 2 * 3 * 3 (n=10)
54 = 2 * 3 * 3 * 3 (n=11)
81 = 3 * 3 * 3 * 3 (n=12)
108 = 2 * 2 * 3 * 3 * 3 (n=13)
162 = 2 * 3 * 3 * 3 * 3 162(n=14)
243 = 3 * 3 * 3 * 3 * 3 (n=15)
324 = 2 * 2 * 3 * 3 * 3 * 3 (n=16)
486 = 2 * 3 * 3 * 3 * 3 * 3 (n=17)
729 = 3 * 3 * 3 * 3 * 3 * 3 (n=18)


It’s easy to see why the greatest prime factor is always 3. If you use 5 or 7 as a factor, the product can always be beaten by splitting the 5 into 2*3 or the 7 into 2*2*3:

15 = 3 * 5 < 18 = 3 * 2*3 (n=8)
14 = 2 * 7 < 24 = 2 * 2*2*3 (n=9)
35 = 5 * 7 < 72 = 2*3 * 2*2*3 (n=12)

And if you’re using 7 → 2*2*3 as factors, you can convert them to 1*3*3, then add the 1 to another factor to make a bigger product still:

14 = 2 * 7 < 24 = 2 * 2*2*3 < 27 = 3 * 3 * 3 (n=9)
35 = 5 * 7 < 72 = 2*3 * 2*2*3 < 81 = 3 * 3 * 3 * 3 (n=12)

Post-Performative Post-Scriptum

The title of this post is, of course, a paronomasia on core Beatles album Live and Let Die (1954). But what does it mean? Well, if you think of the partitions of n as slivers of n, then you sliv n to find its partitions:

9 = 9 = 1+8 = 2+7 = 3+6 = 4+5 = 1+1+7 = 1+2+6 = 1+3+5 = 1+4+4 = 2+2+5 = 2+3+4 = 3+3+3 = 1+1+1+6 = 1+1+2+5 = 1+1+3+4 = 1+2+2+4 = 1+2+3+3 = 2+2+2+3 = 1+1+1+1+5 = 1+1+1+2+4 = 1+1+1+3+3 = 1+1+2+2+3 = 1+2+2+2+2 = 1+1+1+1+1+4 = 1+1+1+1+2+3 = 1+1+1+2+2+2 = 1+1+1+1+1+1+3 = 1+1+1+1+1+2+2 = 1+1+1+1+1+1+1+2 = 1+1+1+1+1+1+1+1+1 (p=30)

And when you find the greatest product among those partitions, you let 3 or “tri” work its multiplicative magic. So you “Sliv and Let Tri”:

8 = 1 * 8
14 = 2 * 7
18 = 3 * 6
20 = 4 * 5
7 = 1 * 1 * 7
12 = 1 * 2 * 6
15 = 1 * 3 * 5
16 = 1 * 4 * 4
20 = 2 * 2 * 5
24 = 2 * 3 * 4
27 = 3 * 3 * 3 ←
6 = 1 * 1 * 1 * 6
10 = 1 * 1 * 2 * 5
12 = 1 * 1 * 3 * 4
16 = 1 * 2 * 2 * 4
12 = 1 * 2 * 3 * 3
24 = 2 * 2 * 2 * 3
5 = 1 * 1 * 1 * 1 * 5
8 = 1 * 1 * 1 * 2 * 4
9 = 1 * 1 * 1 * 3 * 3
12 = 1 * 1 * 2 * 2 * 3
16 = 1 * 2 * 2 * 2 * 2
4 = 1 * 1 * 1 * 1 * 1 * 4
6 = 1 * 1 * 1 * 1 * 2 * 3
8 = 1 * 1 * 1 * 2 * 2 * 2
3 = 1 * 1 * 1 * 1 * 1 * 1 * 3
4 = 1 * 1 * 1 * 1 * 1 * 2 * 2
2 = 1 * 1 * 1 * 1 * 1 * 1 * 1 * 2
1 = 1 * 1 * 1 * 1 * 1 * 1 * 1 * 1 * 1

Sampled (Underfoot)

by in Mathematics, Puzzles, Statistics and tagged , , , , , , , , , , | Leave a comment

Some interesting statistics from the American sociologist Elizabeth Wrigley-Field:

Here are three puzzles.

• American fertility fluctuated dramatically in the decades surrounding the Second World War. Parents created the smallest families during the Great Depression, and the largest families during the postwar Baby Boom. Yet children born during the Great Depression came from larger families than those born during the Baby Boom. How can this be?

• About half of the prisoners released in any given year in the United States will end up back in prison within five years. Yet the proportion of prisoners ever released who will ever end up back in prison, over their whole lifetime, is just one third. How can this be?
​
• People whose cancers are caught early by random screening often live longer than those whose cancers are detected later, after they are symptomatic. Yet those same random screenings might not save any lives. How can this be?

And here is a twist: these are all the same puzzle.

• Answers here: Length-Biased Sampling by Elizabeth Wrigley-Field

Proxi-Performative Post-Scriptum

The title of this post is, of course, a radical reference to core Led Zeppelin track “Trampled Underfoot” (1975).

Dime Time

by in Geometry, Mathematics and tagged , , , , , , , , , , , , , , , , , , , , | Leave a comment

Everyone knows the shapes for one and two dimensions, far fewer know the shapes for three and four dimensions, let alone five, six and seven. And what shapes are those? The shapes that answer this question:

• How many equidistant points are possible in 1d, 2d, 3d, 4d…?

In one dimension it’s obvious that the answer is 2. In other words, you can get only two equidistant points, (a,b), on a straight line. Point a must be as far from point b as point b is from point a. You can’t add a third point, c, such that (a,b,c) are equidistant. Not on a straight line in 1d. But suppose you bend the line into a circle, so that you’re working in two dimensions. It’s easy to place three equidistant points, (a,b,c), on a circle.

equidistant points on a circle

Three equidistant points around a circle forming the vertices of an equilateral triangle

And it’s also easy to see that the three points will form the vertices of an equilateral triangle. Now try adding a fourth point, d. If you place it in the center of the triangle, it will be equidistant from (a,b,c), but it will be nearer to (a,b,c) than they are to each other. So you can have only 2 equidistant points in 1d and 3 equidistant points in 2d.

But what are the co-ordinates of the equidistant points in 1d and 2d? Suppose (a,b) in 1d are given the co-ordinates (0) and (1), so that a is 1 unit distant from b. When you move to 2d and add point c, the co-ordinates for (a,b) become (0,0) and (1,0). They’re still 1 unit distant from each other. But what are the co-ordinates for c? Start by placing c exactly midway between a and b, so that it has the co-ordinates (0.5,0) and is 0.5 units distant from both a and b. Now, if you move c in the first dimension, it will become nearer either to a or b: (0.49,0) or (0.51,0) or (0.48,0) or (0.52,0)…

But if you move c in the second dimension, it will always be equidistant from a and b, because (a,b) stay in the first dimension, as it were, and c moves equally away from both into the second dimension. So where in 2d will c be 1 unit distant from both a and b just as a and b are 1 unit distant from each other in 1d? You can see the answer here:

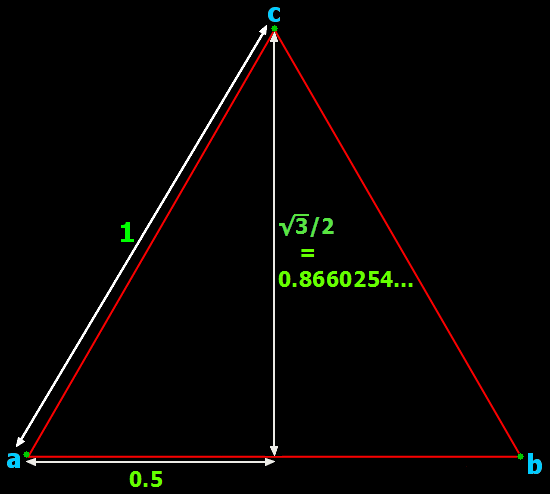equilateral_triangle heightHeight of an equilateral triangle

The co-ordinates for c are (0.5,√3/2) or (0.5,0.8660254…), because the second co-ordinate satisfies the Pythagorean equation 1^2 = 0.5^2 + (√3/2)^2 = 0.25 + 0.75. That is, to find the second co-ordinate of c for 2d, you find the answer to √(1 – 0.5^2) = √(1-0.25) = √0.75 = √(3/4) = √3/2 = 0.8660254….

But you can’t add a fourth point, d, in 2d such that (a,b,c,d) are equidistant. So let’s move to 3d for the points (a,b,c,d). Begin with point d in the center of the triangle formed by (a,b,c), where it will have the co-ordinates (0.5,√3/6,0) = (0.5,0.28867513…,0) and will be equidistant from (a,b,c). But d will be nearer to (a,b,c) than they are to each other. However, if you move d in the third dimension, it will be moving equally away from (a,b,c). So where in 3d will d be 1 unit from (a,b,c)? By analogy with 2d, the third co-ordinate for d will satisfy the generalized Pythagorean equation √(1 – 0.5^2 – (√3/6)^2). And √6/3 = √(1 – 0.5^2 – (√3/6)^2) = 0.81649658… So point d will have the co-ordinates (0.5,√3/6,√6/3) = (0.5, 0.288675135…, 0.816496581…).

And the four points (a,b,c,d) will be the vertices of a three-dimensional shape called the tetrahedron:

Rotating tetrahedron

Rotating tetrahedron

But you can’t add a fifth point, e, in 3d such that (a,b,c,d,e) are equidistant. So let’s move to 4d, the fourth dimension, for the points (a,b,c,d,e). Begin with point e in the center of the tetrahedron formed by (a,b,c,d), where it will have the co-ordinates (0.5,√3/6,√6/12,0) = (0.5,0.28867513…, 0.2041241…, 0) and will be equidistant from (a,b,c,d). But e will be nearer to (a,b,c,d) than they are to each other. However, if you move e in the fourth dimension, it will be moving equally away from (a,b,c,e). So where in 4d will e be 1 unit from (a,b,c,d)? By analogy with 2d and 3d, the co-ordinate for 4d will satisfy the equation √(1 – 0.5^2 – (√3/6)^2 – (√6/12)^2). And √10/4 = √(1 – 0.5^2 – (√3/6)^2 – (√6/12)^2) = 0.79056941… So point e will have the co-ordinates (0.5,√3/6,√6/3,√10/4) = (0.5, 0.288675135…, 0.816496581…, 0.79056941…).

And the five points (a,b,c,d,e) will be the vertices of a four-dimensional shape called variously the hyperpyramid, the 5-cell, the pentachoron, the 4-simplex, the pentatope, the pentahedroid and the tetrahedral pyramid. It’s impossible for 3d creatures like human beings (at present) to visualize the hyperpyramid, but we can see its 3d shadow, as it were. And here is the 3d shadow of a rotating hyperpyramid:

Rotating hyperpyramid or 5-cell

Rotating hyperpyramid

N.B. Wikipedia reveals the mathematically beautiful fact that the “simplest set of coordinates [for a hyperpyramid] is: (2,0,0,0), (0,2,0,0), (0,0,2,0), (0,0,0,2), (φ,φ,φ,φ), with edge length 2√2, where φ is the golden ratio.”

So that’s the hyperpyramid, with 5 points in 4d. But you can’t add a sixth point, f, in 4d such that (a,b,c,d,e,f) are equidistant. You have to move to 5d. And it should be clear by now that in any dimension nd, the maximum possible number of equidistant points, p, in that dimension will be p = n+1. And here are the co-ordinates for p in dimensions 1 to 10 (the co-ordinates are given in full for 1d to 4d, then for 5d to 10d only the co-ordinates of the additional point are given):

d1: (0), (1)
d2: (0,0), (1,0), (0.5,0.866025404)
d3: (0,0,0), (1,0,0), (0.5,0.866025404,0), (0.5,0.288675135,0.816496581)
d4: 0.5, 0.288675135, 0.204124145, 0.790569415
d5: 0.5, 0.288675135, 0.204124145, 0.158113883, 0.774596669
d6: 0.5, 0.288675135, 0.204124145, 0.158113883, 0.129099445, 0.763762616
d7: 0.5, 0.288675135, 0.204124145, 0.158113883, 0.129099445, 0.109108945, 0.755928946
d8: 0.5, 0.288675135, 0.204124145, 0.158113883, 0.129099445, 0.109108945, 0.0944911183, 0.75
d9: 0.5, 0.288675135, 0.204124145, 0.158113883, 0.129099445, 0.109108945, 0.0944911183, 0.0833333333, 0.745355992
d10: 0.5, 0.288675135, 0.204124145, 0.158113883, 0.129099445, 0.109108945, 0.0944911183, 0.0833333333, 0.0745355992, 0.741619849

In each dimension d, the final co-ordinate, cd+1, of the additional point satisfies the generalized Pythagorean equation cd+1 = √(1 – c1^2 – c2^2 – … cd^2).

Readers’ advisory: I am not a mathematician and the discussion above cannot be trusted to be free of errors, whether major or minor.