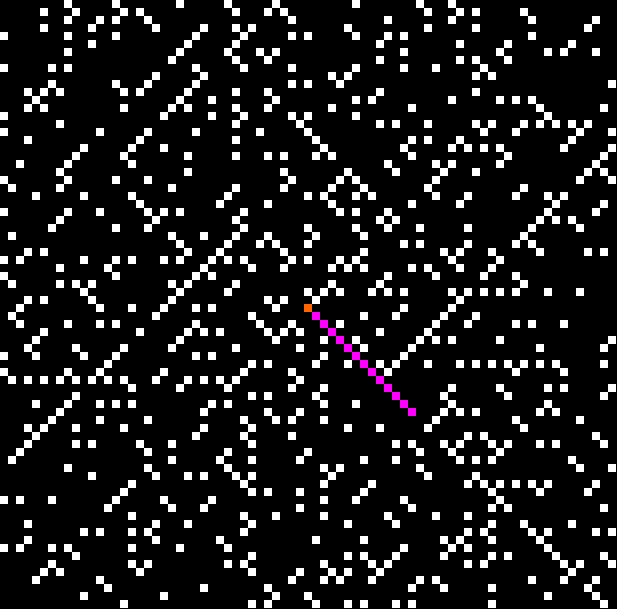
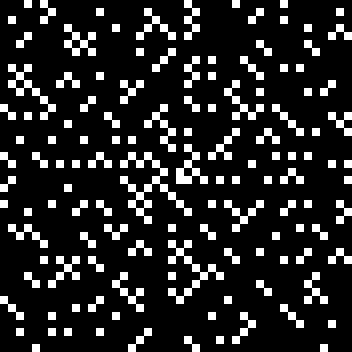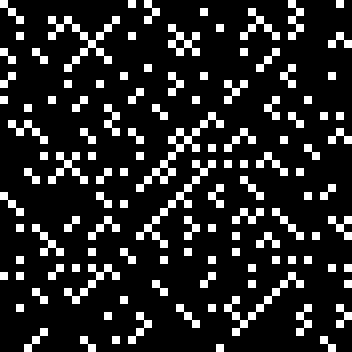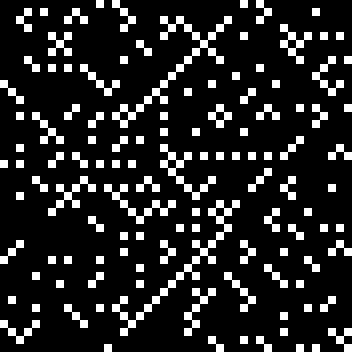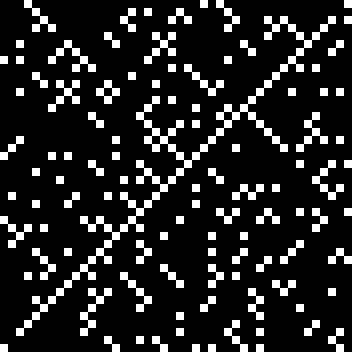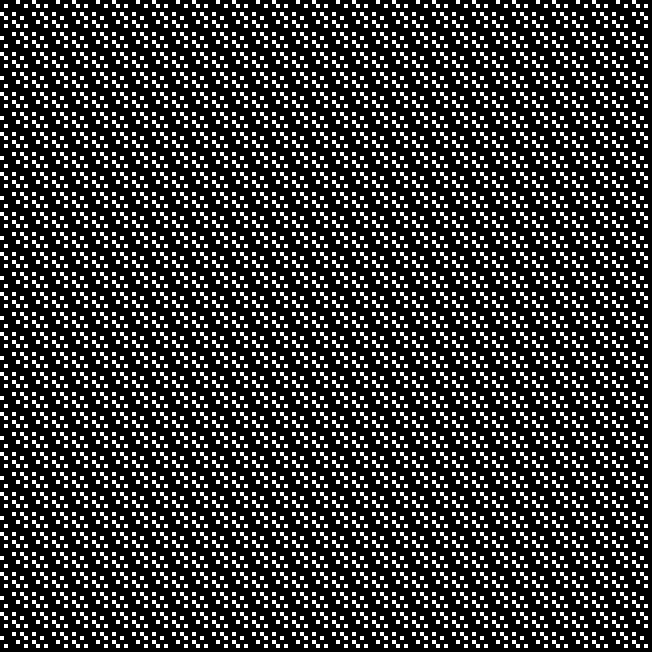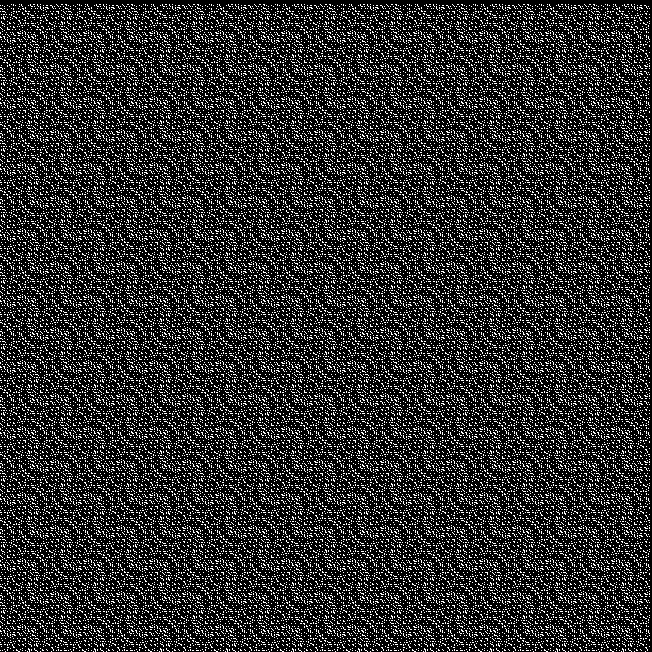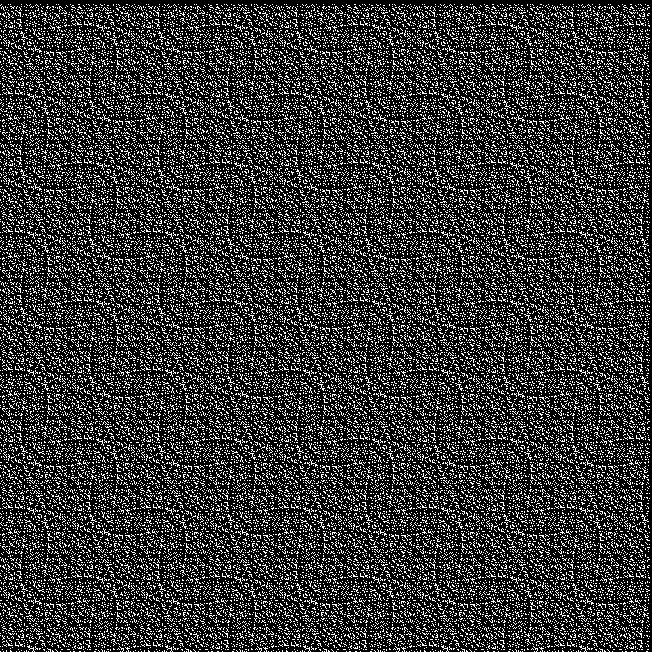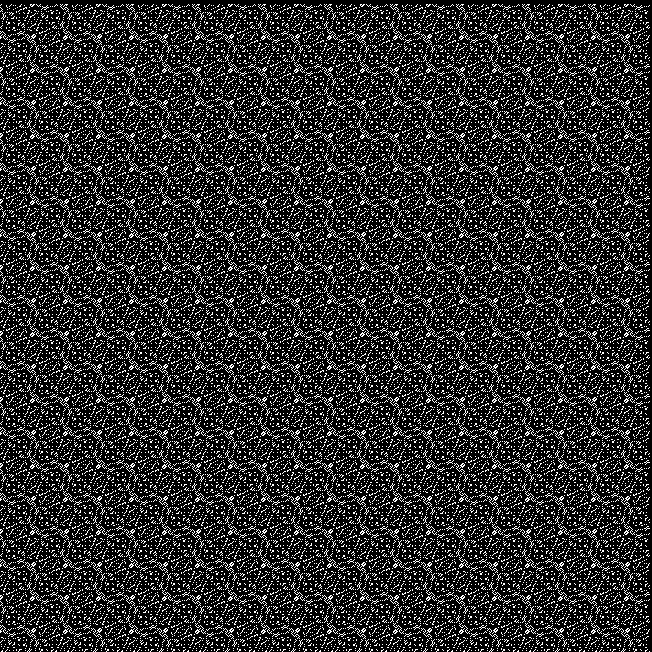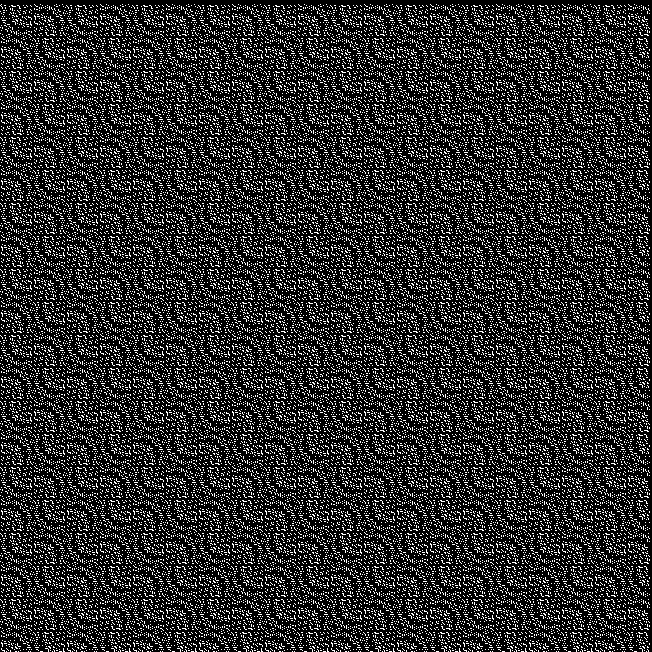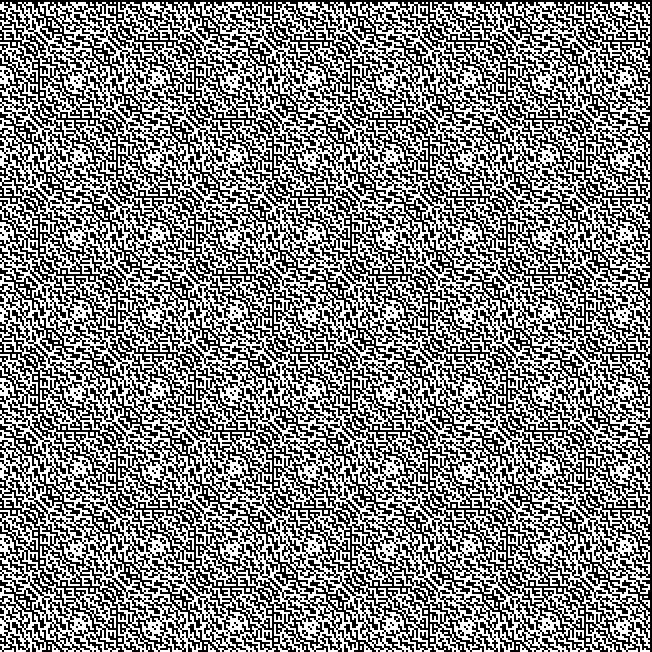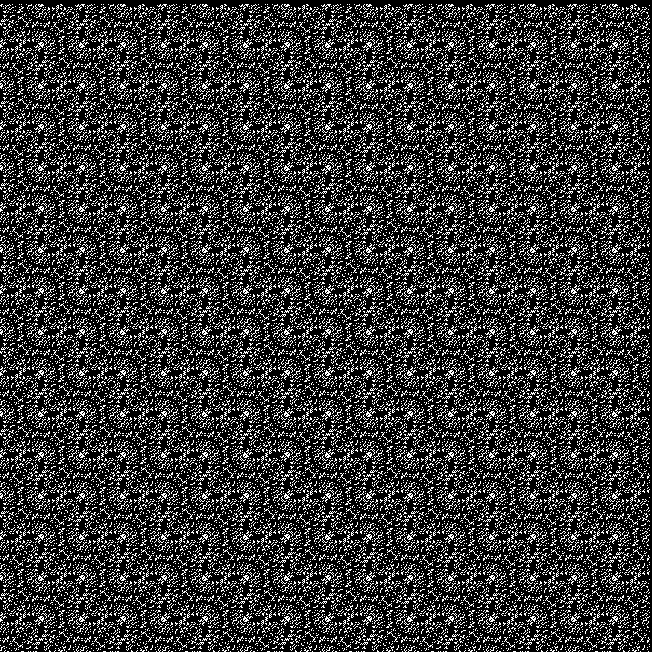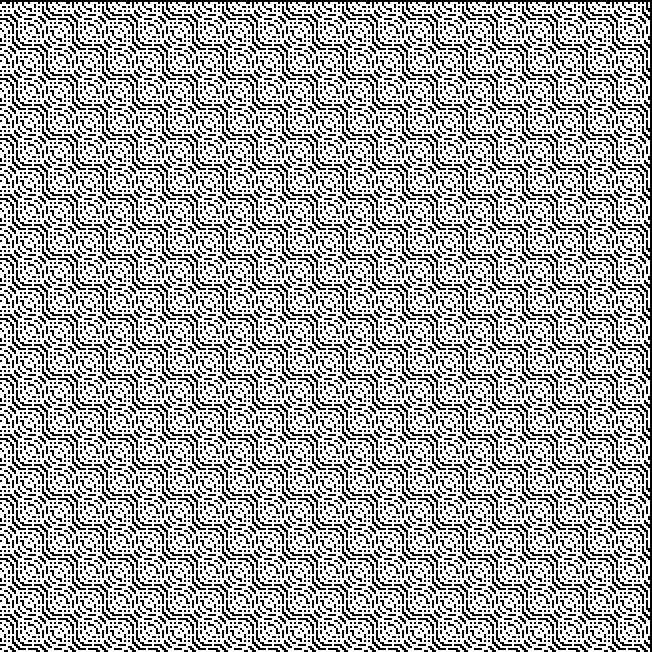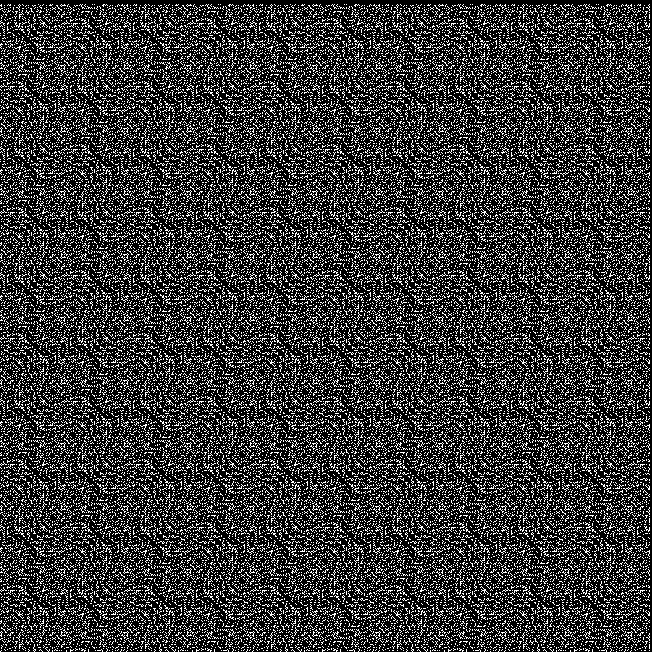The Sumber of the B’s

First a bit of a boredom. Then a bit of beauty. These are the triangular numbers, including 666, the Number of the Beast:

1, 3, 6, 10, 15, 21, 28, 36, 45, 55, 66, 78, 91, 105, 120, 136, 153, 171, 190, 210, 231, 253, 276, 300, 325, 351, 378, 406, 435, 465, 496, 528, 561, 595, 630, 666, 703, 741, 780, 820, 861, 903, 946, 990, 1035, 1081, 1128, 1176, 1225, 1275, …

You can createthem as sumbers, that is, as numbers made by summing the whole numbers:

tri(1) = 1 = 1
tri(2) = 3 = 2+1
tri(3) = 6 = 3+2+1
tri(4) = 10 = 4+3+2+1
tri(5) = 15 = 5+4+3+2+1
tri(6) = 21 = 6+5+4+3+2+1
tri(7) = 28 = 7+6+5+4+3+2+1
tri(8) = 36 = 8+7+6+5+4+3+2+1
tri(9) = 45 = 9+8+7+6+5+4+3+2+1
tri(10) = 55 = 10+9+8+7+6+5+4+3+2+1

And here are the square numbers:

1, 4, 9, 16, 25, 36, 49, 64, 81, 100, 121, 144, 169, 196, 225, 256, 289, 324, 361, 400, 441, 484, 529, 576, 625, 676, 729, 784, 841, 900, 961, 1024, 1089, 1156, 1225, 1296, 1369, 1444, 1521, 1600, 1681, 1764, 1849, 1936, 2025, 2116, 2209, 2304, 2401, 2500, …

You can create square numbers in various ways. Most obviously, by multiplying each whole number by itself:

sq(1) = 1*1 = 1
sq(2) = 2*2 = 4
sq(3) = 3*3 = 9
sq(4) = 4*4 = 16
sq(5) = 5*5 = 25
sq(6) = 6*6 = 36
sq(7) = 7*7 = 49
sq(8) = 8*8 = 64
sq(9) = 9*9 = 81
sq(10) = 10*10 = 100

Less obviously, by summing consecutive odd numbers:

sq(1) = 1 = 1
sq(2) = 1+3 = 4
sq(3) = 1+3+5 = 9
sq(4) = 1+3+5+7 = 16
sq(5) = 1+3+5+7+9 = 25
sq(6) = 1+3+5+7+9+11 = 36
sq(7) = 1+3+5+7+9+11+13 = 49
sq(8) = 1+3+5+7+9+11+13+15 = 64
sq(9) = 1+3+5+7+9+11+13+15+17 = 81
sq(10) = 1+3+5+7+9+11+13+15+17+19 = 100

And by summing pairs of consecutive triangular numbers (note that tri(0) = 0):

sq(1) = tri(0) + tri(1) = 0 + 1 = 1
sq(2) = tri(1) + tri(2) = 1 + 3 = 4
sq(3) = tri(2) + tri(3) = 3 + 6 = 9
sq(4) = tri(3) + tri(4) = 6 + 10 = 16
sq(5) = tri(4) + tri(5) = 10 + 15 = 25
sq(6) = tri(5) + tri(6) = 15 + 21 = 36
sq(7) = tri(6) + tri(7) = 21 + 28 = 49
sq(8) = tri(7) + tri(8) = 28 + 36 = 64
sq(9) = tri(8) + tri(9) = 36 + 45 = 81
sq(10) = tri(9) + tri(10) = 45 + 55 = 100

But sometimes squares are the sum of two triangular numbers that aren’t consecutive:

sq(4) = tri(1) + tri(5) = 1+15 = 16
sq(9) = tri(2) + tri(12) = 3+78 = 81
sq(16) = tri(2) + tri(22) = 3+253 = 256
sq(52) = tri(2) + tri(73) = 3+2701 = 2704
sq(14) = tri(3) + tri(19) = 6+190 = 196
sq(21) = tri(3) + tri(29) = 6+435 = 441
sq(44) = tri(9) + tri(61) = 45+1891 = 1936
sq(51) = tri(9) + tri(71) = 45+2556 = 2601
sq(49) = tri(10) + tri(68) = 55+2346 = 2401
sq(56) = tri(10) + tri(78) = 55+3081 = 3136
sq(16) = tri(11) + tri(19) = 66+190 = 256
sq(38) = tri(11) + tri(52) = 66+1378 = 1444
sq(54) = tri(11) + tri(75) = 66+2850 = 2916
sq(87) = tri(47) + tri(113) = 1128+6441 = 7569
sq(77) = tri(48) + tri(97) = 1176+4753 = 5929
sq(121) = tri(64) + tri(158) = 2080+12561 = 14641
sq(141) = tri(96) + tri(174) = 4656+15225 = 19881
sq(121) = tri(100) + tri(138) = 5050+9591 = 14641

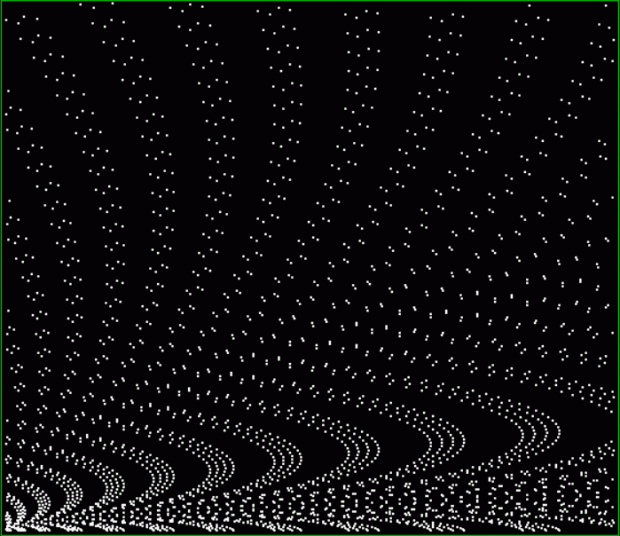
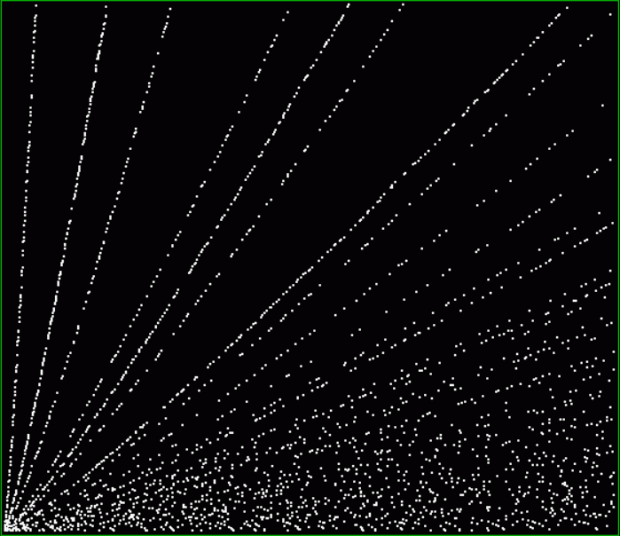
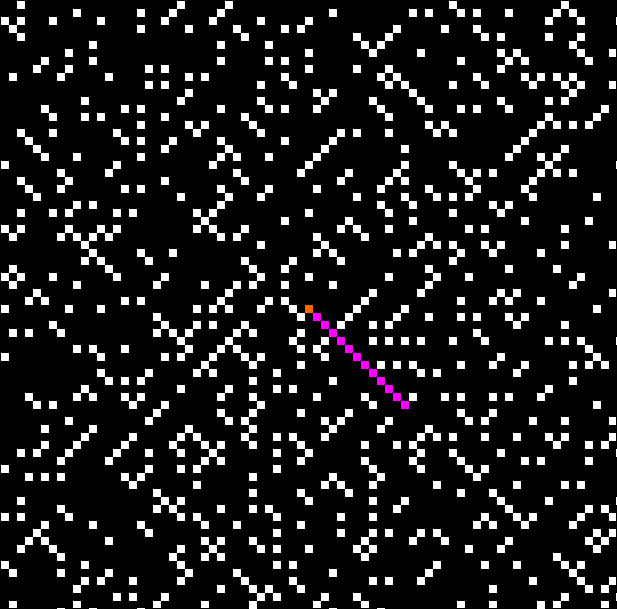
Here’s a graph of squares that are the sum of any two triangular numbers, that is, is_square(tri(k1)+tri(k2)). The x axis is 1..k1 and the y axis is 1..k2, so the graph is symmetrical:

tri(k1) + tri(k2) = square(k3)

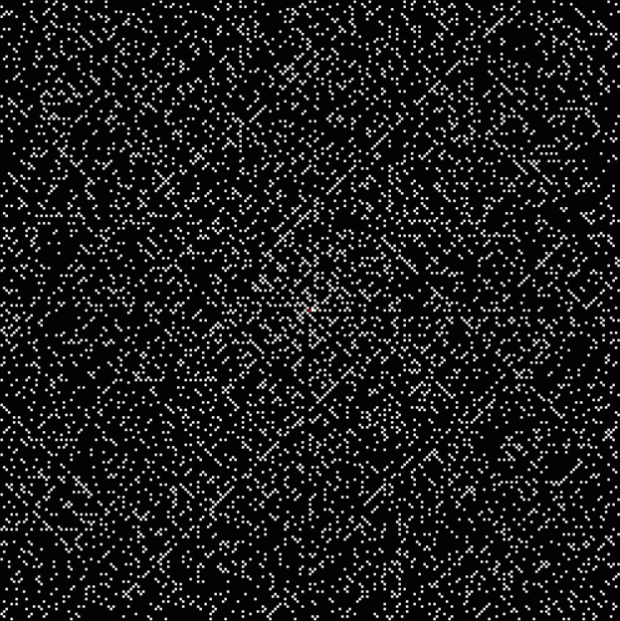
The (double) line at 45° represents squares that are the sum of consecutive triangulars. Other lines represent similarly regular patterns. Now for a bit of beauty. Things get more visually interesting when you test for squares that are the sums of any integer and a triangular number:

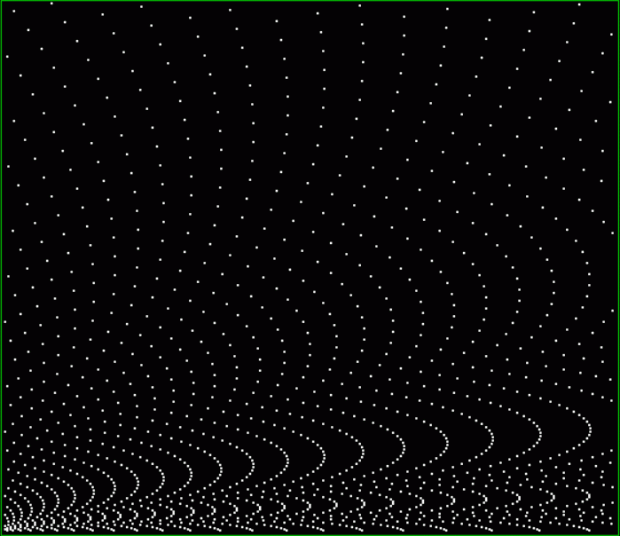
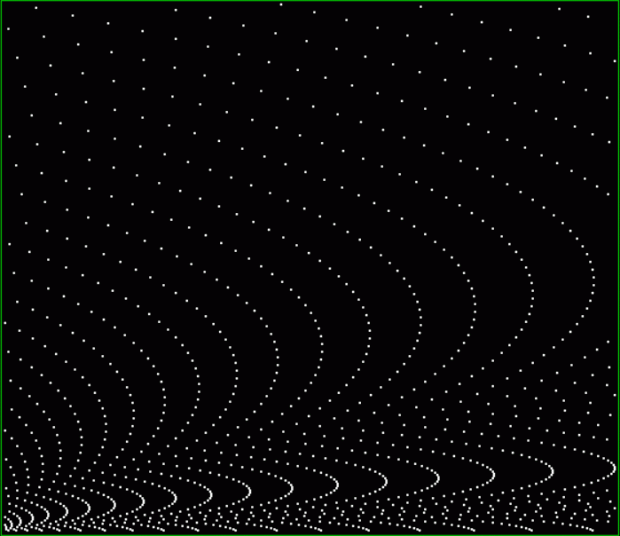
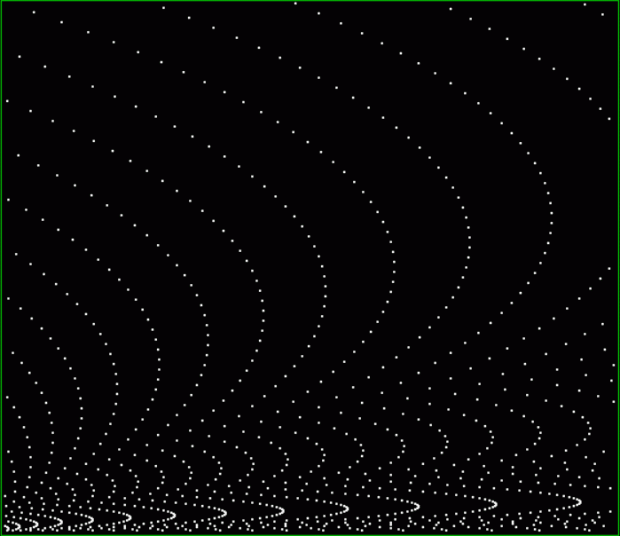
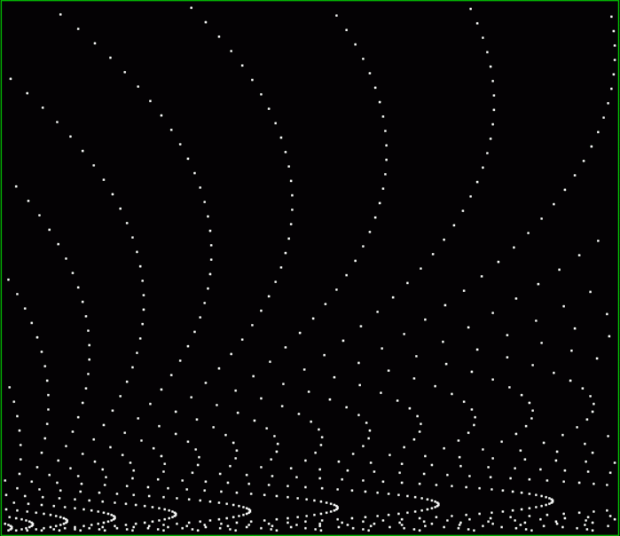
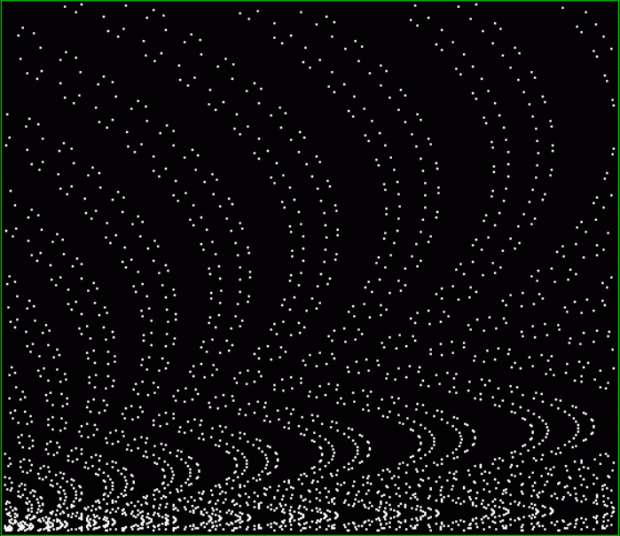
k1 + tri(k2) = square(k3)

The curves are optical oddities: where do they begin and end? The upper ones become lost to the eye in the lower ones. And vice versa. But you can force your eye to trace them further that it wants to.

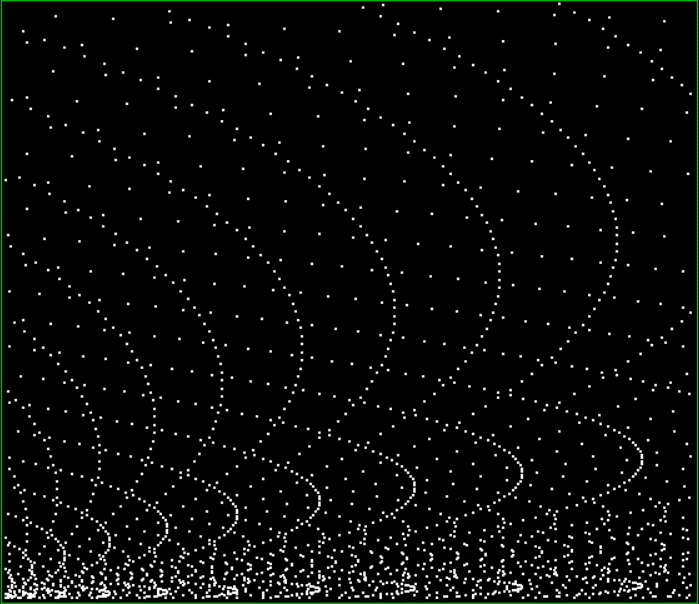
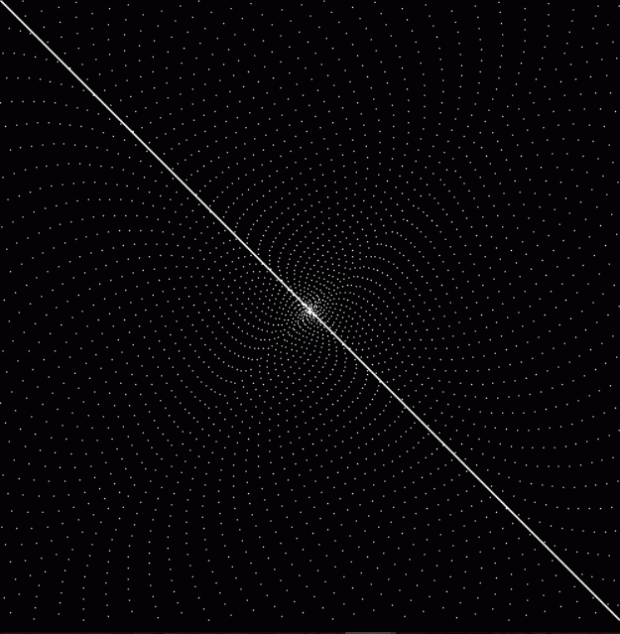
Now try sums of integers and other polygonal numbers:

k1 + tri(k2) = pentagonal(k3)

k1 + square(k2) = pentagonal(k3)

k1 + pentagonal(k2) = square(k3)

k1 + hexagonal(k2) = pentagonal(k3)

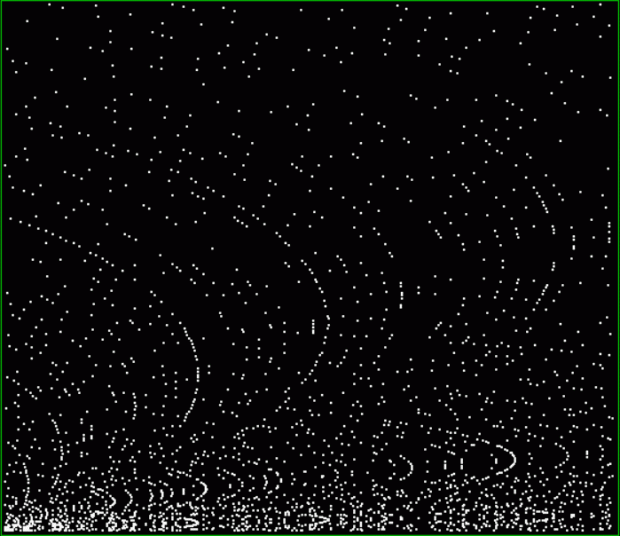
And try other number sequences, like multiples of 4 with polygonals:

k1*4 + pentagonal(k2) = tri(k3)

k1*4 + square(k2) = tri(k3)

k1*4 + heptagonal(k2) = tri(k3)

And primes with polygonals:

tri(k1) + prime(k2) = tri(k3)

prime(k1) + tri(k2) = square(k3)

prime(k1) + octagonal(k2) = square(k3)

prime(k1) + pentagonal(k2) = square(k3)

prime(k1) + square(k2) = decagonal(k3)

prime(k1) + tri(k2) = hendecagonal(k3)

Abounding in Abundants

Tuesday, 19th Nov, 2024 by Krilling for Company in Arithmetic, Integer Sequences, Mathematics, Prime numbers and tagged abundant numbers, Carolus Bovillus, Charles de Bovelles, David Wells, deficient numbers, OEIS, Online Encyclopedia of Integer Sequences, Penguin Dictionary of Curious and Interesting Numbers, perfect numbers, prime numbers, recreational math, recreational mathematics, recreational maths, Stanislaw Ulam, sum of divisors, sum of factors, Ulam Spirals | Leave a comment

This is the famous Ulam spiral, invented by the Jewish mathematician Stanisław Ulam (pronounced OO-lam) to represent prime numbers on a square grid:

The Ulam spiral of prime numbers

The red square represents 1, with 2 as the white block immediately to its right and 3 immediately above 2. Then 5 is the white block one space to the left of 3 and 7 the white block one space below 5. Then 11 is the white block right beside 2 and 13 the white block one space above 11. And so on. The primes aren’t regularly spaced on the spiral but patterns are nevertheless appearing. Here’s the Ulam spiral at higher resolutions:

The Ulam spiral x2

The Ulam spiral x4

The primes are neither regular nor random in their distribution on the spiral. They stand tantalizingly betwixt and between. So the numbers represented on this Ulam-like spiral, which looks like an aerial view of a city designed by architects who occasionally get drunk:

Ulam-like spiral of abundant numbers

The distribution of abundant numbers is much more regular than the primes, but is far from wholly predictable. And what are abundant numbers? They’re numbers n such that sum(divisors(n)-n) > n. In other words, when you add the divisors of n less than n, the sum is greater than n. The first abundant number is 12:

12 is divisible by 1, 2, 3, 4, 6 → 1 + 2 + 3 + 4 + 6 = 16 > 12

The abundant numbers go like this:

12, 18, 20, 24, 30, 36, 40, 42, 48, 54, 56, 60, 66, 70, 72, 78, 80, 84, 88, 90, 96, 100, 102, 104, 108, 112, 114, 120, 126, 132, 138, 140, 144, 150, 156, 160, 162, 168, 174, 176, 180, 186, 192, 196, 198, 200, 204, 208, 210, 216, 220, 222, 224, 228, 234, 240, 246, 252, 258, 260, 264, 270… — A005101 at the Online Encyclopedia of Integer Sequences

Are all abundant numbers even? No, but the first odd abundant number takes a long time to arrive: it’s 45045. The abundance of 45045 was first discovered by the French mathematician Charles de Bovelles or Carolus Bovillus (c. 1475-1566), according to David Wells in his wonderful Penguin Dictionary of Curious and Interesting Numbers (1986):

45045 = 3^2 * 5 * 7 * 11 * 13 → 1 + 3 + 5 + 7 + 9 + 11 + 13 + 15 + 21 + 33 + 35 + 39 + 45 + 55 + 63 + 65 + 77 + 91 + 99 + 105 + 117 + 143 + 165 + 195 + 231 + 273 + 315 + 385 + 429 + 455 + 495 + 585 + 693 + 715 + 819 + 1001 + 1155 + 1287 + 1365 + 2145 + 3003 + 3465 + 4095 + 5005 + 6435 + 9009 + 15015 = 59787 > 45045

Here’s the spiral of abundant numbers at higher resolutions:

Abundant numbers x2

Abundant numbers x4

Negating the spiral of the abundant numbers — almost — is the spiral of the deficient numbers, where sum(divisors(n)-n) < n. Like most odd numbers, 15 is deficient:

15 = 3 * 5 → 1 + 3 + 5 = 9 < 15

Here’s the spiral of deficient numbers at various resolutions:

Deficient numbers on Ulam-like spiral

Deficient numbers x2

Deficient numbers x4

The spiral of deficient numbers doesn’t quite negate (reverse the colors of) the spiral of abundant numbers because of the very rare perfect numbers, where sum(divisors(n)-n) = n. That is, their factor-sums are exactly equal to themselves:

• 6 = 2 * 3 → 1 + 2 + 3 = 6
• 28 = 2^2 * 7 → 1 + 2 + 4 + 7 + 14 = 28
• 496 = 2^4 * 31 → 1 + 2 + 4 + 8 + 16 + 31 + 62 + 124 + 248 = 496

Now let’s try numbers n such than sum(divisors(n)) mod 2 = 1 (“n mod 2″ gives the remainder when n is divided by 2, i.e. n mod 2 is either 0 or 1). For example:

• 4 = 2^2 → 1 + 2 + 4 = 7 → 7 mod 2 = 1
• 18 = 2 * 3^2 → 1 + 2 + 3 + 6 + 9 + 18 = 39 → 39 mod 2 = 1
• 72 = 2^3 * 3^2 → 1 + 2 + 3 + 4 + 6 + 8 + 9 + 12 + 18 + 24 + 36 + 72 = 195 → 195 mod 2 = 1

Here are spirals for these numbers:

Ulam-like spiral for n such than sum(divisors(n)) mod 2 = 1

sum(divisors(n)) mod 2 = 1 x2

sum(divisors(n)) mod 2 = 1 x4

sum(divisors(n)) mod 2 = 1 x8

sum(divisors(n)) mod 2 = 1 x16

Period Panes

Friday, 29th Dec, 2023 by Krilling for Company in Arithmetic, Base Behavior, Circles, Geometry, Mathematics, Reciprocals and tagged 1/7, 142857, 29, 7, animated gifs, Arithmetic, Circles, David Wells, maximum period, maximum period prime reciprocals, Penguin Dictionary of Curious and Interesting Numbers, period of 1/7, prime numbers, prime reciprocals, primes, reciprocal of 7, reciprocals, recreational math, recreational mathematics, recreational maths, remainders, remainders of 1/7 | Leave a comment

In his Penguin Dictionary of Curious and Interesting Numbers (1986), David Wells says that 142857 is “beloved of all recreational mathematicians”. He then says it’s the decimal period of the reciprocal of the fourth prime: “1/7 = 0·142857142857142…” And the reciprocal has maximum period. There are 6 = 7-1 digits before repetition begins, unlike the earlier prime reciprocals:

1/2 = 0·5 1/3 = 0·333... 1/5 = 0·2 1/7 = 0·142857 142857 142...

In other words, all possible remainders appear when you calculate the decimals of 1/7:

1*10 / 7 = 1 remainder 3 → 0·1 3*10 / 7 = 4 remainder 2 → 0·14 2*10 / 7 = 2 remainder 6 → 0·142 6*10 / 7 = 8 remainder 4 → 0·1428 4*10 / 7 = 5 remainder 5 → 0·14285 5*10 / 7 = 7 remainder 1 → 0·142857 1*10 / 7 = 1 remainder 3 → 0·142857 1 3*10 / 7 = 4 remainder 2 → 0·142857 14 2*10 / 7 = 2 remainder 6 → 0·142857 142...

That happens again with 1/17 and 1/19, but Wells says that “surprisingly, there is no known method of predicting which primes have maximum period.” It’s a simple question that involves some deep mathematics. Looking at prime reciprocals is like peering through a small window into a big room. Some things are easy to see, some are difficult and some are presently impossible.

In his discussion of 142857, Wells mentions one way of peering through a period pane: “The sequence of digits also makes a striking pattern when the digits are arranged around a circle.” Here is the pattern, with ten points around the circle representing the digits 0 to 9:

The digits of 1/7 = 0·142857142…

But I prefer, for further peers through the period-panes, to create the period-panes using remainders rather than digits. That is, the number of points around the circle is determined by the prime itself rather than the base in which the reciprocal is calculated:

The remainders of 1/7 = 1, 3, 2, 6, 4, 5…

Period-panes can look like butterflies or bats or bivalves or spiders or crabs or even angels. Try the remainders of 1/13. This prime reciprocal doesn’t have maximum period: 1/13 = 0·076923 076923 076923… So there are only six remainders, creating this pattern:

remainders(1/13) = 1, 10, 9, 12, 3, 4

The multiple 2/13 has different remainders and creates a different pattern:

remainders(2/13) = 2, 7, 5, 11, 6, 8

But 1/17, 1/19 and 1/23 all have maximum period and yield these period-panes:

remainders(1/17) = 1, 10, 15, 14, 4, 6, 9, 5, 16, 7, 2, 3, 13, 11, 8, 12

remainders(1/19) = 1, 10, 5, 12, 6, 3, 11, 15, 17, 18, 9, 14, 7, 13, 16, 8, 4, 2

remainders(1/23) = 1, 10, 8, 11, 18, 19, 6, 14, 2, 20, 16, 22, 13, 15, 12, 5, 4, 17, 9, 21, 3, 7

It gets mixed again with the prime 73, which doesn’t have maximum period and yields a plethora of period-panes (some patterns repeat with different n * 1/73, so I haven’t included them):

remainders(1/73)

remainders(2/73)

remainders(3/73)

remainders(4/73)

remainders(5/73)

remainders(6/73)

remainders(9/73)

remainders(11/73) (identical to pattern of 5/73)

remainders(12/73)

remainders(18/73)

101 yields a plethora of period-panes, but they’re variations on a simple theme. They look like flapping wings in this animated gif:

remainders of n/101 (animated)

The remainders of 137 yield more complex period-panes:

remainders of n/137 (animated)

And what about different bases? Here are period-panes for the remainders of 1/17 in bases 2 to 16:

remainders(1/17) in base 2

remainders(1/17) in b3

remainders(1/17) in b4

remainders(1/17) in b5

remainders(1/17) in b6

remainders(1/17) in b7

remainders(1/17) in b8

remainders(1/17) in b9

remainders(1/17) in b10

remainders(1/17) in b11

remainders(1/17) in b12

remainders(1/17) in b13

remainders(1/17) in b14

remainders(1/17) in b15

remainders(1/17) in b16

remainders(1/17) in bases 2 to 16 (animated)

But the period-panes so far have given a false impression. They’ve all been symmetrical. That isn’t the case with all the period-panes of n/19:

remainders(1/19) in b2

remainders(1/19) in b3

remainders(1/19) in b4 = 1, 4, 16, 7, 9, 17, 11, 6, 5 (asymmetrical)

remainders(1/19) in b5 = 1, 5, 6, 11, 17, 9, 7, 16, 4 (identical pattern to that of b4)

remainders(1/19) in b6

remainders(1/19) in b7

remainders(1/19) in b8

remainders(1/19) in b9

remainders(1/19) in b10 (identical pattern to that of b2)

remainders(1/19) in b11

remainders(1/19) in b12

remainders(1/19) in b13

remainders(1/19) in b14

remainders(1/19) in b15

remainders(1/19) in b16

remainders(1/19) in b17

remainders(1/19) in b18

remainders(1/19) in bases 2 to 18 (animated)

Here are a few more period-panes in different bases:

remainders(1/11) in b2

remainders(1/11) in b7

remainders(1/13) in b6

remainders(1/43) in b6

remainders in b2 for reciprocals of 29, 37, 53, 59, 61, 67, 83, 101, 107, 131, 139, 149 (animated)

And finally, to performativize the pun of “period pane”, here are some period-panes for 1/29, whose maximum period will be 28 (NASA says that the “Moon takes about one month to orbit Earth … 27.3 days to complete a revolution, but 29.5 days to change from New Moon to New Moon”):

remainders(1/29) in b4

remainders(1/29) in b5

remainders(1/29) in b8

remainders(1/29) in b9

remainders(1/29) in b11

remainders(1/29) in b13

remainders(1/29) in b14

remainders(1/29) in various bases (animated)

Prime Times

Saturday, 11th Dec, 2021 by Krilling for Company in Integer Sequences, Mathematics, Prime numbers and tagged A005234, math, mathematics, maths, OEIS, Online Encylopedia of Integer Sequences, prime numbers, primes, primorials, recreational math, recreational mathematics, recreational maths | Leave a comment

The factorial of an integer is equal to that that integer multiplied by all the integers smaller than it. For example, this is factorial(7) or 7!:
7! = 7 * 6 * 5 * 4 * 3 * 2 * 1 = 5040
The primorial of a prime is equal to that that prime multiplied by all the primes smaller than it. For example, this is primorial(7):
primorial(7) = 7 * 5 * 3 * 2 = 210 = 4# (the product of the first four primes)
Here’s an interesting set of primorials incremented-by-one:
primorial(2) + 1 = 2 + 1 = 3 (prime) primorial(3) + 1 = 2*3 + 1 = 7 (prime) primorial(5) + 1 = 2*3*5 + 1 = 31 (prime) primorial(7) + 1 = 2*3*5*7 + 1 = 211 (prime) primorial(11) + 1 = 2*3*5*7*11 + 1 = 2311 (prime) primorial(31) + 1 = 2*3*5*7*11*13*17*19*23*29*31 + 1 = 200560490131 (prime) primorial(379) + 1 = 1,719,620,105,458,406,433,483,340,568,317,543,019,584,575,635,895,742,560,438,771,105,058,321,655,238,562,613,083,979,651,479,555,788,009,994,557,822,024,565,226,932,906,295,208,262,756,822,275,663,694,111 (prime) primorial(1019) + 1 = 20,404,068,993,016,374,194,542,464,172,774,607,695,659,797,117,423,121,913,227,131,032,339,026,169,175,929,902,244,453,757,410,468,728,842,929,862,271,605,567,818,821,685,490,676,661,985,389,839,958,622,802,465,986,881,376,139,404,138,376,153,096,103,140,834,665,563,646,740,160,279,755,212,317,501,356,863,003,638,612,390,661,668,406,235,422,311,783,742,390,510,526,587,257,026,500,302,696,834,793,248,526,734,305,801,634,165,948,702,506,367,176,701,233,298,064,616,663,553,716,975,429,048,751,575,597,150,417,381,063,934,255,689,124,486,029,492,908,966,644,747,931 (prime) primorial(1021) + 1 = 20,832,554,441,869,718,052,627,855,920,402,874,457,268,652,856,889,007,473,404,900,784,018,145,718,728,624,430,191,587,286,316,088,572,148,631,389,379,309,284,743,016,940,885,980,871,887,083,026,597,753,881,317,772,605,885,038,331,625,282,052,311,121,306,792,193,540,483,321,703,645,630,071,776,168,885,357,126,715,023,250,865,563,442,766,366,180,331,200,980,711,247,645,589,424,056,809,053,468,323,906,745,795,726,223,468,483,433,625,259,000,887,411,959,197,323,973,613,488,345,031,913,058,775,358,684,690,576,146,066,276,875,058,596,100,236,112,260,054,944,287,636,531 (prime) primorial(2657) + 1 = 78,244,737,296,323,701,708,091,142,569,062,680,832,012,147,734,404,650,078,590,391,114,054,859,290,061,421,837,516,998,655,549,776,972,299,461,276,876,623,748,922,539,131,984,799,803,433,363,562,299,977,701,808,549,255,204,262,920,151,723,624,296,938,777,341,738,751,806,450,993,015,446,712,522,509,989,316,673,420,506,749,359,414,629,957,842,716,112,900,306,643,009,542,215,969,000,431,330,219,583,111,410,996,807,066,475,261,560,303,182,609,636,056,108,367,412,324,508,444,341,178,028,289,201,803,518,093,842,982,877,662,621,552,756,279,669,241,303,362,152,895,160,479,720,040,128,335,518,247,125,849,521,099,841,272,983,588,935,580,888,630,036,283,712,163,901,558,436,498,481,482,160,712,530,124,868,714,141,094,634,892,999,056,865,426,200,254,647,241,979,548,935,087,621,308,526,547,138,125,987,102,062,688,568,486,250,939,447,065,798,353,626,745,169,380,579,442,233,006,898 ,444,700,264,240,321,482,823,859,842,044,524,114,576,784,795,294,818,755,525,169,192,652,108,755,230,262,128,210,258,672,754,900,845,837,728,345,782,457,465,793,874,408,469,588,052,577,208,643,754,019,053,756,394,151,041,512,099,598,925,557,724,343,099,264,685,155,934,891,439,161,866,250,113,047,185,553,511,797,406,764,115,907,248,713,405,817,594,729,550,600,082,808,324,331,387,143,679,800,355,356,811,873,430,669,962,333,651,282,822,030,473,702,042,073,141,618,450,021,084,993,659,382,646,598,194,115,178,864,433,545,186,250,667,775,794,249,961,932,761,063,071,117,967,553,887,984,011,652,643,245,393,971 (prime) primorial(3229) + 1 = 689,481,240,122,180,255,681,227,812,346,871,771,457,221,628,238,467,511,261,402,638,443,056,696,165,896,544,725,098,860,107,293,247,422,610,010,824,870,599,655,026,129,367,004,672,337,297,193,288,816,463,520,704,235,722,580,204,218,943,598,425,089,855,869,341,564,771,022,924,163,236,141,415,235,947,085,902,422,536,824,665,765,244,189,167,643,048,218,572,769,125,400,511,177,245,717,452,516,267,205,786,258,497,574,258,715,214,994,129,786,103,824,740,384,634,788,909,041,221,747,073,062,941,769,355,745,272,170,421,584,636,198,911,899,164,272,930,590,704,655,882,680,817,754,473,306,122,122,423,384,160,639,995,940,152,584,830,810,911,265,680,382,263,051,658,031,509,463,010,733,595,465,426,943,956,643,445,876,702,680,730,987,739,513,538,299,069,540,636,616,098,525,527,546,435,002,783,615,353,417,794,625,251,129,892,373,849,727,119,530,335,366,131,575,986,221,685,088,118,143,088,371,896,087,248,659,669,154,564,925,048,225,211,644,681,303,874,490,648,860,319,990,785,185,350,796,853,298,548,942,407,689,617,641,587,755,314,125,485,345,107,782,298,938,892,240,282,038,605,672,241,010,302,874,153,509,795,545,077,305,234,459,038,983,235,361,138,814,897,166,376,363,090,128,647,084,552,385,969,054,439,430,382,421,762,883,708,894,899,853,286,109,068,224,980,793,075,241,538,872,287,253,835,877,394,821,667,363,465,425,187,353,453,157,415,169,810,167,271,517,665,273,484,442,461,468,031,313,956,356,871,467,191,959,110,440,864,194,544,244,079,053,955,897,287,010,339,385,419,923,838,571,256,564,818,350,769,518,898,003,780,557,167,344,272,499,224,580,817,920,441,512,610,104,625,622,872,289,967,615,843,092,782,763,554,732,404,239,287,463,466,833,602,966,629,613,502,579,134,371,295,289,680,374,088,987,611,189,907,873,072,122,808,833,765,972,650,050,982,877,578,244,899,073,193,043,546,490,795,625,023,568,563,926,988,371 (prime)

Elsewhere Other-Accessible

• A005234 at the Online Encylopedia of Integer Sequences — “Primorial plus 1 primes: primes p such that 1 + product of primes up to p is prime”.

Period Panes

Wednesday, 7th Jul, 2021 by Krilling for Company in Base Behavior, Mathematics, Prime numbers, Reciprocals and tagged 1/n, David Wells, decimal reciprocals, math, mathematics, maths, maximum period prime reciprocals, maximum period reciprocals, Penguin Dictionary of Curious and Interesting Numbers, prime numbers, primes, recipro, recreational math, recreational mathematics, recreational maths | 2 Comments

In The Penguin Dictionary of Curious and Interesting Numbers (1987), David Wells remarks that 142857 is “a number beloved of all recreational mathematicians”. He then explains that it’s “the decimal period of 1/7: 1/7 = 0·142857142857142…” and “the first decimal reciprocal to have maximum period, that is, the length of its period is only one less than the number itself.”

Why does this happen? Because when you’re calculating 1/n, the remainders can only be less than n. In the case of 1/7, you get remainders for all integers less than 7, i.e. there are 6 distinct remainders and 6 = 7-1:
(1*10) / 7 = 1 remainder 3, therefore 1/7 = 0·1... (3*10) / 7 = 4 remainder 2, therefore 1/7 = 0·14... (2*10) / 7 = 2 remainder 6, therefore 1/7 = 0·142... (6*10) / 7 = 8 remainder 4, therefore 1/7 = 0·1428... (4*10) / 7 = 5 remainder 5, therefore 1/7 = 0·14285... (5*10) / 7 = 7 remainder 1, therefore 1/7 = 0·142857... (1*10) / 7 = 1 remainder 3, therefore 1/7 = 0·1428571... (3*10) / 7 = 4 remainder 2, therefore 1/7 = 0·14285714... (2*10) / 7 = 2 remainder 6, therefore 1/7 = 0·142857142...
Mathematicians know that reciprocals with maximum period can only be prime reciprocals and with a little effort you can work out whether a prime will yield a maximum period in a particular base. For example, 1/7 has maximum period in bases 3, 5, 10, 12 and 17:
1/21 = 0·010212010212010212... in base 3 1/12 = 0·032412032412032412... in base 5 1/7 = 0·142857142857142857... in base 10 1/7 = 0·186A35186A35186A35... in base 12 1/7 = 0·274E9C274E9C274E9C... in base 17
To see where else 1/7 has maximum period, have a look at this graph:

Period pane for primes 3..251 and bases 2..39

I call it a “period pane”, because it’s a kind of window into the behavior of prime reciprocals. But what is it, exactly? It’s a graph where the x-axis represents primes from 3 upward and the y-axis represents bases from 2 upward. The red squares along the bottom aren’t part of the graph proper, but indicate primes that first occur after a power of two: 5 after 4=2^2; 11 after 8=2^3; 17 after 16=2^4; 37 after 32=2^5; 67 after 64=2^6; and so on.

If a prime reciprocal has maximum period in a particular base, the graph has a solid colored square. Accordingly, the purple square at the bottom left represents 1/7 in base 10. And as though to signal the approval of the goddess of mathematics, the graph contains a lower-case b-for-base, which I’ve marked in green. Here are more period panes in higher resolution (open the images in a new window to see them more clearly):

Period pane for primes 3..587 and bases 2..77

Period pane for primes 3..1303 and bases 2..152

An interesting pattern has begun to appear: note the empty lanes, free of reciprocals with maximum period, that stretch horizontally across the period panes. These lanes are empty because there are no prime reciprocals with maximum period in square bases, that is, bases like 4, 9, 25 and 36, where 4 = 2*2, 9 = 3*3, 25 = 5*5 and 36 = 6*6. I don’t know why square bases don’t have max-period prime reciprocals, but it’s probably obvious to anyone with more mathematical nous than me.

Period pane for primes 3..2939 and bases 2..302

Period pane for primes 3..6553 and bases 2..602

Like the Ulam spiral, other and more mysterious patterns appear in the period panes, hinting at the hidden regularities in the primes.

Sliv and Let Tri

Tuesday, 13th Apr, 2021 by Krilling for Company in Integer Sequences, Mathematics and tagged Arithmetic, elephant, Gregory the Great, lamb, Latin quotations, math, mathematics, maths, partitions, partitions of n, Pope Gregory I, prime numbers, primes, products, recreational math, recreational mathematics, recreational maths, river, St Gregory, sums | Leave a comment

“Fluvius, planus et altus, in quo et agnus ambulet et elephas natet,” wrote Pope Gregory the Great (540-604). “There’s a river, wide and deep, where a lamb may wade and an elephant swim.” He was talking about the Word of God, but you can easily apply his words to mathematics. However, in the river of mathematics, the very shallow and the very deep are often a single step apart.

Here’s a good example. Take the integer 2. How many different ways can it be represented as an sum of separate integers? Easy. First of all it can be represented as itself: 2 = 2. Next, it can be represented as 2 = 1 + 1. And that’s it. There are two partitions of 2, as mathematicians say:

2 = 2 = 1+1 (p=2)

Now try 3, 4, 5, 6:

3 = 3 = 1+2 = 1+1+1 (p=3) 4 = 4 = 1+3 = 2+2 = 1+1+2 = 1+1+1+1 (p=5) 5 = 5 = 1+4 = 2+3 = 1+1+3 = 1+2+2 = 1+1+1+2 = 1+1+1+1+1 (p=7) 6 = 6 = 1+5 = 2+4 = 3+3 = 1+1+4 = 1+2+3 = 2+2+2 = 1+1+1+3 = 1+1+2+2 = 1+1+1+1+2 = 1+1+1+1+1+1 (p=11)

So the partitions of 2, 3, 4, 5, 6 are 2, 3, 5, 7, 11. That’s interesting — the partition-counts are the prime numbers in sequence. So you might conjecture that p(7) = 13 and p(8) = 17. Alas, you’d be wrong. Here are the partitions of n = 1..10:

1 = 1 (p=1) 2 = 2 = 1+1 (p=2) 3 = 3 = 1+2 = 1+1+1 (p=3) 4 = 4 = 1+3 = 2+2 = 1+1+2 = 1+1+1+1 (p=5) 5 = 5 = 1+4 = 2+3 = 1+1+3 = 1+2+2 = 1+1+1+2 = 1+1+1+1+1 (p=7) 6 = 6 = 1+5 = 2+4 = 3+3 = 1+1+4 = 1+2+3 = 2+2+2 = 1+1+1+3 = 1+1+2+2 = 1+1+1+1+2 = 1+1+1+1+1+1 (p=11) 7 = 7 = 1+6 = 2+5 = 3+4 = 1+1+5 = 1+2+4 = 1+3+3 = 2+2+3 = 1+1+1+4 = 1+1+2+3 = 1+2+2+2 = 1+1+1+1+3 = 1+1+1+2+2 = 1+1+1+1+1+2 = 1+1+1+1+1+1+1 (p=15) 8 = 8 = 1+7 = 2+6 = 3+5 = 4+4 = 1+1+6 = 1+2+5 = 1+3+4 = 2+2+4 = 2+3+3 = 1+1+1+5 = 1+1+2+4 = 1+1+3+3 = 1+2+2+3 = 2+2+2+2 = 1+1+1+1+4 = 1+1+1+2+3 = 1+1+2+2+2 = 1+1+1+1+1+3 = 1+1+1+1+2+2 = 1+1+1+1+1+1+2 = 1+1+1+1+1+1+1+1 (p=22) 9 = 9 = 1+8 = 2+7 = 3+6 = 4+5 = 1+1+7 = 1+2+6 = 1+3+5 = 1+4+4 = 2+2+5 = 2+3+4 = 3+3+3 = 1+1+1+6 = 1+1+2+5 = 1+1+3+4 = 1+2+2+4 = 1+2+3+3 = 2+2+2+3 = 1+1+1+1+5 = 1+1+1+2+4 = 1+1+1+3+3 = 1+1+2+2+3 = 1+2+2+2+2 = 1+1+1+1+1+4 = 1+1+1+1+2+3 = 1+1+1+2+2+2 = 1+1+1+1+1+1+3 = 1+1+1+1+1+2+2 = 1+1+1+1+1+1+1+2 = 1+1+1+1+1+1+1+1+1 (p=30) 10 = 10 = 1+9 = 2+8 = 3+7 = 4+6 = 5+5 = 1+1+8 = 1+2+7 = 1+3+6 = 1+4+5 = 2+2+6 = 2+3+5 = 2+4+4 = 3+3+4 = 1+1+1+7 = 1+1+2+6 = 1+1+3+5 = 1+1+4+4 = 1+2+2+5 = 1+2+3+4 = 1+3+3+3 = 2+2+2+4 = 2+2+3+3 = 1+1+1+1+6 = 1+1+1+2+5 = 1+1+1+3+4 = 1+1+2+2+4 = 1+1+2+3+3 = 1+2+2+2+3 = 2+2+2+2+2 = 1+1+1+1+1+5 = 1+1+1+1+2+4 = 1+1+1+1+3+3 = 1+1+1+2+2+3 = 1+1+2+2+2+2 = 1+1+1+1+1+1+4 = 1+1+1+1+1+2+3 = 1+1+1+1+2+2+2 = 1+1+1+1+1+1+1+3 = 1+1+1+1+1+1+2+2 = 1+1+1+1+1+1+1+1+2 = 1+1+1+1+1+1+1+1+1+1 (p=42)

It’s very simple to understand what a partition is, but very difficult to say how many partitions, p(n), a particular number will have. Here’s a partition: 11 = 4 + 3 + 2 + 2. But what is p(11)? Is there a formula for the sequence of p(n)?

1, 2, 3, 5, 7, 11, 15, 22, 30, 42, 56, 77, 101, 135, 176, 231, 297, 385, 490, 627, 792, 1002, 1255, 1575, 1958, 2436, 3010, 3718, 4565, 5604, 6842, 8349, 10143, 12310, 14883, 17977, 21637, 26015, 3118 5, 37338, 44583, 53174, 63261... (A000041 at the OEIS)

Yes, there is a formula, but it is very difficult to understand the Partition function that supplies it. So that part of the river of mathematics is very deep. But a step away the river of mathematics is very shallow. Here’s another question: If you multiply the numbers in a partition of n, what’s the largest possible product? Try using the partitions of 5:

4 = 1 * 4 6 = 2 * 3 3 = 1 * 1 * 3 4 = 1 * 2 * 2 2 = 1 * 1 * 1 * 2 1 = 1 * 1 * 1 * 1 * 1

The largest product is 6 = 2 * 3. So the answer is easy for n = 5, but I assumed that as n got bigger, the largest product got more interesting, using a subtler and subtler mix of prime factors. I was wrong. You don’t have to struggle to find a formula for what you might call the maximum multiplicity of the partitions of n:

1 = 1 (n=1) 2 = 2 (n=2) 3 = 3 (n=3) 4 = 2 * 2 (n=4) 6 = 2 * 3 (n=5) 9 = 3 * 3 (n=6) 12 = 2 * 2 * 3 (n=7) 18 = 2 * 3 * 3 (n=8) 27 = 3 * 3 * 3 (n=9) 36 = 2 * 2 * 3 * 3 (n=10) 54 = 2 * 3 * 3 * 3 (n=11) 81 = 3 * 3 * 3 * 3 (n=12) 108 = 2 * 2 * 3 * 3 * 3 (n=13) 162 = 2 * 3 * 3 * 3 * 3 162(n=14) 243 = 3 * 3 * 3 * 3 * 3 (n=15) 324 = 2 * 2 * 3 * 3 * 3 * 3 (n=16) 486 = 2 * 3 * 3 * 3 * 3 * 3 (n=17) 729 = 3 * 3 * 3 * 3 * 3 * 3 (n=18)

It’s easy to see why the greatest prime factor is always 3. If you use 5 or 7 as a factor, the product can always be beaten by splitting the 5 into 2*3 or the 7 into 2*2*3:

15 = 3 * 5 < 18 = 3 * 2*3 (n=8) 14 = 2 * 7 < 24 = 2 * 2*2*3 (n=9) 35 = 5 * 7 < 72 = 2*3 * 2*2*3 (n=12)

And if you’re using 7 → 2*2*3 as factors, you can convert them to 1*3*3, then add the 1 to another factor to make a bigger product still:

14 = 2 * 7 < 24 = 2 * 2*2*3 < 27 = 3 * 3 * 3 (n=9) 35 = 5 * 7 < 72 = 2*3 * 2*2*3 < 81 = 3 * 3 * 3 * 3 (n=12)

Post-Performative Post-Scriptum

The title of this post is, of course, a paronomasia on core Beatles album Live and Let Die (1954). But what does it mean? Well, if you think of the partitions of n as slivers of n, then you sliv n to find its partitions:

9 = 9 = 1+8 = 2+7 = 3+6 = 4+5 = 1+1+7 = 1+2+6 = 1+3+5 = 1+4+4 = 2+2+5 = 2+3+4 = 3+3+3 = 1+1+1+6 = 1+1+2+5 = 1+1+3+4 = 1+2+2+4 = 1+2+3+3 = 2+2+2+3 = 1+1+1+1+5 = 1+1+1+2+4 = 1+1+1+3+3 = 1+1+2+2+3 = 1+2+2+2+2 = 1+1+1+1+1+4 = 1+1+1+1+2+3 = 1+1+1+2+2+2 = 1+1+1+1+1+1+3 = 1+1+1+1+1+2+2 = 1+1+1+1+1+1+1+2 = 1+1+1+1+1+1+1+1+1 (p=30)

And when you find the greatest product among those partitions, you let 3 or “tri” work its multiplicative magic. So you “Sliv and Let Tri”:

8 = 1 * 8 14 = 2 * 7 18 = 3 * 6 20 = 4 * 5 7 = 1 * 1 * 7 12 = 1 * 2 * 6 15 = 1 * 3 * 5 16 = 1 * 4 * 4 20 = 2 * 2 * 5 24 = 2 * 3 * 4 27 = 3 * 3 * 3 ← 6 = 1 * 1 * 1 * 6 10 = 1 * 1 * 2 * 5 12 = 1 * 1 * 3 * 4 16 = 1 * 2 * 2 * 4 12 = 1 * 2 * 3 * 3 24 = 2 * 2 * 2 * 3 5 = 1 * 1 * 1 * 1 * 5 8 = 1 * 1 * 1 * 2 * 4 9 = 1 * 1 * 1 * 3 * 3 12 = 1 * 1 * 2 * 2 * 3 16 = 1 * 2 * 2 * 2 * 2 4 = 1 * 1 * 1 * 1 * 1 * 4 6 = 1 * 1 * 1 * 1 * 2 * 3 8 = 1 * 1 * 1 * 2 * 2 * 2 3 = 1 * 1 * 1 * 1 * 1 * 1 * 3 4 = 1 * 1 * 1 * 1 * 1 * 2 * 2 2 = 1 * 1 * 1 * 1 * 1 * 1 * 1 * 2 1 = 1 * 1 * 1 * 1 * 1 * 1 * 1 * 1 * 1

Year and Square

Thursday, 3rd Jan, 2019 by Krilling for Company in 666, Magic squares, Mathematics, Number of the Beast, Prime numbers and tagged 111, 2019, 3x3 magic square, 666, 673, Luoshu square, magic squares, prime magic squares, prime numbers, primes | Leave a comment

The simplest and in some ways greatest magic square is this:

6 1 8
7 5 3
2 9 4 (Magic total = 15)

All rows and columns sum to 15 and so do both diagonals. Using other sets of numbers, you can create an infinite number of further 3×3 magic squares. Here’s one using only prime numbers and 1:

43 01 67
61 37 13
07 73 31 (Magic=111)

The magic total is 111, which is 3 x 37, just as 15 = 3 x 5. It’s an interesting but untaxing exercise to prove that, for all 3×3 magic squares, the magic total is three times the central number. So you can use only prime numbers in a 3×3 square, but you can’t have a prime number as the magic total (unless you use fractions and so on).

And guess what? 2019 = 3 x 667, the first prime number after 666. So I decided to see if I could find an all-prime magic squares whose magic total was 2019. I found nine of them (and 9 = 3 x 3).

1117 0019 0883
0439 0673 0907
0463 1327 0229 (Magic=2019)

1069 0067 0883
0487 0673 0859
0463 1279 0277 (Magic=2019)

1063 0229 0727
0337 0673 1009
0619 1117 0283 (Magic=2019)

0883 0313 0823
0613 0673 0733
0523 1033 0463 (Magic=2019)

0619 0337 1063
1117 0673 0229
0283 1009 0727 (Magic=2019)

0463 0439 1117
1327 0673 0019
0229 0907 0883 (Magic=2019)

0463 0487 1069
1279 0673 0067
0277 0859 0883 (Magic=2019)

0379 0607 1033
1327 0673 0019
0313 0739 0967 (Magic=2019)

0523 0613 0883
1033 0673 0313
0463 0733 0823 (Magic=2019)

WhirlpUlam

Wednesday, 1st Aug, 2018 by Krilling for Company in Integer Sequences, Mathematics, Prime numbers, Ulam Spirals and tagged 41, David Wells, Euler, integer spiral, Penguin Dictionary of Curious and Interesting Numbers, polynomial functions, prime formula, prime formulae, prime formulas, prime numbers, prime spiral, primes, Stanislaw Ulam, Ulam diagonals, Ulam Spirals, Ulam spokes | Leave a comment

Stanislaw Ulam (pronounced OO-lam) was an American mathematician who was doodling one day in 1963 and created what is now called the Ulam spiral. It’s a spiral of integers on a square grid with the prime squares filled in and the composite squares left empty. At the beginning it looks like this (the blue square is the integer 1, with 2 to the east, 3 to the north-east, 4 to the north, 5 to the north-west, 6 to the west, and so on):

Ulam spiral

And here’s an Ulam spiral with more integers:

Ulam spiral at higher resolution

The primes aren’t scattered at random over the spiral: they often fall into lines that are related to what are called polynomial functions, such as n² + n + 1. To understand polynomial functions better, let’s look at how the Ulam spiral is made. Here is a text version with the primes underlined:

Here’s an animated version:

Here’s the true spiral again with 1 marked as a blue square:

Ulam spiral centred on 1

What happens when you try other numbers at the centre? Here’s 2 at the centre as a purple square, because it’s prime:

Ulam spiral centred on 2

And 3 at the centre, also purple because it’s also prime:

Ulam spiral centred on 3

And 4 at the centre, blue again because 4 = 2^2:

Ulam spiral centred on 4

And 5 at the centre, prime and purple:

Ulam spiral centred on 5

Each time the central number changes, the spiral shifts fractionally. Here’s an animation of the central number shifting from 1 to 41. If you watch, you’ll see patterns remaining stable, then breaking up as the numbers shift towards the center and disappear (the central number is purple if prime, blue if composite):

Ulam whirlpool, or WhirlpUlam

I think the animation looks like a whirlpool or whirlpUlam (prounced whirlpool-am), as numbers spiral towards the centre and disappear. You can see the whirlpUlam more clearly here:

An animated Ulam Spiral pausing at n=11, 17, 41

WhirlpUlam again

Note that something interesting happens when the central number is 41. The spiral is bisected by a long line of prime squares, like this:

Ulam spiral centred on 41

The line is actually a visual representation of something David Wells wrote about in The Penguin Dictionary of Curious and Interesting Numbers (1986):

Euler discovered the excellent and famous formula x² + x + 41, which gives prime values for x = 0 to 39.

Here are the primes generated by the formula:
41, 43, 47, 53, 61, 71, 83, 97, 113, 131, 151, 173, 197, 223, 251, 281, 313, 347, 383, 421, 461, 503, 547, 593, 641, 691, 743, 797, 853, 911, 971, 1033, 1097, 1163, 1231, 1301, 1373, 1447, 1523, 1601
You’ll see other lines appear and disappear as the whirlpUlam whirls:

Ulam spiral centred on 17

Primes in line: 17, 19, 23, 29, 37, 47, 59, 73, 89, 107, 127, 149, 173, 199, 227, 257 (n=0..15)

Ulam spiral centred on 59

Primes in line: 59, 67, 83, 107, 139, 179, 227, 283, 347, 419, 499, 587, 683, 787 (n=0..13)

Ulam spiral centred on 163

Primes in line: 163, 167, 179, 199, 227, 263, 307, 359, 419, 487, 563, 647, 739, 839, 947, 1063, 1187, 1319, 1459, 1607 (n=0..19)

Ulam spiral centred on 233

Primes in line: 233, 241, 257, 281, 313, 353, 401, 457, 521, 593, 673, 761, 857 ((n=0..12)

Ulam spiral centred on 653

Primes in line: 653, 661, 677, 701, 733, 773, 821, 877, 941, 1013, 1093, 1181, 1277, 1381, 1493, 1613, 1741, 1877 (n=0..17)

Ulam spiral centred on 409,333

Primes in line: 409,333, 409337, 409349, 409369, 409397, 409433, 409477, 409529, 409589, 409657, 409733, 409817, 409909, 410009, 410117, 410233 (n=0..15)

Some bisect the centre, some don’t, because you could say that the Ulam spiral has six diagonals, two that bisect the centre (top-left-to-bottom-right and bottom-left-to-top-right) and four that don’t. You could also call them spokes:

If you look at the integers in the spokes, you can see that they’re generated by polynomial functions in which c stands for the central number:
North-west spoke: 1, 5, 17, 37, 65, 101, 145, 197, 257, 325, 401, 485, 577, 677, 785, 901, 1025, 1157, 1297, 1445, 1601, 1765, 1937, 2117, 2305, 2501, 2705, 2917... = c + (2n)^2

South-east spoke: 1, 9, 25, 49, 81, 121, 169, 225, 289, 361, 441, 529, 625, 729, 841, 961, 1089, 1225, 1369, 1521, 1681, 1849, 2025, 2209, 2401, 2601, 2809, 3025, 3249, 3481, 3721, 3969, 4225, 4489, 4761, 5041, 5329, 5625... = c+(2n+1)^2-1 NW-SE diagonal: 1, 5, 9, 17, 25, 37, 49, 65, 81, 101, 121, 145, 169, 197, 225, 257, 289, 325, 361, 401, 441, 485, 529, 577, 625, 677, 729, 785, 841, 901, 961, 1025, 1089, 1157, 1225, 1297, 1369, 1445, 1521, 1601, 1681 = c + n^2 + 1 - (n mod 2) North-east spoke: 1, 3, 13, 31, 57, 91, 133, 183, 241, 307, 381, 463, 553, 651, 757, 871, 993, 1123, 1261, 1407, 1561, 1723, 1893, 2071... = c + (n+1)^2 - n - 1 South-west spoke: 1, 7, 21, 43, 73, 111, 157, 211, 273, 343, 421, 507, 601, 703, 813, 931, 1057, 1191, 1333, 1483, 1641, 1807, 1981, 2163... = c + (2n)^2 + 2n SW-NE diagonal: 1, 3, 7, 13, 21, 31, 43, 57, 73, 91, 111, 133, 157, 183, 211, 241, 273, 307, 343, 381, 421, 463, 507, 553, 601, 651, 703, 757, 813, 871, 931, 993, 1057, 1123, 1191, 1261, 1333, 1407, 1483, 1561, 1641... = c + n^2 + n

Elsewhere other-engageable:

• All posts interrogating issues around the Ulam spiral

Square on a Three String

Tuesday, 3rd Oct, 2017 by Krilling for Company in Base Behavior, φ, Magic squares, Mathematics and tagged 222, 223, base 3, bases, decimals, digits, Elagabulus, golden section, Heliogabalus, integers, math, mathematics, maths, numbers, phi, prime numbers, primes, reciprocals, recreational math, recreational mathematics, recreational maths, Sir Lawrence Alma-Tadema, symmetrical pattern, Symmetry, ternary, The Roses of Heliogabalus, Victorian painting | Leave a comment

222 A.D. was the year in which the Emperor Heliogabalus was assassinated by his own soldiers. Exactly 1666 years later, the Anglo-Dutch classicist Sir Lawrence Alma-Tadema exhibited his painting The Roses of Heliogabalus (1888). I suggested in “Roses Are Golden” that Alma-Tadema must have chosen the year as deliberately as he chose the dimensions of his canvas, which, at 52″ x 84 ¹/₈“, is an excellent approximation to the golden ratio.

But did Alma-Tadema know that lines at 0º and 222º divide a circle in the golden ratio? He could easily have done, just as he could easily have known that 222 precedes the 48th prime, 223. But it is highly unlikely that he knew that 223 yields a magic square whose columns, rows and diagonals all sum to 222. To create the square, simply list the 222 multiples of the reciprocal 1/223 in base 3, or ternary. The digits of the reciprocal repeat after exactly 222 digits and its multiples begin and end like this:
001/223 = 0.00001002102101021212111012022211122022... in base 3 002/223 = 0.00002011211202120201222101122200021121... 003/223 = 0.00010021021010212121110120222111220221... 004/223 = 0.00011100200112011110221210022100120020... 005/223 = 0.00012110002220110100102222122012012120...

[...]

218/223 = 0.22210112220002112122120000100210210102... in base 3 219/223 = 0.22211122022110211112001012200122102202... 220/223 = 0.22212201201212010101112102000111002001... 221/223 = 0.22220211011020102021000121100022201101... 222/223 = 0.22221220120121201010111210200011100200...
Each column, row and diagonal of ternary digits sums to 222. Here is the full n/223 square represented with 0s in grey, 1s in white and 2s in red:

(Click for larger)

It isn’t difficult to see that the white squares are mirror-symmetrical on a horizontal axis. Here is the symmetrical pattern rotated by 90º:

(Click for larger)

But why should the 1s be symmetrical? This isn’t something special to 1/223, because it happens with prime reciprocals like 1/7 too:
1/7 = 0.010212... in base 3 2/7 = 0.021201... 3/7 = 0.102120... 4/7 = 0.120102... 5/7 = 0.201021... 6/7 = 0.212010...
And you can notice something else: 0s mirror 2s and 2s mirror 0s. A related pattern appears in base 10:
1/7 = 0.142857... 2/7 = 0.285714... 3/7 = 0.428571... 4/7 = 0.571428... 5/7 = 0.714285... 6/7 = 0.857142...
The digit 1 in the decimal digits of n/7 corresponds to the digit 8 in the decimal digits of (7-n)/7; 4 corresponds to 5; 2 corresponds to 7; 8 corresponds to 1; 5 corresponds to 4; and 7 corresponds to 2. In short, if you’re given the digits d1 of n/7, you know the digits d2 of (n-7)/7 by the rule d2 = 9-d1.

Why does that happen? Examine these sums:
1/7 = 0.142857142857142857142857142857142857142857... +6/7 = 0.857142857142857142857142857142857142857142... 7/7 = 0.999999999999999999999999999999999999999999... = 1.0

2/7 = 0.285714285714285714285714285714285714285714... +5/7 = 0.714285714285714285714285714285714285714285... 7/7 = 0.999999999999999999999999999999999999999999... = 1.0

3/7 = 0.428571428571428571428571428571428571428571... +4/7 = 0.571428571428571428571428571428571428571428... 7/7 = 0.999999999999999999999999999999999999999999... = 1.0
And here are the same sums in ternary (where the first seven integers are 1, 2, 10, 11, 12, 20, 21):
1/21 = 0.010212010212010212010212010212010212010212... +20/21 = 0.212010212010212010212010212010212010212010... 21/21 = 0.222222222222222222222222222222222222222222... = 1.0

2/21 = 0.021201021201021201021201021201021201021201... +12/21 = 0.201021201021201021201021201021201021201021... 21/21 = 0.222222222222222222222222222222222222222222... = 1.0

10/21 = 0.102120102120102120102120102120102120102120... +11/21 = 0.120102120102120102120102120102120102120102... 21/21 = 0.222222222222222222222222222222222222222222... = 1.0
Accordingly, in base b with the prime p, the digits d1 of n/p correspond to the digits (p-n)/p by the rule d2 = (b-1)-d1. This explains why the 1s mirror themselves in ternary: 1 = 2-1 = (3-1)-1. In base 5, the 2s mirror themselves by the rule 2 = 4-2 = (5-1) – 2. In all odd bases, some digit will mirror itself; in all even bases, no digit will. The mirror-digit will be equal to (b-1)/2, which is always an integer when b is odd, but never an integer when b is even.

Here are some more examples of the symmetrical patterns found in odd bases:

Patterns of 1s in 1/19 in base 3

Patterns of 6s in 1/19 in base 13

Patterns of 7s in 1/19 in base 15

Elsewhere other-posted:

• Roses Are Golden — more on The Roses of Heliogabalus (1888)
• Three Is The Key — more on the 1/223 square

Get Your Ox Off

Saturday, 2nd Jul, 2016 by Krilling for Company in Clark Ashton Smith, Integer Sequences, Mathematics, Prime numbers, Reciprocals and tagged "The Demon of the Flower", Ancient Greek, animated gif, animated gifs, as the ox ploughs, boustrophedon, Clark Ashton Smith, grid, integers, math, mathematics, maths, modulus, number patterns, number-grid, numbers, oxen, prime numbers, primes, reciprocals, recreational math, recreational mathematics, recreational maths, writing | Leave a comment

Boustrophedon (pronounced “bough-stra-FEE-dun” or “boo-stra-FEE-dun”) is an ancient Greek word literally meaning “as the ox turns (in ploughing)”, that is, moving left-right, right-left, and so on. The word is used of writing that runs down the page in the same way. To see what that means, examine two versions of the first paragraph of Clark Ashton Smith’s story “The Demon of the Flower” (1933). The first is written in the usual way, the second is written boustrophedon:

Not as the plants and flowers of Earth, growing peacefully beneath a simple sun, were the blossoms of the planet Lophai. Coiling and uncoiling in double dawns; tossing tumultuously under vast suns of jade green and balas-ruby orange; swaying and weltering in rich twilights, in aurora-curtained nights, they resembled fields of rooted servants that dance eternally to an other-worldly music.

Not as the plants and flowers of Earth, growing peacefully
.iahpoL tenalp eht fo smossolb eht erew ,nus elpmis a htaeneb
Coiling and uncoiling in double dawns; tossing tumultuously
;egnaro ybur-salab dna neerg edaj fo snus tsav rednu
swaying and weltering in rich twilights, in aurora-curtained
ecnad taht stnavres detoor fo sdleif delbmeser yeht ,sthgin
eternally to an other-worldly music.

Boustrophedon writing was once common and sometimes the left-right lines would also be mirror-reversed, like this:

You could also use the term “boustrophedon” to describe the way this table of numbers is filled:

The table begins with “1” in the top left-hand corner, then moves right for “2”, then down for “3”, then right-and-up for “4”, “5” and “6”, then right for “7”, then left-and-down for “8”, “9” and “10”, and so on. You could also say that the numbers snake through the table. I’ve marked the primes among them, because I was interested in the patterns made by the primes when the numbers were represented as blocks on a grid, like this:

Primes are in solid white (compare the Ulam spiral). Here’s the boustrophedon prime-grid on a finer scale:

(click for full image)

And what about other number-tests? Here are the even numbers marked on the grid (i.e. n mod 2 = 0):

n mod 2 = 0

And here are some more examples of a modulus test:

n mod 3 = 0

n mod 5 = 0

n mod 9 = 0

n mod 15 = 0

n mod various = 0 (animated gif)

Next I looked at reciprocals (numbers divided into 1) marked on the grid, with the digits of a reciprocal marking the number of blank squares before a square is filled in (if the digit is “0”, the square is filled immediately). For example, in base ten 1/7 = 0.142857142857142857…, where the block “142857” repeats for ever. When represented on the grid, 1/7 has 1 blank square, then a filled square, then 4 blank squares, then a filled square, then 2 blank squares, then a filled square, and so on:

1/7 in base 10

And here are some more reciprocals (click for full images):

1/9 in base 2

1/13 in base 10

1/27 in base 10

1/41 in base 10

1/63 in base 10

1/82 in base 10

1/101 in base 10

1/104 in base 10

1/124 in base 10

1/143 in base 10

1/175 in base 10

1/604 in base 8

1/n in various bases (animated gif)

Overlord In Terms of Core Issues Around Maximal Engagement with Key Notions of the Über-Feral

მეფე (2) • მსოფლიოს (3) • მათემატიკა (5) •

Tag Archives: prime numbers

The Sumber of the B’s

Abounding in Abundants

Period Panes

Prime Times

Period Panes

Sliv and Let Tri

Year and Square

WhirlpUlam

Square on a Three String

Get Your Ox Off