I didn’t expect to find the hourglass fractal playing with squares. I even less expected it playing with triangles. Isosceles right triangles, to be precise. Then again, I found it first playing with the L-triomino, which is composed of three squares. And an isosceles triangle is half of a square. So it all fits. This is an isosceles right triangle:

Isosceles right triangle

It’s mirror-symmetrical, so it looks the same in a mirror unless you label one of the acute-angled corners in some way, like this:

Right triangle with labelled corner

Right triangle reflected

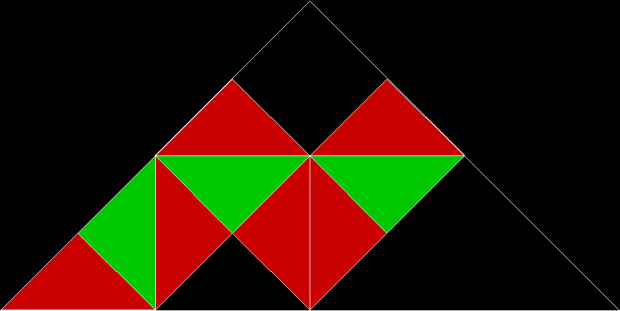
Reflection is how you find the hourglass fractal. First, divide a right triangle into four smaller right triangles.

Right triangle rep-tiled

Then discard one of the smaller triangles and repeat. If the acute corners of the smaller triangles have different orientations, one of the permutations creates the hourglass fractal, like this:

Hourglass #1

Hourglass #2

Hourglass #3

Hourglass #4

Hourglass #5

Hourglass #6

Hourglass #7

Hourglass #8

Hourglass #9

Hourglass animated

Another permutation of corners creates what I’ve decided to call the crane fractal, like this:

Crane fractal animated

Crane fractal (static)

The crane fractal is something else that I first found playing with the L-triomino:

Crane fractal from L-triomino

Previously pre-posted:

• Square Routes
• Tri Again