Category Archives: Hexagons

Points Pared

by in Geometry, Hexagons, Mathematics, Squares, Triangles and tagged , , , , , , | Leave a comment

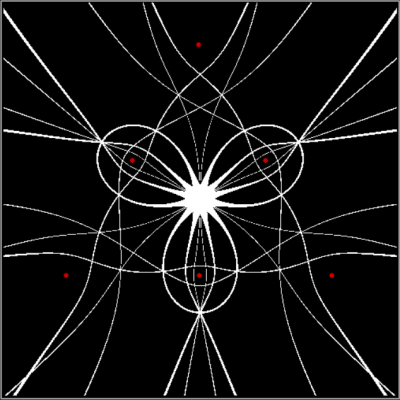
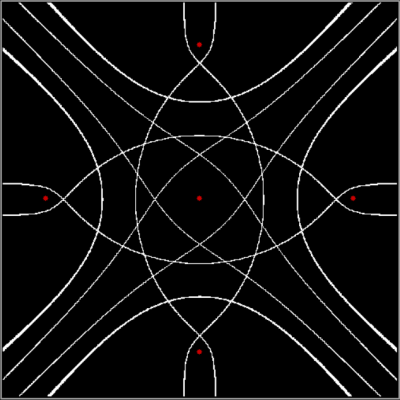
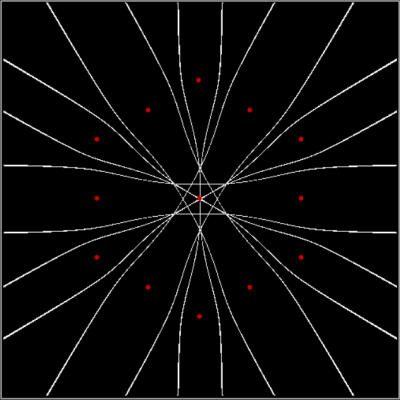
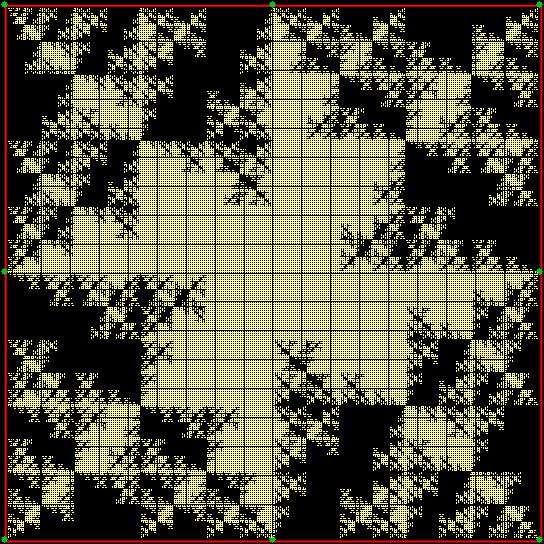
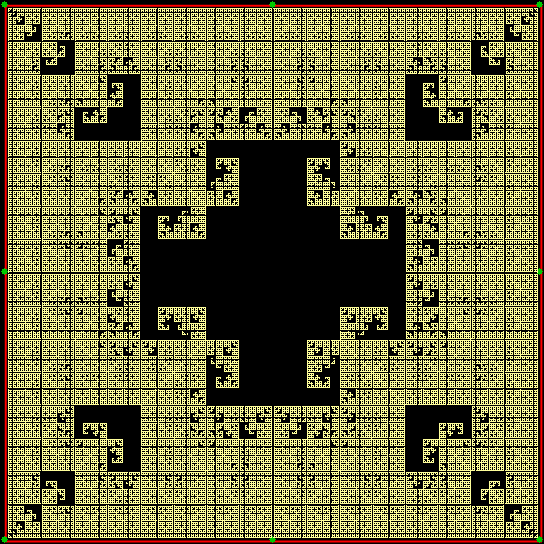There are an infinite number of points in the plane. And in part of the plane. So you have to pare points to create interesting shapes. And one way of paring them is by comparing them. The six red dots in the image below mark the three vertices of an equilateral triangle and the three mid-points of the sides. Now, test the other points in the surrounding plane and mark them in white if the average distance to (the centers of) any two of the red dots is equal to the average distance to (the centers of) the four other red dots:

Triangle + 1 side-point, sum(d1,d2)/2 = sum(d3,d4,d5,d6)/4

(click for larger)

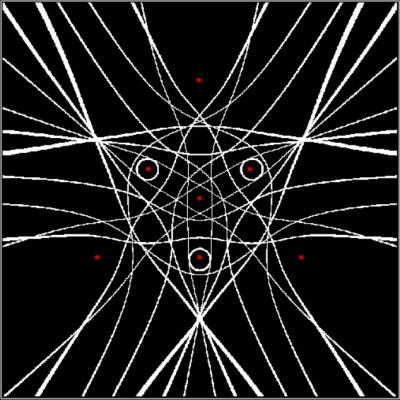
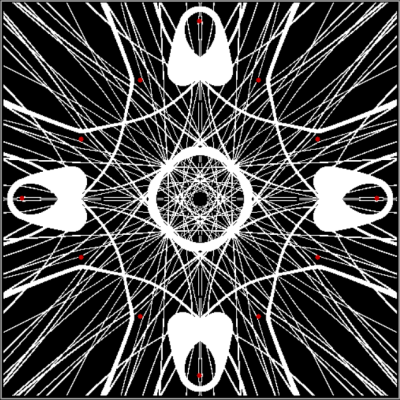
Add a central red dot to the triangle and you get this pattern:

Triangle + 1 side-point + center, distfunc(2) = distfunc(5)

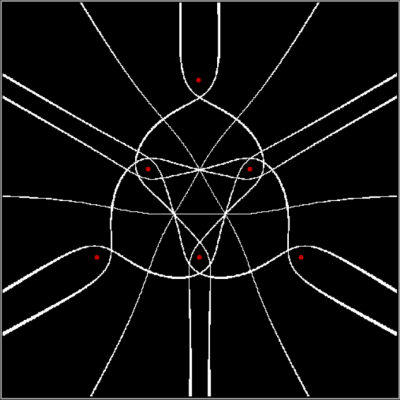
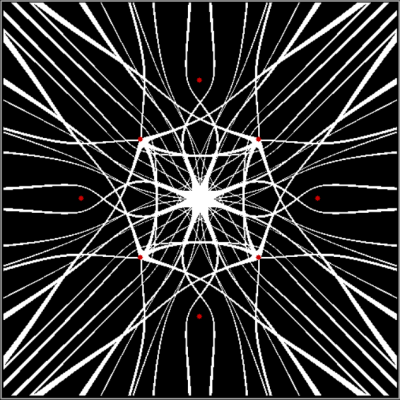
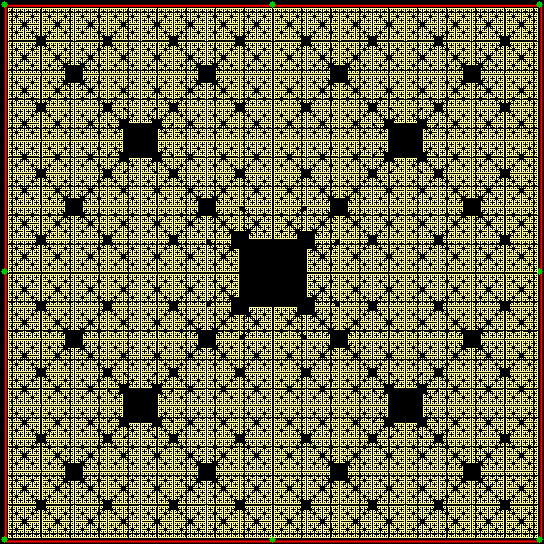
And so on:

v = 3 + sd = 2, distfunc(2) = distfunc(7)

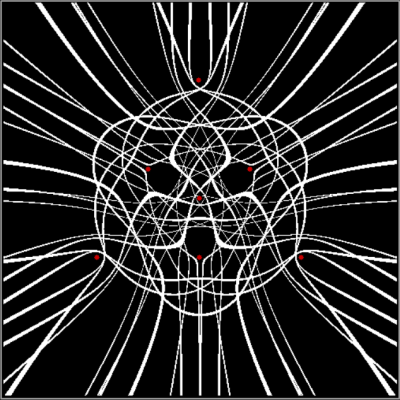
v = 3 + sd = 2 + center, distfunc(2) = distfunc(7)

v = 3 + sd = 1, distfunc(3) = distfunc(3)

v = 3 + sd = 1 + center, distfunc(3) = distfunc(7)

v = 4 + center, distfunc(2) = distfunc(3)

v = 4 + sd = 1, distfunc(2) = distfunc(6)

v = 4 + sd = 1 + center, distfunc(2) = distfunc(7)

v = 4 + sd = 2, distfunc(2) = distfunc(10)

v = 4 + sd = 2, distfunc(2) = distfunc(10) (enlarged)

v = 4 + sd = 1, distfunc(3) = distfunc(5)

v = 4 + sd = 1, distfunc(4) = distfunc(4)

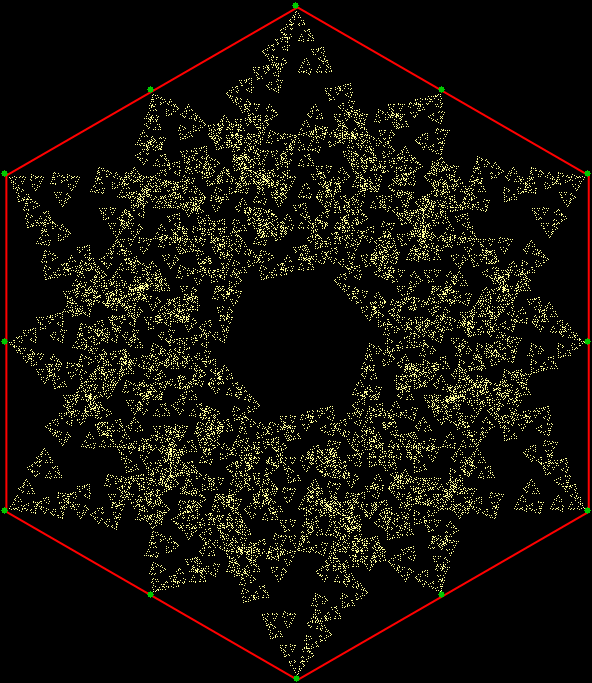
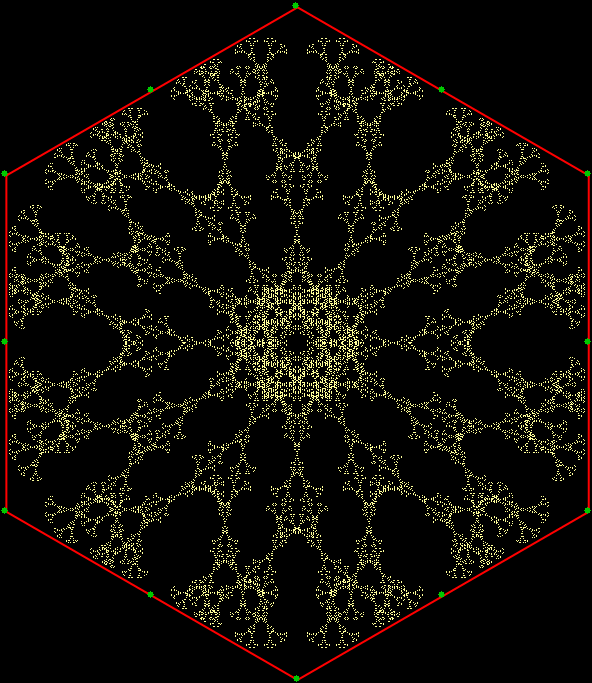
v = 5 + sd = 1, distfunc(2) = distfunc(8)

v = 5 + sd = 1, distfunc(2) = distfunc(8) (smaller scale)

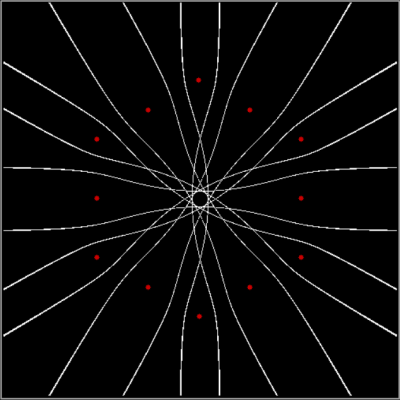
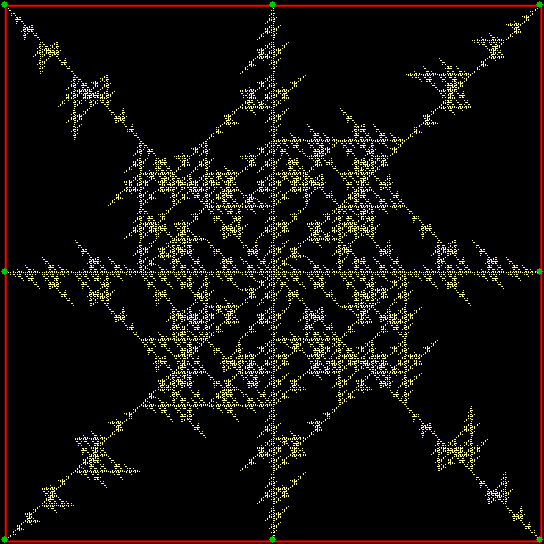
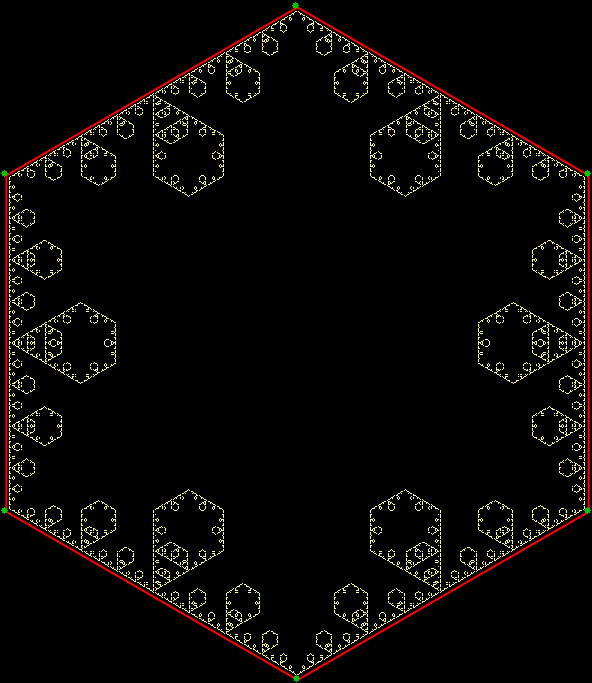
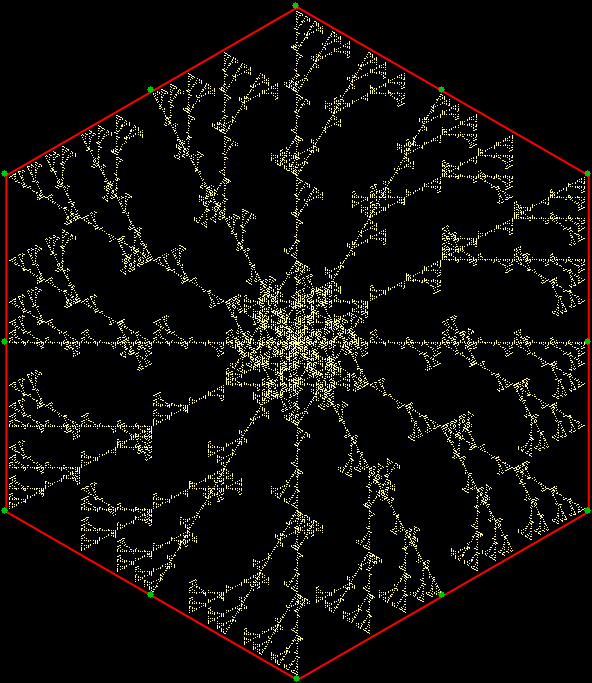
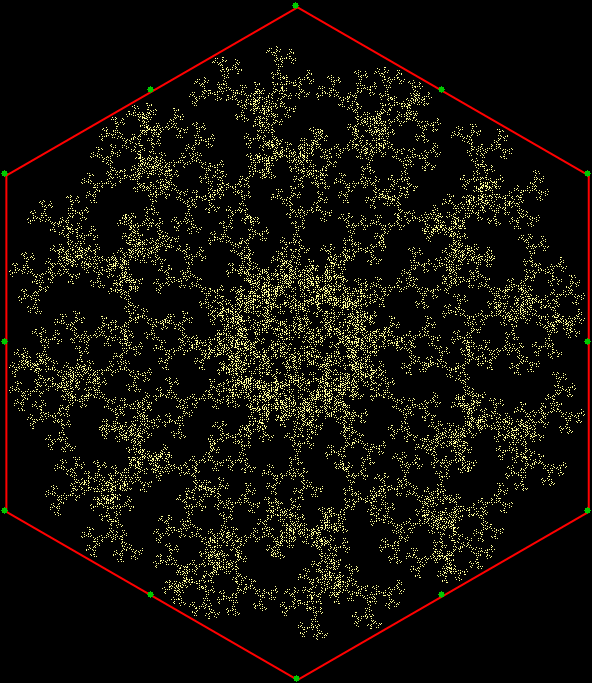
v = 6 + sd = 1, distfunc(1) = distfunc(11)

v = 6 + sd = 1 + center, distfunc(1) = distfunc(12)

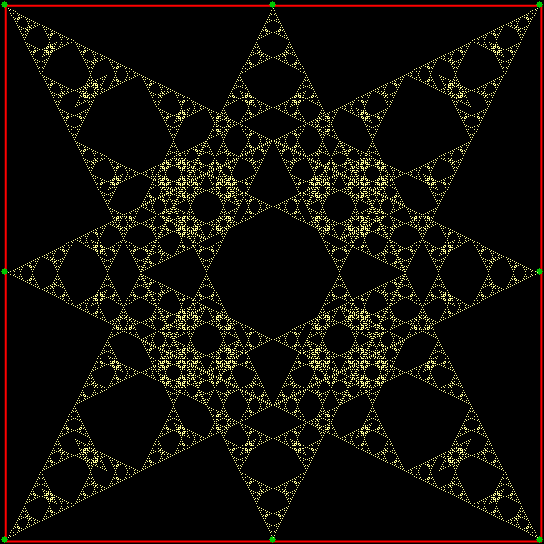
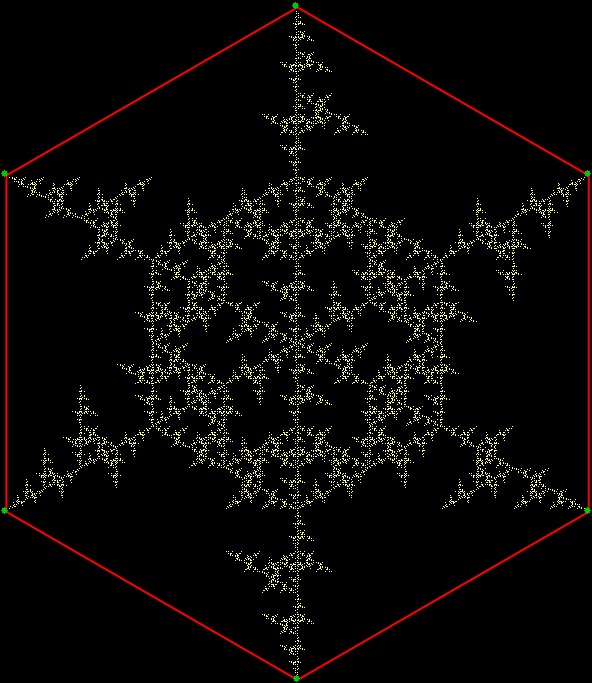
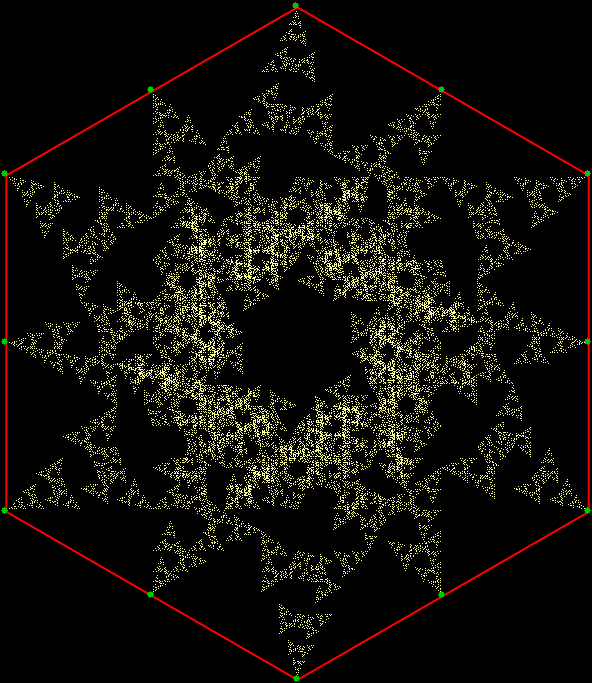
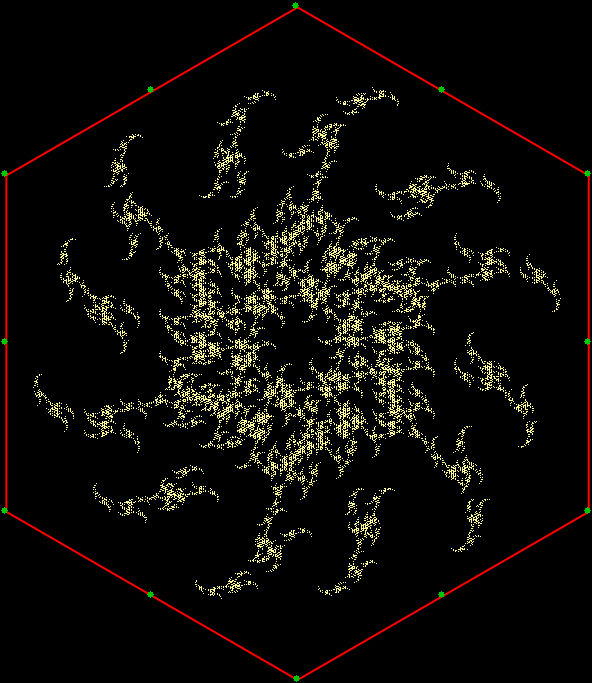
v = 6, distfunc(2) = distfunc(4)

v = 6 + center, distfunc(2) = distfunc(5)

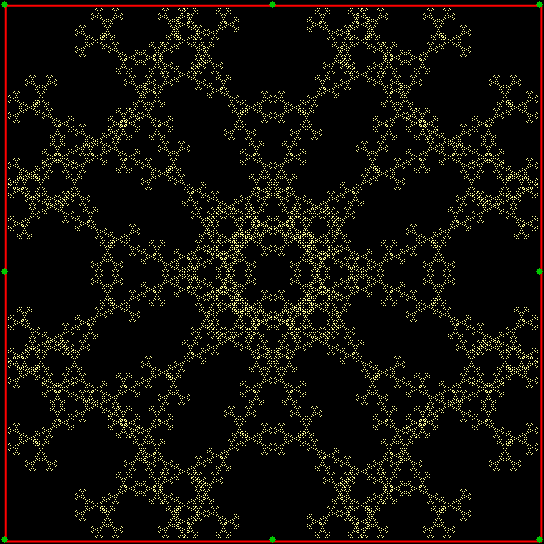
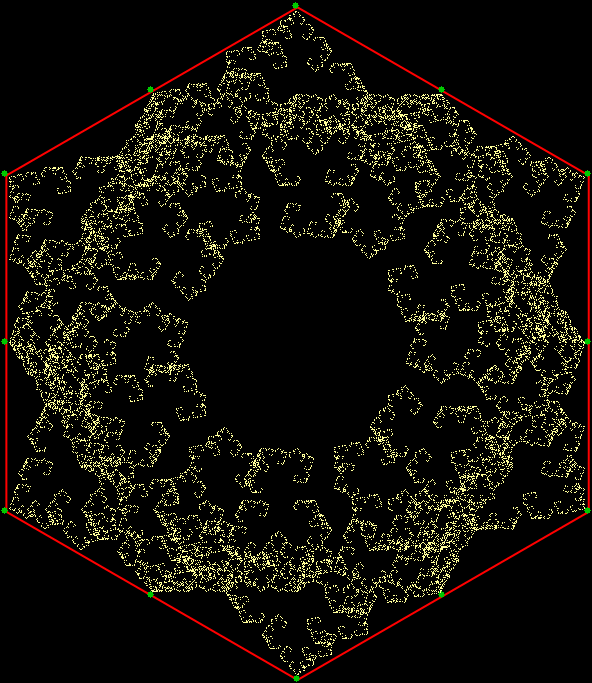
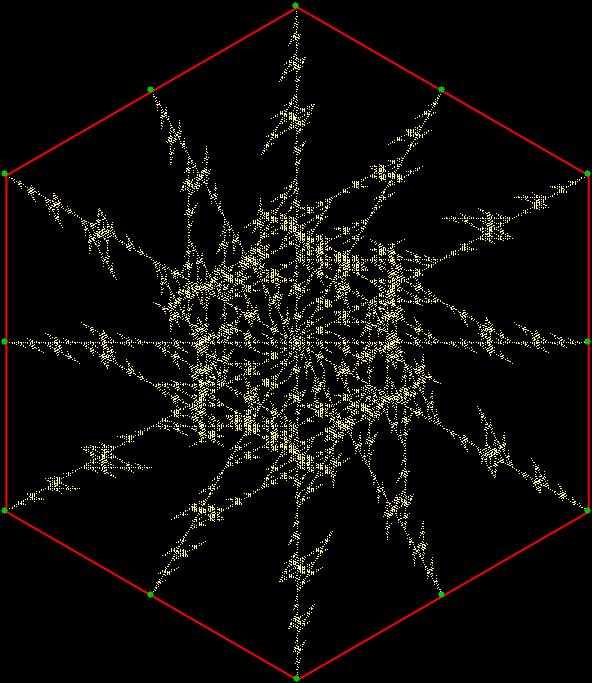
v = 6, distfunc(3) = distfunc(3)

v = 6 + center, distfunc(3) = distfunc(4)

Bent Pent

by in Geometry, Hexagons, Mathematics, Pentagons, Polygons, Puzzles, Squares and tagged , , , , , , , , , , , , , , | Leave a comment

This is a beautiful and interesting shape, reminiscent of a piece of jewellery:

Pentagons in a ring

I came across it in this tricky little word-puzzle:

Word puzzle using pentagon-ring

Here’s a printable version of the puzzle:

Printable puzzle

Let’s try placing some other regular polygons with s sides around regular polygons with s*2 sides:

Hexagonal ring of triangles

Octagonal ring of squares

Decagonal ring of pentagons

Dodecagonal ring of hexagons

Only regular pentagons fit perfectly, edge-to-edge, around a regular decagon. But all these polygonal-rings can be used to create interesting and beautiful fractals, as I hope to show in a future post.

Think Inc

by in Chaos Game, Fractals, Geometry, Hexagons, Mathematics, Pentagons, Squares and tagged , , , , , , , , , , , , , , , | Leave a comment

This is a T-square fractal:

T-square fractal

Or you could say it’s a T-square fractal with the scaffolding taken away, because there’s nothing to show how it was made. And how is a T-square fractal made? There are many ways. One of the simplest is to set a point jumping 1/2 of the way towards one or another of the four vertices of a square. If the point is banned from jumping towards the vertex two places clockwise (or counter-clockwise) of the vertex, v[i=1..4], it’s just jumped towards, you get a T-square fractal by recording each spot where the point lands.

You also get a T-square if the point is banned from jumping towards the vertex most distant from the vertex, v[i], it’s just jumped towards. The most distant vertex will always be the diagonally opposite vertex, or the vertex, v[i+2], two places clockwise of v[i]. So those two bans are functionally equivalent.

But what if you don’t talk about bans at all? You can also create a T-square fractal by giving the point three choices of increment, [0,1,3], after it jumps towards v[i]. That is, it can jump towards v[i+0], v[i+1] or v[i+3] (where 3+2 = 5 → 5-4 = 1; 3+3 = 6 → 2; 4+1 = 5 → 1; 4+2 = 6 → 2; 4+3 = 7 → 3). Vertex v[i+0] is the same vertex, v[i+1] is the vertex one place clockwise of v[i], and v[i+3] is the vertex two places clockwise of v[i].

So this method is functionally equivalent to the other two bans. But it’s easier to calculate, because you can take the current vertex, v[i], and immediately calculate-and-use the next vertex, without having to check whether the next vertex is forbidden. In other words, if you want speed, you just have to Think Inc!

Speed becomes important when you add a new jumping-target to each side of the square. Now the point has 8 possible targets to jump towards. If you impose several bans on the next jump, e.g the point can’t jump towards v[i+2], v[i+3], v[i+5], v[i+6] and v[i+7], you will have to check for five forbidden targets. But using the increment-set [0,1,4] you don’t have to check for anything. You just inc-and-go:

inc = 0, 1, 4

Here are more fractals created with the speedy inc-and-go method:

inc = 0, 2, 3

inc = 0, 2, 5

inc = 0, 3, 4

inc = 0, 3, 5

inc = 1, 4, 7

inc = 2, 4, 7

inc = 0, 1, 4, 7

inc = 0, 3, 4, 5

inc = 0, 3, 4, 7

inc = 0, 4, 5, 7

inc = 1, 2, 6, 7

With more incs, there are more possible paths for the jumping point and the fractals become more “solid”:

inc = 0, 1, 2, 4, 5

inc = 0, 1, 2, 6, 7

inc = 0, 1, 3, 5, 7

Now try applying inc-and-go to a pentagon:

inc = 0, 1, 2

(open in new window if blurred)

inc = 0, 2, 3

And add a jumping-target to each side of the pentagon:

inc = 0, 2, 5

inc = 0, 3, 6

inc = 0, 3, 7

inc = 1, 5, 9

inc = 2, 5, 8

inc = 5, 6, 9

And add two jumping-targets to each side of the pentagon:

inc = 0, 1, 7

inc = 0, 2, 12

inc = 0, 3, 11

inc = 0, 3, 12

inc = 0, 4, 11

inc = 0, 5, 9

inc = 0, 5, 10

inc = 2, 7, 13

inc = 2, 11, 13

inc = 3, 11, 13

After the pentagon comes the hexagon:

inc = 0, 1, 2

inc = 0, 1, 5

inc = 0, 3, 4

inc = 0, 3, 5

inc = 1, 3, 5

inc = 2, 3, 4

Add a jumping-target to each side of the hexagon:

inc = 0, 2, 5

inc = 0, 2, 9

inc = 0, 6, 11

inc = 0, 3, 6

inc = 0, 3, 8

inc = 0, 3, 9

inc = 0, 4, 7

inc = 0, 4, 8

inc = 0, 5, 6

inc = 0, 5, 8

inc = 1, 5, 9

inc = 1, 6, 10

inc = 1, 6, 11

inc = 2, 6, 8

inc = 2, 6, 10

inc = 3, 5, 7

inc = 3, 6, 9

inc = 6, 7, 11