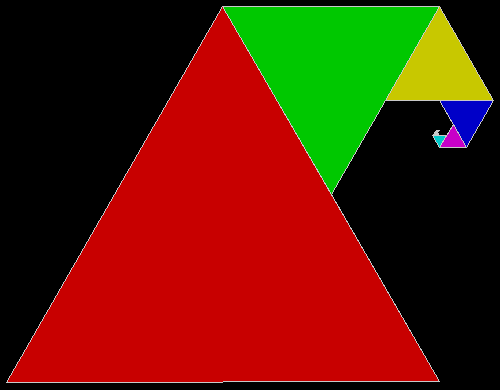
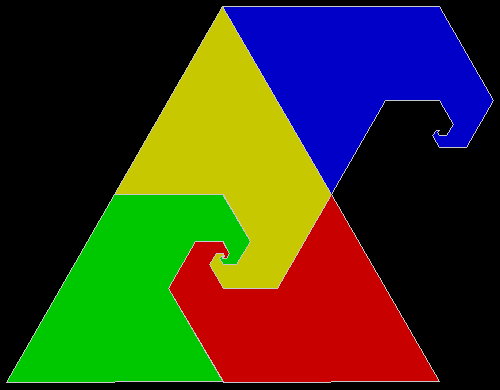
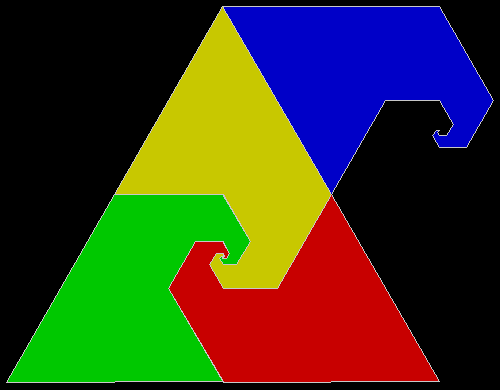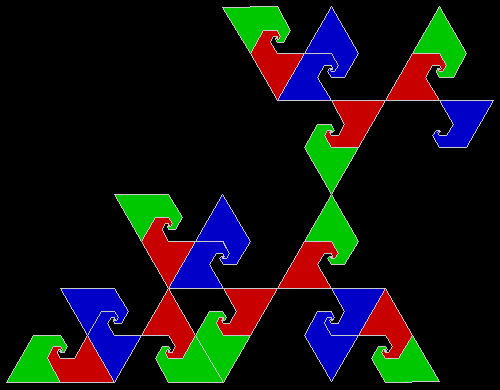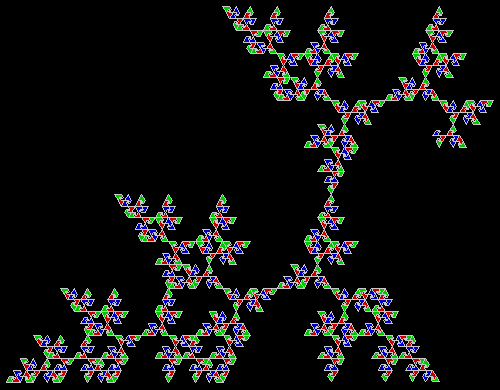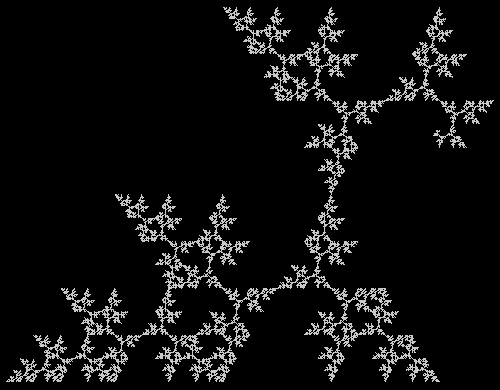
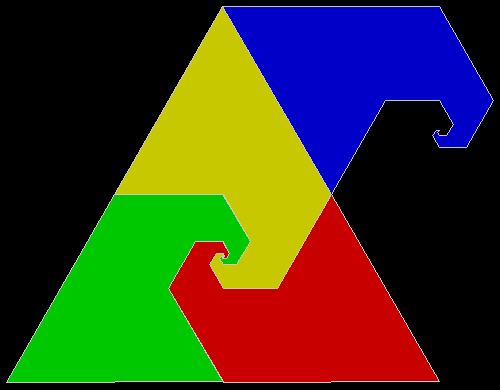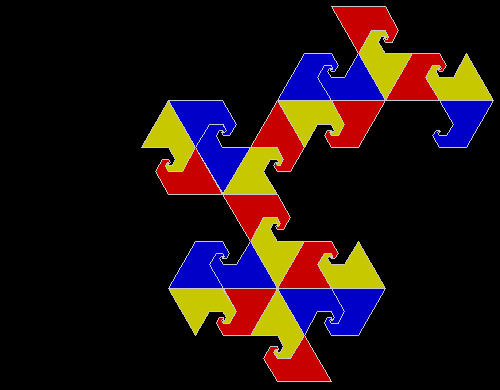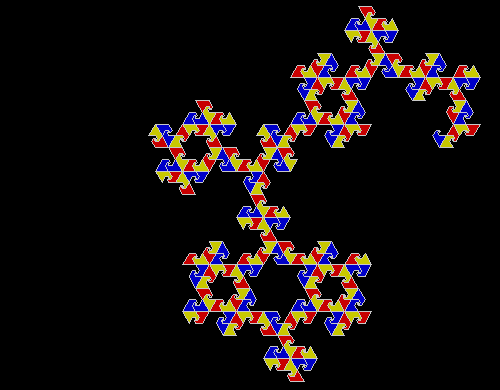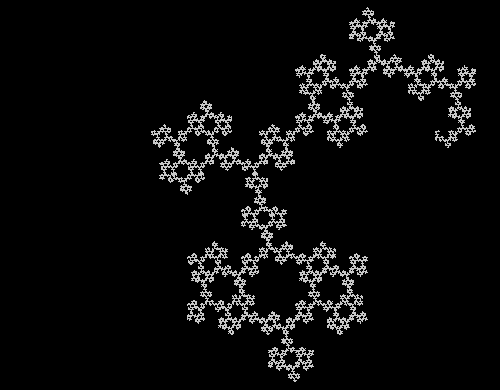
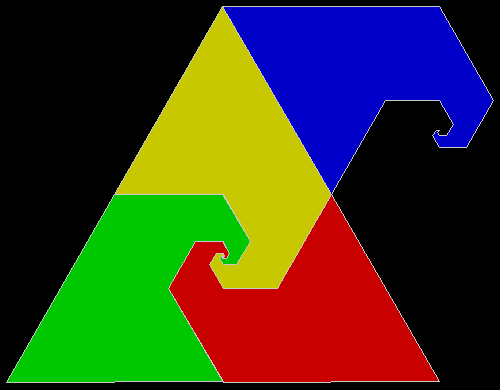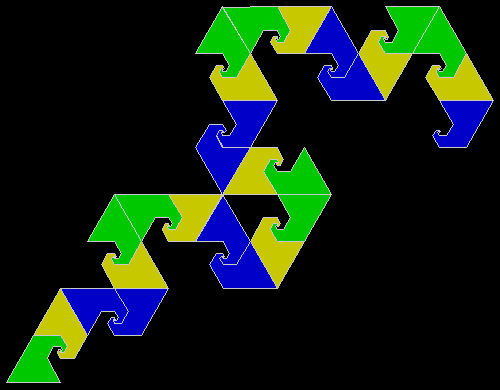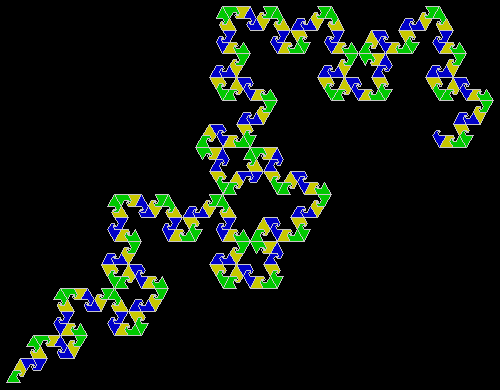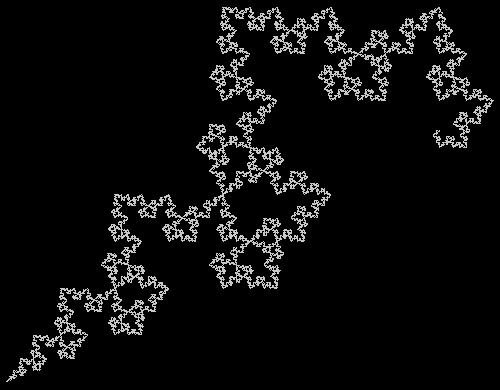
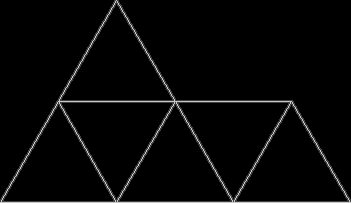
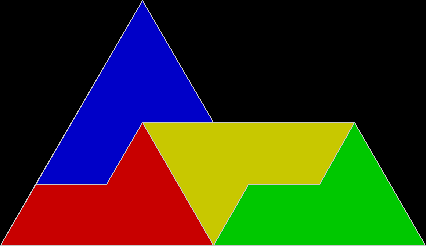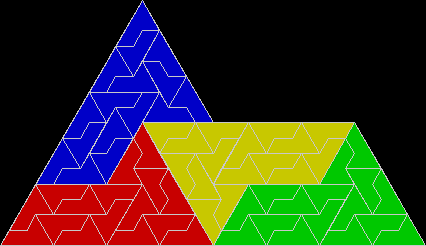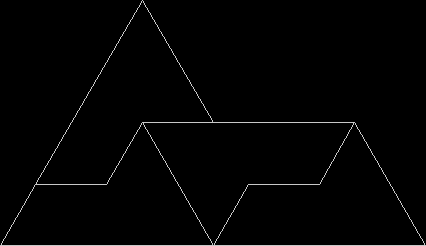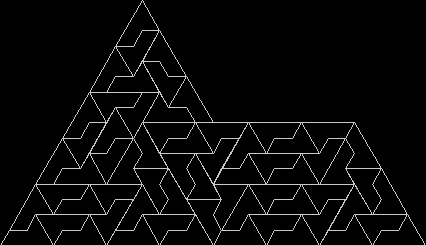
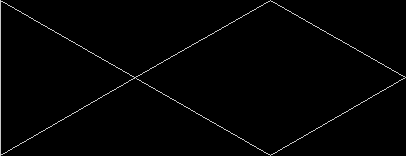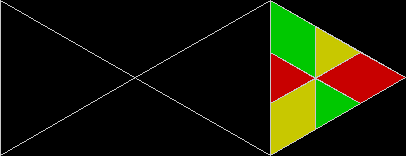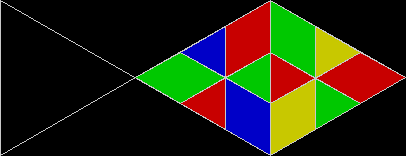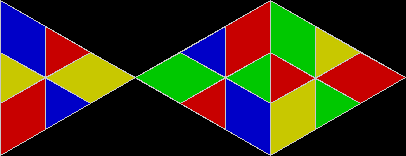
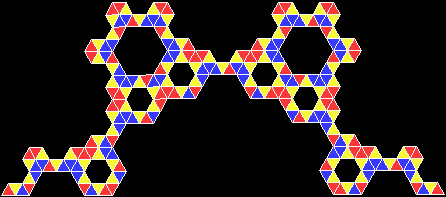
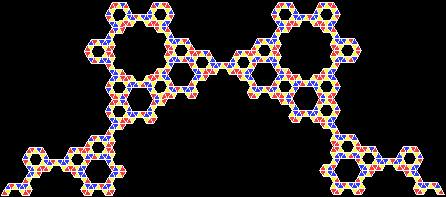
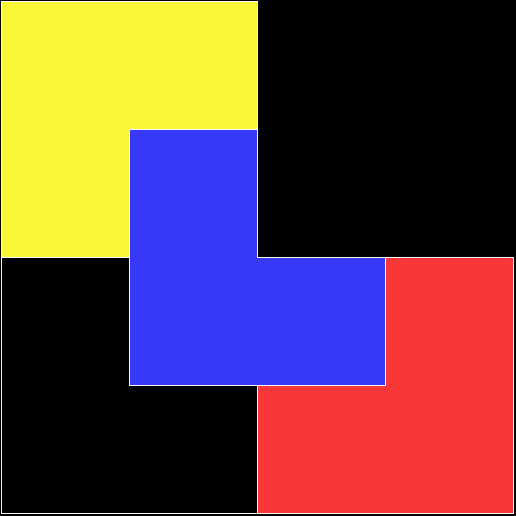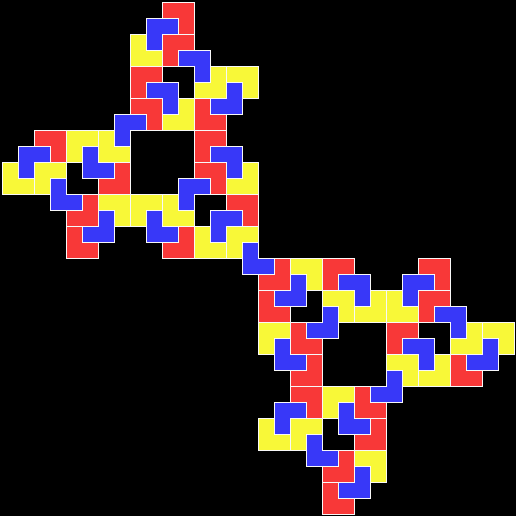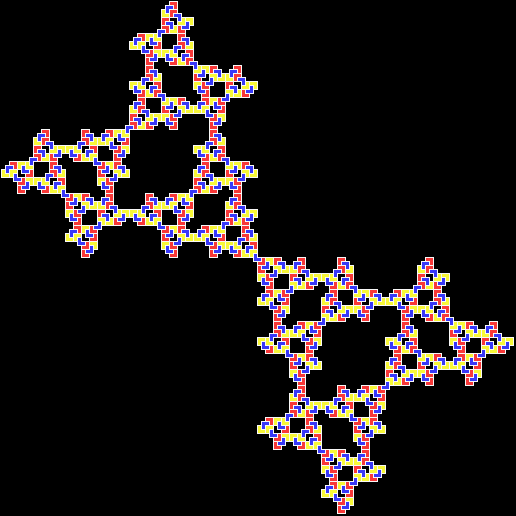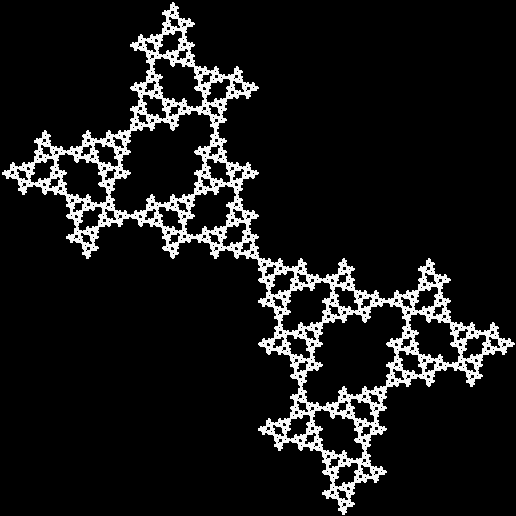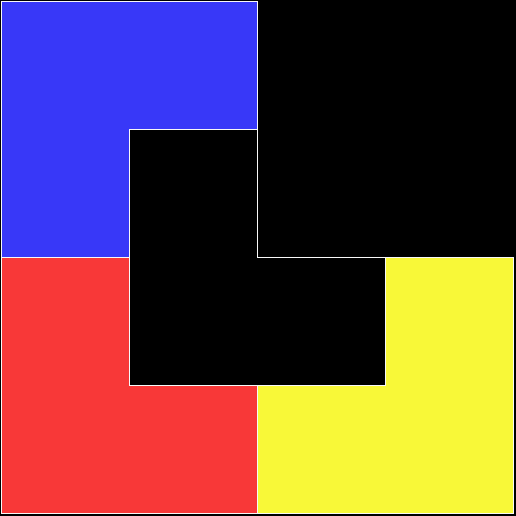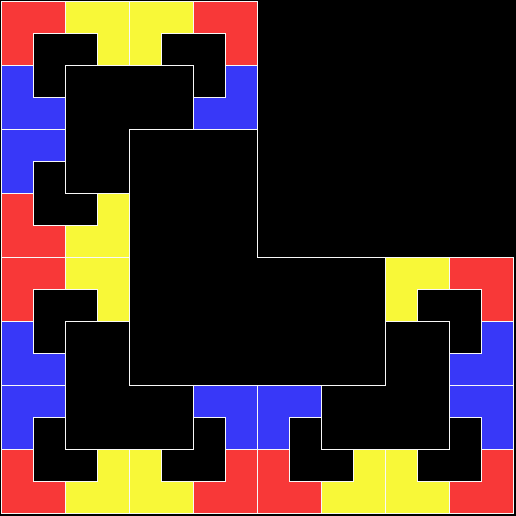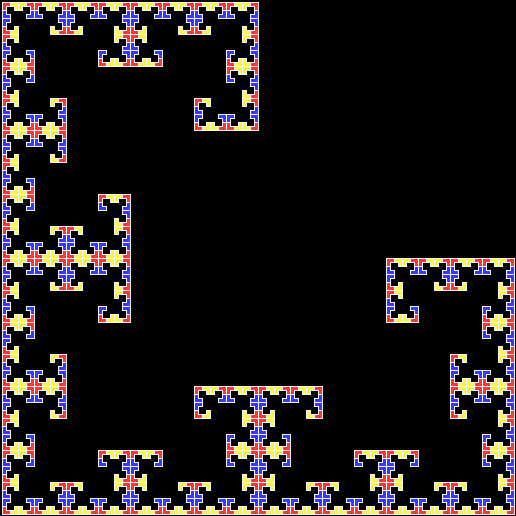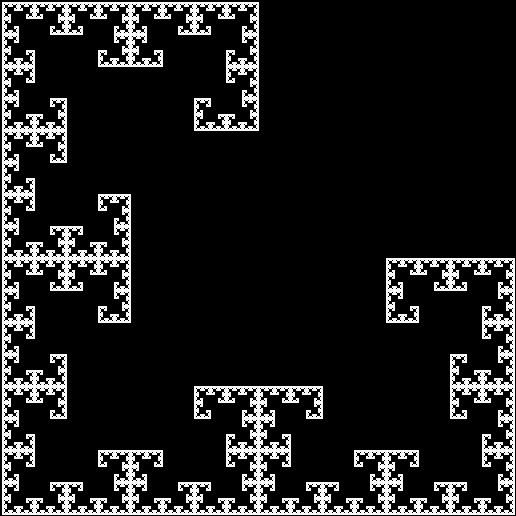Radical Sheet

Thursday, 26th May, 2016 by Krilling for Company in √2, Fractals, Mathematics, Rep-Tiles and tagged animated gif, animated gifs, √2, cross, dividing and discarding, fractal, fractal cross, fractal geometry, fractals, geometry, math, mathematics, maths, paper, paper sizes, radical, radical sheet, recreational math, recreational mathematics, recreational maths, rectangle, rectangles, sheet of paper, square root of two, tessellation, tessellations | Leave a comment

If you take a sheet of standard-sized paper and fold it in half from top to bottom, the folded sheet has the same proportions as the original, namely √2 : 1. In other words, if x = √2 / 2, then 1 / x = √2:

√2 = 1.414213562373…, √2 / 2 = 0.707106781186…, 1 / 0.707106781186… = 1.414213562373…

So you could say that paper has radical sheet (the square or other root of a number is also called its radix and √ is known as the radical sign). When a rectangle has the proportions √2 : 1, it can be tiled with an infinite number of copies of itself, the first copy having ½ the area of the original, the second ¼, the third ⅛, and so on. The radical sheet below is tiled with ten diminishing copies of itself, the final two having the same area:

You can also tile a radical sheet with six copies of itself, two copies having ¼ the area of the original and four having ⅛:

This tiling is when you might say the radical turns crucial, because you can create a fractal cross from it by repeatedly dividing and discarding. Suppose you divide a radical sheet into six copies as above, then discard two of the ⅛-sized rectangles, like this:

Stage 1

Then repeat with the smaller rectangles:

Stage 2

Stage 3

Stage 4

Stage 5

Animated version

Fractile cross

The cross is slanted, but it’s easy to rotate the original rectangle and produce an upright cross:

The Art Grows Onda

Thursday, 21st Jan, 2016 by Krilling for Company in Art, Fractals, Geometry, Mathematics, Rep-Tiles and tagged fractal, fractals, geometry, horned triangle, Ian Stewart, infinite geometry, infinite sum, Japanese art, Katsushi Hokusai, math, mathematics, maths, recreational math, recreational mathematics, recreational maths, tessellation, tessellations, The Great Wave off Kanagawa, triangle, Triangles, unicorn triangle, wave | Leave a comment

Anyone interested in recreational mathematics should seek out three compendiums by Ian Stewart: Professor Stewart’s Cabinet of Mathematical Curiosities (2008), Professor Stewart’s Hoard of Mathematical Treasures (2009) and Professor Stewart’s Casebook of Mathematical Mysteries (2014). They’re full of ideas and puzzles and are excellent introductions to the scope and subtlety of maths. I first came across Alexander’s Horned Sphere in one of them. I also came across this simpler shape that packs infinity into a finite area:

I call it a horned triangle or unicorn triangle and it reminds me of a wave curling over, like Katsushika Hokusai’s The Great Wave off Kanagawa (c. 1830) (“wave” is unda in Latin and onda in Spanish).

The Great Wave off Kanagawa by Katsushika Hokusai (1760–1849)

To construct the unicorn triangle, you take an equilateral triangle with sides of length 1 and erect a triangle with sides of length 0.5 on one of its corners. Then on the corresponding corner of the new triangle you erect a triangle with sides of length 0.25. And so on, for ever.

When you double the sides of a polygon, you quadruple the area: a 1×1 square has an area of 1, a 2×2 square has an area of 4. Accordingly, when you halve the sides of a polygon, you quarter the area: a 1×1 square has an area of 1, a 0.5 x 0.5 square has an area of 0.25 or 1/4. So if the original triangle of the unicorn triangle above has an area of 1 rather than sides of 1, the first triangle added has an area of 0.25 = 1/4, the next an area of 0.0625 = 1/16, and so on. The infinite sum is this:

1/4 + 1/16 + 1/256 + 1/1024 + 1/4096 + 1/16384…

Which equals 1/3. This becomes important when you see the use made of the shape in Stewart’s book. The unicorn triangle is a rep-tile, or a shape that can be divided into smaller copies of the same shape:

An equilateral triangle can be divided into four copies of itself, each 1/4 of the original area. If an equilateral triangle with an area of 4 is divided into three unicorn triangles, each unicorn has an area of 1 + 1/3 and 3 * (1 + 1/3) = 4.

Because it’s a rep-tile, a unicorn triangle is also a fractal, a shape that is self-similar at smaller and smaller scales. When one of the sub-unicorns is dropped, the fractals become more obvious:

$unicorn_fractal1$

$unicorn_fractal2$

$unicorn_fractal3$

Elsewhere other-posted:

• Rep-Tiles Revisited

Boldly Breaking the Boundaries

Thursday, 21st May, 2015 by Krilling for Company in Fractals, Geometry, Mathematics, Rep-Tiles and tagged block fractals, divide-and-discard, fractal, fractal geometry, fractals, fractals based on squares, geometry, hexagonal fractal, math, mathematics, maths, much in little, over-fractals, recreational math, recreational mathematics, recreational maths, square, Squares | Leave a comment

In “M.I.P. Trip”, I looked at fractals like this, in which a square is divided repeatedly into a pattern of smaller squares:

As you can see, the sub-squares appear within the bounds of the original square. But what if some of the sub-squares appear beyond the bounds of the original square? Then a new family of fractals is born, the over-fractals:

Hex Appeal

Tuesday, 7th Jan, 2014 by Krilling for Company in Geometry, Mathematics, Rep-Tiles and tagged animated gif, animated gifs, double-triangle, equilateral triangle, equilateral triangles, fish rep-tile, fish rep-tiles, five sides, five vertices, four right triangles, geometric, geometric dissection, geometric dissections, geometry, Great Sphinx at Giza, hexiamonds, isosceles right triangle, isosceles right triangles, math, mathematics, maths, pentagon, pentagonal rep-tile, pentagonal rep-tiles, Pentagons, polyiamond, polyiamonds, polyshape, polyshapes, recreational math, recreational mathematics, recreational maths, rep-4 sphinx, rep-9 sphinx, rep-tile, Rep-Tiles, right triangle, right triangles, self-replication, sphinx, sphinx hexiamond, tessellation, tessellations, three equilateral triangles, tiling, tilings, triangle, Triangles, vertex | Leave a comment

A polyiamond is a shape consisting of equilateral triangles joined edge-to-edge. There is one moniamond, consisting of one equilateral triangle, and one diamond, consisting of two. After that, there are one triamond, three tetriamonds, four pentiamonds and twelve hexiamonds. The most famous hexiamond is known as the sphinx, because it’s reminiscent of the Great Sphinx of Giza:

The Great Sphinx of Giza

It’s famous because it is the only known pentagonal rep-tile, or shape that can be divided completely into smaller copies of itself. You can divide a sphinx into either four copies of itself or nine copies, like this (please open images in a new window if they fail to animate):

So far, no other pentagonal rep-tile has been discovered. Unless you count this double-triangle as a pentagon:

It has five sides, five vertices and is divisible into sixteen copies of itself. But one of the vertices sits on one of the sides, so it’s not a normal pentagon. Some might argue that this vertex divides the side into two, making the shape a hexagon. I would appeal to these ancient definitions: a point is “that which has no part” and a line is “a length without breadth” (see Neuclid on the Block). The vertex is a partless point on the breadthless line of the side, which isn’t altered by it.

But, unlike the sphinx, the double-triangle has two internal areas, not one. It can be completely drawn with five continuous lines uniting five unique points, but it definitely isn’t a normal pentagon. Even less normal are two more rep-tiles that can be drawn with five continuous lines uniting five unique points: the fish that can be created from three equilateral triangles and the fish that can be created from four isosceles right triangles:

Rep It Up

Tuesday, 17th Dec, 2013 by Krilling for Company in Geometry, Mathematics, Rep-Tiles and tagged animated gifs, equilateral triangle, equilateral triangles, geometric, geometric dissection, geometric dissections, geometry, isosceles right triangle, isosceles right triangles, math, mathematics, maths, polyiamond, polyiamonds, polyshape, polyshapes, recreational math, recreational mathematics, recreational maths, rep-tile, Rep-Tiles, right triangle, right triangles, self-replication, tessellation, tessellations, tiling, tilings, triangle, Triangles, twelve equilateral triangles | Leave a comment

When I started to look at rep-tiles, or shapes that can be divided completely into smaller copies of themselves, I wanted to find some of my own. It turns out that it’s easy to automate a search for the simpler kinds, like those based on equilateral triangles and right triangles.

(Please open the following images in a new window if they fail to animate)

Previously pre-posted (please peruse):

• Rep-Tile Reflections

Rep-Tile Reflections

Saturday, 23rd Mar, 2013 by Krilling for Company in Astronomy, Geometry, Mathematics, Philosophy, Philosophy of mathematics, Rep-Tiles, Science and tagged alternative realities, alternative reality, √2, Big Bang, Big Crunch, Credo in Piscem Unum et Infinitum et Æternum, double-square, double-triangle, extraterrestrial intelligence, gas-based life, geometric, geometrical, geometry, half-square, hypotenuse, intelligence, intelligent life, math, math-based religion, math-religion, mathematical religion, mathemystic, mathemystic communion, mathemystical, mathemysticism, maths, maths-based religion, mental realm, metaphysical, metaphysics, mind, minds, mystic communism, parallel universe, parallel universes, powers of 9, powers of nine, psycho-math-space, rectangle, rectangles, Religion, rep-tile, Rep-Tiles, rep-triangle, rep-triangles, repeat-tile, repeat-tiles, repeating tile, repeating tiles, repetition-tile, repetition-tiles, right triangle, silicon-based life, speculation, speculatory, square, square root of 2, square root of two, Squares, tessellate, tessellation, tessellations, the fish, the sphinx, trans-biological communion, triangle, Triangles, universe | 5 Comments

A rep-tile, or repeat-tile, is a two-dimensional shape that can be divided completely into copies of itself. A square, for example, can be divided into smaller squares: four or nine or sixteen, and so on. Rectangles are the same. Triangles can be divided into two copies or three or more, depending on their precise shape. Here are some rep-tiles, including various rep-triangles:

Various rep-tiles — click for larger image

Some are simple, some are complex. Some have special names: the sphinx and the fish are easy to spot. I like both of those, particularly the fish. It would make a good symbol for a religion: richly evocative of life, eternally sub-divisible of self: 1, 9, 81, 729, 6561, 59049, 531441… I also like the double-square, the double-triangle and the T-tile in the top row. But perhaps the most potent, to my mind, is the half-square in the bottom left-hand corner. A single stroke sub-divides it, yet its hypotenuse, or longer side, represents the mysterious and mind-expanding √2, a number that exists nowhere in the physical universe. But the half-square itself is mind-expanding. All rep-tiles are. If intelligent life exists elsewhere in the universe, perhaps other minds are contemplating the fish or the sphinx or the half-square and musing thus: “If intelligent life exists elsewhere in the universe, perhaps…”

Mathematics unites human minds across barriers of language, culture and politics. But perhaps it unites minds across barriers of biology too. Imagine a form of life based on silicon or gas, on unguessable combinations of matter and energy in unreachable, unobservable parts of the universe. If it’s intelligent life and has discovered mathematics, it may also have discovered rep-tiles. And it may be contemplating the possibility of other minds doing the same. And why confine these speculations to this universe and this reality? In parallel universes, in alternative realities, minds may be contemplating rep-tiles and speculating in the same way. If our universe ends in a Big Crunch and then explodes again in a Big Bang, intelligent life may rise again and discover rep-tiles again and speculate again on their implications. The wildest speculation of all would be to hypothesize a psycho-math-space, a mental realm beyond time and matter where, in mathemystic communion, suitably attuned and aware minds can sense each other’s presence and even communicate.

Credo in Piscem…

So meditate on the fish or the sphinx or the half-square. Do you feel the tendrils of an alien mind brush your own? Are you in communion with a stone-being from the far past, a fire-being from the far future, a hive-being from a parallel universe? Well, probably not. And even if you do feel those mental tendrils, how would you know they’re really there? No, I doubt that the psycho-math-space exists. But it might and science might prove its existence one day. Another possibility is that there is no other intelligent life, never has been, and never will be. We may be the only ones who will ever muse on rep-tiles and other aspects of mathematics. Somehow, though, rep-tiles themselves seem to say that this isn’t so. Particularly the fish. It mimics life and can spawn itself eternally. As I said, it would make a good symbol for a religion: a mathemysticism of trans-biological communion. Credo in Piscem, Unum et Infinitum et Æternum. “I believe in the Fish, One, Unending, Everlasting.” That might be the motto of the religion. If you want to join it, simply wish upon the fish and muse on other minds, around other stars, who may be doing the same.

Rep-Tiles Revisited

Friday, 26th Oct, 2012 by Krilling for Company in Fractals, Mathematics, Rep-Tiles and tagged animated gif, animated gifs, fractal, fractals, geometry, L-tromino, math, mathematics, maths, rep-tile, Rep-Tiles, tromino | Leave a comment

Pre-Previously Posted (Please Peruse)

A Feast of Fractiles

Thursday, 11th Oct, 2012 by Krilling for Company in Fractals, Mathematics, Our Lady of the Gutter, Rep-Tiles and tagged fractal, fractal geometry, fractal triangle, fractal triangles, fractals, geometry, math, mathematics, maths, Our Lady of the Gutter, triangle, Triangles | Leave a comment

A rep-tile is a shape that can be divided into copies of itself. One of the simplest rep-tiles is the equilateral triangle, which can be divided into four copies of itself, like this:

If, on the other hand, the triangle is subdivided and then one of the copies is discarded, many interesting fractals can be made from this very simple shape:

$Triangle fractal 2$

This sequence illustrates how a more complex fractal is created:

$Triangle fractal 3 split image 1$

$Triangle fractal 3 split image 2$

$Triangle fractal 3 split image 3$

$Triangle fractal 3 split image 4$

$Triangle fractal 3 split image 5$

$Triangle fractal 3 split image 6$

$Triangle fractal 3 split image 7$

$Triangle fractal 3 split image 8$

And here is the sequence in a single animated gif:

$Triangle fractal 10$

$Triangle fractal 11$

$Triangle fractal 12$

$Triangle fractal 13$

$Triangle fractal 15$

$Triangle fractal 16$

$Triangle fractal 17$

$Triangle fractal 18$

$Triangle fractal 19$

$Triangle fractal 20$

$Triangle fractal 21$

$Triangle fractal 22$

$Triangle fractal 23$

$Triangle fractal 24$

$Triangle fractal 25$

$Triangle fractal 26$

Overlord In Terms of Core Issues Around Maximal Engagement with Key Notions of the Über-Feral

მეფე (2) • მსოფლიოს (3) • მათემატიკა (5) •

Category Archives: Rep-Tiles