Tag Archives: geometry

We Can Circ It Out

by in Circles, Fractals, Geometry, Mathematics, Polygons, Squares, Triangles and tagged , , , , , , , , , , , , , , | Leave a comment

It’s a pretty little problem to convert this triangular fractal…

Sierpiński triangle (Wikipedia)

…into its circular equivalent:

Sierpiński triangle as circle

Sierpiński triangle to circle (animated)

But once you’ve circ’d it out, as it were, you can easily adapt the technique to fractals based on other polygons:

T-square fractal (Wikipedia)
⇓

T-square fractal as circle

T-square fractal to circle (animated)

Elsewhere other-accessible…

• Dilating the Delta — more on converting polygonic fractals to circles…

The Belles of El

by in Geometry, History, Language, Mathematics and tagged , , , , , , , , , , , , , , , , , , , , | Leave a comment

Title page of Sir Henry Billingsley’s first English version of Euclid’s Elements, 1570, with personifications of Geometria, Astronomia, Arithmetica and Musica as beautiful young women

The Elements of Geometrie of the Moſt Aucient Philoſopher Evclide of Megara.

Faithfully (now first) tranʃlated into the Engliʃhe toung, by H. Billingſley, Citizen of London.

Whereunto are annexed certaine Scolies, Annotations, and Inuentions, of the best Mathematiciens, both of times past, and in this our age.

With a very fruitfull Præface made by M.I. Dee, ʃpecifying the chiefe Mathematicall Sciences, what they are, and wherunto commodious: where, alʃo, are diʃcloʃed certaine new Secrets Mathematicall and Mechanicall, untill theʃe our daies, greatly miʃʃed.

Imprinted at London by Iohn Daye.

The title of this incendiary intervention is a paronomasia on “The Bells of Hell…”, a British airmen’s song in terms of core issues around World War I.

Game of Throwns

by in Chaos Game, Fractals, Geometry, Mathematics, Squares, Triangles and tagged , , , , , , , , , , , , | Leave a comment

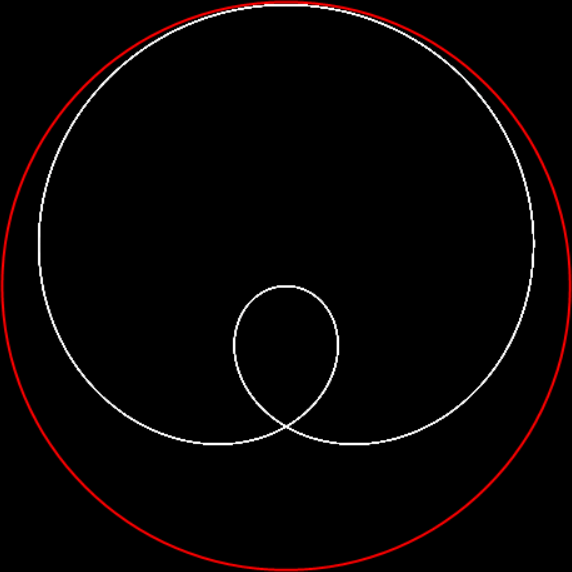
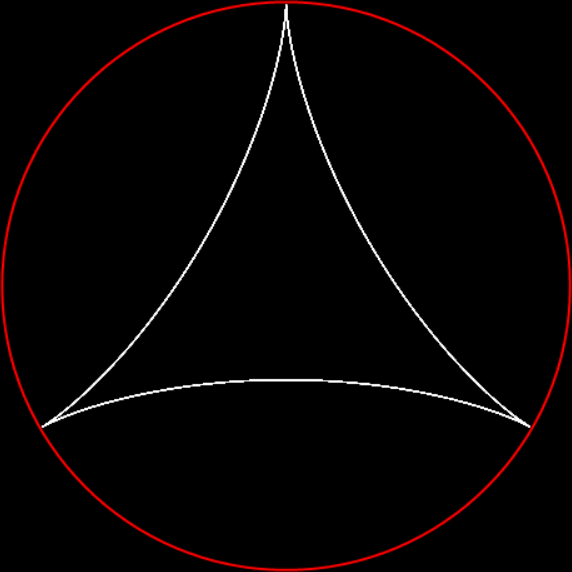
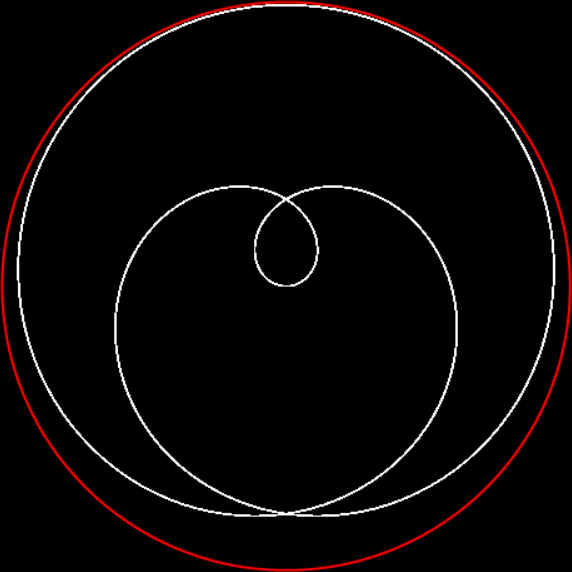
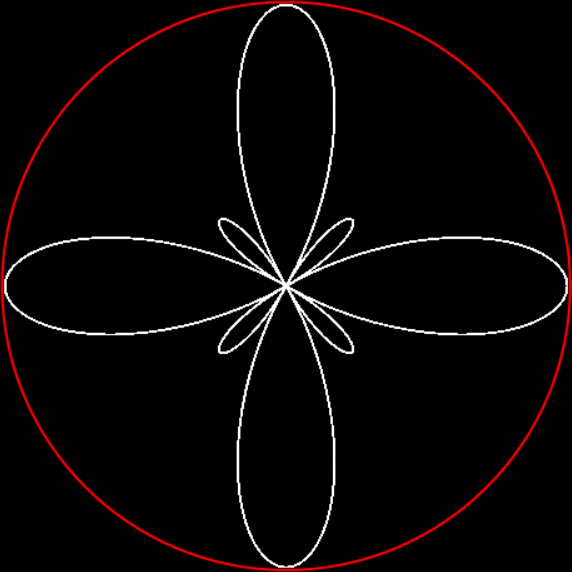
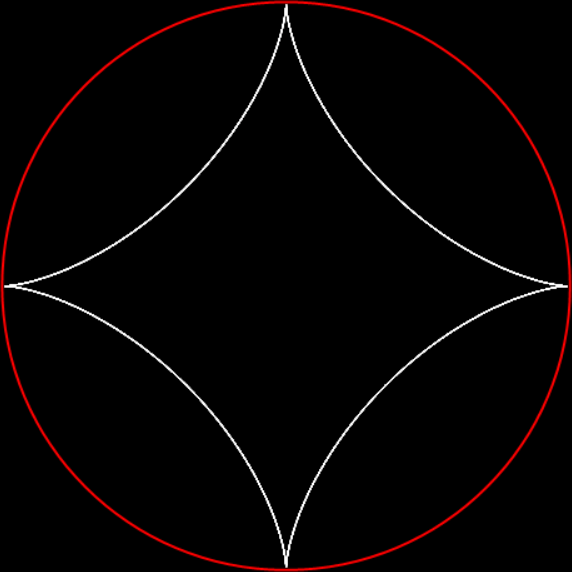
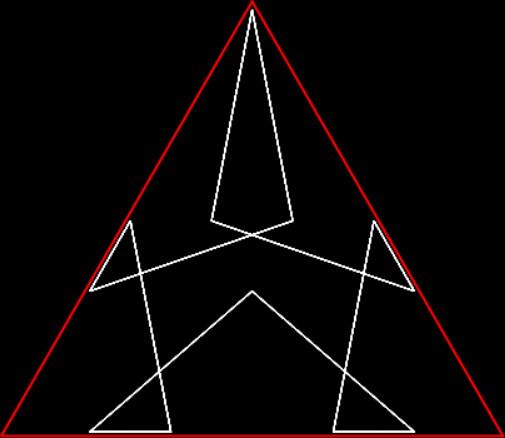
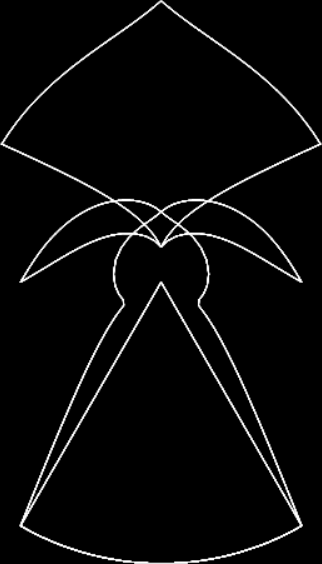
In “Scaffscapes”, I looked at these three fractals and described how they were in a sense the same fractal, even though they looked very different:

Fractal #1

Fractal #2

Fractal #3

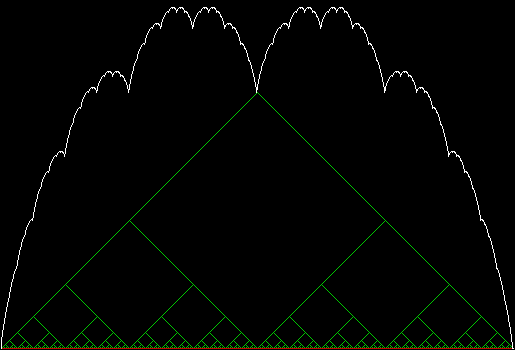
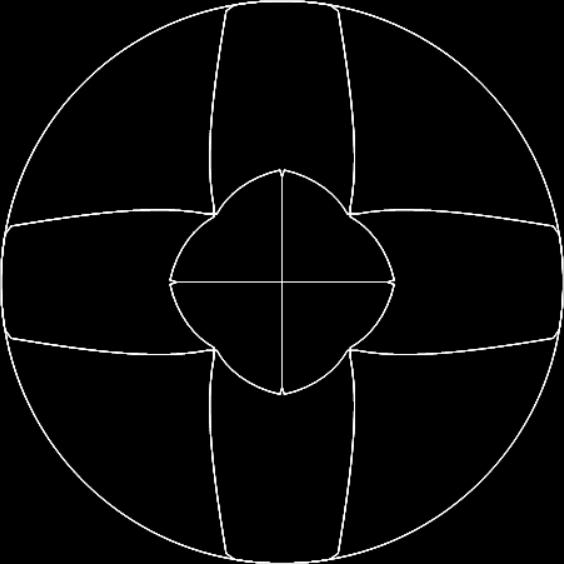
But even if they are all the same in some mathematical sense, their different appearances matter in an aesthetic sense. Fractal #1 is unattractive and seems uninteresting:

Fractal #1, unattractive, uninteresting and unnamed

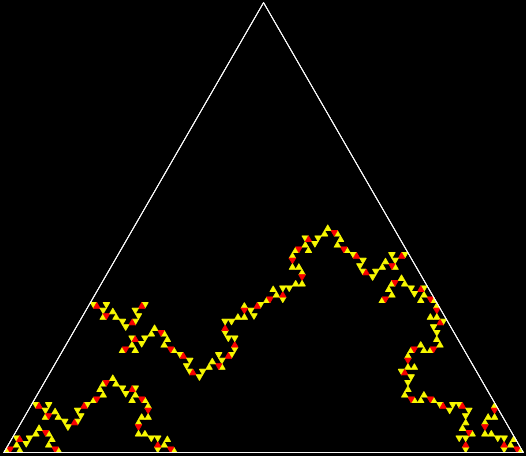
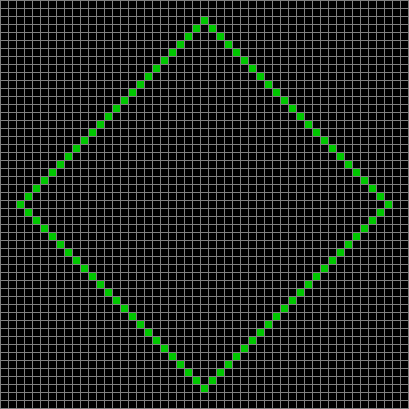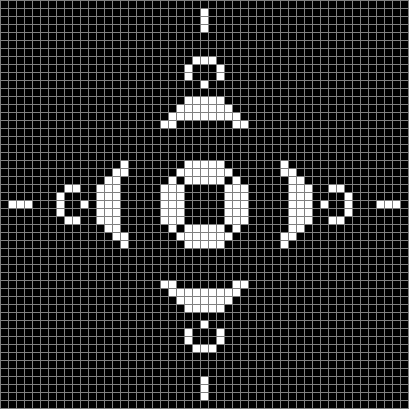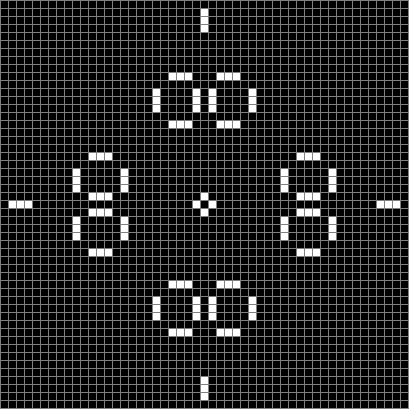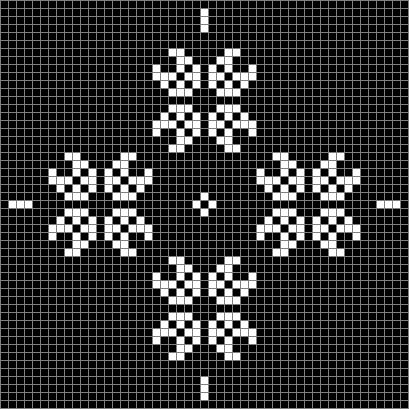
Fractal #3 is attractive and interesting. That’s part of why mathematicians have given it a name, the T-square fractal:

Fractal #3 — the T-square fractal

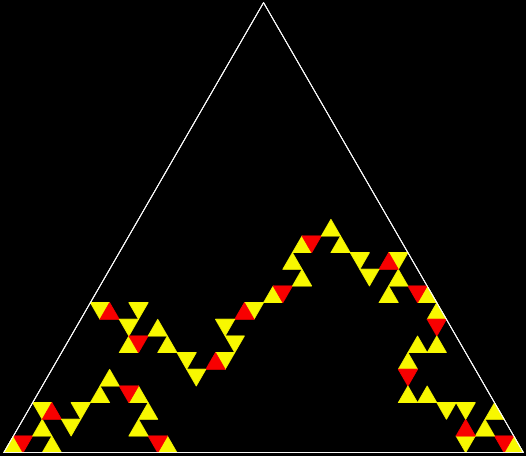
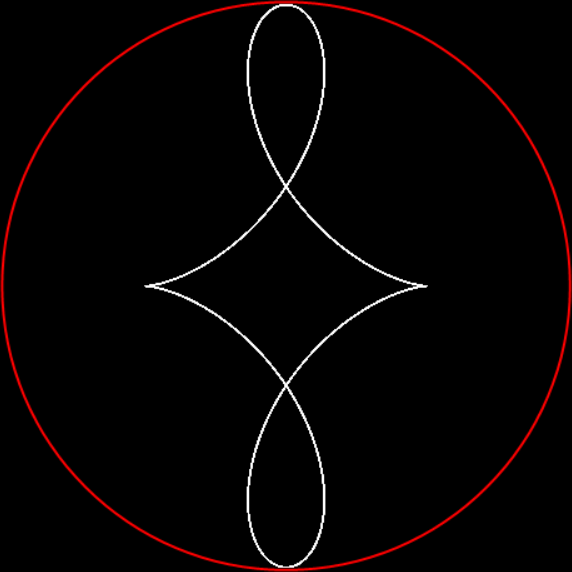
But fractal #2, although it’s attractive and interesting, doesn’t have a name. It reminds me of a ninja throwing-star or shuriken, so I’ve decided to call it the throwing-star fractal or ninja-star fractal:

Fractal #2, the throwing-star fractal

A ninja throwing-star or shuriken

This is one way to construct a throwing-star fractal:

Throwing-star fractal, stage 1

Throwing-star fractal, #2

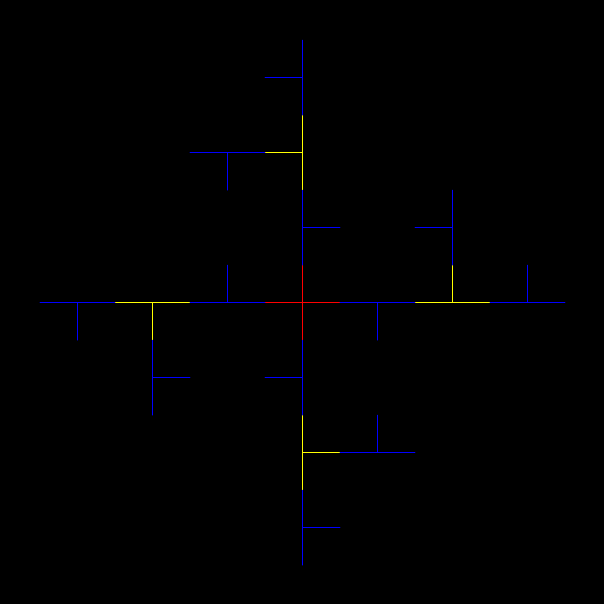
Throwing-star fractal, #3

Throwing-star fractal, #4

Throwing-star fractal, #5

Throwing-star fractal, #6

Throwing-star fractal, #7

Throwing-star fractal, #8

Throwing-star fractal, #9

Throwing-star fractal, #10

Throwing-star fractal, #11

Throwing-star fractal (animated)

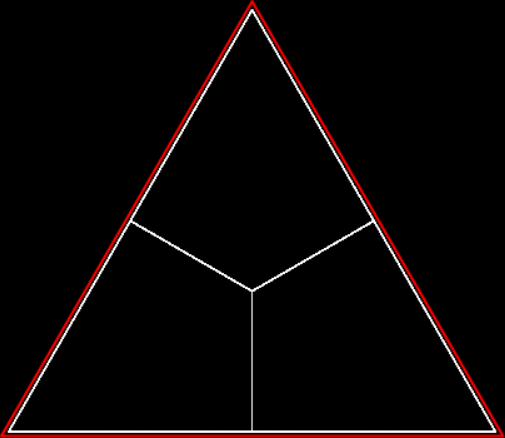
But there’s another way to construct a throwing-star fractal. You use what’s called the chaos game. To understand the commonest form of the chaos game, imagine a ninja inside an equilateral triangle throwing a shuriken again and again halfway towards a randomly chosen vertex of the triangle. If you mark each point where the shuriken lands, you eventually get a fractal called the Sierpiński triangle:

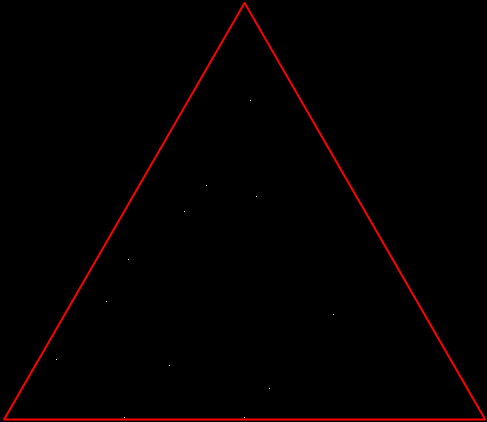
Chaos game with triangle stage 1

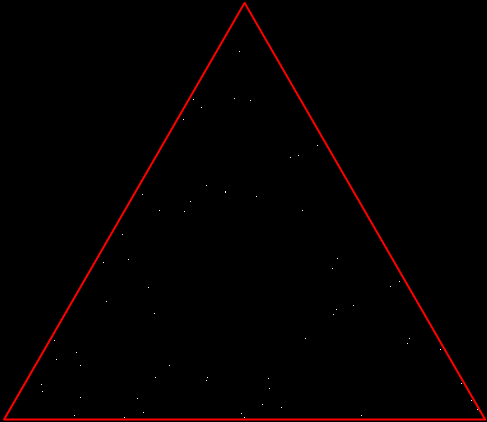
Chaos triangle #2

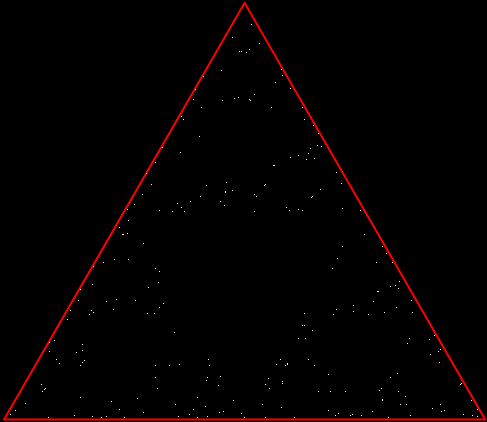
Chaos triangle #3

Chaos triangle #4

Chaos triangle #5

Chaos triangle #6

Chaos triangle #7

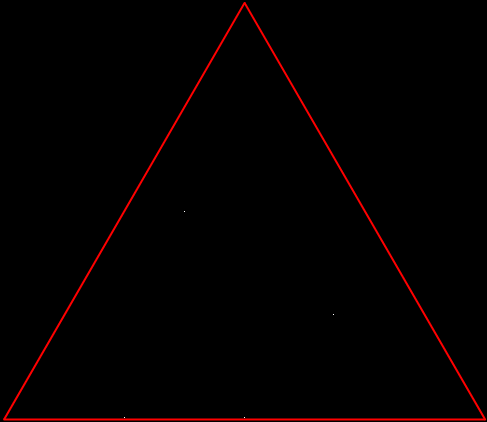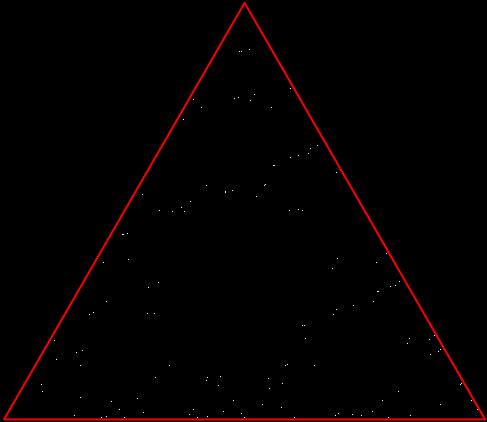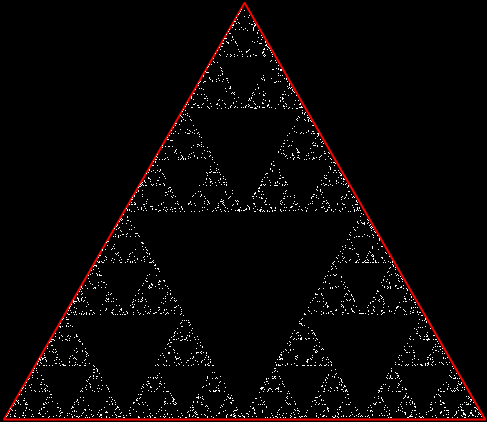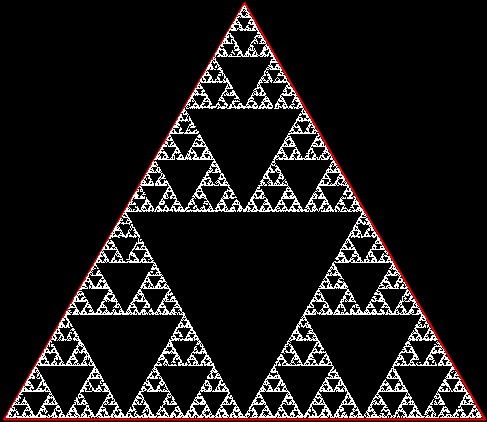
Chaos triangle (animated)

When you try the chaos game with a square, with the ninja throwing the shuriken again and again halfway towards a randomly chosen vertex, you don’t get a fractal. The interior of the square just fills more or less evenly with points:

Chaos game with square, stage 1

Chaos square #2

Chaos square #3

Chaos square #4

Chaos square #5

Chaos square #6

Chaos square (anim)

But suppose you restrict the ninja’s throws in some way. If he can’t throw twice or more in a row towards the same vertex, you get a familiar fractal:

Chaos game with square, ban on throwing towards same vertex, stage 1

Chaos square, ban = v+0, #2

Chaos square, ban = v+0, #3

Chaos square, ban = v+0, #4

Chaos square, ban = v+0, #5

Chaos square, ban = v+0, #6

Chaos square, ban = v+0 (anim)

But what if the ninja can’t throw the shuriken towards the vertex one place anti-clockwise of the vertex he’s just thrown it towards? Then you get another familiar fractal — the throwing-star fractal:

Chaos square, ban = v+1, stage 1

Chaos square, ban = v+1, #2

Chaos square, ban = v+1, #3

Chaos square, ban = v+1, #4

Chaos square, ban = v+1, #5

Game of Throwns — throwing-star fractal from chaos game (static)

Game of Throwns — throwing-star fractal from chaos game (anim)

And what if the ninja can’t throw towards the vertex two places anti-clockwise (or two places clockwise) of the vertex he’s just thrown the shuriken towards? Then you get a third familiar fractal — the T-square fractal:

Chaos square, ban = v+2, stage 1

Chaos square, ban = v+2, #2

Chaos square, ban = v+2, #3

Chaos square, ban = v+2, #4

Chaos square, ban = v+2, #5

T-square fractal from chaos game (static)

T-square fractal from chaos game (anim)

Finally, what if the ninja can’t throw towards the vertex three places anti-clockwise, or one place clockwise, of the vertex he’s just thrown the shuriken towards? If you can guess what happens, your mathematical intuition is much better than mine.

Post-Performative Post-Scriptum

I am not now and never have been a fan of George R.R. Martin. He may be a good author but I’ve always suspected otherwise, so I’ve never read any of his books or seen any of the TV adaptations.

Scaffscapes

by in Fractals, Geometry, Mathematics, Squares and tagged , , , , , , , , , | Leave a comment

A fractal is a shape that contains copies of itself on smaller and smaller scales. You can find fractals everywhere in nature. Part of a fern looks like the fern as a whole:

Fern as fractal (source)

Part of a tree looks like the tree as a whole:

Tree as fractal (source)

Part of a landscape looks like the landscape as a whole:

Landscape as fractal (source)

You can also create fractals for yourself. Here are three that I’ve constructed:

Fractal #1

Fractal #2

Fractal #3 — the T-square fractal

The three fractals look very different and, in one sense, that’s exactly what they are. But in another sense, they’re the same fractal. Each can morph into the other two:

Fractal #1 → fractal #2 → fractal #3 (animated)

Here are two more fractals taken en route from fractal #2 to fractal #3, as it were:

Fractal #4

Fractal #5

To understand how the fractals belong together, you have to see what might be called the scaffolding. The construction of fractal #3 is the easiest to understand. First you put up the scaffolding, then you take it away and leave the final fractal:

Fractal #3, scaffolding stage 1

Fractal #3, stage 2

Fractal #3, stage 3

Fractal #3, stage 4

Fractal #3, stage 5

Fractal #3, stage 6

Fractal #3, stage 7

Fractal #3, stage 8

Fractal #3, stage 9

Fractal #3, stage 10

Fractal #3 (scaffolding removed)

Construction of fractal #3 (animated)

Now here’s the construction of fractal #1:

Fractal #1, stage 1

Fractal #1, stage 2

Fractal #1, stage 3

↓

Construction of fractal #1 (animated)

Fractal #1 (static)

And the constructions of fractals #2, #4 and #5:

Fractal #2, stage 1

Fractal #2, stage 2

Fractal #2, stage 3

↓

Fractal #2 (animated)

Fractal #2 (static)

Fractal #4, stage 1

Fractal #4, stage 2

Fractal #4, stage 3

↓

Fractal #4 (animated)

Fractal #4 (static)

Fractal #5, stage 1

Fractal #5, stage 2

Fractal #5, stage 3

↓

Fractal #5 (animated)

Fractal #5

Twi-Phi

by in Fractals, Geometry, φ, Mathematics, Pentagons, Phi and tagged , , , , , , , , , , , , , , | Leave a comment

Here’s a pentagon:

Stage #1

And here’s the pentagon with smaller pentagons on its vertices:

Stage #2

And here’s more of the same:

Stage #3

Stage #4

Stage #5

Stage #6

Stage #7

Stage #8

Animated fractal

At infinity, the smaller pentagons have reached out like arms to exactly fill the gaps between themselves without overlapping. But how much smaller is each set of smaller pentagons than its mother-pentagon when the gaps are exactly filled? Well, if the radius of the mother-pentagon is r, then the radius of each daughter-pentagon is r * 1/(φ^2) = r * 0·38196601125…

But what happens if the radius relationship of mother to daughter is r * 1/φ = r * 0·61803398874 = r * (φ-1)? Then you get this fractal:

Stage #1

Stage #2

Stage #3

Stage #4

Stage #5

Stage #6

Stage #7

Stage #8

Stage #9

Animated fractal

Delta Skelta

by in Fractals, Geometry, Mathematics, Triangles and tagged , , , , , , , , , , , , | Leave a comment

“When I get to the bottom I go back to the top of the slide,
Where I stop and I turn and I go for a ride
Till I get to the bottom and I see you again.” — The Beatles, “Helter Skelter” (1968)

First stage of fractal #1

Animated fractal #1

First stage of fractal #2

Animated fractal #2

See-Saw Jaw

by in Fractals, Geometry, Mathematics and tagged , , , , , , , , , | Leave a comment

From Sierpiński triangle to T-square to Mandibles (and back again) (animated)
(Open in new window if distorted)

Elsewhere other-accessible…

• Mandibular Metamorphosis — explaining the animation above
• Agnathous Analysis — more on the Sierpiński triangle and T-square fractal

Middlemath

by in Chaos Game, Fractals, Geometry, Mathematics, Pentagons, Squares and tagged , , , , , , , , , , , , , , , , | Leave a comment

Suppose you start at the middle of a triangle, then map all possible ways you can jump eight times half-way towards one or another of the vertices of the triangle. At the end of the eight jumps, you mark your final position with a dot. You could jump eight times towards the same vertex, or once towards vertex 1, once towards vertex 2, and once again towards vertex 1. And so on. If you do this, the record of your jumps looks something like this:

The shape is a fractal called the Sierpiński triangle. But if you try the same thing with a square — map all possible jumping-routes you can follow towards one or another of the four vertices — you simply fill the interior of the square. There’s no interesting fractal:

So you need a plan with a ban. Try mapping all possible routes where you can’t jump towards the same vertex twice in a row. And you get this:

Ban on jumping towards same vertex twice in a row, v(t) ≠ v(t-1)

If you call the current vertex v(t) and the previous vertex v(t-1), the ban says that v(t) ≠ v(t-1). Now suppose you can’t jump towards the vertex one place clockwise of the previous vertex. Now the ban is v(t)-1 ≠ v(t-1) or v(t) ≠ v(t-1)+1 and this fractal appears:

v(t) ≠ v(t-1)+1

And here’s a ban on jumping towards the vertex two places clockwise (or counterclockwise) of the vertex you’ve just jumped towards:

v(t) ≠ v(t-1)+2

And finally the ban on jumping towards the vertex three places clockwise (or one place counterclockwise) of the vertex you’ve just jumped towards:

v(t) ≠ v(t-1)+3 (a mirror-image of v(t) ≠ v(t-1)+1, as above)

Now suppose you introduce a new point to jump towards at the middle of the square. You can create more fractals, but you have to adjust the kind of ban you use. The central point can’t be included in the ban or the fractal will be asymmetrical. So you continue taking account of the vertices, but if the previous jump was towards the middle, you ignore that jump. At least, that’s what I intended, but I wonder whether my program works right. Anyway, here are some of the fractals that it produces:

v(t) ≠ v(t-1) with central point (wcp)

v(t) ≠ v(t-1)+1, wcp

v(t) ≠ v(t-1)+2, wcp

And here are some bans taking account of both the previous vertex and the pre-previous vertex:

v(t) ≠ v(t-1) & v(t) ≠ v(t-2), wcp

v(t) ≠ v(t-1) & v(t-2)+1, wcp

v(t) ≠ v(t-1)+2 & v(t-2), wcp

v(t) ≠ v(t-1) & v(t-2)+1, wcp

v(t) ≠ v(t-1)+1 & v(t-2)+1, wcp

v(t) ≠ v(t-1)+2 & v(t-2)+1, wcp

v(t) ≠ v(t-1)+3 & v(t-2)+1, wcp

v(t) ≠ v(t-1) & v(t-2)+2, wcp

v(t) ≠ v(t-1)+1 & v(t-2)+2, wcp

v(t) ≠ v(t-1)+2 & v(t-2)+2, wcp

Now look at pentagons. They behave more like triangles than squares when you map all possible jumping-routes towards one or another of the five vertices. That is, a fractal appears:

All possible jumping-routes towards the vertices of a pentagon

But the pentagonal-jump fractals get more interesting when you introduce jump-bans:

v(t) ≠ v(t-1)

v(t) ≠ v(t-1)+1

v(t) ≠ v(t-1)+2

v(t) ≠ v(t-1) & v(t-2)

v(t) ≠ v(t-1)+2 & v(t-2)

v(t) ≠ v(t-1)+1 & v(t-2)+1

v(t) ≠ v(t-1)+3 & v(t-2)+1

v(t) ≠ v(t-1)+1 & v(t-2)+2

v(t) ≠ v(t-1)+2 & v(t-2)+2

v(t) ≠ v(t-1)+3 & v(t-2)+2

Finally, here are some pentagonal-jump fractals using a central point:

Post-Performative Post-Scriptum

I’m not sure if I’ve got the order of some bans right above. For example, should v(t) ≠ v(t-1)+1 & v(t-2)+2 really be v(t) ≠ v(t-1)+2 & v(t-2)+1? I don’t know and I’m not going to check. But the idea of jumping-point bans is there and that’s all you need if you want to experiment with these fractal methods for yourself.

Six Mix Trix

by in Circles, Fractals, Geometry, Mathematics, Triangles and tagged , , , , , , , , , , , , , , , , | Leave a comment

Here’s an equilateral triangle divided into six smaller triangles:

Equilateral triangle divided into six irregular triangles (Stage #1)

Now keep on dividing:

Stage #2

Stage #3

Stage #4

Stage #5

Equilateral triangle dividing into six irregular triangles (animated)

But what happens if you divide the triangle, then discard some of the sub-triangles, then repeat? You get a self-similar shape called a fractal:

Divide-and-discard stage #1

Stage #2

Stage #3

Stage #4

Stage #5

Stage #6

Triangle fractal (animated)

Here’s another example:

Divide-and-discard stage #1

Stage #2

Stage #3

Stage #4

Stage #5

Stage #6

Stage #7

Triangle fractal (animated)

You can also delay the divide-and-discard to create a more symmetrical fractal, like this:

Delayed divide-and-discard stage #1

Stage #2

Stage #3

Stage #4

Stage #5

Stage #6

Stage #7

Triangle fractal (animated)

What next? You can use trigonometry to turn the cramped triangle into a circle:

Triangular fractal

⇓

Circular fractal
(Open in new window for full image)

Triangle-to-circle (animated)

Here’s another example:

Triangular fractal

⇓

Circular fractal

Triangle-to-circle (animated)

And below are some more circular fractals converted from triangular fractals. Some of them look like distorted skulls or transdimensional Lovecraftian monsters:

(Open in new window for full image)

Previous Pre-Posted

• Circus Trix — an earlier look at sextally-divided-equilateral-triangle fractals