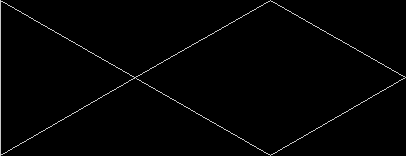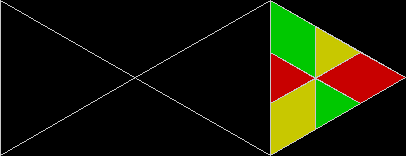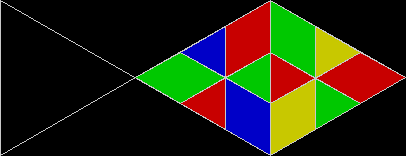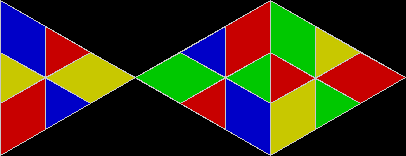
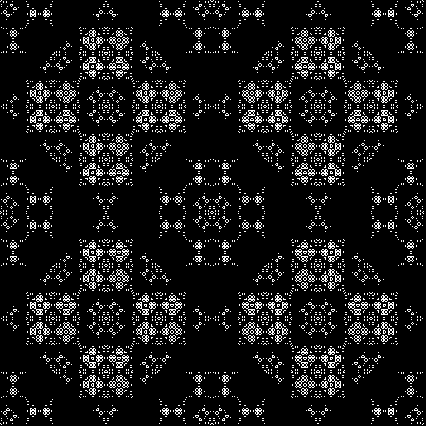Arty Fish Haul

Saturday, 11th May, 2024 by Krilling for Company in Fractals, Mathematics, Triangles and tagged animated gifs, animated gifs of fractals, fractal animation, fractal dish, fractal geometry, isosceles right triangles, recreational math, recreational mathematics, recreational maths | Leave a comment

When is a fish a reptile? When it looks like this:

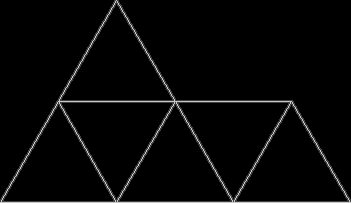
Fish from four isosceles right triangles

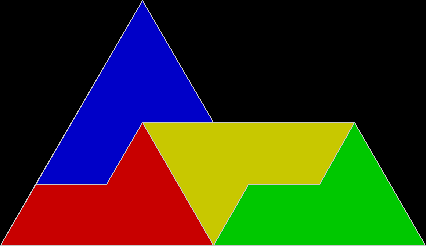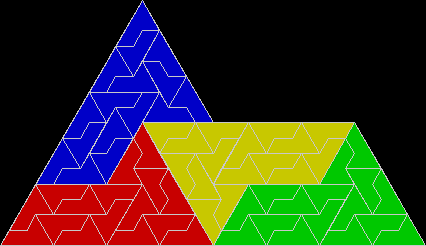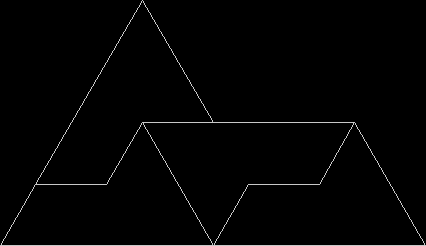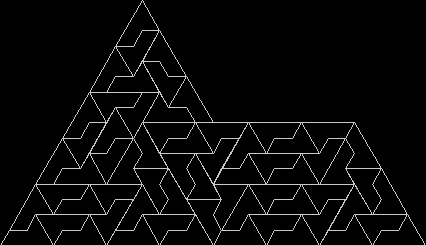
The fish-shape can be divided into eight identical sub-copies of itself. That is, it can be repeatedly tiled with copies of itself, so it’s an example of what geometry calls a rep-tile:

Fish divided into eight identical sub-copies

Fish divided again

Fish divided #4

Fish divided #5

Fish divided #6

Fish (animated rep-tiling)

Now suppose you divide the fish, then discard one of the sub-copies. And carry on dividing-and-discarding like that:

Fish discarding sub-copy 7 (#1)

Fish discarding sub-copy 7 (#2)

Fish discarding sub-copy 7 (#3)

Fish discarding sub-copy 7 (#4)

Fish discarding sub-copy 7 (#5)

Fish discarding sub-copy 7 (#6)

Fish discarding sub-copy 7 (#7)

Fish discarding sub-copy 7 (animated)

Here are more examples of the fish sub-dividing, then discarding sub-copies:

Fish discarding sub-copy #1

Fish discarding sub-copy #2

Fish discarding sub-copy #3

Fish discarding sub-copy #4

Fish discarding sub-copy #5

Fish discarding sub-copy #6

Fish discarding sub-copy #7

Fish discarding sub-copy #8

Fish discarding sub-copies (animated)

Now try a square divided into four copies of the fish, then sub-divided again and again:

Fish-square #1

Fish-square #2

Fish-square #3

Fish-square #4

Fish-square #5

Fish-square #6

Fish-square (animated)

The fish-square can be used to create more symmetrical patterns when the divide-and-discard rule is applied. Here’s the pattern created by dividing-and-discarded two of the sub-copies:

Fish-square divide-and-discard #1

Fish-square divide-and-discard #2

Fish-square divide-and-discard #3

Fish-square divide-and-discard #4

Fish-square divide-and-discard #5

Fish-square divide-and-discard #6

Fish-square divide-and-discard #7

Fish-square divide-and-discard #8 (delayed discard)

Fish-square divide-and-discard (animated)

Using simple trigonometry, you can convert the square pattern into a circular pattern:

↓

Circular version

Square to circle (animated)

Here are more examples of divide-and-discard fish-squares:

Fish-square divide-and-discard #1

Fish-square divide-and-discard #2

Fish-square divide-and-discard #3

Fish-square divide-and-discard #4

Fish-square divide-and-discard #5

Fish-square divide-and-discard #6

And more examples of fish-squares being converted into circles:

Fish-square to circle #1 (animated)

Fish-square to circle #2

Fish-square to circle #3

Fish-square to circle #4

Fish-square to circle #5

Fish-square to circle #6

Tri Again (Again)

Friday, 3rd Feb, 2017 by Krilling for Company in Fractals, Geometry, Mathematics, Rep-Tiles and tagged animated gif, animated gifs, crane fractal, fractal, fractal geometry, fractals, fractals from triangles, geometry, hourglass fractal, isosceles right triangles, isosceles triangles, math, mathematics, maths, mirror symmetry, mirror-symmetrical, recreational math, recreational mathematics, recreational maths, right triangles, simple fractals, Triangles | Leave a comment

I didn’t expect to find the hourglass fractal playing with squares. I even less expected it playing with triangles. Isosceles right triangles, to be precise. Then again, I found it first playing with the L-triomino, which is composed of three squares. And an isosceles triangle is half of a square. So it all fits. This is an isosceles right triangle:

Isosceles right triangle

It’s mirror-symmetrical, so it looks the same in a mirror unless you label one of the acute-angled corners in some way, like this:

right_triangle_chiral_1

Right triangle with labelled corner

right_triangle_chiral_2

Right triangle reflected

Reflection is how you find the hourglass fractal. First, divide a right triangle into four smaller right triangles.

Right triangle rep-tiled

Then discard one of the smaller triangles and repeat. If the acute corners of the smaller triangles have different orientations, one of the permutations creates the hourglass fractal, like this:

Hourglass #1

Hourglass #2

Hourglass #3

Hourglass #4

Hourglass #5

Hourglass #6

Hourglass #7

Hourglass #8

Hourglass #9

Hourglass animated

Another permutation of corners creates what I’ve decided to call the crane fractal, like this:

Crane fractal animated

Crane fractal (static)

The crane fractal is something else that I first found playing with the L-triomino:

l-triomino_234

Crane fractal from L-triomino

Previously pre-posted:

• Square Routes
• Tri Again

Hex Appeal

Tuesday, 7th Jan, 2014 by Krilling for Company in Geometry, Mathematics, Rep-Tiles and tagged animated gif, animated gifs, double-triangle, equilateral triangle, equilateral triangles, fish rep-tile, fish rep-tiles, five sides, five vertices, four right triangles, geometric, geometric dissection, geometric dissections, geometry, Great Sphinx at Giza, hexiamonds, isosceles right triangle, isosceles right triangles, math, mathematics, maths, pentagon, pentagonal rep-tile, pentagonal rep-tiles, Pentagons, polyiamond, polyiamonds, polyshape, polyshapes, recreational math, recreational mathematics, recreational maths, rep-4 sphinx, rep-9 sphinx, rep-tile, Rep-Tiles, right triangle, right triangles, self-replication, sphinx, sphinx hexiamond, tessellation, tessellations, three equilateral triangles, tiling, tilings, triangle, Triangles, vertex | Leave a comment

A polyiamond is a shape consisting of equilateral triangles joined edge-to-edge. There is one moniamond, consisting of one equilateral triangle, and one diamond, consisting of two. After that, there are one triamond, three tetriamonds, four pentiamonds and twelve hexiamonds. The most famous hexiamond is known as the sphinx, because it’s reminiscent of the Great Sphinx of Giza:

The Great Sphinx of Giza

It’s famous because it is the only known pentagonal rep-tile, or shape that can be divided completely into smaller copies of itself. You can divide a sphinx into either four copies of itself or nine copies, like this (please open images in a new window if they fail to animate):

So far, no other pentagonal rep-tile has been discovered. Unless you count this double-triangle as a pentagon:

It has five sides, five vertices and is divisible into sixteen copies of itself. But one of the vertices sits on one of the sides, so it’s not a normal pentagon. Some might argue that this vertex divides the side into two, making the shape a hexagon. I would appeal to these ancient definitions: a point is “that which has no part” and a line is “a length without breadth” (see Neuclid on the Block). The vertex is a partless point on the breadthless line of the side, which isn’t altered by it.

But, unlike the sphinx, the double-triangle has two internal areas, not one. It can be completely drawn with five continuous lines uniting five unique points, but it definitely isn’t a normal pentagon. Even less normal are two more rep-tiles that can be drawn with five continuous lines uniting five unique points: the fish that can be created from three equilateral triangles and the fish that can be created from four isosceles right triangles:

Rep It Up

Tuesday, 17th Dec, 2013 by Krilling for Company in Geometry, Mathematics, Rep-Tiles and tagged animated gifs, equilateral triangle, equilateral triangles, geometric, geometric dissection, geometric dissections, geometry, isosceles right triangle, isosceles right triangles, math, mathematics, maths, polyiamond, polyiamonds, polyshape, polyshapes, recreational math, recreational mathematics, recreational maths, rep-tile, Rep-Tiles, right triangle, right triangles, self-replication, tessellation, tessellations, tiling, tilings, triangle, Triangles, twelve equilateral triangles | Leave a comment

When I started to look at rep-tiles, or shapes that can be divided completely into smaller copies of themselves, I wanted to find some of my own. It turns out that it’s easy to automate a search for the simpler kinds, like those based on equilateral triangles and right triangles.

(Please open the following images in a new window if they fail to animate)

Previously pre-posted (please peruse):

• Rep-Tile Reflections

Overlord In Terms of Core Issues Around Maximal Engagement with Key Notions of the Über-Feral

მეფე (2) • მსოფლიოს (3) • მათემატიკა (5) •

Tag Archives: isosceles right triangles

Arty Fish Haul

Tri Again (Again)

Hex Appeal

Rep It Up