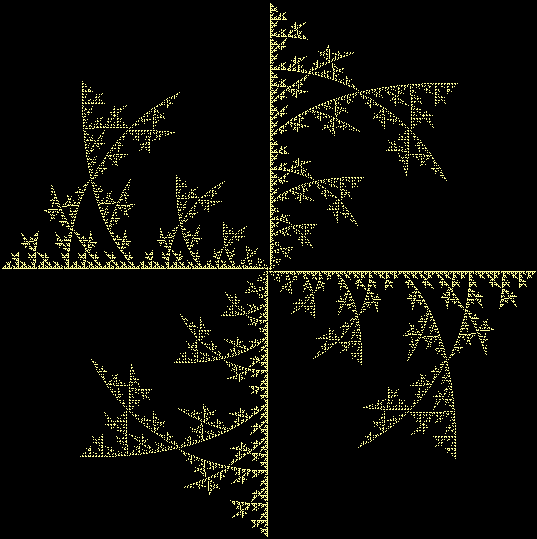Tag Archives: recreational mathematics

Strange “S” in the Light

by in Fractals, Geometry, Mathematics and tagged , , , | Leave a comment

Unexpected discoveries are one of the joys of mathematics, even for amateurs. And computers help you make more of them, because computers make it easy to adjust variables or search faster and further through math-space than any unaided human ever could (on the downside, computers can make you lazy and blunt your intuition). Here’s an unexpected discovery I made using a computer in November 2020:

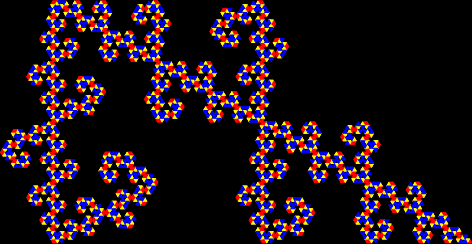
A distorted and dissected capital “S”

It’s a strange “S” that looks complex but is constructed very easily from three simple lines. And it’s a fractal, a shape that contains copies of itself at smaller and smaller scales:

Five sub-fractals of the Strange “S”

Elsewhere Other-Accessible…

• Fractangular Frolics — the Strange “S” in more light

We Can Circ It Out

by in Circles, Fractals, Geometry, Mathematics, Polygons, Squares, Triangles and tagged , , , , , , , , , , , , , , | Leave a comment

It’s a pretty little problem to convert this triangular fractal…

Sierpiński triangle (Wikipedia)

…into its circular equivalent:

Sierpiński triangle as circle

Sierpiński triangle to circle (animated)

But once you’ve circ’d it out, as it were, you can easily adapt the technique to fractals based on other polygons:

T-square fractal (Wikipedia)
⇓

T-square fractal as circle

T-square fractal to circle (animated)

Elsewhere other-accessible…

• Dilating the Delta — more on converting polygonic fractals to circles…

The Devil’s Digits

by in 666, Base Behavior, Mathematics, Number of the Beast and tagged , , , , , , , | Leave a comment

As I’ve said before, I love the way that numbers can come in many different guises. For example, take the number 21. It comes in all these guises:

21 = 10101 in base 2 = 210 in base 3 = 111 in b4 = 41 in b5 = 33 in b6 = 30 in b7 = 25 in b8 = 23 in b9 = 21 in b10 = 1A in b11 = 19 in b12 = 18 in b13 = 17 in b14 = 16 in b15 = 15 in b16 = 14 in b17 = 13 in b18 = 12 in b19 = 11 in b20 = 10 in b21

But I’ve not chosen 21 at random. If you sum the 1s in the representations of 21 in bases 2 to 21, look what you get:

21 = 10101 in base 2 = 210 in base 3 = 111 in b4 = 41 in b5 = 33 in b6 = 30 in b7 = 25 in b8 = 23 in b9 = 21 in b10 = 1A in b11 = 19 in b12 = 18 in b13 = 17 in b14 = 16 in b15 = 15 in b16 = 14 in b17 = 13 in b18 = 12 in b19 = 11 in b20 = 10 in b21

21 = 1s=101s=201s=3 in base 2 = 21s=40 in base 3 = 111s=7 in b4 = 41s=8 in b5 = 33 in b6 = 30 in b7 = 25 in b8 = 23 in b9 = 21s=9 in b10 = 1s=10A in b11 = 1s=119 in b12 = 1s=128 in b13 = 1s=137 in b14 = 1s=146 in b15 = 1s=155 in b16 = 1s=164 in b17 = 1s=173 in b18 = 1s=182 in b19 = 11s=20 in b20 = 1s=210 in b21

In other words, 21 = digcount(21,dig=1,base=2..21). But n = digcount(n,dig,b=2..n) doesn’t happen for any other digit and doesn’t happen often with 1:

3 = digcount(3,d=1,b=2..3) = 11 in b2 = 10 in b3
4 = digcount(4,d=1,b=2..4) = 100 in b2 = 11 in b3 = 10 in b4
6 = digcount(6,d=1,b=2..6) = 110 in b2 = 20 in b3 = 12 in b4 = 11 in b5 = 10 in b6
10 = digcount(10,d=1) = 1010 in b2 = 101 in b3 = 22 in b4 = 20 in b5 = 14 in b6 = 13 in b7 = 12 in b8 = 11 in b9 = 10 in b10
15 = digcount(15,d=1) = 1111 in b2 = 120 in b3 = 33 in b4 = 30 in b5 = 23 in b6 = 21 in b7 = 17 in b8 = 16 in b9 = 15 in b10 = 14 in b11 = 13 in b12 = 12 in b13 = 11 in b14 = 10 in b15
21 = digcount(21,d=1) = 10101 in b2 = 210 in b3 = 111 in b4 = 41 in b5 = 33 in b6 = 30 in b7 = 25 in b8 = 23 in b9 = 21 in b10 = 1A in b11 = 19 in b12 = 18 in b13 = 17 in b14 = 16 in b15 = 15 in b16 = 14 in b17 = 13 in b18 = 12 in b19 = 11 in b20 = 10 in b21

After that, the digcount(n,d=1,b=2..n) → n/2 (see “Digital Dissection” for further discussion). But I decided to look for the first n where digcount(n,dig,b=2..n) = 666:

digcount(1270,1) = 666
digcount(3770,2) = 666
digcount(7667,3) = 666
digcount(12184,4) = 666
digcount(18845,5) = 666
digcount(25806,6) = 666
digcount(34195,7) = 666
digcount(43352,8) = 666
digcount(54693,9) = 666

It doesn’t stop there, of course. You can carry on for ever, looking for digcount(n,A) = 666, digcount(n,B) = 666, digcount(n,C) = 666, where A = 10, B = 11 and C=12, and so on. But it doesn’t start there, either. What about digcount(n,0) = 666? That isn’t easy to find, because 0 usually occurs far less often than other digits in the representation of n. Here are the integers setting records for digcount(n,0,b=2..n):

2 → digcount(2,0) = 1 ← 2= 10 in base 2
4 → digcount(4,0) = 3; ← 4 = 100 in base 2, 11 in base 3, 10 in base 4
8 → digcount(8,0) = 5 ← 8 = 1000 in base 2, 22 in base 3, 20 in base 4, 13 in base 5, 12 in base 6, 11 in base 7, 10 in base 8
12 → digcount(12,0) = 6
16 → digcount(16,0) = 8
18 → digcount(18,0) = 9
32 → digcount(32,0) = 11
36 → digcount(36,0) = 13
64 → digcount(64,0) = 15
72 → digcount(72,0) = 18
128 → digcount(128,0) = 20
144 → digcount(144,0) = 24
252 → digcount(252,0) = 25
264 → digcount(264,0) = 27
288 → digcount(288,0) = 29
360 → digcount(360,0) = 30
504 → digcount(504,0) = 33
540 → digcount(540,0) = 36
720 → digcount(720,0) = 40
900 → digcount(900,0) = 42
1080 → digcount(1080,0) = 47
1680 → digcount(1680,0) = 48
1800 → digcount(1800,0) = 53
2160 → digcount(2160,0) = 56
2520 → digcount(2520,0) = 61
3600 → digcount(3600,0) = 64
4320 → digcount(4320,0) = 66

So what is the first n for which digcount(n,0) = 666? Watch this space.

Reciprocal Recipes

by in Base Behavior, Fibonacci Sequence, Mathematics, Reciprocals and tagged , , , , , , , , , , | Leave a comment

Here’s a sequence. What’s the next number?

1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1...

Here’s another sequence. What’s the next number?

0, 1, 1, 2, 3, 5, 8, 13, 21, 34...

Those aren’t trick questions, so the answers are 1 and 55, respectively. The second sequence is the famous Fibonacci sequence, where each number after [0,1] is the sum of the previous two numbers.

Now try dividing each of those sequences by powers of 2 and summing the results, like this:

1/2 + 1/4 + 1/8 + 1/16 + 1/32 + 1/64 + 1/128 + 1/256 + 1/512 + 1/1024 + 1/2048 + 1/4096 + 1/8192 + 1/16384 + 1/32768 + 1/65536 + 1/131072 + 1/262144 + 1/524288 + 1/1048576 +... = ?

0/2 + 1/4 + 1/8 + 2/16 + 3/32 + 5/64 + 8/128 + 13/256 + 21/512 + 34/1024 + 55/2048 + 89/4096 + 144/8192 + 233/16384 + 377/32768 + 610/65536 + 987/131072 + 1597/262144 + 2584/524288 + 4181/1048576 +... = ?

What are the sums? I was surprised to learn that they’re identical:

1/2 + 1/4 + 1/8 + 1/16 + 1/32 + 1/64 + 1/128 + 1/256 + 1/512 + 1/1024 + 1/2048 + 1/4096 + 1/8192 + 1/16384 + 1/32768 + 1/65536 + 1/131072 + 1/262144 + 1/524288 + 1/1048576 +... = 1

0/2 + 1/4 + 1/8 + 2/16 + 3/32 + 5/64 + 8/128 + 13/256 + 21/512 + 34/1024 + 55/2048 + 89/4096 + 144/8192 + 233/16384 + 377/32768 + 610/65536 + 987/131072 + 1597/262144 + 2584/524288 + 4181/1048576 +... = 1

I discovered this when I was playing with an old scientific calculator and calculated these sums:

5^2 + 2^2 = 29
5^2 + 4^2 = 41
5^2 + 6^2 = 61
5^2 + 8^2 = 89

The sums are all prime numbers. Then I idly calculated the reciprocal of 1/89:

1/89 = 0·011235955056179775...

The digits 011235… are the start of the Fibonacci sequence. It seems to go awry after that, but I remembered what David Wells had said in his wonderful Penguin Dictionary of Curious and Interesting Numbers (1986): “89 is the 11th Fibonacci number, and the period of its reciprocal is generated by the Fibonacci sequence: 1/89 = 0·11235…” He means that the Fibonacci sequence generates the digits of 1/89 like this, when you sum the columns and move carries left as necessary:

0
↓1
↓↓1
↓↓↓2
↓↓↓↓3
↓↓↓↓↓5
↓↓↓↓↓↓8
↓↓↓↓↓↓13
↓↓↓↓↓↓↓21
↓↓↓↓↓↓↓↓34
↓↓↓↓↓↓↓↓↓55
↓↓↓↓↓↓↓↓↓↓89...
↓↓↓↓↓↓↓↓↓↓
0112359550...

I tried this method of summing the Fibonacci sequence in other bases. Although it was old, the scientific calculator was crudely programmable. And it helpfully converted the sum into a final fraction once there were enough decimal digits:

0/3 + 1/32 + 1/33 + 2/34 + 3/35 + 5/36 + 8/37 + 13/38 + 21/39 + 34/310 + 55/311 + 89/312 + 144/313 + 233/314 + 377/315 + 610/316 + 987/317 + 1597/318 + 2584/319 + 4181/320 +... = 1/5 = 0·012101210121012101210 in b3

0/4 + 1/42 + 1/43 + 2/44 + 3/45 + 5/46 + 8/47 + 13/48 + 21/49 + 34/410 + 55/411 + 89/412 + 144/413 + 233/414 + 377/415 + 610/416 + 987/417 + 1597/418 + 2584/419 + 4181/420 +... = 1/11 = 0·011310113101131011310 in b4

0/5 + 1/52 + 1/53 + 2/54 + 3/55 + 5/56 + 8/57 + 13/58 + 21/59 + 34/510 + 55/511 + 89/512 + 144/513 + 233/514 + 377/515 + 610/516 + 987/517 + 1597/518 + 2584/519 + 4181/520 +... = 1/19 = 0·011242141011242141011 in b5

0/6 + 1/62 + 1/63 + 2/64 + 3/65 + 5/66 + 8/67 + 13/68 + 21/69 + 34/610 + 55/611 + 89/612 + 144/613 + 233/614 + 377/615 + 610/616 + 987/617 + 1597/618 + 2584/619 + 4181/620 +... = 1/29 = 0·011240454431510112404 in b6

0/7 + 1/72 + 1/73 + 2/74 + 3/75 + 5/76 + 8/77 + 13/78 + 21/79 + 34/710 + 55/711 + 89/712 + 144/713 + 233/714 + 377/715 + 610/716 + 987/717 + 1597/718 + 2584/719 + 4181/720 +... = 1/41 = 0·011236326213520225056 in b7

It was interesting to see that all the reciprocals so far were of primes. I carried on:

0/8 + 1/82 + 1/83 + 2/84 + 3/85 + 5/86 + 8/87 + 13/88 + 21/89 + 34/810 + 55/811 + 89/812 + 144/813 + 233/814 + 377/815 + 610/816 + 987/817 + 1597/818 + 2584/819 + 4181/820 +... = 1/55 = 0·011236202247440451710 in b8

Not a prime reciprocal, but a reciprocal of a Fibonacci number. Here are some more sums:

0/9 + 1/92 + 1/93 + 2/94 + 3/95 + 5/96 + 8/97 + 13/98 + 21/99 + 34/910 + 55/911 + 89/912 + 144/913 + 233/914 + 377/915 + 610/916 + 987/917 + 1597/918 + 2584/919 + 4181/920 +... = 1/71 (another prime) = 0·011236067540450563033 in b9

0/10 + 1/102 + 1/103 + 2/104 + 3/105 + 5/106 + 8/107 + 13/108 + 21/109 + 34/1010 + 55/1011 + 89/1012 + 144/1013 + 233/1014 + 377/1015 + 610/1016 + 987/1017 + 1597/1018 + 2584/1019 + 4181/1020 +... = 1/89 (and another) = 0·011235955056179775280 in b10

0/11 + 1/112 + 1/113 + 2/114 + 3/115 + 5/116 + 8/117 + 13/118 + 21/119 + 34/1110 + 55/1111 + 89/1112 + 144/1113 + 233/1114 + 377/1115 + 610/1116 + 987/1117 + 1597/1118 + 2584/1119 + 4181/1120 +... = 1/109 (and another) = 0·011235942695392022470 in b11

0/12 + 1/122 + 1/123 + 2/124 + 3/125 + 5/126 + 8/127 + 13/128 + 21/129 + 34/1210 + 55/1211 + 89/1212 + 144/1213 + 233/1214 + 377/1215 + 610/1216 + 987/1217 + 1597/1218 + 2584/1219 + 4181/1220 +... = 1/131 (and another) = 0·011235930336A53909A87 in b12

0/13 + 1/132 + 1/133 + 2/134 + 3/135 + 5/136 + 8/137 + 13/138 + 21/139 + 34/1310 + 55/1311 + 89/1312 + 144/1313 + 233/1314 + 377/1315 + 610/1316 + 987/1317 + 1597/1318 + 2584/1319 + 4181/1320 +... = 1/155 (not a prime or a Fibonacci number) = 0·01123591ACAA861794044 in b13

The reciprocals go like this:

1/1, 1/5, 1/11, 1/19, 1/29, 1/41, 1/55, 1/71, 1/89, 1/109, 1/131, 1/155...

And it should be easy to see the rule that generates them:

5 = 1 + 4
11 = 5 + 6
19 = 11 + 8
29 = 19 + 10
41 = 29 + 12
55 = 41 + 14
71 = 55 + 16
89 = 17 + 18
109 = 89 + 20
131 = 109 + 22
155 = 131 + 24
[...]

But I don’t understand why the rule applies, let alone why the Fibonacci sequence generates these reciprocals in the first place.

Fylfy Fractals

by in Fractals, Geometry, Mathematics, Rep-Tiles, Squares, Triangles and tagged , , , , , , , , , , | Leave a comment

An equilateral triangle is a rep-tile, because it can be tiled completely with smaller copies of itself. Here it is as a rep-4 rep-tile, tiled with four smaller copies of itself:

Equilateral triangle as rep-4 rep-tile

If you divide and discard one of the sub-copies, then carry on dividing-and-discarding with the sub-copies and sub-sub-copies and sub-sub-sub-copies, you get the fractal seen below. Alas, it’s not a very attractive or interesting fractal:

Divide-and-discard fractal stage #1

Stage #2

Stage #3

Stage #4

Stage #5

Stage #6

Stage #7

Stage #8

Stage #9

Divide-and-discard fractal (animated)

You can create more attractive and interesting fractals by rotating the sub-triangles clockwise or anticlockwise. Here are some examples:

Now try dividing a square into four right triangles, then turning each of the four triangles into a divide-and-discard fractal. The resulting four-fractal shape is variously called a swastika, a gammadion, a cross cramponnée, a Hakenkreuz and a fylfot. I’m calling it a fylfy fractal:

Divide-and-discard fractals in the four triangles of a divided square stage #1

Fylfy fractal #2

Fylfy fractal #3

Fylfy fractal #4

Fylfy fractal #5

Fylfy fractal #6

Fylfy fractal #7

Fylfy fractal #8

Fylfy fractal (animated)

Finally, you can adjust the fylfy fractals so that each point in the square becomes the equivalent point in a circle:

Absolutely Sabulous

by in Fractals, Mathematics and tagged , , , , , , , , , | Leave a comment

The Hourglass Fractal (animated gif optimized at ezGIF)

Performativizing Paronomasticity

The title of this incendiary intervention is a paronomasia on the title of the dire Absolutely Fabulous. The adjective sabulous means “sandy; consisting of or abounding in sand; arenaceous” (OED).

Elsewhere Other-Accessible

• Hour Re-Re-Re-Re-Powered — more on the hourglass fractal
• Allus Pour, Horic — an earlier paronomasia for the fractal

Game of Throwns

by in Chaos Game, Fractals, Geometry, Mathematics, Squares, Triangles and tagged , , , , , , , , , , , , | Leave a comment

In “Scaffscapes”, I looked at these three fractals and described how they were in a sense the same fractal, even though they looked very different:

Fractal #1

Fractal #2

Fractal #3

But even if they are all the same in some mathematical sense, their different appearances matter in an aesthetic sense. Fractal #1 is unattractive and seems uninteresting:

Fractal #1, unattractive, uninteresting and unnamed

Fractal #3 is attractive and interesting. That’s part of why mathematicians have given it a name, the T-square fractal:

Fractal #3 — the T-square fractal

But fractal #2, although it’s attractive and interesting, doesn’t have a name. It reminds me of a ninja throwing-star or shuriken, so I’ve decided to call it the throwing-star fractal or ninja-star fractal:

Fractal #2, the throwing-star fractal

A ninja throwing-star or shuriken

This is one way to construct a throwing-star fractal:

Throwing-star fractal, stage 1

Throwing-star fractal, #2

Throwing-star fractal, #3

Throwing-star fractal, #4

Throwing-star fractal, #5

Throwing-star fractal, #6

Throwing-star fractal, #7

Throwing-star fractal, #8

Throwing-star fractal, #9

Throwing-star fractal, #10

Throwing-star fractal, #11

Throwing-star fractal (animated)

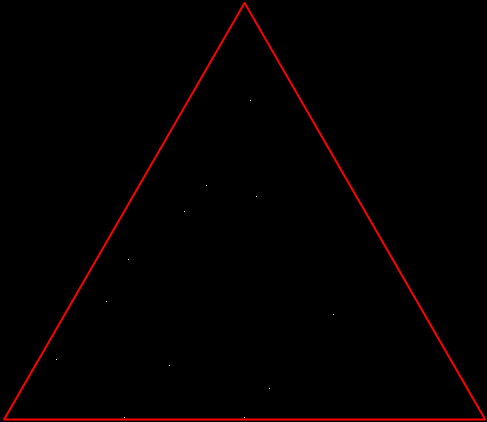
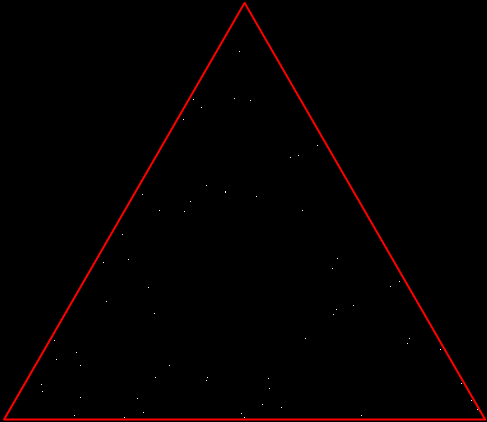
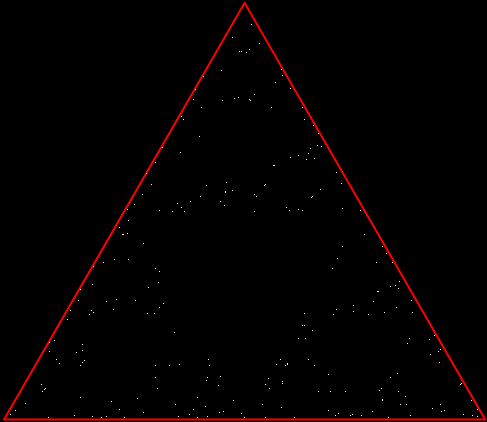
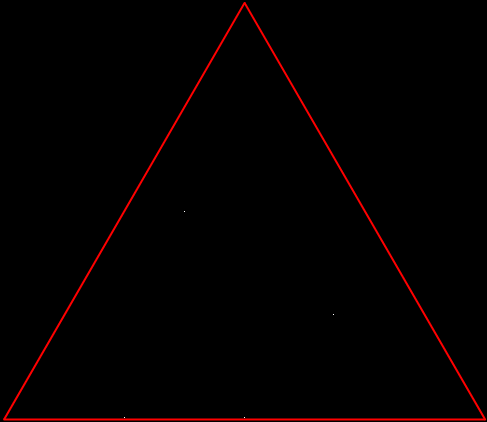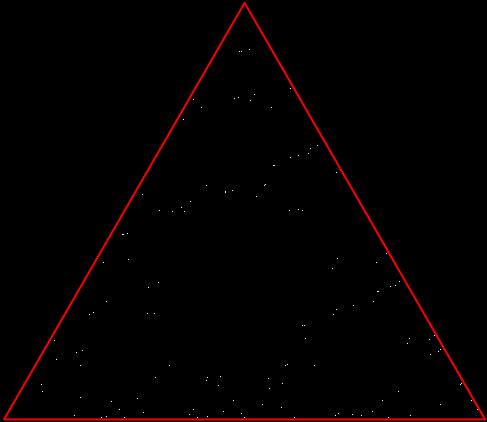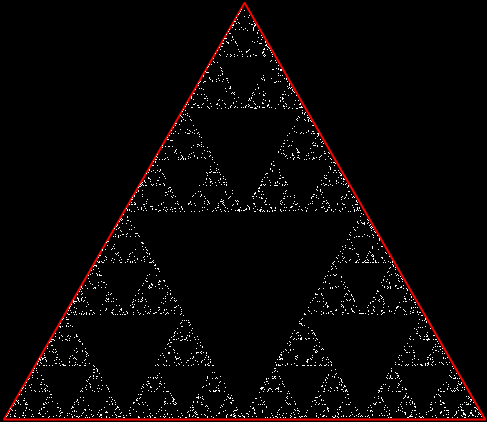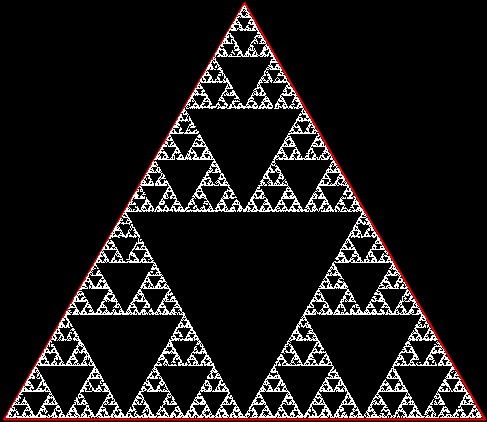
But there’s another way to construct a throwing-star fractal. You use what’s called the chaos game. To understand the commonest form of the chaos game, imagine a ninja inside an equilateral triangle throwing a shuriken again and again halfway towards a randomly chosen vertex of the triangle. If you mark each point where the shuriken lands, you eventually get a fractal called the Sierpiński triangle:

Chaos game with triangle stage 1

Chaos triangle #2

Chaos triangle #3

Chaos triangle #4

Chaos triangle #5

Chaos triangle #6

Chaos triangle #7

Chaos triangle (animated)

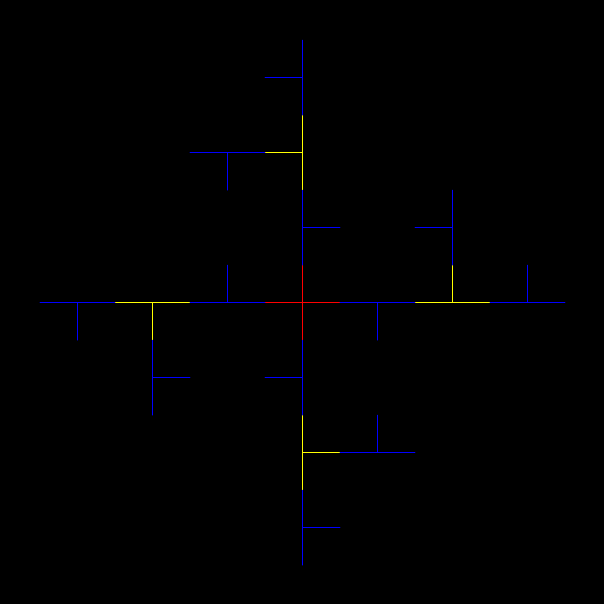
When you try the chaos game with a square, with the ninja throwing the shuriken again and again halfway towards a randomly chosen vertex, you don’t get a fractal. The interior of the square just fills more or less evenly with points:

Chaos game with square, stage 1

Chaos square #2

Chaos square #3

Chaos square #4

Chaos square #5

Chaos square #6

Chaos square (anim)

But suppose you restrict the ninja’s throws in some way. If he can’t throw twice or more in a row towards the same vertex, you get a familiar fractal:

Chaos game with square, ban on throwing towards same vertex, stage 1

Chaos square, ban = v+0, #2

Chaos square, ban = v+0, #3

Chaos square, ban = v+0, #4

Chaos square, ban = v+0, #5

Chaos square, ban = v+0, #6

Chaos square, ban = v+0 (anim)

But what if the ninja can’t throw the shuriken towards the vertex one place anti-clockwise of the vertex he’s just thrown it towards? Then you get another familiar fractal — the throwing-star fractal:

Chaos square, ban = v+1, stage 1

Chaos square, ban = v+1, #2

Chaos square, ban = v+1, #3

Chaos square, ban = v+1, #4

Chaos square, ban = v+1, #5

Game of Throwns — throwing-star fractal from chaos game (static)

Game of Throwns — throwing-star fractal from chaos game (anim)

And what if the ninja can’t throw towards the vertex two places anti-clockwise (or two places clockwise) of the vertex he’s just thrown the shuriken towards? Then you get a third familiar fractal — the T-square fractal:

Chaos square, ban = v+2, stage 1

Chaos square, ban = v+2, #2

Chaos square, ban = v+2, #3

Chaos square, ban = v+2, #4

Chaos square, ban = v+2, #5

T-square fractal from chaos game (static)

T-square fractal from chaos game (anim)

Finally, what if the ninja can’t throw towards the vertex three places anti-clockwise, or one place clockwise, of the vertex he’s just thrown the shuriken towards? If you can guess what happens, your mathematical intuition is much better than mine.

Post-Performative Post-Scriptum

I am not now and never have been a fan of George R.R. Martin. He may be a good author but I’ve always suspected otherwise, so I’ve never read any of his books or seen any of the TV adaptations.