Monthly Archives: March 2021

Root Routes

by in Chaos Game, Fractals, Geometry, Mathematics, Square Roots, Squares, Triangles and tagged , , , , , , , , , , , , , , | Leave a comment

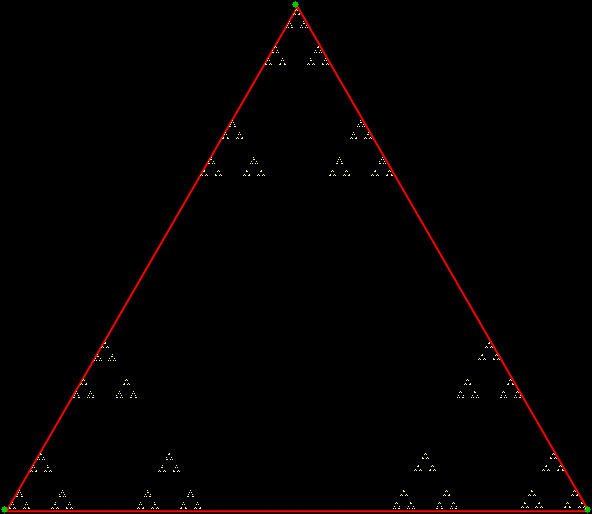
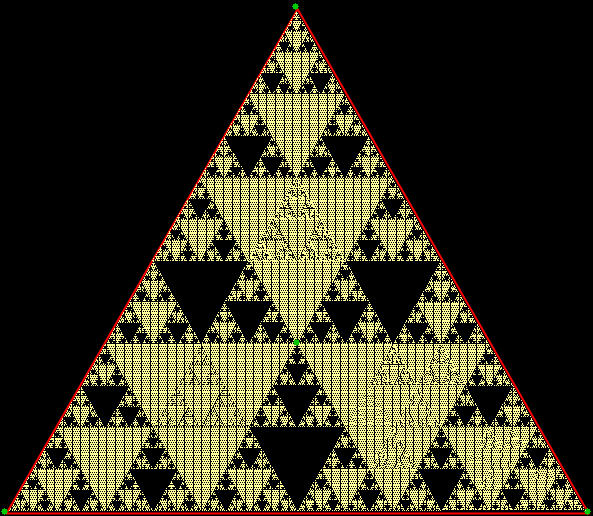
Suppose a point traces all possible routes jumping half-way towards the three vertices of an equilateral triangle. A special kind of shape appears — a fractal called the Sierpiński triangle that contains copies of itself at smaller and smaller scales:

Sierpiński triangle, jump = 1/2

And what if the point jumps 2/3rds of the way towards the vertices as it traces all possible routes? You get this dull fractal:

Triangle, jump = 2/3

But if you add targets midway along each side of the triangle, you get this fractal with the 2/3rds jump:

Triangle, jump = 2/3, side-targets

Now try the 1/2-jump triangle with a target at the center of the triangle:

Triangle, jump = 1/2, central target

And the 2/3-jump triangle with side-targets and a central target:

Triangle, jump = 2/3, side-targets, central target

But why stop at simple jumps like 1/2 and 2/3? Let’s take the distance to the target, td, and use the function 1-(sqrt(td/7r)), where sqrt() is the square-root and 7r is 7 times the radius of the circumscribing circle:

Triangle, jump = 1-(sqrt(td/7r))

Here’s the same jump with a central target:

Triangle, jump = 1-(sqrt(td/7r)), central target

Now let’s try squares with various kinds of jump. A square with a 1/2-jump fills evenly with points:

Square, jump = 1/2 (animated)

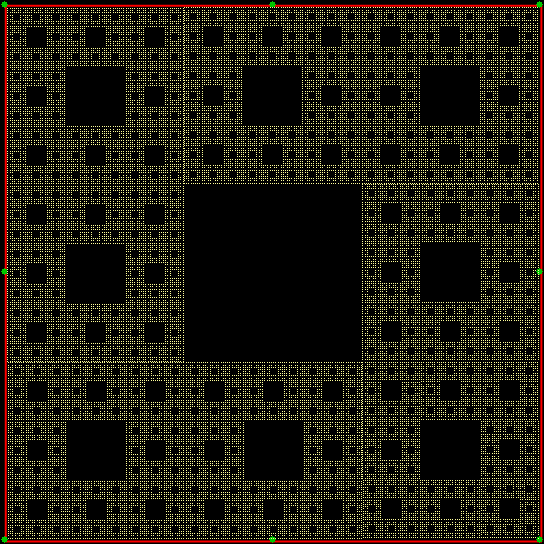
The 2/3-jump does better with a central target:

Square, jump = 2/3, central target

Or with side-targets:

Square, jump = 2/3, side-targets

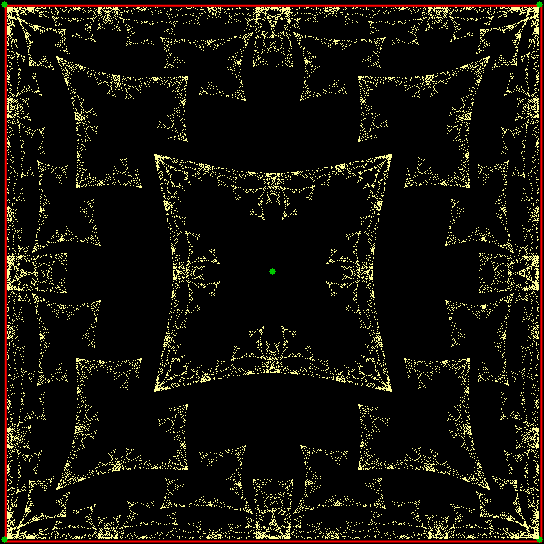
Now try some more complicated jumps:

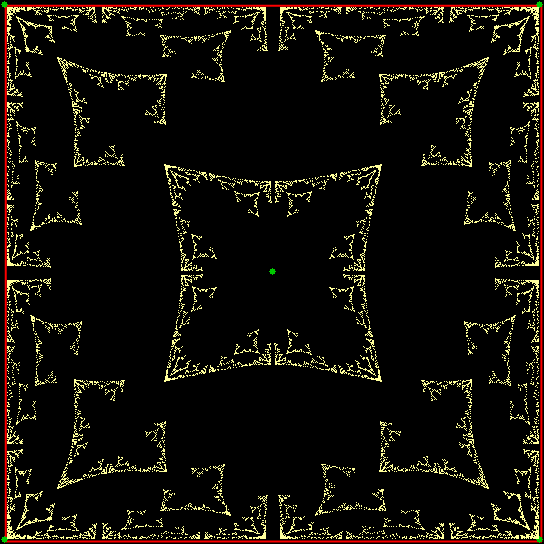
Square, jump = 1-sqrt(td/7r)

Square, jump = 1-sqrt(td/15r), side-targets

And what if you ban the point from jumping twice or more towards the same target? You get this fractal:

Square, jump = 1-sqrt(td/6r), ban = prev+0

Now try a ban on jumping towards the target two places clockwise of the previous target:

Square, jump = 1-sqrt(td/6r), ban = prev+2

And the two-place ban with a central target:

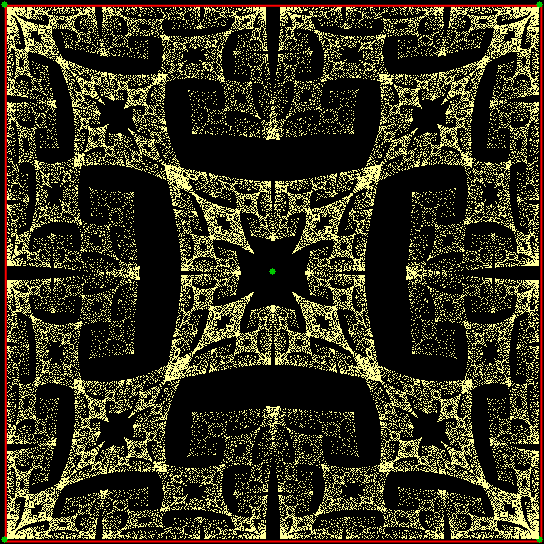
Square, jump = 1-sqrt(td/6r), ban = prev+2, central target

And so on:

Square, jump = 1-sqrt(td/6.93r), ban = prev+2, central target

Square, jump = 1-sqrt(td/7r), ban = prev+2, central target

These fractals take account of the previous jump and the pre-previous jump:

Square, jump = 1-sqrt(td/4r), ban = prev+2,2, central target

Square, jump = 1-sqrt(td/5r), ban = prev+2,2, central target

Square, jump = 1-sqrt(td/6r), ban = prev+2,2, central target

Elsewhere other-accessible

• Boole(b)an #2 — fractals created in similar ways

Oh My Guardian #9

by in 2SLGBTQ+ Community Issues, Guardianistas, Politics, Quotations and tagged , , , , , , , , , , , , , , , , , , , | Leave a comment

Cultural gayness has a fraught history in pop culture. Ever since Aids began to pick off members of the queer cultural elite in the 80s, femininity and queer signifiers (ahem, like glitter) became red flags for disease and moral corruption. The tabloid media systematically crucified gay people, using these feminine signifiers as tracking beacons. Closeting oneself and cloaking one’s femininity became a matter of survival, and not just for celebrities. — Claiming Shawn Mendes is queer is an own goal for gay men, Brian O’Flynn, The Guardian, 28xi2018.

This Charming Dis-Arming

by in Chaos Game, Fractals, Geometry, Mathematics, Squares, Triangles and tagged , , , , , , , , , , , , , , , , , , | Leave a comment

One of the charms of living in an old town or city is finding new routes to familiar places. It’s also one of the charms of maths. Suppose a three-armed star sprouts three half-sized arms from the end of each of its three arms. And then sprouts three quarter-sized arms from the end of each of its nine new arms. And so on. This is what happens:

Three-armed star

3-Star sprouts more arms

Sprouting 3-Star #3

Sprouting 3-Star #4

Sprouting 3-Star #5

Sprouting 3-Star #6

Sprouting 3-Star #7

Sprouting 3-Star #8

Sprouting 3-Star #9

Sprouting 3-Star #10

Sprouting 3-Star #11 — the Sierpiński triangle

Sprouting 3-star (animated)

The final stage is a famous fractal called the Sierpiński triangle — the sprouting 3-star is a new route to a familiar place. But what happens when you trying sprouting a four-armed star in the same way? This does:

Four-armed star #1

Sprouting 4-Star #2

Sprouting 4-Star #3

Sprouting 4-Star #4

Sprouting 4-Star #5

Sprouting 4-Star #6

Sprouting 4-Star #7

Sprouting 4-Star #8

Sprouting 4-Star #9

Sprouting 4-Star #10

Sprouting 4-star (animated)

There’s no obvious fractal with a sprouting 4-star. Not unless you dis-arm the 4-star in some way. For example, you can ban any new arm sprouting in the same direction as the previous arm:

Dis-armed 4-star (+0) #1

Dis-armed 4-Star (+0) #2

Dis-armed 4-Star (+0) #3

Dis-armed 4-Star (+0) #4

Dis-armed 4-Star (+0) #5

Dis-armed 4-Star (+0) #6

Dis-armed 4-Star (+0) #7

Dis-armed 4-Star (+0) #8

Dis-armed 4-Star (+0) #9

Dis-armed 4-Star (+0) #10

Dis-armed 4-star (+0) (animated)

Once again, it’s a new route to a familiar place (for keyly committed core components of the Overlord-of-the-Über-Feral community, anyway). Now try banning an arm sprouting one place clockwise of the previous arm:

Dis-armed 4-Star (+1) #1

Dis-armed 4-Star (+1) #2

Dis-armed 4-Star (+1) #3

Dis-armed 4-Star (+1) #4

Dis-armed 4-Star (+1) #5

Dis-armed 4-Star (+1) #6

Dis-armed 4-Star (+1) #7

Dis-armed 4-Star (+1) #8

Dis-armed 4-Star (+1) #9

Dis-armed 4-Star (+1) #10

Dis-armed 4-Star (+1) (animated)

Again it’s a new route to a familiar place. Now trying banning an arm sprouting two places clockwise (or anti-clockwise) of the previous arm:

Dis-armed 4-Star (+2) #1

Dis-armed 4-Star (+2) #2

Dis-armed 4-Star (+2) #3

Dis-armed 4-Star (+2) #4

Dis-armed 4-Star (+2) #5

Dis-armed 4-Star (+2) #6

Dis-armed 4-Star (+2) #7

Dis-armed 4-Star (+2) #8

Dis-armed 4-Star (+2) #9

Dis-armed 4-Star (+2) #10

Dis-armed 4-Star (+2) (animated)

Once again it’s a new route to a familiar place. And what happens if you ban an arm sprouting three places clockwise (or one place anti-clockwise) of the previous arm? You get a mirror image of the Dis-armed 4-Star (+1):

Dis-armed 4-Star (+3)

Here’s the Dis-armed 4-Star (+1) for comparison:

Dis-armed 4-Star (+1)

Elsewhere other-accessible

• Boole(b)an #2 — other routes to the fractals seen above

Freeze Please Me

by in Art, Language, Music, Quotations, Translation and tagged , , , , , , , , , , , , | Leave a comment

“Ich habe unter meinen Papieren ein Blatt gefunden,” sagte Goethe, “wo ich die Baukunst eine erstarrte Musik nenne.” — Gespräche mit Goethe, Johann Peter Eckermann (1836)

• “I have found a sheet among my papers,” said Goethe, “where I call architecture a frozen music.” — Conversations with Goethe

N.B. The aphorism “Architecture is frozen music” has also sometimes been attributed to Friedrich von Schelling (1775-1854) and Ganopati Sthapat (1927-2011).

Peri-Performative Post-Scriptum

The toxic title of this paronomastic post is a key reference to core Beatles album Please Please Me (1963).